Порог перколяции
| Часть серии о | ||||
| Сетевая наука | ||||
|---|---|---|---|---|
| Типы сетей | ||||
| Графики | ||||
|
||||
| Модели | ||||
|
||||
| ||||
Эта статья может быть слишком технической для понимания большинства читателей . ( Март 2021 г. ) |
Порог перколяции — математическое понятие в теории перколяции , которое описывает формирование дальней связности в случайных системах. Ниже порога гигантской компоненты связности не существует; а над ним существует гигантская компонента порядка размера системы. В технике и приготовлении кофе перколяция представляет собой поток жидкостей через пористую среду , но в мире математики и физики она обычно относится к упрощенным решетчатым моделям случайных систем или сетей ( графов ) и природе связности в них. Порог перколяции — это критическое значение вероятности заполнения p или, в более общем смысле, критическая поверхность для группы параметров p 1 , p 2 бесконечная связность ( перколяция ). , ..., такая, что сначала возникает [ 1 ]
Модели перколяции
[ редактировать ]Наиболее распространенная модель перколяции состоит в том, чтобы взять регулярную решетку, например квадратную, и превратить ее в случайную сеть путем случайного «занятия» узлов (вершин) или связей (ребер) со статистически независимой вероятностью p . При критическом пороге pc порогом сначала появляются большие кластеры и дальняя связность, и это называется перколяции . В зависимости от метода получения случайной сети различают порог перколяции сайтов и порог перколяции связей . Более общие системы имеют несколько вероятностей p 1 , p 2 и т. д., а переход характеризуется критической поверхностью или многообразием . Можно также рассмотреть системы континуума, такие как перекрывающиеся диски и сферы, расположенные случайным образом, или отрицательное пространство ( швейцарского сыра модели ).
Чтобы понять порог, вы можете рассмотреть такую величину, как вероятность того, что существует непрерывный путь от одной границы к другой вдоль занятых сайтов или связей, то есть внутри одного кластера. Например, можно рассмотреть квадратную систему и задать вероятность P того, что существует путь от верхней границы до нижней границы. В зависимости от вероятности занятия p можно найти сигмоидальный график, который идет от P=0 при p=0 до P=1 при p=1 . Чем больше квадрат по сравнению с шагом решетки, тем резче будет переход. размер системы стремится к бесконечности, P(p) будет ступенчатой функцией при пороговом значении pc Когда . Для конечных больших систем P( pc ) — константа, значение которой зависит от формы системы; для квадратной системы, обсуждавшейся выше, P(p c )= 1 ⁄ 2 ровно для любой решетки по простому аргументу симметрии.
Есть и другие признаки критического порога. Например, распределение по размерам (количество кластеров размером s ) спадает по степенному закону для больших s на пороге, ns . ( pc ) ~ s -т зависящие от размерности , где τ — критические показатели перколяции, . Для бесконечной системы критический порог соответствует первой точке (при увеличении p ), где размер кластеров становится бесконечным.
В описанных до сих пор системах предполагалось, что заселение узла или связи совершенно случайно — это так называемая Бернулли перколяция . Для непрерывной системы случайное заселение соответствует точкам, размещаемым с помощью процесса Пуассона . Дальнейшие вариации включают коррелированную перколяцию, например, перколяционные кластеры, связанные с моделями ферромагнетиков Изинга и Поттса, в которых связи записываются методом Фортюина- Кастелейна . [ 2 ] При начальной загрузке или перколяции k-sat сайты и/или связи сначала заполняются, а затем последовательно удаляются из системы, если сайт не имеет хотя бы k соседей. Другая важная модель перколяции, относящаяся к другому классу универсальности вообще , — это направленная перколяция , где связность вдоль связи зависит от направления потока.
За последние несколько десятилетий была проделана огромная работа по нахождению точных и приблизительных значений порогов перколяции для множества таких систем. Точные пороги известны только для некоторых двумерных решеток, которые можно разбить на самодвойственный массив, так что при преобразовании треугольник-треугольник система остается той же самой. Исследования с использованием численных методов привели к многочисленным улучшениям алгоритмов и нескольким теоретическим открытиям.
Простая двойственность в двух измерениях подразумевает, что все полностью триангулированные решетки (например, треугольная решетка, решетка Юнион Джека, перекрестная двойная, двойная по мартини и асаноха или двойственная 3-12, а также триангуляция Делоне) имеют пороговые значения узлов 1 ⁄ 2 , а самодуальные решетки (квадратные, мартини-B) имеют пороги связи 1 ⁄ 2 .
Обозначения типа (4,8 2 ) родом из Грюнбаума и Шепарда , [ 3 ] и указывает, что вокруг данной вершины, двигаясь по часовой стрелке, встречается сначала квадрат, а затем два восьмиугольника. Помимо одиннадцати архимедовых решеток, составленных из правильных многоугольников, каждый узел которых эквивалентен, было изучено множество других, более сложных решеток с узлами разных классов.
Столбики ошибок в последней цифре или цифрах показаны числами в скобках. Таким образом, 0,729724(3) означает 0,729724 ± 0,000003, а 0,74042195(80) означает 0,74042195 ± 0,00000080. Столбики погрешностей по-разному представляют одно или два стандартных отклонения чистой ошибки (включая статистическую и ожидаемую систематическую ошибку) или эмпирический доверительный интервал, в зависимости от источника.
Проникновение в сети
[ редактировать ]Для случайной древовидной сети (т. е. связной сети без цикла) без степени корреляции можно показать, что такая сеть может иметь гигантскую компоненту , а порог перколяции (вероятность передачи) определяется выражением
.
Где – производящая функция, соответствующая распределению избыточных степеней , - средняя степень сети и – второй момент распределения степеней . Так, например, для сети ER , поскольку распределение степеней является распределением Пуассона , порог находится на уровне .
В сетях с кластеризацией низкой , критическая точка масштабируется на такой, что: [ 4 ]
Это указывает на то, что для данного распределения степеней кластеризация приводит к большему порогу перколяции, главным образом потому, что для фиксированного числа связей структура кластеризации усиливает ядро сети ценой размывания глобальных связей. Для сетей с высокой степенью кластеризации сильная кластеризация может вызвать структуру ядро-периферия, в которой ядро и периферия могут находиться в разных критических точках, и приведенная выше приблизительная трактовка неприменима. [ 5 ]
Перколяция в 2D
[ редактировать ]Пороги на архимедовых решетках
[ редактировать ]
| Решетка | С | Порог проникновения сайта | Порог перколяции облигаций | |
|---|---|---|---|---|
| 3-12 или супер-кагоме (3, 12 2 ) | 3 | 3 | 0,807900764... = (1 − 2 sin ( π /18)) 1 ⁄ 2 [ 7 ] | 0.74042195(80), [ 8 ] 0.74042077(2), [ 9 ] 0.740420800(2), [ 10 ] 0.7404207988509(8), [ 11 ] [ 12 ] 0.740420798850811610(2), [ 13 ] |
| крест, усеченный тришестиугольник (4, 6, 12) | 3 | 3 | 0.746, [ 14 ] 0.750, [ 15 ] 0.747806(4), [ 7 ] 0.7478008(2) [ 11 ] | 0.6937314(1), [ 11 ] 0.69373383(72), [ 8 ] 0.693733124922(2) [ 13 ] |
| квадратный восьмиугольник, плитка для ванной, 4-8, усеченный квадрат
(4, 8 2 ) |
3 | - | 0.729, [ 14 ] 0.729724(3), [ 7 ] 0.7297232(5) [ 11 ] | 0.6768, [ 16 ] 0.67680232(63), [ 8 ] 0.6768031269(6), [ 11 ] 0.6768031243900113(3), [ 13 ] |
| соты (6 3 ) | 3 | 3 | 0.6962(6), [ 17 ] 0.697040230(5), [ 11 ] 0.6970402(1), [ 18 ] 0.6970413(10), [ 19 ] 0.697043(3), [ 7 ] | 0,652703645... = 1-2 грех (π/18), 1+ р 3 -3-3р 2 =0 [ 20 ] |
| кагоме (3, 6, 3, 6) | 4 | 4 | 0,652703645... = 1 - 2 sin( π /18) [ 20 ] | 0.5244053(3), [ 21 ] 0.52440516(10), [ 19 ] 0.52440499(2), [ 18 ] 0.524404978(5), [ 9 ] 0.52440572..., [ 22 ] 0.52440500(1), [ 10 ] 0.524404999173(3), [ 11 ] [ 12 ] 0.524404999167439(4) [ 23 ] 0.52440499916744820(1) [ 13 ] |
| рубин, [ 24 ] ромбитришестиугольные (3, 4, 6, 4) | 4 | 4 | 0.620, [ 14 ] 0.621819(3), [ 7 ] 0.62181207(7) [ 11 ] | 0.52483258(53), [ 8 ] 0.5248311(1), [ 11 ] 0.524831461573(1) [ 13 ] |
| квадрат (4 4 ) | 4 | 4 | 0.59274(10), [ 25 ] 0.59274605079210(2), [ 23 ] 0.59274601(2), [ 11 ] 0.59274605095(15), [ 26 ] 0.59274621(13), [ 27 ] 0.592746050786(3), [ 28 ] 0.59274621(33), [ 29 ] 0.59274598(4), [ 30 ] [ 31 ] 0.59274605(3), [ 18 ] 0.593(1), [ 32 ] 0.591(1), [ 33 ] 0.569(13), [ 34 ] 0.59274(5) [ 35 ] | 1 ⁄ 2 |
| курносый шестиугольный , кленовый лист [ 36 ] (3 4 ,6) | 5 | 5 | 0.579 [ 15 ] 0.579498(3) [ 7 ] | 0.43430621(50), [ 8 ] 0.43432764(3), [ 11 ] 0.4343283172240(6), [ 13 ] |
| курносый квадрат , пазл (3 2 , 4, 3, 4 ) | 5 | 5 | 0.550, [ 14 ] [ 37 ] 0.550806(3) [ 7 ] | 0.41413743(46), [ 8 ] 0.4141378476(7), [ 11 ] 0.4141378565917(1), [ 13 ] |
| фриз, вытянутый треугольный (3 3 , 4 2 ) | 5 | 5 | 0.549, [ 14 ] 0.550213(3), [ 7 ] 0.5502(8) [ 38 ] | 0.4196(6), [ 38 ] 0.41964191(43), [ 8 ] 0.41964044(1), [ 11 ] 0.41964035886369(2) [ 13 ] |
| треугольный (3 6 ) | 6 | 6 | 1 ⁄ 2 | 0,347296355... = 2 sin ( π /18), 1 + p 3 − 3 р = 0 [ 20 ] |
Примечание: иногда вместо сот используется слово «шестиугольная», хотя в некоторых контекстах треугольную решетку также называют шестиугольной решеткой . z = объемное координационное число .
2D-решетки с расширенными и сложными окрестностями
[ редактировать ]В этом разделе sq-1,2,3 соответствует квадрату (NN+2NN+3NN), [ 39 ] и т. д. Эквивалентно квадрату-2N+3N+4N, [ 40 ] кв(1,2,3). [ 41 ] tri = треугольный, hc = соты.
| Решетка | С | Порог проникновения сайта | Порог перколяции облигаций |
|---|---|---|---|
| кв-1, кв-2, кв-3, кв-5 | 4 | 0.5927... [ 39 ] [ 40 ] (квадратный участок) | |
| кв-1,2, кв-2,3, кв-3,5 | 8 | 0.407... [ 39 ] [ 40 ] [ 42 ] (квадратное соответствие) | 0.25036834(6), [ 18 ] 0.2503685, [ 43 ] 0.25036840(4) [ 44 ] |
| кв-1,3 | 8 | 0.337 [ 39 ] [ 40 ] | 0.2214995 [ 43 ] |
| кв-2,5: 2НН+5НН | 8 | 0.337 [ 40 ] | |
| hc-1,2,3: соты-NN+2NN+3NN | 12 | 0.300, [ 41 ] 0.300, [ 15 ] 0,302960... = 1-п с (узел, гк) [ 45 ] | |
| три-1,2: треугольный-NN+2NN | 12 | 0.295, [ 41 ] 0.289, [ 15 ] 0.290258(19) [ 46 ] | |
| три-2,3: треугольный-2NN+3NN | 12 | 0.232020(36), [ 47 ] 0.232020(20) [ 46 ] | |
| кв-4: квадрат-4NN | 8 | 0.270... [ 40 ] | |
| sq-1,5: квадрат-NN+5NN (r ≤ 2) | 8 | 0.277 [ 40 ] | |
| sq-1,2,3: квадрат-NN+2NN+3NN | 12 | 0.292, [ 48 ] 0.290(5) [ 49 ] 0.289, [ 15 ] 0.288, [ 39 ] [ 40 ] | 0.1522203 [ 43 ] |
| кв-2,3,5: квадрат-2НН+3НН+5НН | 12 | 0.288 [ 40 ] | |
| кв-1,4: квадрат-NN+4NN | 12 | 0.236 [ 40 ] | |
| кв-2,4: квадрат-2НН+4НН | 12 | 0.225 [ 40 ] | |
| три-4: треугольный-4NN | 12 | 0.192450(36), [ 47 ] 0.1924428(50) [ 46 ] | |
| hc-2,4: соты-2NN+4NN | 12 | 0.2374 [ 50 ] | |
| три-1,3: треугольный-NN+3NN | 12 | 0.264539(21) [ 46 ] | |
| три-1,2,3: треугольный-NN+2NN+3NN | 18 | 0.225, [ 48 ] 0.215, [ 15 ] 0.215459(36) [ 47 ] 0.2154657(17) [ 46 ] | |
| кв-3,4: 3НН+4НН | 12 | 0.221 [ 40 ] | |
| кв-1,2,5: NN+2NN+5NN | 12 | 0.240 [ 40 ] | 0.13805374 [ 43 ] |
| sq-1,3,5: NN+3NN+5NN | 12 | 0.233 [ 40 ] | |
| кв-4,5: 4НН+5НН | 12 | 0.199 [ 40 ] | |
| sq-1,2,4: NN+2NN+4NN | 16 | 0.219 [ 40 ] | |
| sq-1,3,4: NN+3NN+4NN | 16 | 0.208 [ 40 ] | |
| кв-2,3,4: 2NN+3NN+4NN | 16 | 0.202 [ 40 ] | |
| sq-1,4,5: NN+4NN+5NN | 16 | 0.187 [ 40 ] | |
| кв-2,4,5: 2НН+4НН+5НН | 16 | 0.182 [ 40 ] | |
| кв-3,4,5: 3НН+4НН+5НН | 16 | 0.179 [ 40 ] | |
| sq-1,2,3,5: NN+2NN+3NN+5NN | 16 | 0.208 [ 40 ] | 0.1032177 [ 43 ] |
| три-4,5: 4НН+5НН | 18 | 0.140250(36), [ 47 ] | |
| sq-1,2,3,4: NN+2NN+3NN+4NN ( ) | 20 | 0.19671(9), [ 51 ] 0.196, [ 40 ] 0.196724(10) [ 52 ] | 0.0841509 [ 43 ] |
| sq-1,2,4,5: NN+2NN+4NN+5NN | 20 | 0.177 [ 40 ] | |
| sq-1,3,4,5: NN+3NN+4NN+5NN | 20 | 0.172 [ 40 ] | |
| кв-2,3,4,5: 2НН+3НН+4НН+5НН | 20 | 0.167 [ 40 ] | |
| sq-1,2,3,5,6: NN+2NN+3NN+5NN+6NN | 20 | 0.0783110 [ 43 ] | |
| sq-1,2,3,4,5: NN+2NN+3NN+4NN+5NN ( ) | 24 | 0.164 [ 40 ] | |
| три-1,4,5: NN+4NN+5NN | 24 | 0.131660(36) [ 47 ] | |
| sq-1,...,6: NN+...+6NN (r≤3) | 28 | 0.142 [ 15 ] | 0.0558493 [ 43 ] |
| три-2,3,4,5: 2NN+3NN+4NN+5NN | 30 | 0.117460(36) [ 47 ] 0.135823(27) [ 46 ] | |
| три-1,2,3,4,5: NN+2NN+3NN+4NN+5NN |
36 | 0.115, [ 15 ] 0.115740(36), [ 47 ] 0.1157399(58) [ 46 ] | |
| sq-1,...,7: NN+...+7NN ( ) | 36 | 0.113 [ 15 ] | 0.04169608 [ 43 ] |
| квадрат: квадратное расстояние ≤ 4 | 40 | 0.105(5) [ 49 ] | |
| sq-(1,...,8: NN+..+8NN ( ) | 44 | 0.095, [ 37 ] 0.095765(5), [ 52 ] 0.09580(2) [ 51 ] | |
| sq-1,...,9: NN+..+9NN (r≤4) | 48 | 0.086 [ 15 ] | 0.02974268 [ 43 ] |
| sq-1,...,11: NN+...+11NN ( ) | 60 | 0.02301190(3) [ 43 ] | |
| кв-1,...,23 (r ≤ 7) | 148 | 0.008342595 [ 44 ] | |
| sq-1,...,32: NN+...+32NN ( ) | 224 | 0.0053050415(33) [ 43 ] | |
| sq-1,...,86: NN+...+86NN (r≤15) | 708 | 0.001557644(4) [ 53 ] | |
| sq-1,...,141: NN+...+141NN ( ) | 1224 | 0.000880188(90) [ 43 ] | |
| sq-1,...,185: NN+...+185NN (r≤23) | 1652 | 0.000645458(4) [ 53 ] | |
| sq-1,...,317: NN+...+317NN (r≤31) | 3000 | 0.000349601(3) [ 53 ] | |
| sq-1,...,413: NN+...+413NN ( ) | 4016 | 0.0002594722(11) [ 43 ] | |
| квадрат: квадратное расстояние ≤ 6 | 84 | 0.049(5) [ 49 ] | |
| квадрат: квадратное расстояние ≤ 8 | 144 | 0.028(5) [ 49 ] | |
| квадрат: квадратное расстояние ≤ 10 | 220 | 0.019(5) [ 49 ] | |
| 2х2 квадрата решетки* (также выше) | 20 | φ с = 0,58365(2), [ 52 ] р с = 0,196724(10), [ 52 ] 0.19671(9), [ 51 ] | |
| Решетчатые квадраты 3x3* (также выше) | 44 | φ с = 0,59586(2), [ 52 ] р с = 0,095765(5), [ 52 ] 0.09580(2) [ 51 ] | |
| Решетчатые квадраты 4х4* | 76 | φ с = 0,60648(1), [ 52 ] р с = 0,0566227(15), [ 52 ] 0.05665(3), [ 51 ] | |
| Решетчатые квадраты 5х5* | 116 | φ с = 0,61467(2), [ 52 ] р с = 0,037428(2), [ 52 ] 0.03745(2), [ 51 ] | |
| Решетчатые квадраты 6х6* | 220 | р с = 0,02663(1), [ 51 ] | |
| 10x10 квадратов решетки* | 436 | φ с = 0,36391(2), [ 52 ] р с = 0,0100576(5) [ 52 ] |
Здесь NN = ближайший сосед, 2NN = второй ближайший сосед (или следующий ближайший сосед), 3NN = третий ближайший сосед (или следующий ближайший сосед) и т. д. В некоторых статьях их также называют 2N, 3N, 4N соответственно. [ 39 ]
- Для перекрытия или соприкосновения квадратов, (сайт), приведенный здесь, представляет собой чистую долю занятых сайтов. похоже на в непрерывной перколяции. Случай квадрата 2×2 эквивалентен перколяции квадратной решетки NN+2NN+3NN+4NN или sq-1,2,3,4 с порогом с . [ 52 ] Квадрат 3×3 соответствует sq-1,2,3,4,5,6,7,8 с z =44 и . Значение z для квадрата k x k равно (2 k +1). 2 -5. О более крупных перекрывающихся квадратах см. [ 52 ]
2D искаженные решетки
[ редактировать ]Здесь искажается регулярная решетка с единичными интервалами, равномерно перемещая вершины внутри прямоугольника. и учитывает просачивание, когда сайты находятся в пределах евклидова расстояния друг друга.
| Решетка | Порог проникновения сайта | Порог перколяции облигаций | |||
|---|---|---|---|---|---|
| квадрат | 0.2 | 1.1 | 0.8025(2) [ 54 ] | ||
| 0.2 | 1.2 | 0.6667(5) [ 54 ] | |||
| 0.1 | 1.1 | 0.6619(1) [ 54 ] |
Перекрывающиеся фигуры на 2D-решетках
[ редактировать ]Порог узла — это количество перекрывающихся объектов на узел решетки. k — длина (чистая площадь). Перекрывающиеся квадраты показаны в разделе комплексной окрестности. Здесь z — координационное число k-меров любой ориентации, причем для палочки.
| Система | к | С | Покрытие сайта φ c | Порог проникновения сайта p c |
|---|---|---|---|---|
| Димер 1 х 2, квадратная решетка | 2 | 22 | 0.54691 [ 51 ]
0.5483(2) [ 55 ] |
0.17956(3) [ 51 ]
0.18019(9) [ 55 ] |
| 1 x 2 выровненных димера, квадратная решетка | 2 | 14 | 0.5715(18) [ 55 ] | 0.3454(13) [ 55 ] |
| Тример 1 х 3, квадратная решетка | 3 | 37 | 0.49898 [ 51 ]
0.50004(64) [ 55 ] |
0.10880(2) [ 51 ]
0.1093(2) [ 55 ] |
| Палочка 1 х 4, квадратная решетка | 4 | 54 | 0.45761 [ 51 ] | 0.07362(2) [ 51 ] |
| Палочка 1 х 5, квадратная решетка | 5 | 73 | 0.42241 [ 51 ] | 0.05341(1) [ 51 ] |
| Палочка 1 х 6, квадратная решетка | 6 | 94 | 0.39219 [ 51 ] | 0.04063(2) [ 51 ] |
Покрытие рассчитывается из к для палочки, потому что есть сайты, где палка приведет к перекрытию с данным сайтом.
Для выровненных палочки:
Приближенные формулы для порогов архимедовых решеток
[ редактировать ]| Решетка | С | Порог проникновения сайта | Порог перколяции облигаций |
|---|---|---|---|
| (3, 12 2 ) | 3 | ||
| (4, 6, 12) | 3 | ||
| (4, 8 2 ) | 3 | 0,676835..., 4 п 3 + 3 п. 4 − 6 п. 5 − 2 р 6 = 1 [ 56 ] | |
| соты (6 3 ) | 3 | ||
| кагоме (3, 6, 3, 6) | 4 | 0,524430..., 3 п 2 + 18:00 3 − 12 п. 4 + 6 п. 5 − п 6 = 1 [ 57 ] | |
| (3, 4, 6, 4) | 4 | ||
| квадрат (4 4 ) | 4 | 1 ⁄ 2 (точно) | |
| (3 4 ,6 ) | 5 | 0,434371..., 12 п 3 + 36 с. 4 − 21 п. 5 − 327 с. 6 + 69 с. 7 + 2532 р. 8 − 6533 р. 9 + 8256 р 10 − 6255 р. 11 + 2951 р 12 − 837 р. 13 + 126 с. 14 − 7 п. 15 = 1 [ нужна ссылка ] | |
| курносый квадрат, пазл (3 2 , 4, 3, 4 ) | 5 | ||
| (3 3 , 4 2 ) | 5 | ||
| треугольный (3 6 ) | 6 | 1 ⁄ 2 (точно) |
Перколяция AB и цветная перколяция в 2D
[ редактировать ]При перколяции AB - это доля сайтов A среди сайтов B, и связи возникают между сайтами противоположных видов. [ 58 ] Его еще называют антиперколяцией.
В цветной перколяции занятым местам присваивается один из цвета с равной вероятностью, а соединение осуществляется по связям между соседями разных цветов. [ 59 ]
| Решетка | С | Порог проникновения сайта | |
|---|---|---|---|
| треугольный AB | 6 | 6 | 0.2145, [ 58 ] 0.21524(34), [ 60 ] 0.21564(3) [ 61 ] |
| AB на квадратной накрывающей решетке | 6 | 6 | [ 62 ] |
| квадратный трехцветный | 4 | 4 | 0.80745(5) [ 59 ] |
| квадратный четырехцветный | 4 | 4 | 0.73415(4) [ 59 ] |
| квадратный пятицветный | 4 | 4 | 0.69864(7) [ 59 ] |
| квадратный шестицветный | 4 | 4 | 0.67751(5) [ 59 ] |
| треугольный двухцветный | 6 | 6 | 0.72890(4) [ 59 ] |
| треугольный трехцветный | 6 | 6 | 0.63005(4) [ 59 ] |
| треугольный четырехцветный | 6 | 6 | 0.59092(3) [ 59 ] |
| треугольный пятицветный | 6 | 6 | 0.56991(5) [ 59 ] |
| треугольный шестицветный | 6 | 6 | 0.55679(5) [ 59 ] |
Проникновение связей между сайтами в 2D
[ редактировать ]Проникновение связей на сайте. Здесь - вероятность занятия сайта и — это вероятность занятия связи, а связность осуществляется только в том случае, если и сайты, и связи на пути заняты. Условие критичности принимает вид кривой = 0 и некоторые конкретные критические пары перечислены ниже.
Квадратная решетка:
| Решетка | С | Порог проникновения сайта | Порог перколяции облигаций | |
|---|---|---|---|---|
| квадрат | 4 | 4 | 0.615185(15) [ 63 ] | 0.95 |
| 0.667280(15) [ 63 ] | 0.85 | |||
| 0.732100(15) [ 63 ] | 0.75 | |||
| 0.75 | 0.726195(15) [ 63 ] | |||
| 0.815560(15) [ 63 ] | 0.65 | |||
| 0.85 | 0.615810(30) [ 63 ] | |||
| 0.95 | 0.533620(15) [ 63 ] |
Сотовая (шестиугольная) решетка:
| Решетка | С | Порог проникновения сайта | Порог перколяции облигаций | |
|---|---|---|---|---|
| соты | 3 | 3 | 0.7275(5) [ 64 ] | 0.95 |
| 0. 0.7610(5) [ 64 ] | 0.90 | |||
| 0.7986(5) [ 64 ] | 0.85 | |||
| 0.80 | 0.8481(5) [ 64 ] | |||
| 0.8401(5) [ 64 ] | 0.80 | |||
| 0.85 | 0.7890(5) [ 64 ] | |||
| 0.90 | 0.7377(5) [ 64 ] | |||
| 0.95 | 0.6926(5) [ 64 ] |
Решетка Кагоме:
| Решетка | С | Порог проникновения сайта | Порог перколяции облигаций | |
|---|---|---|---|---|
| кагоме | 4 | 4 | 0.6711(4), [ 64 ] 0.67097(3) [ 65 ] | 0.95 |
| 0.6914(5), [ 64 ] 0.69210(2) [ 65 ] | 0.90 | |||
| 0.7162(5), [ 64 ] 0.71626(3) [ 65 ] | 0.85 | |||
| 0.7428(5), [ 64 ] 0.74339(3) [ 65 ] | 0.80 | |||
| 0.75 | 0.7894(9) [ 64 ] | |||
| 0.7757(8), [ 64 ] 0.77556(3) [ 65 ] | 0.75 | |||
| 0.80 | 0.7152(7) [ 64 ] | |||
| 0.81206(3) [ 65 ] | 0.70 | |||
| 0.85 | 0.6556(6) [ 64 ] | |||
| 0.85519(3) [ 65 ] | 0.65 | |||
| 0.90 | 0.6046(5) [ 64 ] | |||
| 0.90546(3) [ 65 ] | 0.60 | |||
| 0.95 | 0.5615(4) [ 64 ] | |||
| 0.96604(4) [ 65 ] | 0.55 | |||
| 0.9854(3) [ 65 ] | 0.53 |
* Значения для разных решеток см. в «Исследовании перколяции узловых связей на многих решетках». [ 64 ]
Приблизительная формула перколяции межсайтовых связей на сотовой решетке
| Решетка | С | Порог | Примечания | |
|---|---|---|---|---|
| (6 3 ) соты | 3 | 3 | , При равенстве: p s = p b = 0,82199 | приблизительная формула, p s = вероятность сайта, p b = вероятность связи, p bc = 1 - 2 sin ( π /18), [ 19 ] точно при p s =1, p b =p bc . |
Архимедовы двойственные числа (решетки Лавеса)
[ редактировать ]
Решетки Лавеса являются двойниками архимедовых решеток. Рисунки из. [ 6 ] См. также Равномерные мозаики .
| Решетка | С | Порог проникновения сайта | Порог перколяции облигаций | |
|---|---|---|---|---|
| Каир пятиугольный
Д(3 2 ,4,3,4)=( 2 ⁄ 3 )(5 3 )+( 1 ⁄ 3 )(5 4 ) |
3,4 | 3 1 ⁄ 3 | 0.6501834(2), [ 11 ] 0.650184(5) [ 6 ] | 0,585863... = 1 - п с связь (3 2 ,4,3,4) |
| Пятиугольный D(3 3 ,4 2 )=( 1 ⁄ 3 )(5 4 )+( 2 ⁄ 3 )(5 3 ) | 3,4 | 3 1 ⁄ 3 | 0.6470471(2), [ 11 ] 0.647084(5), [ 6 ] 0.6471(6) [ 38 ] | 0,580358... = 1 - п с связь (3 3 ,4 2 ), 0.5800(6) [ 38 ] |
| Д(3 4 ,6)=( 1 ⁄ 5 )(4 6 )+( 4 ⁄ 5 )(4 3 ) | 3,6 | 3 3 ⁄ 5 | 0.639447 [ 6 ] | 0,565694... = 1 - п с связь (3 4 ,6 ) |
| игральные кости, ромбовидная мозаика
Д(3,6,3,6) = ( 1 ⁄ 3 )(4 6 ) + ( 2 ⁄ 3 )(4 3 ) |
3,6 | 4 | 0.5851(4), [ 66 ] 0.585040(5) [ 6 ] | 0,475595... = 1 - п с связь (3,6,3,6 ) |
| рубиновый двойной
Д(3,4,6,4) = ( 1 ⁄ 6 )(4 6 ) + ( 2 ⁄ 6 )(4 3 ) + ( 3 ⁄ 6 )(4 4 ) |
3,4,6 | 4 | 0.582410(5) [ 6 ] | 0,475167... = 1 - п с связь (3,4,6,4 ) |
| Юнион Джек, квадратная плитка Тетракис
Д(4,8 2 ) = ( 1 ⁄ 2 )(3 4 ) + ( 1 ⁄ 2 )(3 8 ) |
4,8 | 6 | 1 ⁄ 2 | 0,323197... = 1 - п с связь (4,8 2 ) |
| разделенный пополам шестиугольник, [ 67 ] крест двойной
Д(4,6,12)= ( 1 ⁄ 6 )(3 12 )+( 2 ⁄ 6 )(3 6 )+( 1 ⁄ 2 )(3 4 ) |
4,6,12 | 6 | 1 ⁄ 2 | 0,306266... = 1 - п с связь (4,6,12) |
| асаноха (лист конопли) [ 68 ]
Д(3, 12 2 )=( 2 ⁄ 3 )(3 3 )+( 1 ⁄ 3 )(3 12 ) |
3,12 | 6 | 1 ⁄ 2 | 0,259579... = 1 - п с связь (3, 12 2 ) |
2-однородные решетки
[ редактировать ]Топ-3 решетки: №13 №12 №36
Нижние 3 решетки: №34 №37 №11
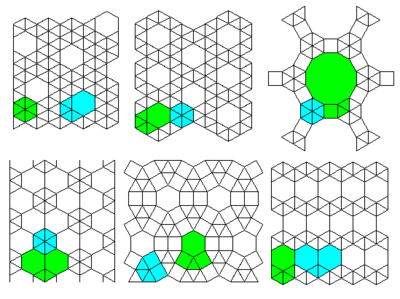
Две верхние решетки: №35 №30
Нижние 2 решетки: #41 #42

Топ-4 решетки: №22 №23 №21 №20
Нижние 3 решетки: №16 №17 №15

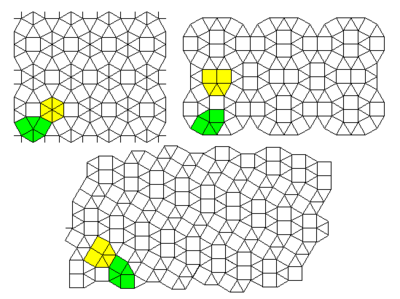
Две верхние решетки: №31 №32
Нижняя решетка: #33
| # | Решетка | С | Порог проникновения сайта | Порог перколяции облигаций | |
|---|---|---|---|---|---|
| 41 | ( 1 ⁄ 2 )(3,4,3,12) + ( 1 ⁄ 2 )(3, 12 2 ) | 4,3 | 3.5 | 0.7680(2) [ 69 ] | 0.67493252(36) [ нужна ссылка ] |
| 42 | ( 1 ⁄ 3 )(3,4,6,4) + ( 2 ⁄ 3 )(4,6,12) | 4,3 | 3 1 ⁄ 3 | 0.7157(2) [ 69 ] | 0.64536587(40) [ нужна ссылка ] |
| 36 | ( 1 ⁄ 7 )(3 6 ) + ( 6 ⁄ 7 )(3 2 ,4,12) | 6,4 | 4 2 ⁄ 7 | 0.6808(2) [ 69 ] | 0.55778329(40) [ нужна ссылка ] |
| 15 | ( 2 ⁄ 3 )(3 2 ,6 2 ) + ( 1 ⁄ 3 )(3,6,3,6) | 4,4 | 4 | 0.6499(2) [ 69 ] | 0.53632487(40) [ нужна ссылка ] |
| 34 | ( 1 ⁄ 7 )(3 6 ) + ( 6 ⁄ 7 )(3 2 ,6 2 ) | 6,4 | 4 2 ⁄ 7 | 0.6329(2) [ 69 ] | 0.51707873(70) [ нужна ссылка ] |
| 16 | ( 4 ⁄ 5 )(3,4 2 ,6) + ( 1 ⁄ 5 )(3,6,3,6) | 4,4 | 4 | 0.6286(2) [ 69 ] | 0.51891529(35) [ нужна ссылка ] |
| 17 | ( 4 ⁄ 5 )(3,4 2 ,6) + ( 1 ⁄ 5 )(3,6,3,6)* | 4,4 | 4 | 0.6279(2) [ 69 ] | 0.51769462(35) [ нужна ссылка ] |
| 35 | ( 2 ⁄ 3 )(3,4 2 ,6) + ( 1 ⁄ 3 )(3,4,6,4) | 4,4 | 4 | 0.6221(2) [ 69 ] | 0.51973831(40) [ нужна ссылка ] |
| 11 | ( 1 ⁄ 2 )(3 4 ,6) + ( 1 ⁄ 2 )(3 2 ,6 2 ) | 5,4 | 4.5 | 0.6171(2) [ 69 ] | 0.48921280(37) [ нужна ссылка ] |
| 37 | ( 1 ⁄ 2 )(3 3 ,4 2 ) + ( 1 ⁄ 2 )(3,4,6,4) | 5,4 | 4.5 | 0.5885(2) [ 69 ] | 0.47229486(38) [ нужна ссылка ] |
| 30 | ( 1 ⁄ 2 )(3 2 ,4,3,4) + ( 1 ⁄ 2 )(3,4,6,4) | 5,4 | 4.5 | 0.5883(2) [ 69 ] | 0.46573078(72) [ нужна ссылка ] |
| 23 | ( 1 ⁄ 2 )(3 3 ,4 2 ) + ( 1 ⁄ 2 )(4 4 ) | 5,4 | 4.5 | 0.5720(2) [ 69 ] | 0.45844622(40) [ нужна ссылка ] |
| 22 | ( 2 ⁄ 3 )(3 3 ,4 2 ) + ( 1 ⁄ 3 )(4 4 ) | 5,4 | 4 2 ⁄ 3 | 0.5648(2) [ 69 ] | 0.44528611(40) [ нужна ссылка ] |
| 12 | ( 1 ⁄ 4 )(3 6 ) + ( 3 ⁄ 4 )(3 4 ,6) | 6,5 | 5 1 ⁄ 4 | 0.5607(2) [ 69 ] | 0.41109890(37) [ нужна ссылка ] |
| 33 | ( 1 ⁄ 2 )(3 3 ,4 2 ) + ( 1 ⁄ 2 )(3 2 ,4,3,4) | 5,5 | 5 | 0.5505(2) [ 69 ] | 0.41628021(35) [ нужна ссылка ] |
| 32 | ( 1 ⁄ 3 )(3 3 ,4 2 ) + ( 2 ⁄ 3 )(3 2 ,4,3,4) | 5,5 | 5 | 0.5504(2) [ 69 ] | 0.41549285(36) [ нужна ссылка ] |
| 31 | ( 1 ⁄ 7 )(3 6 ) + ( 6 ⁄ 7 )(3 2 ,4,3,4) | 6,5 | 5 1 ⁄ 7 | 0.5440(2) [ 69 ] | 0.40379585(40) [ нужна ссылка ] |
| 13 | ( 1 ⁄ 2 )(3 6 ) + ( 1 ⁄ 2 )(3 4 ,6) | 6,5 | 5.5 | 0.5407(2) [ 69 ] | 0.38914898(35) [ нужна ссылка ] |
| 21 | ( 1 ⁄ 3 )(3 6 ) + ( 2 ⁄ 3 )(3 3 ,4 2 ) | 6,5 | 5 1 ⁄ 3 | 0.5342(2) [ 69 ] | 0.39491996(40) [ нужна ссылка ] |
| 20 | ( 1 ⁄ 2 )(3 6 ) + ( 1 ⁄ 2 )(3 3 ,4 2 ) | 6,5 | 5.5 | 0.5258(2) [ 69 ] | 0.38285085(38) [ нужна ссылка ] |
Неоднородная 2-однородная решетка
[ редактировать ]
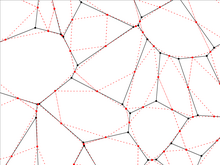
На этом рисунке показано нечто похожее на 2-однородную решетку № 37, за исключением того, что не все многоугольники правильные — на месте двух квадратов находится прямоугольник — и размер многоугольников изменен. Эта решетка находится в изорадиальном представлении, в котором каждый многоугольник вписан в окружность единичного радиуса. Два квадрата в 2-однородной решетке теперь должны быть представлены как один прямоугольник, чтобы удовлетворить условию изорадиальности. Решетка показана черными краями, а двойственная решетка - красными пунктирными линиями. Зеленые кружки показывают изорадиальные ограничения как на исходную, так и на двойственную решетки. Желтые многоугольники выделяют три типа многоугольников на решетке, а розовые многоугольники выделяют два типа многоугольников на двойной решетке. Решетка имеет типы вершин ( 1 ⁄ 2 )(3 3 ,4 2 ) + ( 1 ⁄ 2 )(3,4,6,4), а двойственная решетка имеет типы вершин ( 1 ⁄ 15 )(4 6 )+( 6 ⁄ 15 )(4 2 ,5 2 )+( 2 ⁄ 15 )(5 3 )+( 6 ⁄ 15 )(5 2 ,4). Критическая точка заключается в том, что более длинные связи (как в решетке, так и в двойной решетке) имеют вероятность заполнения p = 2 sin (π/18) = 0,347296... что является порогом перколяции связи в треугольной решетке, а более короткие связи имеют вероятность заполнения 1 - 2 sin(π/18) = 0,652703..., что представляет собой перколяцию связей в гексагональной решетке. Эти результаты следуют из изорадиального условия [ 70 ] но также следуют из применения преобразования звезда-треугольник к некоторым звездам на сотовой решетке. Наконец, его можно обобщить до трех разных вероятностей в трех разных направлениях: p 1 , p 2 и p 3 для длинных связей и 1 − p 1 , 1 − p 2 и 1 − p 3 для коротких связей. , где p 1 , p 2 и p 3 удовлетворяют критической поверхности неоднородной треугольной решетки.
Пороги на 2D решетках для галстука-бабочки и мартини
[ редактировать ]Слева, в центре и справа расположены: решетка для мартини, решетка для мартини-А, решетка для мартини-Б. Внизу: покрытие мартини/медиальная решетка, такая же, как подсеть 2×2, 1×1 для решеток типа кагоме (удалена).

Некоторые другие примеры обобщенных решеток-бабочек (ad) и двойственных решеток (eh):

| Решетка | С | Порог проникновения сайта | Порог перколяции облигаций | |
|---|---|---|---|---|
| мартини ( 3 ⁄ 4 )(3,9 2 )+( 1 ⁄ 4 )(9 3 ) | 3 | 3 | 0,764826..., 1 + р 4 − 3 п. 3 = 0 [ 71 ] | 0.707107... = 1/ √ 2 [ 72 ] |
| галстук-бабочка (с) | 3,4 | 3 1 ⁄ 7 | 0,672929..., 1 - 2 п. 3 − 14:00 4 − 14:00 5 − 7 п. 6 + 18 р 7 + 11 п. 8 − 35 р. 9 + 21 п. 10 − 4 п. 11 = 0 [ 73 ] | |
| галстук-бабочка (д) | 3,4 | 3 1 ⁄ 3 | 0,625457..., 1 - 2 п. 2 − 3 п. 3 + 4 п. 4 − п 5 = 0 [ 73 ] | |
| мартини-А ( 2 ⁄ 3 )(3,7 2 )+( 1 ⁄ 3 )(3,7 3 ) | 3,4 | 3 1 ⁄ 3 | 1/ √ 2 [ 73 ] | 0,625457..., 1 - 2 п. 2 − 3 п. 3 + 4 п. 4 − п 5 = 0 [ 73 ] |
| двойной галстук-бабочка (e) | 3,4 | 3 2 ⁄ 3 | 0,595482..., 1-р в связь (галстук-бабочка(а)) [ 73 ] | |
| галстук-бабочка (б) | 3,4,6 | 3 2 ⁄ 3 | 0,533213..., 1 - р - 2 р 3 -4р 4 -4р 5 +15 6 + 13р 7 -36р 8 +19р 9 + р 10 + р 11 =0 [ 73 ] | |
| покрытие для мартини/медиальная ( 1 ⁄ 2 )(3 3 ,9) + ( 1 ⁄ 2 )(3,9,3,9) | 4 | 4 | 0.707107... = 1/ √ 2 [ 72 ] | 0.57086651(33) [ нужна ссылка ] |
| мартини-Б ( 1 ⁄ 2 )(3,5,3,5 2 ) + ( 1 ⁄ 2 )(3,5 2 ) | 3, 5 | 4 | 0,618034... = 2/(1 + √ 5 ), 1- р 2 - р = 0 [ 71 ] [ 73 ] | 1 ⁄ 2 [ 72 ] [ 73 ] |
| галстук-бабочка двойной (f) | 3,4,8 | 4 2 ⁄ 5 | 0,466787..., 1 - п с связь (галстук-бабочка (б)) [ 73 ] | |
| галстук-бабочка (а)( 1 ⁄ 2 )(3 2 ,4,3 2 ,4) + ( 1 ⁄ 2 )(3,4,3) | 4,6 | 5 | 0.5472(2), [ 38 ] 0.5479148(7) [ 74 ] | 0,404518..., 1 - р - 6 р 2 + 18:00 3 − п 5 = 0 [ 73 ] [ 75 ] |
| галстук-бабочка двойной (h) | 3,6,8 | 5 | 0,374543..., 1 - п с связь (галстук-бабочка (д)) [ 73 ] | |
| галстук-бабочка двойной (г) | 3,6,10 | 5 1 ⁄ 2 | 0,547... = р с сайт (галстук-бабочка(а)) | 0,327071..., 1 - п с связь (галстук-бабочка (с)) [ 73 ] |
| мартини дуал ( 1 ⁄ 2 )(3 3 ) + ( 1 ⁄ 2 )(3 9 ) | 3,9 | 6 | 1 ⁄ 2 | 0.292893... = 1 − 1/ √ 2 [ 72 ] |
Пороги на двумерных покрывающих, медиальных и совпадающих решетках
[ редактировать ]| Решетка | С | Порог проникновения сайта | Порог перколяции облигаций | |
|---|---|---|---|---|
| (4, 6, 12) покрывающие/медиальные | 4 | 4 | п с связь (4, 6, 12) = 0.693731... | 0.5593140(2), [ 11 ] 0.559315(1) [ нужна ссылка ] |
| (4, 8 2 ) покрывающее/медиальное, квадратное кагоме | 4 | 4 | п с связь (4,8 2 ) = 0.676803... | 0.544798017(4), [ 11 ] 0.54479793(34) [ нужна ссылка ] |
| (3 4 , 6) медиальный | 4 | 4 | 0.5247495(5) [ 11 ] | |
| (3,4,6,4) медиальный | 4 | 4 | 0.51276 [ 11 ] | |
| (3 2 , 4, 3, 4) медиальный | 4 | 4 | 0.512682929(8) [ 11 ] | |
| (3 3 , 4 2 ) медиальный | 4 | 4 | 0.5125245984(9) [ 11 ] | |
| квадратное покрытие (неплоское) | 6 | 6 | 1 ⁄ 2 | 0.3371(1) [ 56 ] |
| квадратная решетка соответствия (неплоская) | 8 | 8 | 1 - п с сайт (квадрат) = 0,407253... | 0.25036834(6) [ 18 ] |
Пороги на двумерных химерных неплоских решетках
[ редактировать ]| Решетка | С | Порог проникновения сайта | Порог перколяции облигаций | |
|---|---|---|---|---|
| К(2,2) | 4 | 4 | 0.51253(14) [ 78 ] | 0.44778(15) [ 78 ] |
| К(3,3) | 6 | 6 | 0.43760(15) [ 78 ] | 0.35502(15) [ 78 ] |
| К(4,4) | 8 | 8 | 0.38675(7) [ 78 ] | 0.29427(12) [ 78 ] |
| К(5,5) | 10 | 10 | 0.35115(13) [ 78 ] | 0.25159(13) [ 78 ] |
| К(6,6) | 12 | 12 | 0.32232(13) [ 78 ] | 0.21942(11) [ 78 ] |
| К(7,7) | 14 | 14 | 0.30052(14) [ 78 ] | 0.19475(9) [ 78 ] |
| К(8,8) | 16 | 16 | 0.28103(11) [ 78 ] | 0.17496(10) [ 78 ] |
Пороги на решетках подсетей
[ редактировать ]
Решетки кагоме подсетей 2 x 2, 3 x 3 и 4 x 4. Подсеть 2 × 2 также известна как решетка «треугольного кагоме». [ 79 ]
| Решетка | С | Порог проникновения сайта | Порог перколяции облигаций | |
|---|---|---|---|---|
| шахматная доска — подсеть 2 × 2 | 4,3 | 0.596303(1) [ 80 ] | ||
| шахматная доска — подсеть 4 × 4 | 4,3 | 0.633685(9) [ 80 ] | ||
| шахматная доска — подсеть 8 × 8 | 4,3 | 0.642318(5) [ 80 ] | ||
| шахматная доска — подсеть 16 × 16 | 4,3 | 0.64237(1) [ 80 ] | ||
| шахматная доска — подсеть 32 × 32 | 4,3 | 0.64219(2) [ 80 ] | ||
| шахматная доска – подсеть | 4,3 | 0.642216(10) [ 80 ] | ||
| кагоме – подсеть 2 × 2 = (3, 12 2 ) покрывающий/медиальный | 4 | п с связь (3, 12 2 ) = 0.74042077... | 0.600861966960(2), [ 11 ] 0.6008624(10), [ 19 ] 0.60086193(3) [ 9 ] | |
| кагоме – подсеть 3×3 | 4 | 0.6193296(10), [ 19 ] 0.61933176(5), [ 9 ] 0.61933044(32) [ нужна ссылка ] | ||
| кагоме – подсеть 4 × 4 | 4 | 0.625365(3), [ 19 ] 0.62536424(7) [ 9 ] | ||
| кагоме – подсеть | 4 | 0.628961(2) [ 19 ] | ||
| кагоме – (1 × 1): (2 × 2) подсеть = покрытие мартини/медиальная часть | 4 | п с связь (мартини) = 1/ √ 2 = 0,707107... | 0.57086648(36) [ нужна ссылка ] | |
| кагоме – (1 × 1): (3 × 3) подсеть | 4,3 | 0.728355596425196... [ 9 ] | 0.58609776(37) [ нужна ссылка ] | |
| кагоме – (1 × 1): (4 × 4) подсеть | 0.738348473943256... [ 9 ] | |||
| кагоме – (1 × 1): (5 × 5) подсеть | 0.743548682503071... [ 9 ] | |||
| кагоме – (1 × 1): (6 × 6) подсеть | 0.746418147634282... [ 9 ] | |||
| кагоме – (2 × 2): (3 × 3) подсеть | 0.61091770(30) [ нужна ссылка ] | |||
| треугольный – подсеть 2 × 2 | 6,4 | 0.471628788 [ 80 ] | ||
| треугольный – подсеть 3 × 3 | 6,4 | 0.509077793 [ 80 ] | ||
| треугольный – подсеть 4 × 4 | 6,4 | 0.524364822 [ 80 ] | ||
| треугольный – подсеть 5 × 5 | 6,4 | 0.5315976(10) [ 80 ] | ||
| треугольный – подсеть | 6,4 | 0.53993(1) [ 80 ] |
Пороги случайных последовательно адсорбируемых объектов
[ редактировать ](Дополнительные результаты и сравнение с плотностью застревания см. в разделе « Случайная последовательная адсорбция »).
| система | С | Порог сайта |
|---|---|---|
| димеры на сотовой решетке | 3 | 0.69, [ 81 ] 0.6653 [ 82 ] |
| димеры на треугольной решетке | 6 | 0.4872(8), [ 81 ] 0.4873, [ 82 ] |
| выровненные линейные димеры на треугольной решетке | 6 | 0.5157(2) [ 83 ] |
| выровненные линейные 4-меры на треугольной решетке | 6 | 0.5220(2) [ 83 ] |
| выровненные линейные 8-меры на треугольной решетке | 6 | 0.5281(5) [ 83 ] |
| выровненные линейные 12-меры на треугольной решетке | 6 | 0.5298(8) [ 83 ] |
| линейные 16-меры на треугольной решетке | 6 | выровнено 0,5328(7) [ 83 ] |
| линейные 32-меры на треугольной решетке | 6 | выровнено 0,5407(6) [ 83 ] |
| линейные 64-меры на треугольной решетке | 6 | выровнено 0,5455(4) [ 83 ] |
| выровненные линейные 80-меры на треугольной решетке | 6 | 0.5500(6) [ 83 ] |
| выровненный линейный k на треугольной решетке | 6 | 0.582(9) [ 83 ] |
| димеры и 5% примесей, треугольная решетка | 6 | 0.4832(7) [ 84 ] |
| параллельные димеры на квадратной решетке | 4 | 0.5863 [ 85 ] |
| димеры на квадратной решетке | 4 | 0.5617, [ 85 ] 0.5618(1), [ 86 ] 0.562, [ 87 ] 0.5713 [ 82 ] |
| линейные 3-меры на квадратной решетке | 4 | 0.528 [ 87 ] |
| 3-х узл., угол 120°, 5% примесей, треугольная решетка. | 6 | 0.4574(9) [ 84 ] |
| 3-узловые треугольники, 5% примесей, треугольная решетка. | 6 | 0.5222(9) [ 84 ] |
| линейные тримеры и 5% примесей, треугольная решетка | 6 | 0.4603(8) [ 84 ] |
| линейные 4-меры на квадратной решетке | 4 | 0.504 [ 87 ] |
| линейные 5-меры на квадратной решетке | 4 | 0.490 [ 87 ] |
| линейные 6-меры на квадратной решетке | 4 | 0.479 [ 87 ] |
| линейные 8-меры на квадратной решетке | 4 | 0.474, [ 87 ] 0.4697(1) [ 86 ] |
| линейные 10-меры на квадратной решетке | 4 | 0.469 [ 87 ] |
| линейные 16-меры на квадратной решетке | 4 | 0.4639(1) [ 86 ] |
| линейные 32-меры на квадратной решетке | 4 | 0.4747(2) [ 86 ] |
Порог определяет долю сайтов, занимаемых объектами, когда происходит первое проникновение сайтов (не при полном заклинивании). Более длинные k-меры см. в работе. [ 88 ]
Пороги полных димерных накрытий двумерных решеток
[ редактировать ]Здесь мы имеем дело с сетками, которые получаются путем покрытия решетки димерами, а затем рассматриваем перколяцию связей по остальным связям. В дискретной математике эта проблема известна как проблема «идеального соответствия» или «проблемы димерного покрытия».
| система | С | Порог облигации |
|---|---|---|
| Параллельное покрытие, квадратная решетка | 6 | 0.381966... [ 89 ] |
| Сдвижное покрытие, квадратная решетка | 6 | 0.347296... [ 89 ] |
| Ступенчатое покрытие, квадратная решетка | 6 | 0.376825(2) [ 89 ] |
| Случайное покрытие, квадратная решетка | 6 | 0.367713(2) [ 89 ] |
| Параллельное покрытие, треугольная решетка | 10 | 0.237418... [ 89 ] |
| Ступенчатое покрытие, треугольная решетка | 10 | 0.237497(2) [ 89 ] |
| Случайное покрытие, треугольная решетка | 10 | 0.235340(1) [ 89 ] |
Пороги полимеров (случайные блуждания) на квадратной решетке
[ редактировать ]Система состоит из обычных (неизбегающих) случайных блужданий длины l по квадратной решетке. [ 90 ]
| l (длина полимера) | С | Проникновение облигаций |
|---|---|---|
| 1 | 4 | 0,5 (точно) [ 91 ] |
| 2 | 4 | 0.47697(4) [ 91 ] |
| 4 | 4 | 0.44892(6) [ 91 ] |
| 8 | 4 | 0.41880(4) [ 91 ] |
Пороги самоизбегающих блужданий длины k, добавленные случайной последовательной адсорбцией
[ редактировать ]| к | С | Пороги сайта | Пороги облигаций |
|---|---|---|---|
| 1 | 4 | 0.593(2) [ 92 ] | 0.5009(2) [ 92 ] |
| 2 | 4 | 0.564(2) [ 92 ] | 0.4859(2) [ 92 ] |
| 3 | 4 | 0.552(2) [ 92 ] | 0.4732(2) [ 92 ] |
| 4 | 4 | 0.542(2) [ 92 ] | 0.4630(2) [ 92 ] |
| 5 | 4 | 0.531(2) [ 92 ] | 0.4565(2) [ 92 ] |
| 6 | 4 | 0.522(2) [ 92 ] | 0.4497(2) [ 92 ] |
| 7 | 4 | 0.511(2) [ 92 ] | 0.4423(2) [ 92 ] |
| 8 | 4 | 0.502(2) [ 92 ] | 0.4348(2) [ 92 ] |
| 9 | 4 | 0.493(2) [ 92 ] | 0.4291(2) [ 92 ] |
| 10 | 4 | 0.488(2) [ 92 ] | 0.4232(2) [ 92 ] |
| 11 | 4 | 0.482(2) [ 92 ] | 0.4159(2) [ 92 ] |
| 12 | 4 | 0.476(2) [ 92 ] | 0.4114(2) [ 92 ] |
| 13 | 4 | 0.471(2) [ 92 ] | 0.4061(2) [ 92 ] |
| 14 | 4 | 0.467(2) [ 92 ] | 0.4011(2) [ 92 ] |
| 15 | 4 | 0.4011(2) [ 92 ] | 0.3979(2) [ 92 ] |
Пороги на двумерных неоднородных решетках
[ редактировать ]| Решетка | С | Порог проникновения сайта | Порог перколяции облигаций |
|---|---|---|---|
| галстук-бабочка с p = 1 ⁄ 2 на одной недиагональной связи | 3 | 0.3819654(5), [ 93 ] [ 56 ] |
Пороги для 2D-моделей континуума
[ редактировать ]| Система | Φ с | η с | н с |
|---|---|---|---|
| Диски радиуса r | 0.67634831(2), [ 94 ] 0.6763475(6), [ 95 ] 0.676339(4), [ 96 ] 0.6764(4), [ 97 ] 0.6766(5), [ 98 ] 0.676(2), [ 99 ] 0.679, [ 100 ] 0.674 [ 101 ] 0.676, [ 102 ] 0.680 [ 103 ] | 1.1280867(5), [ 104 ] 1.1276(9), [ 105 ] 1.12808737(6), [ 94 ] 1.128085(2), [ 95 ] 1.128059(12), [ 96 ] 1.13, [ нужна ссылка ] 0.8 [ 106 ] | 1.43632505(10), [ 107 ] 1.43632545(8), [ 94 ] 1.436322(2), [ 95 ] 1.436289(16), [ 96 ] 1.436320(4), [ 108 ] 1.436323(3), [ 109 ] 1.438(2), [ 110 ] 1.216 (48) [ 111 ] |
| Эллипсы, ε = 1,5 | 0.0043 [ 100 ] | 0.00431 | 2.059081(7) [ 109 ] |
| Эллипсы, ε = 5 ⁄ 3 | 0.65 [ 112 ] | 1.05 [ 112 ] | 2.28 [ 112 ] |
| Эллипсы, ε = 2 | 0.6287945(12), [ 109 ] 0.63 [ 112 ] | 0.991000(3), [ 109 ] 0.99 [ 112 ] | 2.523560(8), [ 109 ] 2.5 [ 112 ] |
| Эллипсы, ε = 3 | 0.56 [ 112 ] | 0.82 [ 112 ] | 3.157339(8), [ 109 ] 3.14 [ 112 ] |
| Эллипсы, ε = 4 | 0.5 [ 112 ] | 0.69 [ 112 ] | 3.569706(8), [ 109 ] 3.5 [ 112 ] |
| Эллипсы, ε = 5 | 0.455, [ 100 ] 0.455, [ 102 ] 0.46 [ 112 ] | 0.607 [ 100 ] | 3.861262(12), [ 109 ] 3.86 [ 100 ] |
| Эллипсы, ε = 6 | 4.079365(17) [ 109 ] | ||
| Эллипсы, ε = 7 | 4.249132(16) [ 109 ] | ||
| Эллипсы, ε = 8 | 4.385302(15) [ 109 ] | ||
| Эллипсы, ε = 9 | 4.497000(8) [ 109 ] | ||
| Эллипсы, ε = 10 | 0.301, [ 100 ] 0.303, [ 102 ] 0.30 [ 112 ] | 0.358 [ 100 ] 0.36 [ 112 ] | 4.590416(23) [ 109 ] 4.56, [ 100 ] 4.5 [ 112 ] |
| Эллипсы, ε = 15 | 4.894752(30) [ 109 ] | ||
| Эллипсы, ε = 20 | 0.178, [ 100 ] 0.17 [ 112 ] | 0.196 [ 100 ] | 5.062313(39), [ 109 ] 4.99 [ 100 ] |
| Эллипсы, ε = 50 | 0.081 [ 100 ] | 0.084 [ 100 ] | 5.393863(28), [ 109 ] 5.38 [ 100 ] |
| Эллипсы, ε = 100 | 0.0417 [ 100 ] | 0.0426 [ 100 ] | 5.513464(40), [ 109 ] 5.42 [ 100 ] |
| Эллипсы, ε = 200 | 0.021 [ 112 ] | 0.0212 [ 112 ] | 5.40 [ 112 ] |
| Эллипсы, ε = 1000 | 0.0043 [ 100 ] | 0.00431 | 5.624756(22), [ 109 ] 5.5 |
| Суперэллипсы, ε = 1, m = 1,5 | 0.671 [ 102 ] | ||
| Суперэллипсы, ε = 2,5, m = 1,5 | 0.599 [ 102 ] | ||
| Суперэллипсы, ε = 5, m = 1,5 | 0.469 [ 102 ] | ||
| Суперэллипсы, ε = 10, m = 1,5 | 0.322 [ 102 ] | ||
| диск-прямоугольник, ε = 1,5 | 1.894 [ 108 ] | ||
| диск-прямоугольник, ε = 2 | 2.245 [ 108 ] | ||
| Выровненные квадраты стороны | 0.66675(2), [ 52 ] 0.66674349(3), [ 94 ] 0.66653(1), [ 113 ] 0.6666(4), [ 114 ] 0.668 [ 101 ] | 1.09884280(9), [ 94 ] 1.0982(3), [ 113 ] 1.098(1) [ 114 ] | 1.09884280(9), [ 94 ] 1.0982(3), [ 113 ] 1.098(1) [ 114 ] |
| Случайно ориентированные квадраты | 0.62554075(4), [ 94 ] 0.6254(2) [ 114 ] 0.625, [ 102 ] | 0.9822723(1), [ 94 ] 0.9819(6) [ 114 ] 0.982278(14) [ 115 ] | 0.9822723(1), [ 94 ] 0.9819(6) [ 114 ] 0.982278(14) [ 115 ] |
| Случайно ориентированные квадраты внутри угла | 0.6255(1) [ 114 ] | 0.98216(15) [ 114 ] | |
| Прямоугольники, ε = 1,1 | 0.624870(7) | 0.980484(19) | 1.078532(21) [ 115 ] |
| Прямоугольники, ε = 2 | 0.590635(5) | 0.893147(13) | 1.786294(26) [ 115 ] |
| Прямоугольники, ε = 3 | 0.5405983(34) | 0.777830(7) | 2.333491(22) [ 115 ] |
| Прямоугольники, ε = 4 | 0.4948145(38) | 0.682830(8) | 2.731318(30) [ 115 ] |
| Прямоугольники, ε = 5 | 0.4551398(31), 0.451 [ 102 ] | 0.607226(6) | 3.036130(28) [ 115 ] |
| Прямоугольники, ε = 10 | 0.3233507(25), 0.319 [ 102 ] | 0.3906022(37) | 3.906022(37) [ 115 ] |
| Прямоугольники, ε = 20 | 0.2048518(22) | 0.2292268(27) | 4.584535(54) [ 115 ] |
| Прямоугольники, ε = 50 | 0.09785513(36) | 0.1029802(4) | 5.149008(20) [ 115 ] |
| Прямоугольники, ε = 100 | 0.0523676(6) | 0.0537886(6) | 5.378856(60) [ 115 ] |
| Прямоугольники, ε = 200 | 0.02714526(34) | 0.02752050(35) | 5.504099(69) [ 115 ] |
| Прямоугольники, ε = 1000 | 0.00559424(6) | 0.00560995(6) | 5.609947(60) [ 115 ] |
| Палочки (иголки) длины | 5.63726(2), [ 116 ] 5.6372858(6), [ 94 ] 5.637263(11), [ 115 ] 5.63724(18) [ 117 ] | ||
| палочки логнормальной длины расст. Стандарт = 0,5 | 4.756(3) [ 117 ] | ||
| палочки с коррелированным углом расст. с=0,5 | 6.6076(4) [ 117 ] | ||
| Степенные диски, x = 2,05 | 0.993(1) [ 118 ] | 4.90(1) | 0.0380(6) |
| Степенные диски, x = 2,25 | 0.8591(5) [ 118 ] | 1.959(5) | 0.06930(12) |
| Степенные диски, x = 2,5 | 0.7836(4) [ 118 ] | 1.5307(17) | 0.09745(11) |
| Степенные диски, x = 4 | 0.69543(6) [ 118 ] | 1.18853(19) | 0.18916(3) |
| Степенные диски, x = 5 | 0.68643(13) [ 118 ] | 1.1597(3) | 0.22149(8) |
| Степенные диски, x = 6 | 0.68241(8) [ 118 ] | 1.1470(1) | 0.24340(5) |
| Степенные диски, x = 7 | 0.6803(8) [ 118 ] | 1.140(6) | 0.25933(16) |
| Степенные диски, x = 8 | 0.67917(9) [ 118 ] | 1.1368(5) | 0.27140(7) |
| Степенные диски, x = 9 | 0.67856(12) [ 118 ] | 1.1349(4) | 0.28098(9) |
| Пустоты вокруг дисков радиуса r | 1 − Φ c (диск) = 0,32355169(2), [ 94 ] 0.318(2), [ 119 ] 0.3261(6) [ 120 ] |


Для дисков, равно критическому числу дисков на единицу площади, измеряемому в единицах диаметра. , где количество объектов и размер системы
Для дисков, равна критической общей площади диска.
дает число центров диска внутри круга влияния (радиус 2 r).
– критический радиус диска.
для эллипсов большой и малой полуосей a и b соответственно. Соотношение сторон с .
для прямоугольников размеров и . Соотношение сторон с .
для степенных распределенных дисков с , .
равна доле критической площади.
Для дисков см. [ 99 ] использовать где - плотность дисков радиуса .
равно количеству объектов максимальной длины за единицу площади.
Для эллипсов
Для просачивания пустот, – критическая доля пустот.
Дополнительные значения эллипса см. [ 109 ] [ 112 ]
Дополнительные значения прямоугольников см. [ 115 ]
И эллипсы, и прямоугольники относятся к суперэллипсам, причем . Дополнительные значения перколяции суперэллипсов см. [ 102 ]
Для монодисперсных систем частиц пороги перколяции супердисков вогнутой формы получены, как показано на рис. [ 121 ]
О двоичных дисперсиях дисков см. [ 95 ] [ 122 ] [ 123 ]
Пороги для двумерных случайных и квазирешеток
[ редактировать ]




| Решетка | С | Порог проникновения сайта | Порог перколяции облигаций | |
|---|---|---|---|---|
| Граф относительной окрестности | 2.5576 | 0.796(2) [ 124 ] | 0.771(2) [ 124 ] | |
| Мозаика Вороного | 3 | 0.71410(2), [ 126 ] 0.7151* [ 69 ] | 0.68, [ 127 ] 0.6670(1), [ 128 ] 0.6680(5), [ 129 ] 0.666931(5) [ 126 ] | |
| Покрытие Вороного/медиальное | 4 | 0.666931(2) [ 126 ] [ 128 ] | 0.53618(2) [ 126 ] | |
| Рандомизированное кагоме/квадрат-восьмиугольник, фракция r= 1 ⁄ 2 | 4 | 0.6599 [ 16 ] | ||
| Ромб Пенроуза двойной | 4 | 0.6381(3) [ 66 ] | 0.5233(2) [ 66 ] | |
| График Габриэля | 4 | 0.6348(8), [ 130 ] 0.62 [ 131 ] | 0.5167(6), [ 130 ] 0.52 [ 131 ] | |
| Мозаика случайными линиями, двойная | 4 | 0.586(2) [ 132 ] | ||
| Ромб Пенроуза | 4 | 0.5837(3), [ 66 ] 0.0.5610(6) (взвешенные облигации) [ 133 ] 0.58391(1) [ 134 ] | 0.483(5), [ 135 ] 0.4770(2) [ 66 ] | |
| Восьмиугольная решетка, «химические» связи ( плитка Аммана – Бинкера ) | 4 | 0.585 [ 136 ] | 0.48 [ 136 ] | |
| Восьмиугольная решетка, «ферромагнитные» звенья. | 5.17 | 0.543 [ 136 ] | 0.40 [ 136 ] | |
| Додекагональная решетка, «химические» звенья | 3.63 | 0.628 [ 136 ] | 0.54 [ 136 ] | |
| Додекагональная решетка, «ферромагнитные» звенья. | 4.27 | 0.617 [ 136 ] | 0.495 [ 136 ] | |
| Триангуляция Делоне | 6 | 1 ⁄ 2 [ 137 ] | 0.3333(1) [ 128 ] 0.3326(5), [ 129 ] 0.333069(2) [ 126 ] | |
| Равномерная бесконечная плоская триангуляция [ 138 ] | 6 | 1 ⁄ 2 | (2 √ 3 – 1)/11 ≈ 0.2240 [ 125 ] [ 139 ] |
*Теоретическая оценка
Пороги в 2D-коррелированных системах
[ редактировать ]Предполагая степенные корреляции
| решетка | а | Порог проникновения сайта | Порог перколяции облигаций |
|---|---|---|---|
| квадрат | 3 | 0.561406(4) [ 140 ] | |
| квадрат | 2 | 0.550143(5) [ 140 ] | |
| квадрат | 0.1 | 0.508(4) [ 140 ] |
Пороги на плитах
[ редактировать ]h — толщина плиты, h × ∞ × ∞. Граничные условия (bc) относятся к верхней и нижней плоскостям плиты.
| Решетка | час | С | Порог проникновения сайта | Порог перколяции облигаций | |
|---|---|---|---|---|---|
| простой кубический (открытый до н.э.) | 2 | 5 | 5 | 0.47424, [ 141 ] 0.4756 [ 142 ] | |
| СК (открыть BC) | 2 | 0.4155 [ 142 ] | |||
| hcp (открытая Британская Колумбия) | 2 | 0.2828 [ 142 ] | |||
| алмаз (открыть до н.э.) | 2 | 0.5451 [ 142 ] | |||
| простой кубический (открытый до н.э.) | 3 | 0.4264 [ 142 ] | |||
| СК (открыть BC) | 3 | 0.3531 [ 142 ] | |||
| bcc (периодический до н.э.) | 3 | 0.21113018(38) [ 143 ] | |||
| hcp (открытая Британская Колумбия) | 3 | 0.2548 [ 142 ] | |||
| алмаз (открыть до н.э.) | 3 | 0.5044 [ 142 ] | |||
| простой кубический (открытый до н.э.) | 4 | 0.3997, [ 141 ] 0.3998 [ 142 ] | |||
| СК (открыть BC) | 4 | 0.3232 [ 142 ] | |||
| bcc (периодический до н.э.) | 4 | 0.20235168(59) [ 143 ] | |||
| hcp (открытая Британская Колумбия) | 4 | 0.2405 [ 142 ] | |||
| алмаз (открыть до н.э.) | 4 | 0.4842 [ 142 ] | |||
| простая кубическая (периодическая до н.э.) | 5 | 6 | 6 | 0.278102(5) [ 143 ] | |
| простой кубический (открытый до н.э.) | 6 | 0.3708 [ 142 ] | |||
| простая кубическая (периодическая до н.э.) | 6 | 6 | 6 | 0.272380(2) [ 143 ] | |
| СК (открыть BC) | 6 | 0.2948 [ 142 ] | |||
| hcp (открытая Британская Колумбия) | 6 | 0.2261 [ 142 ] | |||
| алмаз (открыть до н.э.) | 6 | 0.4642 [ 142 ] | |||
| простая кубическая (периодическая до н.э.) | 7 | 6 | 6 | 0.3459514(12) [ 143 ] | 0.268459(1) [ 143 ] |
| простой кубический (открытый до н.э.) | 8 | 0.3557, [ 141 ] 0.3565 [ 142 ] | |||
| простая кубическая (периодическая до н.э.) | 8 | 6 | 6 | 0.265615(5) [ 143 ] | |
| СК (открыть BC) | 8 | 0.2811 [ 142 ] | |||
| hcp (открытая Британская Колумбия) | 8 | 0.2190 [ 142 ] | |||
| алмаз (открыть до н.э.) | 8 | 0.4549 [ 142 ] | |||
| простой кубический (открытый до н.э.) | 12 | 0.3411 [ 142 ] | |||
| СК (открыть BC) | 12 | 0.2688 [ 142 ] | |||
| hcp (открытая Британская Колумбия) | 12 | 0.2117 [ 142 ] | |||
| алмаз (открыть до н.э.) | 12 | 0.4456 [ 142 ] | |||
| простой кубический (открытый до н.э.) | 16 | 0.3219, [ 141 ] 0.3339 [ 142 ] | |||
| СК (открыть BC) | 16 | 0.2622 [ 142 ] | |||
| hcp (открытая Британская Колумбия) | 16 | 0.2086 [ 142 ] | |||
| алмаз (открыть до н.э.) | 16 | 0.4415 [ 142 ] | |||
| простой кубический (открытый до н.э.) | 32 | 0.3219, [ 141 ] | |||
| простой кубический (открытый до н.э.) | 64 | 0.3165, [ 141 ] | |||
| простой кубический (открытый до н.э.) | 128 | 0.31398, [ 141 ] |
Перколяция в 3D
[ редактировать ]| Решетка | С | коэффициент заполнения* | фракция наполнения* | Порог проникновения сайта | Порог перколяции облигаций | |
|---|---|---|---|---|---|---|
| (10,3)-оксид (или сайт-связь) [ 144 ] | 2 3 3 2 | 2.4 | 0.748713(22) [ 144 ] | = ( p c, связь (10,3) – a ) 1 ⁄ 2 = 0.742334(25) [ 145 ] | ||
| (10,3)-b оксид (или центральная связь) [ 144 ] | 2 3 3 2 | 2.4 | 0.233 [ 146 ] | 0.174 | 0.745317(25) [ 144 ] | = ( p c, связь (10,3) – b ) 1 ⁄ 2 = 0.739388(22) [ 145 ] |
| диоксид кремния (связь с алмазным сайтом) [ 144 ] | 4,2 2 | 2 2 ⁄ 3 | 0.638683(35) [ 144 ] | |||
| Модифицированный (10,3)-б [ 147 ] | 3 2 ,2 | 2 2 ⁄ 3 | 0.627 [ 147 ] | |||
| (8,3)-а [ 145 ] | 3 | 3 | 0.577962(33) [ 145 ] | 0.555700(22) [ 145 ] | ||
| (10,3)-а [ 145 ] гироид [ 148 ] | 3 | 3 | 0.571404(40) [ 145 ] | 0.551060(37) [ 145 ] | ||
| (10,3)-б [ 145 ] | 3 | 3 | 0.565442(40) [ 145 ] | 0.546694(33) [ 145 ] | ||
| кубический оксид (кубическая связь) [ 144 ] | 6,2 3 | 3.5 | 0.524652(50) [ 144 ] | |||
| bcc двойной | 4 | 0.4560(6) [ 149 ] | 0.4031(6) [ 149 ] | |||
| лед, я | 4 | 4 | π √ 3/16 = 0,340087 | 0.147 | 0.433(11) [ 150 ] | 0.388(10) [ 151 ] |
| алмаз (Ледяной Ic) | 4 | 4 | π √ 3/16 = 0,340087 | 0.1462332 | 0.4299(8), [ 152 ] 0.4299870(4), [ 153 ] 0.426 +0.08 −0.02 , [ 154 ] 0.4297(4) [ 155 ] 0.4301(4), [ 156 ] 0.428(4), [ 157 ] 0.425(15), [ 158 ] 0.425, [ 41 ] [ 48 ] 0.436(12) [ 150 ] |
0.3895892(5), [ 153 ] 0.3893(2), [ 156 ] 0.3893(3), [ 155 ] 0.388(5), [ 158 ] 0.3886(5), [ 152 ] 0.388(5) [ 157 ] 0.390(11) [ 151 ] |
| двойной бриллиант | 6 2 ⁄ 3 | 0.3904(5) [ 149 ] | 0.2350(5) [ 149 ] | |||
| 3D кагоме (граф, покрывающий ромбовидную решетку) | 6 | π √ 2/12 = 0,37024 | 0.1442 | 0.3895(2) [ 159 ] =p c (узел) для двойного алмаза и p c (связь) для решетки алмаза [ 149 ] | 0.2709(6) [ 149 ] | |
| Стек галстуков-бабочек двойной | 5 1 ⁄ 3 | 0.3480(4) [ 38 ] | 0.2853(4) [ 38 ] | |||
| сотовый стек | 5 | 5 | 0.3701(2) [ 38 ] | 0.3093(2) [ 38 ] | ||
| восьмиугольный стек двойной | 5 | 5 | 0.3840(4) [ 38 ] | 0.3168(4) [ 38 ] | ||
| пятиугольная стопка | 5 1 ⁄ 3 | 0.3394(4) [ 38 ] | 0.2793(4) [ 38 ] | |||
| стек кагоме | 6 | 6 | 0.453450 | 0.1517 | 0.3346(4) [ 38 ] | 0.2563(2) [ 38 ] |
| двойной FCC | 4 2 ,8 | 5 1 ⁄ 3 | 0.3341(5) [ 149 ] | 0.2703(3) [ 149 ] | ||
| простой кубический | 6 | 6 | π/6 = 0,5235988 | 0.1631574 | 0.307(10), [ 158 ] 0.307, [ 41 ] 0.3115(5), [ 160 ] 0.3116077(2), [ 161 ] 0.311604(6), [ 162 ] 0.311605(5), [ 163 ] 0.311600(5), [ 164 ] 0.3116077(4), [ 165 ] 0.3116081(13), [ 166 ] 0.3116080(4), [ 167 ] 0.3116060(48), [ 168 ] 0.3116004(35), [ 169 ] 0.31160768(15) [ 153 ] | 0.247(5), [ 158 ] 0.2479(4), [ 152 ] 0.2488(2), [ 170 ] 0.24881182(10), [ 161 ] 0.2488125(25), [ 171 ] 0.2488126(5), [ 172 ] |
| hcp двойной | 4 4 ,8 2 | 5 1 ⁄ 3 | 0.3101(5) [ 149 ] | 0.2573(3) [ 149 ] | ||
| стопка кубиков | 5,8 | 6 | π √ 3/9 = 0,604600 | 0.1813 | 0.2998(4) [ 38 ] | 0.2378(4) [ 38 ] |
| стопка галстуков-бабочек | 7 | 7 | 0.2822(6) [ 38 ] | 0.2092(4) [ 38 ] | ||
| Составной треугольный/простой шестиугольный | 8 | 8 | 0.26240(5), [ 173 ] 0.2625(2), [ 174 ] 0.2623(2) [ 38 ] | 0.18602(2), [ 173 ] 0.1859(2) [ 38 ] | ||
| восьмиугольная стопка (Юнион Джек) | 6,10 | 8 | 0.2524(6) [ 38 ] | 0.1752(2) [ 38 ] | ||
| СК | 8 | 8 | 0.243(10), [ 158 ] 0.243, [ 41 ] 0.2459615(10), [ 167 ] 0.2460(3), [ 175 ] 0.2464(7), [ 152 ] 0.2458(2) [ 156 ] | 0.178(5), [ 158 ] 0.1795(3), [ 152 ] 0.18025(15), [ 170 ] 0.1802875(10) [ 172 ] | ||
| простая кубическая форма с 3NN (то же, что и bcc) | 8 | 8 | 0.2455(1), [ 176 ] 0.2457(7) [ 177 ] | |||
| ГЦК, Д 3 | 12 | 12 | π/(3 √ 2 ) = 0,740480 | 0.147530 | 0.195, [ 41 ] 0.198(3), [ 178 ] 0.1998(6), [ 152 ] 0.1992365(10), [ 167 ] 0.19923517(20), [ 153 ] 0.1994(2), [ 156 ] 0.199236(4) [ 179 ] | 0.1198(3), [ 152 ] 0.1201635(10) [ 172 ] 0.120169(2) [ 179 ] |
| ГЦП | 12 | 12 | π/(3 √ 2 ) = 0,740480 | 0.147545 | 0.195(5), [ 158 ] 0.1992555(10) [ 180 ] | 0.1201640(10), [ 180 ] 0.119(2) [ 158 ] |
| La 2−x Sr x CuO 4 | 12 | 12 | 0.19927(2) [ 181 ] | |||
| простая кубическая единица с 2NN (то же, что и fcc) | 12 | 12 | 0.1991(1) [ 176 ] | |||
| простой кубик с NN+4NN | 12 | 12 | 0.15040(12), [ 182 ] 0.1503793(7) [ 183 ] | 0.1068263(7) [ 184 ] | ||
| простой кубик с 3NN+4NN | 14 | 14 | 0.20490(12) [ 182 ] | 0.1012133(7) [ 184 ] | ||
| bcc NN+2NN (= sc(3,4) sc-3NN+4NN) | 14 | 14 | 0.175, [ 41 ] 0.1686,(20) [ 185 ] 0.1759432(8) | 0.0991(5), [ 185 ] 0.1012133(7), [ 45 ] 0.1759432(8) [ 45 ] | ||
| Нанотрубные волокна на FCC | 14 | 14 | 0.1533(13) [ 186 ] | |||
| простой кубик с NN+3NN | 14 | 14 | 0.1420(1) [ 176 ] | 0.0920213(7) [ 184 ] | ||
| простой кубик с 2NN+4NN | 18 | 18 | 0.15950(12) [ 182 ] | 0.0751589(9) [ 184 ] | ||
| простой кубик с NN+2NN | 18 | 18 | 0.137, [ 48 ] 0.136, [ 187 ] 0.1372(1), [ 176 ] 0.13735(5), [ нужна ссылка ] 0.1373045(5) [ 45 ] | 0.0752326(6) [ 184 ] | ||
| fcc с NN+2NN (=sc-2NN+4NN) | 18 | 18 | 0.136, [ 41 ] 0.1361408(8) [ 45 ] | 0.0751589(9) [ 45 ] | ||
| простая кубика с короткой корреляцией | 6+ | 6+ | 0.126(1) [ 188 ] | |||
| простой кубик с NN+3NN+4NN | 20 | 20 | 0.11920(12) [ 182 ] | 0.0624379(9) [ 184 ] | ||
| простой кубик с 2NN+3NN | 20 | 20 | 0.1036(1) [ 176 ] | 0.0629283(7) [ 184 ] | ||
| простой кубик с NN+2NN+4NN | 24 | 24 | 0.11440(12) [ 182 ] | 0.0533056(6) [ 184 ] | ||
| простой кубик с 2NN+3NN+4NN | 26 | 26 | 0.11330(12) [ 182 ] | 0.0474609(9) | ||
| простой кубик с NN+2NN+3NN | 26 | 26 | 0.097, [ 41 ] 0.0976(1), [ 176 ] 0.0976445(10), 0.0976444(6) [ 45 ] | 0.0497080(10) [ 184 ] | ||
| скрытая копия с NN+2NN+3NN | 26 | 26 | 0.095, [ 48 ] 0.0959084(6) [ 45 ] | 0.0492760(10) [ 45 ] | ||
| простой кубик с NN+2NN+3NN+4NN | 32 | 32 | 0.10000(12), [ 182 ] 0.0801171(9) [ 45 ] | 0.0392312(8) [ 184 ] | ||
| ГЦК с NN+2NN+3NN | 42 | 42 | 0.061, [ 48 ] 0.0610(5), [ 187 ] 0.0618842(8) [ 45 ] | 0.0290193(7) [ 45 ] | ||
| ГЦК с NN+2NN+3NN+4NN | 54 | 54 | 0.0500(5) [ 187 ] | |||
| sc-1,2,3,4,5 простая кубическая с NN+2NN+3NN+4NN+5NN | 56 | 56 | 0.0461815(5) [ 45 ] | 0.0210977(7) [ 45 ] | ||
| сбн-1,...,6 (куб 2x2x2 [ 51 ] ) | 80 | 80 | 0.0337049(9), [ 45 ] 0.03373(13) [ 51 ] | 0.0143950(10) [ 45 ] | ||
| ПК-1,...,7 | 92 | 92 | 0.0290800(10) [ 45 ] | 0.0123632(8) [ 45 ] | ||
| ПК-1,...,8 | 122 | 122 | 0.0218686(6) [ 45 ] | 0.0091337(7) [ 45 ] | ||
| ПК-1,...,9 | 146 | 146 | 0.0184060(10) [ 45 ] | 0.0075532(8) [ 45 ] | ||
| ПК-1,...,10 | 170 | 170 | 0.0064352(8) [ 45 ] | |||
| ПК-1,...,11 | 178 | 178 | 0.0061312(8) [ 45 ] | |||
| ПК-1,...,12 | 202 | 202 | 0.0053670(10) [ 45 ] | |||
| ПК-1,...,13 | 250 | 250 | 0.0042962(8) [ 45 ] | |||
| кубик 3х3х3 | 274 | 274 | φ с = 0,76564(1), [ 52 ] р с = 0,0098417(7), [ 52 ] 0.009854(6) [ 51 ] | |||
| Куб 4x4x4 | 636 | 636 | φ с =0,76362(1), [ 52 ] р с = 0,0042050(2), [ 52 ] 0.004217(3) [ 51 ] | |||
| Куб 5х5х5 | 1214 | 1250 | φ с =0,76044(2), [ 52 ] р с = 0,0021885(2), [ 52 ] 0.002185(4) [ 51 ] | |||
| Куб 6x6x6 | 2056 | 2056 | 0.001289(2) [ 51 ] |
Коэффициент заполнения = доля пространства, заполненная соприкасающимися сферами в каждом узле решетки (только для систем с одинаковой длиной связи). Также называется атомным фактором упаковки .
Доля наполнения (или критическая фракция наполнения) = коэффициент наполнения * p c (место установки).
NN = ближайший сосед, 2NN = следующий ближайший сосед, 3NN = следующий ближайший сосед и т. д.
Кубы kxkxk представляют собой кубы занятых мест на решетке и эквивалентны перколяции куба длины (2k+1) с расширенным диапазоном, с удаленными ребрами и углами, с z = (2k+1). 3 -12(2k-1)-9 (центральный участок не учитывается в z).
Вопрос: пороги связи для ГПУ и ГЦК-решетки. согласен в пределах небольшой статистической погрешности. Они идентичны, и если нет, то на каком расстоянии они друг от друга? Какой порог ожидается выше? Аналогично для ледяных и алмазных решеток. Видеть [ 189 ]
| Система | полимер Φ c |
|---|---|
| просачивающийся исключенный объем атермальной полимерной матрицы (модель связи-флуктуации на кубической решетке) | 0.4304(3) [ 190 ] |
3D искаженные решетки
[ редактировать ]Здесь искажается регулярная решетка с единичными интервалами, равномерно перемещая вершины внутри куба. и учитывает просачивание, когда сайты находятся в пределах евклидова расстояния друг друга.
| Решетка | Порог проникновения сайта | Порог перколяции облигаций | |||
|---|---|---|---|---|---|
| кубический | 0.05 | 1.0 | 0.60254(3) [ 191 ] | ||
| 0.1 | 1.00625 | 0.58688(4) [ 191 ] | |||
| 0.15 | 1.025 | 0.55075(2) [ 191 ] | |||
| 0.175 | 1.05 | 0.50645(5) [ 191 ] | |||
| 0.2 | 1.1 | 0.44342(3) [ 191 ] |
Перекрывающиеся фигуры на 3D-решетках
[ редактировать ]Порог узла — это количество перекрывающихся объектов на узел решетки. Покрытие φ c — это чистая доля охваченных сайтов, а v — объем (количество кубов). Перекрывающиеся кубы приведены в разделе о порогах трехмерных решеток. Здесь z — координационное число k-меров любой ориентации, причем
| Система | к | С | Покрытие сайта φ c | Порог проникновения сайта p c |
|---|---|---|---|---|
| 1 х 2 димер, кубическая решетка | 2 | 56 | 0.24542 [ 51 ] | 0.045847(2) [ 51 ] |
| Тример 1 х 3, кубическая решетка | 3 | 104 | 0.19578 [ 51 ] | 0.023919(9) [ 51 ] |
| Палочка 1 х 4, кубическая решетка | 4 | 164 | 0.16055 [ 51 ] | 0.014478(7) [ 51 ] |
| Палочка 1 х 5, кубическая решетка | 5 | 236 | 0.13488 [ 51 ] | 0.009613(8) [ 51 ] |
| Палочка 1 х 6, кубическая решетка | 6 | 320 | 0.11569 [ 51 ] | 0.006807(2) [ 51 ] |
| Плакетка 2 х 2, кубическая решетка | 2 | 0.22710 [ 51 ] | 0.021238(2) [ 51 ] | |
| Плакетка 3 х 3, кубическая решетка | 3 | 0.18686 [ 51 ] | 0.007632(5) [ 51 ] | |
| Плакетка 4 х 4, кубическая решетка | 4 | 0.16159 [ 51 ] | 0.003665(3) [ 51 ] | |
| Плакетка 5 х 5, кубическая решетка | 5 | 0.14316 [ 51 ] | 0.002058(5) [ 51 ] | |
| Плакетка 6 х 6, кубическая решетка | 6 | 0.12900 [ 51 ] | 0.001278(5) [ 51 ] |
Покрытие рассчитывается из к для палочек и для тромбоцитов.
Перколяция димеров в 3D
[ редактировать ]| Система | Порог проникновения сайта | Порог перколяции облигаций |
|---|---|---|
| Простой кубический | 0.2555(1) [ 192 ] |
Пороги для 3D-моделей континуума
[ редактировать ]Все перекрывается, кроме затертых сфер и полимерной матрицы.
| Система | Φ с | η с |
|---|---|---|
| Сферы радиуса r | 0.289, [ 193 ] 0.293, [ 194 ] 0.286, [ 195 ] 0.295. [ 101 ] 0.2895(5), [ 196 ] 0.28955(7), [ 197 ] 0.2896(7), [ 198 ] 0.289573(2), [ 199 ] 0.2896, [ 200 ] 0.2854, [ 201 ] 0.290, [ 202 ] 0.290 [ 203 ] | 0.3418(7), [ 196 ] 0.3438(13), [ 204 ] 0.341889(3), [ 199 ] 0.3360, [ 201 ] 0.34189(2) [ 113 ] [исправлено], 0,341935(8), [ 205 ] 0.335, [ 206 ] |
| Сплющенные эллипсоиды с большим радиусом r и соотношением сторон. 4 ⁄ 3 | 0.2831 [ 201 ] | 0.3328 [ 201 ] |
| Вытянутые эллипсоиды с малым радиусом r и соотношением сторон. 3 ⁄ 2 | 0.2757, [ 200 ] 0.2795, [ 201 ] 0.2763 [ 202 ] | 0.3278 [ 201 ] |
| Сплюснутые эллипсоиды с большим радиусом r и соотношением сторон 2. | 0.2537, [ 200 ] 0.2629, [ 201 ] 0.254 [ 202 ] | 0.3050 [ 201 ] |
| Вытянутые эллипсоиды с малым радиусом r и соотношением сторон 2. | 0.2537, [ 200 ] 0.2618, [ 201 ] 0.25(2), [ 207 ] 0.2507 [ 202 ] | 0.3035, [ 201 ] 0.29(3) [ 207 ] |
| Сплюснутые эллипсоиды с большим радиусом r и соотношением сторон 3. | 0.2289 [ 201 ] | 0.2599 [ 201 ] |
| Вытянутые эллипсоиды с малым радиусом r и соотношением сторон 3. | 0.2033, [ 200 ] 0.2244, [ 201 ] 0.20(2) [ 207 ] | 0.2541, [ 201 ] 0.22(3) [ 207 ] |
| Сплюснутые эллипсоиды с большим радиусом r и соотношением сторон 4. | 0.2003 [ 201 ] | 0.2235 [ 201 ] |
| Вытянутые эллипсоиды с малым радиусом r и соотношением сторон 4. | 0.1901, [ 201 ] 0.16(2) [ 207 ] | 0.2108, [ 201 ] 0.17(3) [ 207 ] |
| Сплюснутые эллипсоиды с большим радиусом r и соотношением сторон 5. | 0.1757 [ 201 ] | 0.1932 [ 201 ] |
| Вытянутые эллипсоиды с малым радиусом r и соотношением сторон 5. | 0.1627, [ 201 ] 0.13(2) [ 207 ] | 0.1776, [ 201 ] 0.15(2) [ 207 ] |
| Сплющенные эллипсоиды с большим радиусом r и соотношением сторон 10. | 0.0895, [ 200 ] 0.1058 [ 201 ] | 0.1118 [ 201 ] |
| Вытянутые эллипсоиды с малым радиусом r и соотношением сторон 10. | 0.0724, [ 200 ] 0.08703, [ 201 ] 0.07(2) [ 207 ] | 0.09105, [ 201 ] 0.07(2) [ 207 ] |
| Сплюснутые эллипсоиды с большим радиусом r и соотношением сторон 100. | 0.01248 [ 201 ] | 0.01256 [ 201 ] |
| Вытянутые эллипсоиды с малым радиусом r и соотношением сторон 100. | 0.006949 [ 201 ] | 0.006973 [ 201 ] |
| Сплюснутые эллипсоиды с большим радиусом r и соотношением сторон 1000. | 0.001275 [ 201 ] | 0.001276 [ 201 ] |
| Сплюснутые эллипсоиды с большим радиусом r и соотношением сторон 2000 г. | 0.000637 [ 201 ] | 0.000637 [ 201 ] |
| Сфероцилиндры с H/D = 1 | 0.2439(2) [ 198 ] | |
| Сфероцилиндры с H/D = 4 | 0.1345(1) [ 198 ] | |
| Сфероцилиндры с H/D = 10 | 0.06418(20) [ 198 ] | |
| Сфероцилиндры с H/D = 50 | 0.01440(8) [ 198 ] | |
| Сфероцилиндры с H/D = 100 | 0.007156(50) [ 198 ] | |
| Сфероцилиндры с H/D = 200 | 0.003724(90) [ 198 ] | |
| Выровненные цилиндры | 0.2819(2) [ 208 ] | 0.3312(1) [ 208 ] |
| Выровненные кубики стороны | 0.2773(2) [ 114 ] 0.27727(2), [ 52 ] 0.27730261(79) [ 168 ] | 0.3247(3), [ 113 ] 0.3248(3), [ 114 ] 0.32476(4) [ 208 ] 0.324766(1) [ 168 ] |
| Случайно ориентированные икосаэдры | 0.3030(5) [ 209 ] | |
| Случайно ориентированные додекаэдры | 0.2949(5) [ 209 ] | |
| Случайно ориентированные октаэдры | 0.2514(6) [ 209 ] | |
| Случайно ориентированные кубики сторон | 0.2168(2) [ 114 ] 0.2174, [ 200 ] | 0.2444(3), [ 114 ] 0.2443(5) [ 209 ] |
| Случайно ориентированные тетраэдры | 0.1701(7) [ 209 ] | |
| Случайно ориентированные диски радиуса r (в 3D) | 0.9614(5) [ 210 ] | |
| Случайно ориентированные квадратные пластины боковых сторон | 0.8647(6) [ 210 ] | |
| Беспорядочно ориентированные треугольные пластины боковых сторон | 0.7295(6) [ 210 ] | |
| Jammed spheres (average z = 6) | 0.183(3),[211] 0.1990,[212] see also contact network of jammed spheres below. | 0.59(1)[211] (volume fraction of all spheres) |
is the total volume (for spheres), where N is the number of objects and L is the system size.
is the critical volume fraction, valid for overlapping randomly placed objects.
For disks and plates, these are effective volumes and volume fractions.
For void ("Swiss-Cheese" model), is the critical void fraction.
For more results on void percolation around ellipsoids and elliptical plates, see.[213]
For more ellipsoid percolation values see.[201]
For spherocylinders, H/D is the ratio of the height to the diameter of the cylinder, which is then capped by hemispheres. Additional values are given in.[198]
For superballs, m is the deformation parameter, the percolation values are given in.,[214][215] In addition, the thresholds of concave-shaped superballs are also determined in [121]
For cuboid-like particles (superellipsoids), m is the deformation parameter, more percolation values are given in.[200]
Void percolation in 3D
[edit]Void percolation refers to percolation in the space around overlapping objects. Here refers to the fraction of the space occupied by the voids (not of the particles) at the critical point, and is related to by . is defined as in the continuum percolation section above.
| System | Φc | ηc |
|---|---|---|
| Voids around disks of radius r | 22.86(2)[213] | |
| Voids around randomly oriented tetrahedra | 0.0605(6)[216] | |
| Voids around oblate ellipsoids of major radius r and aspect ratio 32 | 0.5308(7)[217] | 0.6333[217] |
| Voids around oblate ellipsoids of major radius r and aspect ratio 16 | 0.3248(5)[217] | 1.125[217] |
| Voids around oblate ellipsoids of major radius r and aspect ratio 10 | 1.542(1)[213] | |
| Voids around oblate ellipsoids of major radius r and aspect ratio 8 | 0.1615(4)[217] | 1.823[217] |
| Voids around oblate ellipsoids of major radius r and aspect ratio 4 | 0.0711(2)[217] | 2.643,[217] 2.618(5)[213] |
| Voids around oblate ellipsoids of major radius r and aspect ratio 2 | 3.239(4) [213] | |
| Voids around prolate ellipsoids of aspect ratio 8 | 0.0415(7)[218] | |
| Voids around prolate ellipsoids of aspect ratio 6 | 0.0397(7)[218] | |
| Voids around prolate ellipsoids of aspect ratio 4 | 0.0376(7)[218] | |
| Voids around prolate ellipsoids of aspect ratio 3 | 0.03503(50)[218] | |
| Voids around prolate ellipsoids of aspect ratio 2 | 0.0323(5)[218] | |
| Voids around aligned square prisms of aspect ratio 2 | 0.0379(5) [219] | |
| Voids around randomly oriented square prisms of aspect ratio 20 | 0.0534(4) [219] | |
| Voids around randomly oriented square prisms of aspect ratio 15 | 0.0535(4) [219] | |
| Voids around randomly oriented square prisms of aspect ratio 10 | 0.0524(5) [219] | |
| Voids around randomly oriented square prisms of aspect ratio 8 | 0.0523(6) [219] | |
| Voids around randomly oriented square prisms of aspect ratio 7 | 0.0519(3) [219] | |
| Voids around randomly oriented square prisms of aspect ratio 6 | 0.0519(5) [219] | |
| Voids around randomly oriented square prisms of aspect ratio 5 | 0.0515(7) [219] | |
| Voids around randomly oriented square prisms of aspect ratio 4 | 0.0505(7) [219] | |
| Voids around randomly oriented square prisms of aspect ratio 3 | 0.0485(11) [219] | |
| Voids around randomly oriented square prisms of aspect ratio 5/2 | 0.0483(8) [219] | |
| Voids around randomly oriented square prisms of aspect ratio 2 | 0.0465(7) [219] | |
| Voids around randomly oriented square prisms of aspect ratio 3/2 | 0.0461(14) [219] | |
| Voids around hemispheres | 0.0455(6)[220] | |
| Voids around aligned tetrahedra | 0.0605(6)[216] | |
| Voids around randomly oriented tetrahedra | 0.0605(6)[216] | |
| Voids around aligned cubes | 0.036(1),[52] 0.0381(3)[216] | |
| Voids around randomly oriented cubes | 0.0452(6),[216] 0.0449(5)[219] | |
| Voids around aligned octahedra | 0.0407(3)[216] | |
| Voids around randomly oriented octahedra | 0.0398(5)[216] | |
| Voids around aligned dodecahedra | 0.0356(3)[216] | |
| Voids around randomly oriented dodecahedra | 0.0360(3)[216] | |
| Voids around aligned icosahedra | 0.0346(3)[216] | |
| Voids around randomly oriented icosahedra | 0.0336(7)[216] | |
| Voids around spheres | 0.034(7),[221] 0.032(4),[222] 0.030(2),[119] 0.0301(3),[223] 0.0294,[218] 0.0300(3),[224] 0.0317(4),[225] 0.0308(5)[220] 0.0301(1),[217] 0.0301(1)[216] | 3.506(8),[224] 3.515(6),[213] 3.510(2)[105] |
Thresholds on 3D random and quasi-lattices
[edit]| Lattice | z | Site percolation threshold | Bond percolation threshold | |
|---|---|---|---|---|
| Contact network of packed spheres | 6 | 0.310(5),[211] 0.287(50),[226] 0.3116(3),[212] | ||
| Random-plane tessellation, dual | 6 | 0.290(7)[227] | ||
| Icosahedral Penrose | 6 | 0.285[228] | 0.225[228] | |
| Penrose w/2 diagonals | 6.764 | 0.271[228] | 0.207[228] | |
| Penrose w/8 diagonals | 12.764 | 0.188[228] | 0.111[228] | |
| Voronoi network | 15.54 | 0.1453(20)[185] | 0.0822(50)[185] |
Thresholds for other 3D models
[edit]| Lattice | z | Site percolation threshold | Critical coverage fraction | Bond percolation threshold | |
|---|---|---|---|---|---|
| Drilling percolation, simple cubic lattice* | 6 | 6 | 0.6345(3),[229] 0.6339(5),[230] 0.633965(15)[231] | 0.25480 | |
| Drill in z direction on cubic lattice, remove single sites | 6 | 6 | 0.592746 (columns), 0.4695(10) (sites)[232] | 0.2784 | |
| Random tube model, simple cubic lattice† | 0.231456(6)[233] | ||||
| Pac-Man percolation, simple cubic lattice | 0.139(6)[234] |
In drilling percolation, the site threshold represents the fraction of columns in each direction that have not been removed, and . For the 1d drilling, we have (columns) (sites).
† In tube percolation, the bond threshold represents the value of the parameter such that the probability of putting a bond between neighboring vertical tube segments is , where is the overlap height of two adjacent tube segments.[233]
Thresholds in different dimensional spaces
[edit]Continuum models in higher dimensions
[edit]| d | System | Φc | ηc |
|---|---|---|---|
| 4 | Overlapping hyperspheres | 0.1223(4)[113] | 0.1300(13),[204] 0.1304(5)[113] |
| 4 | Aligned hypercubes | 0.1132(5),[113] 0.1132348(17) [168] | 0.1201(6)[113] |
| 4 | Voids around hyperspheres | 0.00211(2)[120] | 6.161(10)[120] 6.248(2),[105] |
| 5 | Overlapping hyperspheres | 0.0544(6),[204] 0.05443(7)[113] | |
| 5 | Aligned hypercubes | 0.04900(7),[113] 0.0481621(13)[168] | 0.05024(7)[113] |
| 5 | Voids around hyperspheres | 1.26(6)x10−4[120] | 8.98(4),[120] 9.170(8)[105] |
| 6 | Overlapping hyperspheres | 0.02391(31),[204] 0.02339(5)[113] | |
| 6 | Aligned hypercubes | 0.02082(8),[113] 0.0213479(10)[168] | 0.02104(8)[113] |
| 6 | Voids around hyperspheres | 8.0(6)x10−6 [120] | 11.74(8),[120] 12.24(2),[105] |
| 7 | Overlapping hyperspheres | 0.01102(16),[204] 0.01051(3)[113] | |
| 7 | Aligned hypercubes | 0.00999(5),[113] 0.0097754(31)[168] | 0.01004(5)[113] |
| 7 | Voids around hyperspheres | 15.46(5)[105] | |
| 8 | Overlapping hyperspheres | 0.00516(8),[204] 0.004904(6)[113] | |
| 8 | Aligned hypercubes | 0.004498(5)[113] | |
| 8 | Voids around hyperspheres | 18.64(8)[105] | |
| 9 | Overlapping hyperspheres | 0.002353(4)[113] | |
| 9 | Aligned hypercubes | 0.002166(4)[113] | |
| 9 | Voids around hyperspheres | 22.1(4)[105] | |
| 10 | Overlapping hyperspheres | 0.001138(3)[113] | |
| 10 | Aligned hypercubes | 0.001058(4)[113] | |
| 11 | Overlapping hyperspheres | 0.0005530(3)[113] | |
| 11 | Aligned hypercubes | 0.0005160(3)[113] |
In 4d, .
In 5d, .
In 6d, .
is the critical volume fraction, valid for overlapping objects.
For void models, is the critical void fraction, and is the total volume of the overlapping objects
Thresholds on hypercubic lattices
[edit]| d | z | Site thresholds | Bond thresholds |
|---|---|---|---|
| 4 | 8 | 0.198(1)[235] 0.197(6),[236] 0.1968861(14),[237] 0.196889(3),[238] 0.196901(5),[239] 0.19680(23),[240] 0.1968904(65),[168] 0.19688561(3)[241] | 0.1600(1),[242] 0.16005(15),[170] 0.1601314(13),[237] 0.160130(3),[238] 0.1601310(10),[171] 0.1601312(2),[243] 0.16013122(6)[241] |
| 5 | 10 | 0.141(1),0.198(1)[235] 0.141(3),[236] 0.1407966(15),[237] 0.1407966(26),[168] 0.14079633(4)[241] | 0.1181(1),[242] 0.118(1),[244] 0.11819(4),[170] 0.118172(1),[237] 0.1181718(3)[171] 0.11817145(3)[241] |
| 6 | 12 | 0.106(1),[235] 0.108(3),[236] 0.109017(2),[237] 0.1090117(30),[168] 0.109016661(8)[241] | 0.0943(1),[242] 0.0942(1),[245] 0.0942019(6),[237] 0.09420165(2)[241] |
| 7 | 14 | 0.05950(5),[245] 0.088939(20),[246] 0.0889511(9),[237] 0.0889511(90),[168] 0.088951121(1),[241] | 0.0787(1),[242] 0.078685(30),[245] 0.0786752(3),[237] 0.078675230(2)[241] |
| 8 | 16 | 0.0752101(5),[237] 0.075210128(1)[241] | 0.06770(5),[245] 0.06770839(7),[237] 0.0677084181(3)[241] |
| 9 | 18 | 0.0652095(3),[237] 0.0652095348(6)[241] | 0.05950(5),[245] 0.05949601(5),[237] 0.0594960034(1)[241] |
| 10 | 20 | 0.0575930(1),[237] 0.0575929488(4)[241] | 0.05309258(4),[237] 0.0530925842(2)[241] |
| 11 | 22 | 0.05158971(8),[237] 0.0515896843(2)[241] | 0.04794969(1),[237] 0.04794968373(8)[241] |
| 12 | 24 | 0.04673099(6),[237] 0.0467309755(1)[241] | 0.04372386(1),[237] 0.04372385825(10)[241] |
| 13 | 26 | 0.04271508(8),[237] 0.04271507960(10)[241] | 0.04018762(1),[237] 0.04018761703(6)[241] |
For thresholds on high dimensional hypercubic lattices, we have the asymptotic series expansions [236] [244] [247]
where . For 13-dimensional bond percolation, for example, the error with the measured value is less than 10−6, and these formulas can be useful for higher-dimensional systems.
Thresholds in other higher-dimensional lattices
[edit]| d | lattice | z | Site thresholds | Bond thresholds |
|---|---|---|---|---|
| 4 | diamond | 5 | 0.2978(2)[156] | 0.2715(3)[156] |
| 4 | kagome | 8 | 0.2715(3)[159] | 0.177(1) [156] |
| 4 | bcc | 16 | 0.1037(3)[156] | 0.074(1),[156] 0.074212(1)[243] |
| 4 | fcc, D4, hypercubic 2NN | 24 | 0.0842(3),[156] 0.08410(23),[240] 0.0842001(11)[179] | 0.049(1),[156] 0.049517(1),[243] 0.0495193(8)[179] |
| 4 | hypercubic NN+2NN | 32 | 0.06190(23),[240] 0.0617731(19)[248] | 0.035827(1),[243] 0.0338047(27)[248] |
| 4 | hypercubic 3NN | 32 | 0.04540(23)[240] | |
| 4 | hypercubic NN+3NN | 40 | 0.04000(23)[240] | 0.0271892(22)[248] |
| 4 | hypercubic 2NN+3NN | 56 | 0.03310(23)[240] | 0.0194075(15)[248] |
| 4 | hypercubic NN+2NN+3NN | 64 | 0.03190(23),[240] 0.0319407(13)[248] | 0.0171036(11)[248] |
| 4 | hypercubic NN+2NN+3NN+4NN | 88 | 0.0231538(12)[248] | 0.0122088(8)[248] |
| 4 | hypercubic NN+...+5NN | 136 | 0.0147918(12)[248] | 0.0077389(9)[248] |
| 4 | hypercubic NN+...+6NN | 232 | 0.0088400(10)[248] | 0.0044656(11)[248] |
| 4 | hypercubic NN+...+7NN | 296 | 0.0070006(6)[248] | 0.0034812(7)[248] |
| 4 | hypercubic NN+...+8NN | 320 | 0.0064681(9)[248] | 0.0032143(8)[248] |
| 4 | hypercubic NN+...+9NN | 424 | 0.0048301(9)[248] | 0.0024117(7)[248] |
| 5 | diamond | 6 | 0.2252(3)[156] | 0.2084(4)[159] |
| 5 | kagome | 10 | 0.2084(4)[159] | 0.130(2)[156] |
| 5 | bcc | 32 | 0.0446(4)[156] | 0.033(1)[156] |
| 5 | fcc, D5, hypercubic 2NN | 40 | 0.0431(3),[156] 0.0435913(6)[179] | 0.026(2),[156] 0.0271813(2)[179] |
| 5 | hypercubic NN+2NN | 50 | 0.0334(2)[249] | 0.0213(1)[249] |
| 6 | diamond | 7 | 0.1799(5)[156] | 0.1677(7)[159] |
| 6 | kagome | 12 | 0.1677(7)[159] | |
| 6 | fcc, D6 | 60 | 0.0252(5),[156] 0.02602674(12)[179] | 0.01741556(5)[179] |
| 6 | bcc | 64 | 0.0199(5)[156] | |
| 6 | E6[179] | 72 | 0.02194021(14)[179] | 0.01443205(8)[179] |
| 7 | fcc, D7 | 84 | 0.01716730(5)[179] | 0.012217868(13)[179] |
| 7 | E7[179] | 126 | 0.01162306(4)[179] | 0.00808368(2)[179] |
| 8 | fcc, D8 | 112 | 0.01215392(4)[179] | 0.009081804(6)[179] |
| 8 | E8[179] | 240 | 0.00576991(2)[179] | 0.004202070(2)[179] |
| 9 | fcc, D9 | 144 | 0.00905870(2)[179] | 0.007028457(3)[179] |
| 9 | [179] | 272 | 0.00480839(2)[179] | 0.0037006865(11)[179] |
| 10 | fcc, D10 | 180 | 0.007016353(9)[179] | 0.005605579(6)[179] |
| 11 | fcc, D11 | 220 | 0.005597592(4)[179] | 0.004577155(3)[179] |
| 12 | fcc, D12 | 264 | 0.004571339(4)[179] | 0.003808960(2)[179] |
| 13 | fcc, D13 | 312 | 0.003804565(3)[179] | 0.0032197013(14)[179] |
Thresholds in one-dimensional long-range percolation
[edit]
In a one-dimensional chain we establish bonds between distinct sites and with probability decaying as a power-law with an exponent . Percolation occurs[250][251] at a critical value for . The numerically determined percolation thresholds are given by:[252]
| Critical thresholds as a function of .[252] The dotted line is the rigorous lower bound.[250] | ||
| 0.1 | 0.047685(8) | 
|
| 0.2 | 0.093211(16) | |
| 0.3 | 0.140546(17) | |
| 0.4 | 0.193471(15) | |
| 0.5 | 0.25482(5) | |
| 0.6 | 0.327098(6) | |
| 0.7 | 0.413752(14) | |
| 0.8 | 0.521001(14) | |
| 0.9 | 0.66408(7) |
Thresholds on hyperbolic, hierarchical, and tree lattices
[edit]In these lattices there may be two percolation thresholds: the lower threshold is the probability above which infinite clusters appear, and the upper is the probability above which there is a unique infinite cluster.


| Lattice | z | Site percolation threshold | Bond percolation threshold | |||
|---|---|---|---|---|---|---|
| Lower | Upper | Lower | Upper | |||
| {3,7} hyperbolic | 7 | 7 | 0.26931171(7),[255] 0.20[256] | 0.73068829(7),[255] 0.73(2)[256] | 0.20,[257] 0.1993505(5)[255] | 0.37,[257] 0.4694754(8)[255] |
| {3,8} hyperbolic | 8 | 8 | 0.20878618(9)[255] | 0.79121382(9)[255] | 0.1601555(2)[255] | 0.4863559(6)[255] |
| {3,9} hyperbolic | 9 | 9 | 0.1715770(1)[255] | 0.8284230(1)[255] | 0.1355661(4)[255] | 0.4932908(1)[255] |
| {4,5} hyperbolic | 5 | 5 | 0.29890539(6)[255] | 0.8266384(5)[255] | 0.27,[257] 0.2689195(3)[255] | 0.52,[257] 0.6487772(3) [255] |
| {4,6} hyperbolic | 6 | 6 | 0.22330172(3)[255] | 0.87290362(7)[255] | 0.20714787(9)[255] | 0.6610951(2)[255] |
| {4,7} hyperbolic | 7 | 7 | 0.17979594(1)[255] | 0.89897645(3)[255] | 0.17004767(3)[255] | 0.66473420(4)[255] |
| {4,8} hyperbolic | 8 | 8 | 0.151035321(9)[255] | 0.91607962(7)[255] | 0.14467876(3)[255] | 0.66597370(3)[255] |
| {4,9} hyperbolic | 8 | 8 | 0.13045681(3)[255] | 0.92820305(3)[255] | 0.1260724(1)[255] | 0.66641596(2)[255] |
| {5,5} hyperbolic | 5 | 5 | 0.26186660(5)[255] | 0.89883342(7)[255] | 0.263(10),[258] 0.25416087(3)[255] | 0.749(10)[258] 0.74583913(3)[255] |
| {7,3} hyperbolic | 3 | 3 | 0.54710885(10)[255] | 0.8550371(5),[255] 0.86(2)[256] | 0.53,[257] 0.551(10),[258] 0.5305246(8)[255] | 0.72,[257] 0.810(10),[258] 0.8006495(5)[255] |
| {∞,3} Cayley tree | 3 | 3 | 1⁄2 | 1⁄2[257] | 1[257] | |
| Enhanced binary tree (EBT) | 0.304(1),[259] 0.306(10),[258] (√13 − 3)/2 = 0.302776[260] | 0.48,[257] 0.564(1),[259] 0.564(10),[258] 1⁄2[260] | ||||
| Enhanced binary tree dual | 0.436(1),[259] 0.452(10)[258] | 0.696(1),[259] 0.699(10)[258] | ||||
| Non-Planar Hanoi Network (HN-NP) | 0.319445[254] | 0.381996[254] | ||||
| Cayley tree with grandparents | 8 | 0.158656326[261] | ||||
Note: {m,n} is the Schläfli symbol, signifying a hyperbolic lattice in which n regular m-gons meet at every vertex
For bond percolation on {P,Q}, we have by duality . For site percolation, because of the self-matching of triangulated lattices.
Cayley tree (Bethe lattice) with coordination number
Thresholds for directed percolation
[edit]

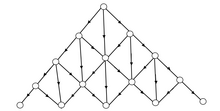
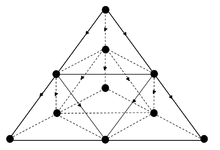

| Lattice | z | Site percolation threshold | Bond percolation threshold |
|---|---|---|---|
| (1+1)-d honeycomb | 1.5 | 0.8399316(2),[262] 0.839933(5),[263] of (1+1)-d sq. | 0.8228569(2),[262] 0.82285680(6)[262] |
| (1+1)-d kagome | 2 | 0.7369317(2),[262] 0.73693182(4)[264] | 0.6589689(2),[262] 0.65896910(8)[262] |
| (1+1)-d square, diagonal | 2 | 0.705489(4),[265] 0.705489(4),[266] 0.70548522(4),[267] 0.70548515(20),[264] 0.7054852(3),[262] | 0.644701(2),[268] 0.644701(1),[269] 0.644701(1),[265] 0.6447006(10),[263] 0.64470015(5),[270] 0.644700185(5),[267] 0.6447001(2),[262] 0.643(2)[271] |
| (1+1)-d triangular | 3 | 0.595646(3),[265] 0.5956468(5),[270] 0.5956470(3)[262] | 0.478018(2),[265] 0.478025(1),[270] 0.4780250(4)[262] 0.479(3)[271] |
| (2+1)-d simple cubic, diagonal planes | 3 | 0.43531(1),[272] 0.43531411(10)[262] | 0.382223(7),[272] 0.38222462(6)[262] 0.383(3)[271] |
| (2+1)-d square nn (= bcc) | 4 | 0.3445736(3),[273] 0.344575(15)[274] 0.3445740(2)[262] | 0.2873383(1),[275] 0.287338(3)[272] 0.28733838(4)[262] 0.287(3)[271] |
| (2+1)-d fcc | 0.199(2))[271] | ||
| (3+1)-d hypercubic, diagonal | 4 | 0.3025(10),[276] 0.30339538(5) [262] | 0.26835628(5),[262] 0.2682(2)[271] |
| (3+1)-d cubic, nn | 6 | 0.2081040(4)[273] | 0.1774970(5)[171] |
| (3+1)-d bcc | 8 | 0.160950(30),[274] 0.16096128(3)[262] | 0.13237417(2)[262] |
| (4+1)-d hypercubic, diagonal | 5 | 0.23104686(3)[262] | 0.20791816(2),[262] 0.2085(2)[271] |
| (4+1)-d hypercubic, nn | 8 | 0.1461593(2),[273] 0.1461582(3)[277] | 0.1288557(5)[171] |
| (4+1)-d bcc | 16 | 0.075582(17),[274] 0.0755850(3),[277] 0.07558515(1)[262] | 0.063763395(5)[262] |
| (5+1)-d hypercubic, diagonal | 6 | 0.18651358(2)[262] | 0.170615155(5),[262] 0.1714(1) [271] |
| (5+1)-d hypercubic, nn | 10 | 0.1123373(2)[273] | 0.1016796(5)[171] |
| (5+1)-d hypercubic bcc | 32 | 0.035967(23),[274] 0.035972540(3)[262] | 0.0314566318(5)[262] |
| (6+1)-d hypercubic, diagonal | 7 | 0.15654718(1)[262] | 0.145089946(3),[262] 0.1458[271] |
| (6+1)-d hypercubic, nn | 12 | 0.0913087(2)[273] | 0.0841997(14)[171] |
| (6+1)-d hypercubic bcc | 64 | 0.017333051(2)[262] | 0.01565938296(10)[262] |
| (7+1)-d hypercubic, diagonal | 8 | 0.135004176(10)[262] | 0.126387509(3),[262] 0.1270(1) [271] |
| (7+1)-d hypercubic,nn | 14 | 0.07699336(7)[273] | 0.07195(5)[171] |
| (7+1)-d bcc | 128 | 0.008 432 989(2)[262] | 0.007 818 371 82(6)[262] |
nn = nearest neighbors. For a (d + 1)-dimensional hypercubic system, the hypercube is in d dimensions and the time direction points to the 2D nearest neighbors.
Directed percolation with multiple neighbors
[edit]| Lattice | z | Site percolation threshold | Bond percolation threshold |
|---|---|---|---|
| (1+1)-d square with 3 NN | 3 | 0.4395(3),[278] |
Site-Bond Directed Percolation
[edit]p_b = bond threshold
p_s = site threshold
Site-bond percolation is equivalent to having different probabilities of connections:
P_0 = probability that no sites are connected
P_2 = probability that exactly one descendant is connected to the upper vertex (two connected together)
P_3 = probability that both descendants are connected to the original vertex (all three connected together)
Formulas:
P_0 = (1-p_s) + p_s(1-p_b)^2
P_2 = p_s p_b (1-p_b)
P_3 = p_s p_b^2
P_0 + 2P_2 + P_3 = 1
| Lattice | z | p_s | p_b | P_0 | P_2 | P_3 |
|---|---|---|---|---|---|---|
| (1+1)-d square [279] | 3 | 0.644701 | 1 | 0.126237 | 0.229062 | 0.415639 |
| 0.7 | 0.93585 | 0.148376 | 0.196529 | 0.458567 | ||
| 0.75 | 0.88565 | 0.169703 | 0.166059 | 0.498178 | ||
| 0.8 | 0.84135 | 0.192304 | 0.134616 | 0.538464 | ||
| 0.85 | 0.80190 | 0.216143 | 0.102242 | 0.579373 | ||
| 0.9 | 0.76645 | 0.241215 | 0.068981 | 0.620825 | ||
| 0.95 | 0.73450 | 0.267336 | 0.034889 | 0.662886 | ||
| 1 | 0.705489 | 0.294511 | 0 | 0.705489 |
Exact critical manifolds of inhomogeneous systems
[edit]Inhomogeneous triangular lattice bond percolation[20]
Inhomogeneous honeycomb lattice bond percolation = kagome lattice site percolation[20]
Inhomogeneous (3,12^2) lattice, site percolation[7][280]
or
Inhomogeneous union-jack lattice, site percolation with probabilities [281]
Inhomogeneous martini lattice, bond percolation[73][282]
Inhomogeneous martini lattice, site percolation. r = site in the star
Inhomogeneous martini-A (3–7) lattice, bond percolation. Left side (top of "A" to bottom): . Right side: . Cross bond: .
Inhomogeneous martini-B (3–5) lattice, bond percolation
Inhomogeneous martini lattice with outside enclosing triangle of bonds, probabilities from inside to outside, bond percolation[282]
Inhomogeneous checkerboard lattice, bond percolation[57][93]
Inhomogeneous bow-tie lattice, bond percolation[56][93]
where are the four bonds around the square and is the diagonal bond connecting the vertex between bonds and .
See also
[edit]References
[edit]- ^ Stauffer, Dietrich; Aharony, Amnon (2003). Introduction to percolation theory (Rev. 2nd ed.). London: Taylor & Francis. ISBN 978-0-7484-0253-3.
- ^ Kasteleyn, P. W.; Fortuin, C. M. (1969). "Phase transitions in lattice systems with random local properties". Journal of the Physical Society of Japan Supplement. 26: 11–14. Bibcode:1969JPSJS..26...11K.
- ^ Jump up to: a b c d e Grünbaum, Branko & Shephard, G. C. (1987). Tilings and Patterns. New York: W. H. Freeman. ISBN 978-0-7167-1193-3.
- ^ Berchenko, Yakir; Artzy-Randrup, Yael; Teicher, Mina; Stone, Lewi (March 30, 2009). "Emergence and Size of the Giant Component in Clustered Random Graphs with a Given Degree Distribution". Physical Review Letters. 102 (13): 138701. Bibcode:2009PhRvL.102m8701B. doi:10.1103/PhysRevLett.102.138701. ISSN 0031-9007. PMID 19392410.
- ^ Li, Ming; Liu, Run-Ran; Lü, Linyuan; Hu, Mao-Bin; Xu, Shuqi; Zhang, Yi-Cheng (April 25, 2021). "Percolation on complex networks: Theory and application". Physics Reports. 907: 1–68. arXiv:2101.11761. Bibcode:2021PhR...907....1L. doi:10.1016/j.physrep.2020.12.003. ISSN 0370-1573. S2CID 231719831.
- ^ Jump up to: a b c d e f g Parviainen, Robert (2005). Connectivity Properties of Archimedean and Laves Lattices. Vol. 34. Uppsala Dissertations in Mathematics. p. 37. ISBN 978-91-506-1751-1.
- ^ Jump up to: a b c d e f g h i Suding, P. N.; R. M. Ziff (1999). "Site percolation thresholds for Archimedean lattices". Physical Review E. 60 (1): 275–283. Bibcode:1999PhRvE..60..275S. doi:10.1103/PhysRevE.60.275. PMID 11969760.
- ^ Jump up to: a b c d e f g Parviainen, Robert (2007). "Estimation of bond percolation thresholds on the Archimedean lattices". Journal of Physics A. 40 (31): 9253–9258. arXiv:0704.2098. Bibcode:2007JPhA...40.9253P. doi:10.1088/1751-8113/40/31/005. S2CID 680787.
- ^ Jump up to: a b c d e f g h i Ding, Chengxiang; Zhe Fu. Wenan Guo; F. Y. Wu (2010). "Critical frontier for the Potts and percolation models on triangular-type and kagome-type lattices II: Numerical analysis". Physical Review E. 81 (6): 061111. arXiv:1001.1488. Bibcode:2010PhRvE..81f1111D. doi:10.1103/PhysRevE.81.061111. PMID 20866382. S2CID 29625353.
- ^ Jump up to: a b Scullard, C. R.; J. L. Jacobsen (2012). "Transfer matrix computation of generalised critical polynomials in percolation". arXiv:1209.1451 [cond-mat.stat-mech].
- ^ Jump up to: a b c d e f g h i j k l m n o p q r s t u v Jacobsen, J. L. (2014). "High-precision percolation thresholds and Potts-model critical manifolds from graph polynomials". Journal of Physics A. 47 (13): 135001. arXiv:1401.7847. Bibcode:2014JPhA...47m5001G. doi:10.1088/1751-8113/47/13/135001. S2CID 119614758.
- ^ Jump up to: a b Jacobsen, Jesper L.; Christian R. Scullard (2013). "Critical manifolds, graph polynomials, and exact solvability" (PDF). StatPhys 25, Seoul, Korea July 21–26.
- ^ Jump up to: a b c d e f g h Scullard, Christian R.; Jesper Lykke Jacobsen (2020). "Bond percolation thresholds on Archimedean lattices from critical polynomial roots". Physical Review Research. 2 (1): 012050. arXiv:1910.12376. Bibcode:2020PhRvR...2a2050S. doi:10.1103/PhysRevResearch.2.012050. S2CID 204904858.
- ^ Jump up to: a b c d e d'Iribarne, C.; Rasigni, M.; Rasigni, G. (1995). "Determination of site percolation transitions for 2D mosaics by means of the minimal spanning tree approach". Physics Letters A. 209 (1–2): 95–98. Bibcode:1995PhLA..209...95D. doi:10.1016/0375-9601(95)00794-8.
- ^ Jump up to: a b c d e f g h i j d'Iribarne, C.; Rasigni, M.; Rasigni, G. (1999). "From lattice long-range percolation to the continuum one". Phys. Lett. A. 263 (1–2): 65–69. Bibcode:1999PhLA..263...65D. doi:10.1016/S0375-9601(99)00585-X.
- ^ Jump up to: a b Schliecker, G.; C. Kaiser (1999). "Percolation on disordered mosaics". Physica A. 269 (2–4): 189–200. Bibcode:1999PhyA..269..189S. doi:10.1016/S0378-4371(99)00093-X.
- ^ Djordjevic, Z. V.; H. E. Stanley; Alla Margolina (1982). "Site percolation threshold for honeycomb and square lattices". Journal of Physics A. 15 (8): L405–L412. Bibcode:1982JPhA...15L.405D. doi:10.1088/0305-4470/15/8/006.
- ^ Jump up to: a b c d e Feng, Xiaomei; Youjin Deng; H. W. J. Blöte (2008). "Percolation transitions in two dimensions". Physical Review E. 78 (3): 031136. arXiv:0901.1370. Bibcode:2008PhRvE..78c1136F. doi:10.1103/PhysRevE.78.031136. PMID 18851022. S2CID 29282598.
- ^ Jump up to: a b c d e f g Ziff, R. M.; Hang Gu (2008). "Universal condition for critical percolation thresholds of kagomé-like lattices". Physical Review E. 79 (2): 020102. arXiv:0812.0181. doi:10.1103/PhysRevE.79.020102. PMID 19391694. S2CID 18051122.
- ^ Jump up to: a b c d e Sykes, M. F.; J. W. Essam (1964). "Exact critical percolation probabilities for site and bond problems in two dimensions". Journal of Mathematical Physics. 5 (8): 1117–1127. Bibcode:1964JMP.....5.1117S. doi:10.1063/1.1704215.
- ^ Ziff, R. M.; P. W. Suding (1997). "Determination of the bond percolation threshold for the kagome lattice". Journal of Physics A. 30 (15): 5351–5359. arXiv:cond-mat/9707110. Bibcode:1997JPhA...30.5351Z. doi:10.1088/0305-4470/30/15/021. S2CID 28814369.
- ^ Scullard, C. R. (2012). "Percolation critical polynomial as a graph invariant". Physical Review E. 86 (4): 1131. arXiv:1111.1061. Bibcode:2012PhRvE..86d1131S. doi:10.1103/PhysRevE.86.041131. PMID 23214553. S2CID 33348328.
- ^ Jump up to: a b Jacobsen, J. L. (2015). "Critical points of Potts and O(N) models from eigenvalue identities in periodic Temperley-Lieb algebras". Journal of Physics A. 48 (45): 454003. arXiv:1507.03027. Bibcode:2015JPhA...48S4003L. doi:10.1088/1751-8113/48/45/454003. S2CID 119146630.
- ^ Lin, Keh Ying; Wen Jong Ma (1983). "Two-dimensional Ising model on a ruby lattice". Journal of Physics A. 16 (16): 3895–3898. Bibcode:1983JPhA...16.3895L. doi:10.1088/0305-4470/16/16/027.
- ^ Derrida, B.; D. Stauffer (1985). "Corrections to scaling and phenomenological renormalization for 2-dimensional percolation and lattice animal problems" (PDF). Journal de Physique. 46 (45): 1623. doi:10.1051/jphys:0198500460100162300. S2CID 8289499.
- ^ Yang, Y.; S. Zhou.; Y. Li. (2013). "Square++: Making a connection game win-lose complementary and playing-fair". Entertainment Computing. 4 (2): 105–113. doi:10.1016/j.entcom.2012.10.004.
- ^ Newman, M. E. J.; R. M. Ziff (2000). "Efficient Monte-Carlo algorithm and high-precision results for percolation". Physical Review Letters. 85 (19): 4104–7. arXiv:cond-mat/0005264. Bibcode:2000PhRvL..85.4104N. CiteSeerX 10.1.1.310.4632. doi:10.1103/PhysRevLett.85.4104. PMID 11056635. S2CID 747665.
- ^ Mertens, Stephan (2022). "Exact site-percolation probability on the square lattice". Journal of Physics A: Mathematical and Theoretical. 55 (33): 334002. arXiv:2109.12102. Bibcode:2022JPhA...55G4002M. doi:10.1088/1751-8121/ac4195. ISSN 1751-8113.
- ^ de Oliveira, P.M.C.; R. A. Nobrega; D. Stauffer (2003). "Corrections to finite size scaling in percolation". Brazilian Journal of Physics. 33 (3): 616–618. arXiv:cond-mat/0308525. Bibcode:2003BrJPh..33..616O. doi:10.1590/S0103-97332003000300025. S2CID 8972025.
- ^ Lee, M. J. (2007). "Complementary algorithms for graphs and percolation". Physical Review E. 76 (2): 027702. arXiv:0708.0600. Bibcode:2007PhRvE..76b7702L. doi:10.1103/PhysRevE.76.027702. PMID 17930184. S2CID 304257.
- ^ Lee, M. J. (2008). "Pseudo-random-number generators and the square site percolation threshold". Physical Review E. 78 (3): 031131. arXiv:0807.1576. Bibcode:2008PhRvE..78c1131L. doi:10.1103/PhysRevE.78.031131. PMID 18851017. S2CID 7027694.
- ^ Levenshteĭn, M. E.; B. I. Shklovskiĭ; M. S. Shur; A. L. Éfros (1975). "The relation between the critical exponents of percolation theory". Zh. Eksp. Teor. Fiz. 69: 386–392. Bibcode:1975JETP...42..197L.
- ^ Дин, П.; Н. Ф. Берд (1967). «Оценки критических вероятностей просачивания по методу Монте-Карло». Учеб. Кэмб. Фил. Соц . 63 (2): 477–479. Бибкод : 1967PCPS...63..477D . дои : 10.1017/s0305004100041438 . S2CID 137386357 .
- ^ Дин, П. (1963). «Новый метод Монте-Карло для решения задач перколяции на решетке». Учеб. Кэмб. Фил. Соц . 59 (2): 397–410. Бибкод : 1963PCPS...59..397D . дои : 10.1017/s0305004100037026 . S2CID 122985645 .
- ^ Тенсер, Джон; Форсберг, Келси Микс (2021). «Методы постобработки для прогнозирования перколяции градиента на квадратной решетке». Физ. Преподобный Е. 103 (1): 012115. Бибкод : 2021PhRvE.103a2115T . дои : 10.1103/PhysRevE.103.012115 . ОСТИ 1778027 . ПМИД 33601521 . S2CID 231961701 .
- ^ Беттс, Д.Д. (1995). «Новая двумерная решетка координационного числа пять» . Учеб. Новошотландский инст. Наука . 40 : 95–100. hdl : 10222/35332 .
- ^ Jump up to: а б д'Ирибарн, К.; Расиньи, М.; Расиньи, Г. (1999). «Минимальное остовное дерево и просачивание мозаики: теория графов и протекание». Дж. Физ. А: Математика. Ген . 32 (14): 2611–2622. Бибкод : 1999JPhA...32.2611D . дои : 10.1088/0305-4470/32/14/002 .
- ^ Jump up to: а б с д и ж г час я дж к л м н тот п д р с т в v В ван дер Марк, Стивен С. (1997). «Пороги перколяции и универсальные формулы». Физический обзор E . 55 (2): 1514–1517. Бибкод : 1997PhRvE..55.1514V . дои : 10.1103/PhysRevE.55.1514 .
- ^ Jump up to: а б с д и ж Маларц, К.; С. Галам (2005). «Просачивание узлов квадратной решетки при увеличении дальности соседних связей». Физический обзор E . 71 (1): 016125. arXiv : cond-mat/0408338 . Бибкод : 2005PhRvE..71a6125M . дои : 10.1103/PhysRevE.71.016125 . ПМИД 15697676 . S2CID 119087463 .
- ^ Jump up to: а б с д и ж г час я дж к л м н тот п д р с т в v В х и С аа Маевский, М.; К. Маларц (2007). «Пороги перколяции узлов квадратной решетки для сложных окрестностей». Акта Физ. Пол. Б. 38 (38): 2191. arXiv : cond-mat/0609635 . Бибкод : 2007AcPPB..38.2191M .
- ^ Jump up to: а б с д и ж г час я дж Далтон, Северо-Запад; К. Домб; М. Ф. Сайкс (1964). «Зависимость критической концентрации разбавленного ферромагнетика от области взаимодействия». Учеб. Физ. Соц . 83 (3): 496–498. дои : 10.1088/0370-1328/83/3/118 .
- ^ Кольер, Эндрю. «Порог перколяции: включая ближайших соседей» .
- ^ Jump up to: а б с д и ж г час я дж к л м н Оуян, Юньцин; Ю. Дэн; Хенк В.Дж. Блёте (2018). «Модели перколяции эквивалентных соседей в двух измерениях: пересечение между поведением среднего поля и поведением ближнего действия». Физ. Преподобный Е. 98 (6): 062101. arXiv : 1808.05812 . Бибкод : 2018PhRvE..98f2101O . дои : 10.1103/PhysRevE.98.062101 . S2CID 119328197 .
- ^ Jump up to: а б Сюй, Вэньхуэй; Цзюньфэн Ван; Хао Ху; Юджин Дэн (2021). «Критические полиномы в неплоских и континуальных моделях перколяции». Физический обзор E . 103 (2): 022127. arXiv : 2010.02887 . Бибкод : 2021PhRvE.103b2127X . дои : 10.1103/PhysRevE.103.022127 . ISSN 2470-0045 . ПМИД 33736116 . S2CID 222140792 .
- ^ Jump up to: а б с д и ж г час я дж к л м н тот п д р с т в v В х и С Сюнь, Чжипен; ДаПэн Хао; Роберт М. Зифф (2022). «Пороги перколяции узлов и связей на регулярных решетках с компактными окрестностями расширенного радиуса действия в двух и трех измерениях». Физ. Преподобный Е. 105 (2): 024105. arXiv : 2111.10975 . Бибкод : 2022PhRvE.105b4105X . дои : 10.1103/PhysRevE.105.024105 . ПМИД 35291074 . S2CID 244478657 .
- ^ Jump up to: а б с д и ж г Маларц, Кшиштоп (2021). «Пороги перколяции на треугольной решетке для окрестностей, содержащих узлы до пятой координационной зоны». Физический обзор E . 103 (5): 052107. arXiv : 2102.10066 . Бибкод : 2021PhRvE.103e2107M . дои : 10.1103/PhysRevE.103.052107 . ПМИД 34134312 . S2CID 231979514 .
- ^ Jump up to: а б с д и ж г Маларц, Кшиштоф (2020). «Пороги перколяции узлов на треугольной решетке с комплексными окрестностями». Хаос: междисциплинарный журнал нелинейной науки . 30 (12): 123123. arXiv : 2006.15621 . Бибкод : 2020Хаос..30л3123М . дои : 10.1063/5.0022336 . ПМИД 33380057 . S2CID 220250058 .
- ^ Jump up to: а б с д и ж Домб, К.; С. В. Далтон (1966). «Кристаллическая статистика с дальнодействующими силами I. Модель эквивалентного соседа». Учеб. Физ. Соц . 89 (4): 859–871. Бибкод : 1966PPS....89..859D . дои : 10.1088/0370-1328/89/4/311 .
- ^ Jump up to: а б с д и Гукер, Марк; Семья, Ферейдун (1983). «Доказательства классического критического поведения при просачивании сайтов на большие расстояния». Физ. Преподобный Б. 28 (3): 1449. Бибкод : 1983PhRvB..28.1449G . дои : 10.1103/PhysRevB.28.1449 .
- ^ Маларц, Кшиштоф (2022). «Случайное просачивание узлов на сотовых решетках со сложными окрестностями». Хаос: междисциплинарный журнал нелинейной науки . 32 (8): 083123. arXiv : 2204.12593 . дои : 10.1063/5.0099066 . ПМИД 36049902 . S2CID 248405741 .
- ^ Jump up to: а б с д и ж г час я дж к л м н тот п д р с т в v В х и С аа аб и объявление но из в ах есть также и аль являюсь а к ап ак Мекке, КР; Сейфрид, А. (2002). «Сильная зависимость порогов перколяции от полидисперсности». Письма по еврофизике (EPL) . 58 (1): 28–34. Бибкод : 2002EL.....58...28M . дои : 10.1209/epl/i2002-00601-y . S2CID 250737562 .
- ^ Jump up to: а б с д и ж г час я дж к л м н тот п д р с т в v В Коза, Збигнев; Кондрат, Гжегож; Сущинский, Кароль (2014). «Просачивание перекрывающихся квадратов или кубов на решетке». Журнал статистической механики: теория и эксперимент . 2014 (11): P11005. arXiv : 1606.07969 . Бибкод : 2014JSMTE..11..005K . дои : 10.1088/1742-5468/2014/11/P11005 . S2CID 118623466 .
- ^ Jump up to: а б с Дэн, Юджин; Юньцин Оуян; Хенк В.Дж. Блёте (2019). «Просачивание средней дальности в двух измерениях» . Ж. Физ.: Конф. Сер . 1163 (1): 012001. Бибкод : 2019JPhCS1163a2001D . дои : 10.1088/1742-6596/1163/1/012001 . hdl : 1887/82550 .
- ^ Jump up to: а б с Митра, С.; Д. Саха; А. Сеншарма (2019). «Просачивание в искаженной квадратной решетке». Физ. Преподобный Е. 99 (1): 012117.arXiv : 1808.10665 . Бибкод : 2019PhRvE..99a2117M . дои : 10.1103/PhysRevE.99.012117 . ПМИД 30780325 .
- ^ Jump up to: а б с д и ж Ясна, СК; В. Сасидеван (2023). «Влияние асимметрии формы на просачивание выровненных и перекрывающихся объектов на решетках». Препринт . arXiv : 2308.12932 .
- ^ Jump up to: а б с д Скаллард, ЧР; Р.М. Зифф (2010). «Критические поверхности для общих задач перколяции неоднородных связей». Журнал статистической механики: теория и эксперимент . 2010 (3): P03021. arXiv : 0911.2686 . Бибкод : 2010JSMTE..03..021S . дои : 10.1088/1742-5468/2010/03/P03021 . S2CID 119230786 .
- ^ Jump up to: а б Ву, ФЮ (1979). «Критическая точка плоских моделей Поттса». Журнал физики C. 12 (17): Л645–Л650. Бибкод : 1979JPhC...12L.645W . дои : 10.1088/0022-3719/17.12.002 .
- ^ Jump up to: а б Май, Т.; Галлей, JW (1980). Синха, СК (ред.). Заказ в двух измерениях . Северная Голландия, Амстердам. стр. 369–371.
- ^ Jump up to: а б с д и ж г час я дж Кунду, Суманта; Манна, СС (15 мая 2017 г.). «Цветное перколяция» . Физический обзор E . 95 (5). arXiv : 1709.00887 . дои : 10.1103/PhysRevE.95.052124 . ISSN 2470-0045 .
- ^ Наканиси, Х (1987). «Критическое поведение перколяции AB в двух измерениях» . Журнал физики A: Математический и общий . 20 (17): 6075–6083. дои : 10.1088/0305-4470/20/17/040 . ISSN 0305-4470 .
- ^ Дебьер, Ж-М; Брэдли, РМ (1992). «Масштабные свойства антиперколяционных оболочек на треугольной решетке» . Журнал физики A: Математический и общий . 25 (2): 335–343. дои : 10.1088/0305-4470/25/2/014 . ISSN 0305-4470 .
- ^ У, Сянь-Юань; Попов, С.Ю. (2003). «О перколяции связи AB на квадратной решетке и перколяции узла AB на ее линейном графике» . Журнал статистической физики . 110 (1/2): 443–449. дои : 10.1023/А:1021091316925 .
- ^ Jump up to: а б с д и ж г Хови, Ж.-П.; А. Ахарони (1996). «Масштабирование и универсальность охвата вероятности просачивания». Физический обзор E . 53 (1): 235–253. Бибкод : 1996PhRvE..53..235H . дои : 10.1103/PhysRevE.53.235 . ПМИД 9964253 .
- ^ Jump up to: а б с д и ж г час я дж к л м н тот п д р с Тарасевич Юрий Ю; Стивен К. ван дер Марк (1999). «Исследование просачивания межсайтовых связей на многих решетках». Межд. Дж. Мод. Физ. С. 10 (7): 1193–1204. arXiv : cond-mat/9906078 . Бибкод : 1999IJMPC..10.1193T . дои : 10.1142/S0129183199000978 . S2CID 16917458 .
- ^ Jump up to: а б с д и ж г час я дж Гонсалес-Флорес, Мичиган; А.А. Торрес; В. Лебрехт; Эй Джей Рамирес-Пастор (2021). «Перколяция межсайтовых связей в двумерных решетках кагоме: аналитический подход и численное моделирование». Физ. Преподобный Е. 104 (1): 014130. Бибкод : 2021PhRvE.104a4130G . дои : 10.1103/PhysRevE.104.014130 . ПМИД 34412224 . S2CID 237243188 .
- ^ Jump up to: а б с д и Сакамото, С.; Ф. Ёнезава; М. Хори (1989). «Предложение по оценке порогов перколяции в двумерных решетках». Дж. Физ. А. 22 (14): Л699–Л704. Бибкод : 1989JPhA...22L.699S . дои : 10.1088/0305-4470/22/14/009 .
- ^ Дэн, Ю.; Ю. Хуан; Дж. Л. Якобсен; Дж. Салас; А.Д. Сокаль (2011). «Фазовый переход при конечной температуре в классе антиферромагнетиков Поттса с четырьмя состояниями». Письма о физических отзывах . 107 (15): 150601. arXiv : 1108.1743 . Бибкод : 2011PhRvL.107o0601D . doi : 10.1103/PhysRevLett.107.150601 . ПМИД 22107278 . S2CID 31777818 .
- ^ Сёзи, Я (1972). «Трансформация моделей Изинга». В Домбе, К.; Грин, М.С. (ред.). Фазовые переходы в критических явлениях . Том. 1. Академик Пресс, Лондон. стр. 270–329.
- ^ Jump up to: а б с д и ж г час я дж к л м н тот п д р с т в Неер, Ричард; Мекке, Клаус; Вагнер, Герберт (2008). «Топологическая оценка порогов перколяции». Журнал статистической механики: теория и эксперимент . 2008 (1): P01011. arXiv : 0708.3250 . Бибкод : 2008JSMTE..01..011N . дои : 10.1088/1742-5468/2008/01/P01011 . S2CID 8584164 .
- ^ Гриметт, Г.; Манолеску, я (2012). «Просачивание связей на изорадиальных графах: критичность и универсальность». Теория вероятностей и смежные области . 159 (1–2): 273–327. arXiv : 1204.0505 . дои : 10.1007/s00440-013-0507-y . S2CID 15031903 .
- ^ Jump up to: а б Скаллард, ЧР (2006). «Точные пороги перколяции сайтов с использованием преобразования сайт-связь и преобразования звезда-треугольник». Физический обзор E . 73 (1): 016107. arXiv : cond-mat/0507392 . Бибкод : 2006PhRvE..73a6107S . дои : 10.1103/PhysRevE.73.016107 . ПМИД 16486216 . S2CID 17948429 .
- ^ Jump up to: а б с д Зифф, РМ (2006). «Обобщенная трансформация клетка-двойная клетка и точные пороги перколяции». Физический обзор E . 73 (1): 016134. Бибкод : 2006PhRvE..73a6134Z . дои : 10.1103/PhysRevE.73.016134 . ПМИД 16486243 .
- ^ Jump up to: а б с д и ж г час я дж к л м Скаллард, ЧР; Роберт М. Зифф (2006). «Точные пороги перколяции связей в двух измерениях». Журнал физики А. 39 (49): 15083–15090. arXiv : cond-mat/0610813 . Бибкод : 2006JPhA...3915083Z . дои : 10.1088/0305-4470/39/49/003 . S2CID 14332146 .
- ^ Дин, Чэнсян; Яньчэн Ван; Ян Ли (2012). «Горшки и модели перколяции на решетках-бабочках». Физический обзор E . 86 (2): 021125.arXiv : 1203.2244 . Бибкод : 2012PhRvE..86b1125D . дои : 10.1103/PhysRevE.86.021125 . ПМИД 23005740 . S2CID 27190130 .
- ^ Виерман, Джон (1984). «Определение критической вероятности перколяции связи на основе преобразования звезда-треугольник». Дж. Физ. А: Математика. Ген . 17 (7): 1525–1530. Бибкод : 1984JPhA...17.1525W . дои : 10.1088/0305-4470/17/7/020 .
- ^ Махмуд Махер ан-Накш (1983). «МАХ 007» . Дизайн и выполнение рисунков иранской плитки . Архивировано из оригинала 9 января 2017 года . Проверено 18 ноября 2019 г.
- ^ «Западная башня-гробница Харракан» .
- ^ Jump up to: а б с д и ж г час я дж к л м н Мельхерт, Оливер; Хельмут Г. Кацграбер; Марк А. Новотный (2016). «Пороги перколяции сайтов и связей в решетках на основе Kn,n: уязвимость квантовых отжигателей к случайным отказам кубитов и соединителей в топологиях Химеры». Физический обзор E . 93 (4): 042128. arXiv : 1511.07078 . Бибкод : 2016PhRvE..93d2128M . дои : 10.1103/PhysRevE.93.042128 . ПМИД 27176275 . S2CID 206249608 .
- ^ Окубо, С.; М. Хаяси; С. Кимура; Х. Охта; М. Мотокава; Х. Кикучи; Х. Нагасава (1998). «Субмиллиметровое ЭПР антиферромагнетика треугольного кагоме Cu9X2(cpa)6 (X=Cl, Br)». Физика Б. 246–247 (2): 553–556. Бибкод : 1998PhyB..246..553O . дои : 10.1016/S0921-4526(97)00985-X .
- ^ Jump up to: а б с д и ж г час я дж к Хаджи Акбари, эмир; Р.М. Зифф (2009). «Просачивание в сетях с пустотами и узкими местами». Физический обзор E . 79 (2): 021118.arXiv : 0811.4575 . Бибкод : 2009PhRvE..79b1118H . дои : 10.1103/PhysRevE.79.021118 . ПМИД 19391717 . S2CID 2554311 .
- ^ Jump up to: а б Корнетт, В.; Эй Джей Рамирес-Пастор; Ф. Ньето (2003). «Зависимость порога перколяции от размера просачивающихся частиц». Физика А. 327 (1): 71–75. Бибкод : 2003PhyA..327...71C . дои : 10.1016/S0378-4371(03)00453-9 . hdl : 11336/138178 .
- ^ Jump up to: а б с Лебрехт, В.; Центры ПМ; Эй Джей Рамирес-Пастор (2019). «Аналитическая аппроксимация порогов перколяции сайтов мономеров и димеров на двумерных решетках». Физика А. 516 : 133–143. Бибкод : 2019PhyA..516..133L . дои : 10.1016/j.physa.2018.10.023 . S2CID 125418069 .
- ^ Jump up to: а б с д и ж г час я Лонгоне, Пабло; Центры ПМ; Эй Джей Рамирес-Пастор (2019). «Просачивание соосных жестких стержней на двумерных треугольных решетках». Физический обзор E . 100 (5): 052104. arXiv : 1906.03966 . Бибкод : 2019PhRvE.100e2104L . дои : 10.1103/PhysRevE.100.052104 . ПМИД 31870027 . S2CID 182953009 .
- ^ Jump up to: а б с д Будински-Петкович, Lj; И. Лонкаревич; З.М. Ячик; С.Б. Врховац (2016). «Застревание и перколяция при случайно-последовательной адсорбции протяженных объектов на треугольной решетке с закаленными примесями». Журнал статистической механики: теория и эксперимент . 2016 (5): 053101. Бибкод : 2016JSMTE..05.3101B . дои : 10.1088/1742-5468/2016/05/053101 . S2CID 3913989 .
- ^ Jump up to: а б Черкасова В.А.; Ю. Ю. Тарасевич; Н.И. Лебовка; Н. В. Выгорницкий (2010). «Перколяция выровненных димеров на квадратной решетке». Евро. Физ. Дж . Б. 74 (2): 205–209. arXiv : 0912.0778 . Бибкод : 2010EPJB...74..205C . дои : 10.1140/epjb/e2010-00089-2 . S2CID 118485353 .
- ^ Jump up to: а б с д Леройер, Ю.; Э. Помье (1994). «Анализ Монте-Карло просачивания отрезков прямых на квадратную решетку». Физ. Преподобный Б. 50 (5): 2795–2799. arXiv : cond-mat/9312066 . Бибкод : 1994PhRvB..50.2795L . дои : 10.1103/PhysRevB.50.2795 . ПМИД 9976520 . S2CID 119495907 .
- ^ Jump up to: а б с д и ж г Вандервалле, Н.; С. Галам; М. Крамер (2000). «Новая универсальность для случайного последовательного размещения игл». Евро. Физ. Дж . Б. 14 (3): 407–410. arXiv : cond-mat/0004271 . Бибкод : 2000EPJB...14..407V . дои : 10.1007/s100510051047 . S2CID 11142384 .
- ^ Кондрат, Гжегож; Анджей Пенкальский (2001). «Просачивание и застревание при случайной последовательной адсорбции линейных сегментов на квадратной решетке». Физ. Преподобный Е. 63 (5): 051108. arXiv : cond-mat/0102031 . Бибкод : 2001PhRvE..63e1108K . дои : 10.1103/PhysRevE.63.051108 . ПМИД 11414888 . S2CID 44490067 .
- ^ Jump up to: а б с д и ж г Хаджи-Акбари, А.; Насим Хаджи-Акбари; Роберт М. Зифф (2015). «Димерное покрытие и нарушение перколяции». Физ. Преподобный Е. 92 (3): 032134. arXiv : 1507.04411 . Бибкод : 2015PhRvE..92c2134H . дои : 10.1103/PhysRevE.92.032134 . ПМИД 26465453 . S2CID 34100812 .
- ^ Зия, РКП; В. Йонг; Б. Шмитманн (2009). «Просачивание набора конечных случайных блужданий: модель проникновения газа через тонкие полимерные мембраны». Журнал математической химии . 45 : 58–64. дои : 10.1007/s10910-008-9367-6 . S2CID 94092783 .
- ^ Jump up to: а б с д Ву, Юн; Б. Шмитман ; РКП Зия (2008). «Двумерные полимерные сети вблизи перколяции». Журнал физики А. 41 (2): 025008. Бибкод : 2008JPhA...41b5004W . дои : 10.1088/1751-8113/41/2/025004 . S2CID 13053653 .
- ^ Jump up to: а б с д и ж г час я дж к л м н тот п д р с т в v В х и С аа аб и объявление Корнетт, В.; Эй Джей Рамирес-Пастор; Ф. Ньето (2003). «Просачивание многоатомных частиц по квадратной решетке». Европейский физический журнал Б. 36 (3): 391–399. Бибкод : 2003EPJB...36..391C . дои : 10.1140/epjb/e2003-00358-1 . S2CID 119852589 .
- ^ Jump up to: а б с Зифф, РМ; Ч.Р. Скаллард; Дж. К. Виерман; МРА Седлок (2012). «Критические многообразия просачивания неоднородных связей на решетках в виде галстука-бабочки и шахматной доски». Журнал физики А. 45 (49): 494005. arXiv : 1210.6609 . Бибкод : 2012JPhA...45W4005Z . дои : 10.1088/1751-8113/45/49/494005 . S2CID 2121370 .
- ^ Jump up to: а б с д и ж г час я дж к Мертенс, Стефан; Кристофер Мур (2012). «Пороги перколяции континуума в двух измерениях». Физический обзор E . 86 (6): 061109. arXiv : 1209.4936 . Бибкод : 2012PhRvE..86f1109M . дои : 10.1103/PhysRevE.86.061109 . ПМИД 23367895 . S2CID 15107275 .
- ^ Jump up to: а б с д Кинтанилья, Джон А.; Р. М. Зифф (2007). «Асимметрия порогов перколяции полностью проницаемых дисков с двумя разными радиусами». Физический обзор E . 76 (5): 051115 [6 страниц]. Бибкод : 2007PhRvE..76e1115Q . дои : 10.1103/PhysRevE.76.051115 . ПМИД 18233631 .
- ^ Jump up to: а б с Кинтанилья, Дж; С. Торквато; Р. М. Зифф (2000). «Эффективное измерение порога перколяции для полностью проницаемых дисков». Дж. Физ. А: Математика. Ген . 33 (42): Л399–Л407. Бибкод : 2000JPhA...33L.399Q . CiteSeerX 10.1.1.6.8207 . дои : 10.1088/0305-4470/33/42/104 .
- ^ Лоренц, Б; И. Оргзал; Х.-О. Хойер (1993). «Универсальность и кластерные структуры в континуальных моделях перколяции с двумя разными распределениями радиусов». Дж. Физ. А: Математика. Ген . 26 (18): 4711–4712. Бибкод : 1993JPhA...26.4711L . дои : 10.1088/0305-4470/26/18/032 .
- ^ Россо, М (1989). «Градиентный подход к просачиванию континуума в двух измерениях». Дж. Физ. А: Математика. Ген . 22 (4): Л131–Л136. Бибкод : 1989JPhA...22L.131R . дои : 10.1088/0305-4470/22/4/004 .
- ^ Jump up to: а б Гавлински, Эдвард Т; Х. Юджин Стэнли (1981). «Просачивание континуума в двух измерениях: тесты Монте-Карло на масштабирование и универсальность для невзаимодействующих дисков». Дж. Физ. А: Математика. Ген . 14 (8): Л291–Л299. Бибкод : 1981JPhA...14L.291G . дои : 10.1088/0305-4470/14/8/007 .
- ^ Jump up to: а б с д и ж г час я дж к л м н тот п д р Йи, Ю.-Б.; А. М. Састри (2004). «Аналитическая аппроксимация порога перколяции для перекрывающихся эллипсоидов вращения». Труды Королевского общества А. 460 (5): 2353–2380. Бибкод : 2004RSPSA.460.2353Y . дои : 10.1098/rspa.2004.1279 . S2CID 2475482 .
- ^ Jump up to: а б с Пайк, GE; CH Сигер (1974). «Перколяция и проводимость: компьютерное исследование I». Физ. Преподобный Б. 10 (4): 1421–1434. Бибкод : 1974PhRvB..10.1421P . дои : 10.1103/PhysRevB.10.1421 .
- ^ Jump up to: а б с д и ж г час я дж к Линь, Цзяньцзюнь; Чен, Хуэйсу (2019). «Измерение свойств перколяции континуума двумерных систем частиц, включающих конгруэнтные и бинарные суперэллипсы». Порошковая технология . 347 : 17–26. дои : 10.1016/j.powtec.2019.02.036 . S2CID 104332397 .
- ^ Ли, Минци; Чен, Хуэйсу; Линь, Цзяньцзюнь; Чжан, Жунлин; Лю, Линь (июль 2021 г.). «Влияние полидисперсности формы пор на порог перколяции и диффузионную способность пористых композитов: теоретические и численные исследования» . Порошковая технология . 386 : 382–393. дои : 10.1016/j.powtec.2021.03.055 . ISSN 0032-5910 . S2CID 233675695 .
- ^ Коза, Збигнев; Петр Бжески; Гжегож Кондрат (2023). «Просачивание полностью проницаемых дисков методом трехногого кластера» . Дж. Физ. А: Математика. Теор . (в печати) (16): 165001. Бибкод : 2023JPhA...56p5001K . дои : 10.1088/1751-8121/acc3d0 . S2CID 257524315 .
- ^ Jump up to: а б с д и ж г час Шарбоно, Бенуа; Патрик Шарбонно; И Ху; Чжэнь Ян (2021). «Высокоразмерная критичность перколяции и намеки на клетку случайного газа Лоренца, подобную среднему полю». Физ. Преподобный Е. 104 (2): 024137. arXiv : 2105.04711 . Бибкод : 2021PhRvE.104b4137C . дои : 10.1103/PhysRevE.104.024137 . ПМИД 34525662 . S2CID 234357912 .
- ^ Гилберт, EN (1961). «Случайные плоские сети». Дж. Сок. Промышленность. Прил. Математика . 9 (4): 533–543. дои : 10.1137/0109045 .
- ^ Сюй, Вэньхуэй; Цзюньфэн Ван; Хао Ху; Юджин Дэн (2021). «Критические полиномы в неплоских и континуальных моделях перколяции». Физический обзор E . 103 (2): 022127. arXiv : 2010.02887 . Бибкод : 2021PhRvE.103b2127X . дои : 10.1103/PhysRevE.103.022127 . ISSN 2470-0045 . ПМИД 33736116 . S2CID 222140792 .
- ^ Jump up to: а б с Тарасевич Юрий Ю.; Андрей В. Есеркепов (2020). «Пороги перколяции для дископрямоугольников: численная оценка для диапазона соотношений сторон». Физический обзор E . 101 (2): 022108. arXiv : 1910.05072 . Бибкод : 2020PhRvE.101b2108T . дои : 10.1103/PhysRevE.101.022108 . ПМИД 32168641 . S2CID 204401814 .
- ^ Jump up to: а б с д и ж г час я дж к л м н тот п д р с Ли, Цзяньтун; Микаэль Эстлинг (2016). «Точные пороги перколяции двумерных случайных систем, состоящих из перекрывающихся эллипсов» . Физика А. 462 : 940–950. Бибкод : 2016PhyA..462..940L . дои : 10.1016/j.physa.2016.06.020 .
- ^ Нгуен, Ван Лиен; Энрике Канесса (1999). «Масштабирование конечного размера в двумерных моделях перколяции континуума». Буквы современной физики Б. 13 (17): 577–583. arXiv : cond-mat/9909200 . Бибкод : 1999MPLB...13..577N . дои : 10.1142/S0217984999000737 . S2CID 18560722 .
- ^ Робертс, ФДК (1967). «Решение Монте-Карло двумерной неструктурированной кластерной задачи». Биометрика . 54 (3/4): 625–628. дои : 10.2307/2335053 . JSTOR 2335053 . ПМИД 6064024 .
- ^ Jump up to: а б с д и ж г час я дж к л м н тот п д р с т в Ся, В.; М. Ф. Торп (1988). «Свойства перколяции случайных эллипсов». Физический обзор А. 38 (5): 2650–2656. Бибкод : 1988PhRvA..38.2650X . дои : 10.1103/PhysRevA.38.2650 . ПМИД 9900674 .
- ^ Jump up to: а б с д и ж г час я дж к л м н тот п д р с т в v В х и С Торквато, С.; Ю. Цзяо (2012). «Влияние размерности на просачивание континуума перекрывающихся гиперсфер и гиперкубов. II. Результаты моделирования и анализа». Дж. Хим. Физ . 137 (7): 074106. arXiv : 1208.3720 . Бибкод : 2012JChPh.137g4106T . дои : 10.1063/1.4742750 . ПМИД 22920102 . S2CID 13188197 .
- ^ Jump up to: а б с д и ж г час я дж к л Бейкер, Дон Р.; Джеральд Пол; Самит Шринивасан; Х. Юджин Стэнли (2002). «Порог перколяции континуума для взаимопроникающих квадратов и кубов». Физический обзор E . 66 (4): 046136 [5 страниц]. arXiv : cond-mat/0203235 . Бибкод : 2002PhRvE..66d6136B . дои : 10.1103/PhysRevE.66.046136 . ПМИД 12443288 . S2CID 9561586 .
- ^ Jump up to: а б с д и ж г час я дж к л м н тот Ли, Цзяньтун; Микаэль Эстлинг (2013). «Пороги перколяции двумерных континуальных систем прямоугольников» . Физический обзор E . 88 (1): 012101. Бибкод : 2013PhRvE..88a2101L . дои : 10.1103/PhysRevE.88.012101 . ПМИД 23944408 . S2CID 21438506 .
- ^ Ли, Цзяньтун; Ши-Ли Чжан (2009). «Масштабирование конечного размера при перколяции палочек». Физический обзор E . 80 (4): 040104(Р). Бибкод : 2009PhRvE..80d0104L . дои : 10.1103/PhysRevE.80.040104 . ПМИД 19905260 .
- ^ Jump up to: а б с Тарасевич Юрий Ю.; Андрей В. Есеркепов (2018). «Просачивание палочек: влияние выравнивания палочек и дисперсии длины». Физический обзор E . 98 (6): 062142. arXiv : 1811.06681 . Бибкод : 2018PhRvE..98f2142T . дои : 10.1103/PhysRevE.98.062142 . S2CID 54187951 .
- ^ Jump up to: а б с д и ж г час я Сасидеван, В. (2013). «Континуальная просачивание перекрывающихся дисков с распределением радиусов, имеющим степенной хвост». Физический обзор E . 88 (2): 022140.arXiv : 1302.0085 . Бибкод : 2013PhRvE..88b2140S . дои : 10.1103/PhysRevE.88.022140 . ПМИД 24032808 . S2CID 24046421 .
- ^ Jump up to: а б ван дер Марк, Стивен С. (1996). «Сетевой подход к просачиванию пустот в пакете неравных сфер». Письма о физических отзывах . 77 (9): 1785–1788. Бибкод : 1996PhRvL..77.1785V . doi : 10.1103/PhysRevLett.77.1785 . ПМИД 10063171 .
- ^ Jump up to: а б с д и ж г Цзинь, Юлян; Патрик Шарбонно (2014). «Сопоставление остановки случайного газа Лоренца с динамическим переходом простого стеклообразователя». Физический обзор E . 91 (4): 042313. arXiv : 1409.0688 . Бибкод : 2015PhRvE..91d2313J . дои : 10.1103/PhysRevE.91.042313 . ПМИД 25974497 . S2CID 16117644 .
- ^ Jump up to: а б Линь, Цзяньцзюнь; Чжан, Улун; Чен, Хуэйсу; Чжан, Жунлин; Лю, Линь (2019). «Влияние характеристик пор на порог перколяции и коэффициент диффузии пористой среды, содержащей перекрывающиеся поры вогнутой формы». Международный журнал тепломассообмена . 138 : 1333–1345. doi : 10.1016/j.ijheatmasstransfer.2019.04.110 . S2CID 164424008 .
- ^ Микс, Келси; Дж. Тенсер; М.Л. Пантойя (2017). «Просачивание бинарных дисковых систем: моделирование и теория» . Физ. Преподобный Е. 95 (1): 012118. Бибкод : 2017PhRvE..95a2118M . дои : 10.1103/PhysRevE.95.012118 . ПМИД 28208494 .
- ^ Кинтанилья, Джон А. (2001). «Измерение порога перколяции для полностью проницаемых дисков разного радиуса». Физ. Преподобный Е. 63 (6): 061108. Бибкод : 2001PhRvE..63f1108Q . дои : 10.1103/PhysRevE.63.061108 . ПМИД 11415069 .
- ^ Jump up to: а б с Мельчерт, Оливер (2013). «Пороги перколяции на плоских евклидовых графах относительной окрестности». Физический обзор E . 87 (4): 042106. arXiv : 1301.6967 . Бибкод : 2013PhRvE..87d2106M . дои : 10.1103/PhysRevE.87.042106 . ПМИД 23679372 . S2CID 9691279 .
- ^ Jump up to: а б Бернарди, Оливье; Курьен, Николя; Мирмонт, Грегори (2019). «Больцмановский подход к просачиванию случайных триангуляций». Канадский математический журнал . 71 : 1–43. arXiv : 1705.04064 . дои : 10.4153/CJM-2018-009-x . S2CID 6817693 .
- ^ Jump up to: а б с д и Беккер, А.; Р.М. Зифф (2009). «Пороги перколяции в двумерных сетях Вороного и триангуляциях Делоне». Физический обзор E . 80 (4): 041101. arXiv : 0906.4360 . Бибкод : 2009PhRvE..80d1101B . дои : 10.1103/PhysRevE.80.041101 . ПМИД 19905267 . S2CID 22549508 .
- ^ Шанте, Канзас; С. Киркпатрик (1971). «Введение в теорию перколяции». Достижения физики . 20 (85): 325–357. Бибкод : 1971AdPhy..20..325S . дои : 10.1080/00018737100101261 .
- ^ Jump up to: а б с Сюй, HP; MC Хуан (1999). «Пороги перколяции, критические показатели и масштабирующие функции на плоских случайных решетках и их двойственных решетках». Физический обзор E . 60 (6): 6361–6370. Бибкод : 1999PhRvE..60.6361H . дои : 10.1103/PhysRevE.60.6361 . ПМИД 11970550 . S2CID 8750738 .
- ^ Jump up to: а б Хуанг, Мин-Чанг; Сяо-Пин Сюй (2002). «Пороги перколяции, критические показатели и масштабирующие функции на сферических случайных решетках». Международный журнал современной физики C . 13 (3): 383–395. дои : 10.1142/S012918310200319X .
- ^ Jump up to: а б Норренброк, К. (2014). «Порог перколяции на плоских евклидовых графах Габриэля». Журнал физики А. 40 (31): 9253–9258. arXiv : 0704.2098 . Бибкод : 2007JPhA...40.9253P . дои : 10.1088/1751-8113/40/31/005 . S2CID 680787 .
- ^ Jump up to: а б Бертен, Э; Ж.-М. Биллиот; Р. Друйе (2002). «Просачивание континуума в графе Габриэля». Адв. Прил. Вероятно . 34 (4): 689. doi : 10.1239/aap/1037990948 . S2CID 121288601 .
- ^ Лепаж, Тибо; Люси Делаби; Фаусто Мальваги; Ален Маццоло (2011). «Моделирование Монте-Карло полностью марковской стохастической геометрии» . Прогресс ядерной науки и технологий . 2 : 743–748. дои : 10.15669/pnst.2.743 .
- ^ Чжан, К.; К. Де'Белл (1993). «Переформулировка задачи перколяции на квазирешетке: оценки порога перколяции, химической размерности и отношения амплитуд». Физ. Преподобный Б. 47 (14): 8558–8564. Бибкод : 1993PhRvB..47.8558Z . дои : 10.1103/PhysRevB.47.8558 . ПМИД 10004894 .
- ^ Зифф, РМ; Ф. Бабалиевский (1999). «Просачивание узлов на ромбовидной решетке Пенроуза». Физика А. 269 (2–4): 201–210. Бибкод : 1999PhyA..269..201Z . дои : 10.1016/S0378-4371(99)00166-1 .
- ^ Лу, Цзянь Пин; Джозеф Л. Бирман (1987). «Просачивание и масштабирование на квазирешетке». Журнал статистической физики . 46 (5/6): 1057–1066. Бибкод : 1987JSP....46.1057L . дои : 10.1007/BF01011156 . S2CID 121645524 .
- ^ Jump up to: а б с д и ж г час Бабалиевский, Ф. (1995). «Пороги перколяции и перколяционная проводимость октагональных и додекагональных квазикристаллических решеток». Физика А. 220 (1995): 245–250. Бибкод : 1995PhyA..220..245B . дои : 10.1016/0378-4371(95)00260-E .
- ^ Боллобас, Бела; Оливер Риордан (2006). «Критическая вероятность случайной перколяции Вороного в плоскости равна 1/2». Вероятно. Теория Отн. Поля . 136 (3): 417–468. arXiv : math/0410336 . дои : 10.1007/s00440-005-0490-z . S2CID 15985691 .
- ^ Ангел, Омер; Шрамм, Одед (2003). «Равномерная бесконечная плоская триангуляция». Коммун. Математика. Физ . 241 (2–3): 191–213. arXiv : math/0207153 . Бибкод : 2003CMaPh.241..191A . дои : 10.1007/s00220-003-0932-3 . S2CID 17718301 .
- ^ Ангел.; Курьен, Николя (2014). «Просачивание на случайных картах I: модели полуплоскости». Анналы Института Анри Пуанкаре, Вероятности и статистики . 51 (2): 405–431. arXiv : 1301.5311 . Бибкод : 2015AIHPB..51..405A . дои : 10.1214/13-AIHP583 . S2CID 14964345 .
- ^ Jump up to: а б с Циренберг, Йоханнес; Никлас Фрике; Мартин Маренц; Ф.П. Шпицнер; Виктория Блаватская; Вольфхард Янке (2017). «Пороги перколяции и фрактальные размерности для квадратных и кубических решеток с дальнодействующими коррелированными дефектами». Физ. Преподобный Е. 96 (6): 062125.arXiv : 1708.02296 . Бибкод : 2017PhRvE..96f2125Z . дои : 10.1103/PhysRevE.96.062125 . ПМИД 29347311 . S2CID 22353394 .
- ^ Jump up to: а б с д и ж г Сотта, П.; Д. Лонг (2003). «Переход от 2D к 3D перколяции: теория и численное моделирование». Евро. Физ. Дж . Э. 11 (4): 375–388. Бибкод : 2003EPJE...11..375S . дои : 10.1140/epje/i2002-10161-6 . ПМИД 15011039 . S2CID 32831742 .
- ^ Jump up to: а б с д и ж г час я дж к л м н тот п д р с т в v В х и С аа аб Хортон, МК; Морам, Массачусетс (17 апреля 2017 г.). «Флуктуации состава сплава и перколяция в квантовых ямах полупроводниковых сплавов». Письма по прикладной физике . 110 (16): 162103. Бибкод : 2017ApPhL.110p2103H . дои : 10.1063/1.4980089 . ISSN 0003-6951 .
- ^ Jump up to: а б с д и ж г Глиоцци, Ф.; С. Лоттини; М. Панеро; А. Раго (2005). «Случайная перколяция как калибровочная теория». Ядерная физика Б . 719 (3): 255–274. arXiv : cond-mat/0502339 . Бибкод : 2005НуФБ.719..255Г . doi : 10.1016/j.nuclphysb.2005.04.021 . hdl : 2318/5995 . S2CID 119360708 .
- ^ Jump up to: а б с д и ж г час Йоу, Тед Ю.; Джонатан Тран; Шейн П. Сталхебер; Карина Э. Кааиноа; Кевин Джепанг; Александр Р. Смолл (2014). «Просачивание сайтов на решетках с низкими средними координационными числами». Журнал статистической механики: теория и эксперимент . 2014 (6): P06014. arXiv : 1403.1676 . Бибкод : 2014JSMTE..06..014Y . дои : 10.1088/1742-5468/2014/06/p06014 . S2CID 119290405 .
- ^ Jump up to: а б с д и ж г час я дж к Тран, Джонатан; Тед Ю; Шейн Сталхебер; Алекс Смолл (2013). «Пороги перколяции на трехмерных решетках с тремя ближайшими соседями». Журнал статистической механики: теория и эксперимент . 2013 (5): P05014. arXiv : 1211.6531 . Бибкод : 2013JSMTE..05..014T . дои : 10.1088/1742-5468/2013/05/P05014 . S2CID 119182062 .
- ^ Уэллс, А. Ф. (1984). «Структуры на основе 3-связной сети 10 3 – б ». Журнал «Химия твердого тела» . 54 (3): 378–388. Бибкод : 1984JSSCh..54..378W . doi : 10.1016/0022-4596(84)90169-5 .
- ^ Jump up to: а б Пант, Михир; Дон Таусли; Дирк Инглунд; Сайкат Гуха (2017). «Пороги перколяции для фотонных квантовых вычислений» . Природные коммуникации . 10 (1): 1070. arXiv : 1701.03775 . дои : 10.1038/s41467-019-08948-x . ПМК 6403388 . ПМИД 30842425 .
- ^ Хайд, Стивен Т.; О'Киф, Майкл; Прозерпио, Давиде М. (2008). «Краткая история неуловимой, но повсеместной структуры в химии, материалах и математике». Энджью. хим. Межд. Эд . 47 (42): 7996–8000. дои : 10.1002/anie.200801519 . ПМИД 18767088 .
- ^ Jump up to: а б с д и ж г час я дж ван дер Марк, Стивен С. (1997). «Пороги перколяции двойников гранецентрированно-кубической, гексагонально-плотноупакованной и алмазной решеток». Физ. Преподобный Е. 55 (6): 6593–6597. Бибкод : 1997PhRvE..55.6593V . дои : 10.1103/PhysRevE.55.6593 .
- ^ Jump up to: а б Фриш, Х.Л.; Э. Зонненблик; В.А. Высоцкий; Дж. М. Хаммерсли (1961). «Критические вероятности перколяции (проблема сайта)». Физический обзор . 124 (4): 1021–1022. Бибкод : 1961PhRv..124.1021F . дои : 10.1103/PhysRev.124.1021 .
- ^ Jump up to: а б Высоцкий, В.А.; С.Б. Гордон; Х. Л. Фриш; Дж. М. Хаммерсли (1961). «Критические вероятности перколяции (проблема облигаций)». Физический обзор . 123 (5): 1566–1567. Бибкод : 1961PhRv..123.1566V . дои : 10.1103/PhysRev.123.1566 .
- ^ Jump up to: а б с д и ж г Гонт, Д.С.; М. Ф. Сайкс (1983). «Серийное исследование случайной перколяции в трех измерениях». Дж. Физ. А. 16 (4): 783. Бибкод : 1983JPhA...16..783G . дои : 10.1088/0305-4470/16/4/016 .
- ^ Jump up to: а б с д Сюй, Сяо; Цзюньфэн Ван; Цзянь-Пин Лев; Юджин Дэн (2014). «Одновременный анализ трехмерных моделей перколяции». Границы физики . 9 (1): 113–119. arXiv : 1310.5399 . Бибкод : 2014FrPhy...9..113X . дои : 10.1007/s11467-013-0403-z . S2CID 119250232 .
- ^ Сильверман, Амихал; Дж. Адлер (1990). «Порог перколяции сайтов для алмазной решетки с двухатомным замещением». Физический обзор B . 42 (2): 1369–1373. Бибкод : 1990PhRvB..42.1369S . дои : 10.1103/PhysRevB.42.1369 . ПМИД 9995550 .
- ^ Jump up to: а б ван дер Марк, Стивен С. (1997). «Ошибка: пороги перколяции и универсальные формулы [Phys. Rev. E 55, 1514 (1997)]» . Физ. Преподобный Е. 56 (3): 3732. Бибкод : 1997PhRvE..56.3732V . дои : 10.1103/PhysRevE.56.3732.2 .
- ^ Jump up to: а б с д и ж г час я дж к л м н тот п д р с т ван дер Марк, Стивен С. (1998). «Расчет порогов перколяции в больших размерностях для FCC, BCC и ромбовидных решеток». Международный журнал современной физики C . 9 (4): 529–540. arXiv : cond-mat/9802187 . Бибкод : 1998IJMPC...9..529В . дои : 10.1142/S0129183198000431 . S2CID 119097158 .
- ^ Jump up to: а б Сайкс, МФ; Д.С. Гонт; М. Глен (1976). «Процессы перколяции в трех измерениях». Дж. Физ. А: Математика. Ген . 9 (10): 1705–1712. Бибкод : 1976JPhA....9.1705S . дои : 10.1088/0305-4470/10.09.021 .
- ^ Jump up to: а б с д и ж г час Сайкс, МФ; Дж. В. Эссам (1964). «Критические вероятности перколяции методом серий». Физический обзор . 133 (1А): А310–А315. Бибкод : 1964PhRv..133..310S . дои : 10.1103/PhysRev.133.A310 .
- ^ Jump up to: а б с д и ж ван дер Марк, Стивен С. (1998). «Просачивание сайтов и случайные блуждания на d-мерных решетках Кагоме». Журнал физики А. 31 (15): 3449–3460. arXiv : cond-mat/9801112 . Бибкод : 1998JPhA...31.3449V . дои : 10.1088/0305-4470/31/15/010 . S2CID 18989583 .
- ^ Сур, Амит; Джоэл Л. Лебовиц; Дж. Марро; М. Х. Калос; С. Киркпатрик (1976). «Исследование явлений перколяции методом Монте-Карло для простой кубической решетки». Журнал статистической физики . 15 (5): 345–353. Бибкод : 1976JSP....15..345S . дои : 10.1007/BF01020338 . S2CID 38734613 .
- ^ Jump up to: а б Ван, Дж; З. Чжоу; В. Чжан; Т. Гарони; Ю. Дэн (2013). «Связь и просачивание сайтов в трех измерениях». Физический обзор E . 87 (5): 052107.arXiv : 1302.0421 . Бибкод : 2013PhRvE..87e2107W . дои : 10.1103/PhysRevE.87.052107 . ПМИД 23767487 . S2CID 14087496 .
- ^ Грассбергер, П. (1992). «Численные исследования критической перколяции в трех измерениях». Дж. Физ. А. 25 (22): 5867–5888. Бибкод : 1992JPhA...25.5867G . дои : 10.1088/0305-4470/25/22/015 .
- ^ Ачарья, М.; Д. Стауффер (1998). «Влияние граничных условий на критическую вероятность охвата». Межд. Дж. Мод. Физ. С. 9 (4): 643–647. arXiv : cond-mat/9805355 . Бибкод : 1998IJMPC...9..643A . дои : 10.1142/S0129183198000534 . S2CID 15684907 .
- ^ Ян, Н.; Д. Стауффер (1998). «Случайное просачивание сайтов в трех измерениях». Межд. Дж. Мод. Физ. С. 9 (4): 341–347. Бибкод : 1998IJMPC...9..341J . дои : 10.1142/S0129183198000261 .
- ^ Дэн, Юджин; HWJ Блёте (2005). «Исследование модели перколяции сайтов в двух и трех измерениях методом Монте-Карло» . Физический обзор E . 72 (1): 016126. Бибкод : 2005PhRvE..72a6126D . дои : 10.1103/PhysRevE.72.016126 . ПМИД 16090055 .
- ^ Баллестерос, Пенсильвания; Л.А. Фернандес; В. Мартин-Майор; А. Муньос Судепе; Г. Паризи; Джей Джей Руис-Лоренцо (1999). «Поправки к масштабированию: просачивание участков и модель Изинга в трех измерениях». Журнал физики А. 32 (1): 1–13. arXiv : cond-mat/9805125 . Бибкод : 1999JPhA...32....1B . дои : 10.1088/0305-4470/32/1/004 . S2CID 2787294 .
- ^ Jump up to: а б с Лоренц, CD; Р. М. Зифф (1998). «Универсальность избыточного числа кластеров и функция вероятности пересечения в трехмерной перколяции». Журнал физики А. 31 (40): 8147–8157. arXiv : cond-mat/9806224 . Бибкод : 1998JPhA...31.8147L . дои : 10.1088/0305-4470/31/40/009 . S2CID 12493873 .
- ^ Jump up to: а б с д и ж г час я дж к Коза, Збигнев; Якуб Пола (2016). «От дискретной к непрерывной перколяции в измерениях от 3 до 7». Журнал статистической механики: теория и эксперимент . 2016 (10): 103206. arXiv : 1606.08050 . Бибкод : 2016JSMTE..10.3206K . дои : 10.1088/1742-5468/2016/10/103206 . S2CID 118580056 .
- ^ Шквор, Иржи; Иво Незбеда (2009). «Пороговые параметры перколяции жидкостей». Физический обзор E . 79 (4): 041141. Бибкод : 2009PhRvE..79d1141S . дои : 10.1103/PhysRevE.79.041141 . ПМИД 19518207 .
- ^ Jump up to: а б с д Адлер, Джоан; Игаль Меир; Амнон Ахароний; АБ Харрис; Лиор Кляйн (1990). «Серия низких концентраций в общем измерении». Журнал статистической физики . 58 (3/4): 511–538. Бибкод : 1990JSP....58..511A . дои : 10.1007/BF01112760 . S2CID 122109020 .
- ^ Jump up to: а б с д и ж г час Даммер, Стефан М; Хэй Хинриксен (2004). «Распространение иммунизации в больших масштабах». Журнал статистической механики: теория и эксперимент . 2004 (7): P07011. arXiv : cond-mat/0405577 . Бибкод : 2004JSMTE..07..011D . дои : 10.1088/1742-5468/2004/07/P07011 . S2CID 118981083 .
- ^ Jump up to: а б с Лоренц, CD; Р. М. Зифф (1998). «Точное определение порогов перколяции связей и поправок к масштабированию конечного размера для решеток sc, fcc и bcc». Физический обзор E . 57 (1): 230–236. arXiv : cond-mat/9710044 . Бибкод : 1998PhRvE..57..230L . дои : 10.1103/PhysRevE.57.230 . S2CID 119074750 .
- ^ Jump up to: а б Шренк, К.Дж.; ДНП Араужо; Х.Дж. Херрманн (2013). «Сложенная треугольная решетка: свойства перколяции». Физический обзор E . 87 (3): 032123.arXiv : 1302.0484 . Бибкод : 2013PhRvE..87c2123S . дои : 10.1103/PhysRevE.87.032123 . S2CID 2917074 .
- ^ Мартинс, П.; Дж. Пласкак (2003). «Перколяция на двумерных и трехмерных решетках». Физический обзор . 67 (4): 046119. arXiv : cond-mat/0304024 . Бибкод : 2003PhRvE..67d6119M . дои : 10.1103/physreve.67.046119 . ПМИД 12786448 . S2CID 31891392 .
- ^ Брэдли, РМ; П. Н. Стренский; Ж.-М. Дебьер (1991). «Поверхности перколяционных кластеров в трех измерениях». Физический обзор B . 44 (1): 76–84. Бибкод : 1991PhRvB..44...76B . дои : 10.1103/PhysRevB.44.76 . ПМИД 9998221 .
- ^ Jump up to: а б с д и ж Куржавский, Л.; К. Маларц (2012). «Простые кубические пороги перколяции случайных узлов для сложных окрестностей». Представитель Матем. Физ . 70 (2): 163–169. arXiv : 1111.3254 . Бибкод : 2012РпМП...70..163К . CiteSeerX 10.1.1.743.1726 . дои : 10.1016/S0034-4877(12)60036-6 . S2CID 119120046 .
- ^ Галлямов, СР; С.А. Мельчуков (2013). «Порог перколяции простой кубической решетки с четвертыми соседями: теория и численный расчет с распараллеливанием» (PDF) . Третья международная конференция «Высокопроизводительные вычисления» HPC-UA 2013 (Украина, Киев, 7–11 октября 2013 г.) . Архивировано из оригинала (PDF) 23 августа 2019 года . Проверено 23 августа 2019 г.
- ^ Сайкс, МФ; Д.С. Гонт; Дж. В. Эссам (1976). «Вероятность перколяции задачи узлов на гранецентрированной кубической решетке». Журнал физики А. 9 (5): Л43–Л46. Бибкод : 1976JPhA....9L..43S . дои : 10.1088/0305-4470/9/5/002 .
- ^ Jump up to: а б с д и ж г час я дж к л м н тот п д р с т в v В х и С аа аб и объявление но из в ах Ху, Йи; Патрик Шарбонно (2021). «Пороги перколяции на многомерных D n и E 8 -родственных решетках». Физический обзор E . 103 (6): 062115. arXiv : 2102.09682 . Бибкод : 2021PhRvE.103f2115H . дои : 10.1103/PhysRevE.103.062115 . ПМИД 34271715 . S2CID 231979212 .
- ^ Jump up to: а б Лоренц, CD; Р. Мэй; Р. М. Зифф (2000). «Сходство порогов перколяции на решетках HCP и FCC» (PDF) . Журнал статистической физики . 98 (3/4): 961–970. дои : 10.1023/А:1018648130343 . hdl : 2027.42/45178 . S2CID 10950378 .
- ^ Тахир-Хели, Джамиль; В.А. Годдард III (2007). «Киральная плакет-поляронная теория купратной сверхпроводимости». Физический обзор B . 76 (1): 014514. arXiv : 0707.3535 . Бибкод : 2007PhRvB..76a4514T . дои : 10.1103/PhysRevB.76.014514 . S2CID 8882419 .
- ^ Jump up to: а б с д и ж г Маларц, Кшиштоф (2015). «Простые кубические пороги перколяции случайных узлов для окрестностей, содержащих четвертых ближайших соседей». Физ. Преподобный Е. 91 (4): 043301. arXiv : 1501.01586 . Бибкод : 2015PhRvE..91d3301M . дои : 10.1103/PhysRevE.91.043301 . ПМИД 25974606 . S2CID 37943657 .
- ^ Сюнь, Чжипен; Дапенг Хао; Роберт М. Зифф (2021). «Просачивание узлов на квадратных и простых кубических решетках с расширенными окрестностями и их континуальный предел». Физ. Преподобный Е. 103 (2): 022126. arXiv : 2010.02895 . Бибкод : 2021PhRvE.103b2126X . дои : 10.1103/PhysRevE.103.022126 . ПМИД 33735955 . S2CID 222141832 .
- ^ Jump up to: а б с д и ж г час я дж Сюнь, Чжипен; Роберт М. Зифф (2020). «Просачивание связей на простых кубических решетках с расширенными окрестностями». Физ. Преподобный Е. 102 (4): 012102.arXiv : 2001.00349 . Бибкод : 2020PhRvE.102a2102X . дои : 10.1103/PhysRevE.102.012102 . ПМИД 32795057 . S2CID 209531616 .
- ^ Jump up to: а б с д Джерольд, Греция; Л. Е. Скривен; Х. Т. Дэвис (1984). «Просачивание и проводимость в трехмерных сетях Вороного и регулярных сетях: второй пример топологического беспорядка». Дж. Физ. C: Физика твердого тела . 17 (19): 3429–3439. Бибкод : 1984JPhC...17.3429J . дои : 10.1088/0022-3719/17/19/017 .
- ^ Сюй, Фанбо; Чжипин Сюй; Борис Иванович Якобсон (2014). «Порог перколяции по месту волокон углеродных нанотрубок - быстрый контроль перколяции с помощью стохастической теории Маркова». Физика А. 407 : 341–349. arXiv : 1401.2130 . Бибкод : 2014PhyA..407..341X . дои : 10.1016/j.physa.2014.04.013 . S2CID 119267606 .
- ^ Jump up to: а б с Гаурон, ТР; Марек Чеплак (1991). «Пороги перколяции сайтов решетки FCC» (PDF) . Acta Physica Polonica А. 80 (3): 461. Бибкод : 1991AcPPA..80..461G . doi : 10.12693/APhysPolA.80.461 .
- ^ Хартер, Т. (2005). «Масштабный анализ конечного размера перколяции в трехмерных коррелированных случайных полях двоичных цепей Маркова». Физический обзор E . 72 (2): 026120. Бибкод : 2005PhRvE..72b6120H . дои : 10.1103/PhysRevE.72.026120 . ПМИД 16196657 . S2CID 2708506 .
- ^ Сайкс, МФ; Джей Джей Рер; Морин Глен (1996). «Заметка о вероятностях перколяции пар близко подобных решеток». Учеб. Кэмб. Фил. Соц . 76 : 389–392. дои : 10.1017/S0305004100049021 . S2CID 96528423 .
- ^ Вебер, Х.; В. Пол (1996). «Проникающая диффузия в замороженных полимерных матрицах: исследование перколяции в свободном объеме с использованием конечного масштаба». Физический обзор E . 54 (4): 3999–4007. Бибкод : 1996PhRvE..54.3999W . дои : 10.1103/PhysRevE.54.3999 . ПМИД 9965547 .
- ^ Jump up to: а б с д и Митра, С.; Д. Саха; А. Сеншарма (2022). «Просачивание в простой кубической решетке с искажением». Физ. Преподобный Е. 106 (3): 034109. arXiv : 2207.12079 . Бибкод : 2022PhRvE.106c4109M . дои : 10.1103/PhysRevE.106.034109 . ПМИД 36266842 .
- ^ Тарасевич, Ю. Ю.; В.А. Черкасова (2007). «Просачивание димеров и застревание на простой кубической решетке». Европейский физический журнал Б. 60 (1): 97–100. arXiv : 0709.3626 . Бибкод : 2007EPJB...60...97T . дои : 10.1140/epjb/e2007-00321-2 . S2CID 5419806 .
- ^ Холкомб, Д. Ф..; Джей Джей Рер-младший (1969). «Перколяция в сильнолегированных полупроводниках*». Физический обзор . 183 (3): 773–776. Бибкод : 1969PhRv..183..773H . дои : 10.1103/PhysRev.183.773 .
- ^ Холкомб, Д.Ф.; Ф. Холкомб; М. Ивасава (1972). «Кластеризация случайно расположенных сфер». Биометрика . 59 : 207–209. дои : 10.1093/biomet/59.1.207 .
- ^ Шанте, Винод К.С.; Скотт Киркпатрик (1971). «Введение в теорию перколяции». Достижения физики . 20 (85): 325–357. Бибкод : 1971AdPhy..20..325S . дои : 10.1080/00018737100101261 .
- ^ Jump up to: а б Ринтул, доктор медицины; С. Торквато (1997). «Точное определение критического порога и показателей степени в трехмерной модели перколяции континуума». Дж. Физ. А: Математика. Ген . 30 (16): Л585. Бибкод : 1997JPhA...30L.585R . CiteSeerX 10.1.1.42.4284 . дои : 10.1088/0305-4470/30/16/005 .
- ^ Консильо, Р.; Р. Бейкер; Г. Пол; Его Превосходительство Стэнли (2003). «Континуальное просачивание конгруэнтных перекрывающихся сфероцилиндров». Физика А. 319 : 49–55. дои : 10.1016/S0378-4371(02)01501-7 .
- ^ Jump up to: а б с д и ж г час Сюй, Вэньсян; Сянлун Су; Ян Цзяо (2016). «Континуальное просачивание конгруэнтных перекрывающихся сфероцилиндров». Физ. Преподобный Е. 93 (3): 032122. Бибкод : 2016PhRvE..94c2122X . дои : 10.1103/PhysRevE.94.032122 . ПМИД 27078307 .
- ^ Jump up to: а б Лоренц, CD; Р. М. Зифф (2000). «Точное определение критического порога перколяции для трехмерной модели швейцарского сыра с использованием алгоритма роста» (PDF) . Дж. Хим. Физ . 114 (8): 3659. Бибкод : 2001JChPh.114.3659L . дои : 10.1063/1.1338506 . hdl : 2027.42/70114 .
- ^ Jump up to: а б с д и ж г час я Линь, Цзяньцзюнь; Чен, Хуэйсу; Сюй, Вэньсян (2018). «Геометрический порог перколяции конгруэнтных кубовидных частиц в перекрывающихся системах частиц». Физический обзор E . 98 (1): 012134. Бибкод : 2018PhRvE..98a2134L . дои : 10.1103/PhysRevE.98.012134 . ПМИД 30110832 . S2CID 52017287 .
- ^ Jump up to: а б с д и ж г час я дж к л м н тот п д р с т в v В х и С аа аб и объявление но из в ах есть Гарбоци, Э.Дж.; К.А. Снайдер; Дж. Ф. Дуглас (1995). «Геометрический порог перколяции перекрывающихся эллипсоидов» . Физ. Преподобный Е. 52 (1): 819–827. Бибкод : 1995PhRvE..52..819G . дои : 10.1103/PhysRevE.52.819 . ПМИД 9963485 .
- ^ Jump up to: а б с д Ли, Минци; Чен, Хуэйсу; Линь, Цзяньцзюнь (январь 2020 г.). «Эффективное измерение порога перколяции для случайных систем конгруэнтных перекрывающихся овоидов». Порошковая технология . 360 : 598–607. дои : 10.1016/j.powtec.2019.10.044 . ISSN 0032-5910 . S2CID 208693526 .
- ^ Ли, Минци; Чен, Хуэйсу; Линь, Цзяньцзюнь (апрель 2020 г.). «Численное исследование порога перколяции и транспортных свойств пористых композитов, содержащих нецентросимметричные суперовоидальные поры». Компьютерные методы в прикладной механике и технике . 361 : 112815. Бибкод : 2020CMAME.361k2815L . дои : 10.1016/j.cma.2019.112815 . ISSN 0045-7825 . S2CID 213152892 .
- ^ Jump up to: а б с д и ж Далл, Джеспер; Майкл Кристенсен (2002). «Случайные геометрические графы». Физ. Преподобный Е. 66 (1): 016121. arXiv : cond-mat/0203026 . Бибкод : 2002PhRvE..66a6121D . дои : 10.1103/PhysRevE.66.016121 . ПМИД 12241440 . S2CID 15193516 .
- ^ Гори, Джакомо; Андреа Тромбеттони (2015). «Конформная инвариантность в трехмерной перколяции». Журнал статистической механики: теория и эксперимент . 2015 (7): P07014. arXiv : 1504.07209 . Бибкод : 2015JSMTE..07..014G . дои : 10.1088/1742-5468/2015/07/P07014 . S2CID 119292052 .
- ^ Бальберг, И.; Н. Биненбаум (1984). «Пороги перколяции в системе трехмерных палочек». Физ. Преподобный Летт . 52 (17): 1465. Бибкод : 1984PhRvL..52.1465B . дои : 10.1103/PhysRevLett.52.1465 .
- ^ Jump up to: а б с д и ж г час я дж Йи, Ю.-Б.; А. М. Састри (2004). «Аналитическая аппроксимация порога перколяции для перекрывающихся эллипсоидов вращения». Учеб. Р. Сок. Лонд. А. 460 (2048): 2353–2380. Бибкод : 2004RSPSA.460.2353Y . дои : 10.1098/rspa.2004.1279 . S2CID 2475482 .
- ^ Jump up to: а б с Хийтия, Э.; Дж. Виртамо; П. Лассила; Дж. Отт (2012). «Порог непрерывной перколяции для проницаемых выровненных цилиндров и оппортунистических сетей» . Коммуникационные письма IEEE . 16 (7): 1064–1067. дои : 10.1109/LCOMM.2012.051512.120497 . S2CID 1056865 .
- ^ Jump up to: а б с д и Торквато, С.; Ю. Цзяо (2012). «Влияние размерности на порог перколяции перекрывающихся несферических гиперчастиц». Физический обзор E . 87 (2): 022111. arXiv : 1210.0134 . Бибкод : 2013PhRvE..87b2111T . дои : 10.1103/PhysRevE.87.022111 . ПМИД 23496464 . S2CID 11417012 .
- ^ Jump up to: а б с Йи, ЮБ; Э. Таверги (2009). «Геометрические пороги перколяции взаимопроникающих пластин в трехмерном пространстве». Физический обзор E . 79 (4): 041134. Бибкод : 2009PhRvE..79d1134Y . дои : 10.1103/PhysRevE.79.041134 . ПМИД 19518200 .
- ^ Jump up to: а б с Пауэлл, MJ (1979). «Просачивание сайта в случайно упакованные сферы». Физический обзор B . 20 (10): 4194–4198. Бибкод : 1979PhRvB..20.4194P . дои : 10.1103/PhysRevB.20.4194 .
- ^ Jump up to: а б Зифф, РМ; Сальваторе Торквато (2016). «Просачивание неупорядоченных упаковок заклиненных сфер». Физический журнал A: Математический и теоретический . 50 (8): 085001. arXiv : 1611.00279 . Бибкод : 2017JPhA...50h5001Z . дои : 10.1088/1751-8121/aa5664 . S2CID 53003822 .
- ^ Jump up to: а б с д и ж Йи, ЮБ; К. Эсмаил (2012). «Вычислительное измерение порогов перколяции пустот сплюснутых частиц и тонких пластинчатых композитов». Дж. Прил. Физ . 111 (12): 124903–124903–6. Бибкод : 2012JAP...111l4903Y . дои : 10.1063/1.4730333 .
- ^ Линь, Цзяньцзюнь; Чен, Хуэйсу (2018). «Непрерывное просачивание пористых сред посредством случайной упаковки перекрывающихся кубообразных частиц» . Письма по теоретической и прикладной механике . 8 (5): 299–303. дои : 10.1016/j.taml.2018.05.007 .
- ^ Линь, Цзяньцзюнь; Чен, Хуэйсу (2018). «Влияние морфологии частиц на просачивание частиц пористой среды: исследование супершаров». Порошковая технология . 335 : 388–400. дои : 10.1016/j.powtec.2018.05.015 . S2CID 103471554 .
- ^ Jump up to: а б с д и ж г час я дж к л Прайор-младший, диджей; Нью-Джерси Макгиган (2018). «Просачивание через пустоты вокруг случайно ориентированных многогранников и осесимметричных зерен». Физ. Преподобный Летт . 121 (22): 225701. arXiv : 1801.09970 . Бибкод : 2018PhRvL.121v5701P . doi : 10.1103/PhysRevLett.121.225701 . ПМИД 30547614 . S2CID 119185480 .
- ^ Jump up to: а б с д и ж г час я Новак Игорь Л.; Фэй Гао; Павел Крайковский; Борис Михайлович Слепченко (2011). «Диффузия среди случайных перекрывающихся препятствий: сходства, инварианты, аппроксимации» . Дж. Хим. Физ . 134 (15): 154104. Бибкод : 2011JChPh.134o4104N . дои : 10.1063/1.3578684 . ПМК 3094463 . ПМИД 21513372 .
- ^ Jump up to: а б с д и ж Йи, Ю.Б. (2006). «Просачивание пустот и проводимость перекрывающихся эллипсоидов». Физический обзор E . 74 (3): 031112. Бибкод : 2006PhRvE..74c1112Y . дои : 10.1103/PhysRevE.74.031112 . ПМИД 17025599 .
- ^ Jump up to: а б с д и ж г час я дж к л м н Баллоу, А.; П. Линтон; Диджей Прайор младший (2023). «Просачивание через пустоты вокруг тороидальных включений». Физический обзор E . 107 (1): 014902. arXiv : 2208.10582 . Бибкод : 2023PhRvE.107a4902B . дои : 10.1103/PhysRevE.107.014902 . ПМИД 36797924 . S2CID 251741342 .
- ^ Jump up to: а б Прайор-младший, диджей; Нью-Джерси Макгиган (2017). «Просачивание через пустоты вокруг случайно ориентированных граненых включений». arXiv : 1712.10241 [ cond-mat.stat-mech ].
- ^ Кертес, Янош (1981). «Просачивание дыр между перекрывающимися сферами: расчет критической объемной доли методом Монте-Карло» (PDF) . Журнал Physique Lettres . 42 (17): Л393–Л395. doi : 10.1051/jphyslet:019810042017039300 . S2CID 122115573 .
- ^ Элам, Западная Каролина; А.Р. Керштейн; Джей Джей Рер (1984). «Критические свойства проблемы просачивания пустот для сфер». Физ. Преподобный Летт . 52 (7): 1516–1519. Бибкод : 1984PhRvL..52.1516E . дои : 10.1103/PhysRevLett.52.1516 .
- ^ Ринтул, доктор медицины (2000). «Точное определение порога просачивания пустот для двух распределений перекрывающихся сфер» . Физический обзор E . 62 (6): 68–72. Бибкод : 2000PhRvE..62...68R . дои : 10.1103/PhysRevE.62.68 . ПМИД 11088435 .
- ^ Jump up to: а б Хёфлинг, Ф.; Т. Мунк; Э. Фрей; Т. Франош (2008). «Критическая динамика баллистических и броуновских частиц в гетерогенной среде». Дж. Хим. Физ . 128 (16): 164517. arXiv : 0712.2313 . Бибкод : 2008JChPh.128p4517H . дои : 10.1063/1.2901170 . ПМИД 18447469 . S2CID 25509814 .
- ^ Прайор-младший, диджей (2014). «Просачивание через пустоты вокруг перекрывающихся сфер: динамический анализ масштабирования конечного размера». Физ. Преподобный Е. 89 (1): 012148. arXiv : 1208.0328 . Бибкод : 2014PhRvE..89a2148P . дои : 10.1103/PhysRevE.89.012148 . ПМИД 24580213 . S2CID 20349307 .
- ^ Клерк, JP; Г. Жиро; С. Александр; Э. Гийон (1979). «Проводимость смеси проводящих и изолирующих зерен: эффекты размерности». Физический обзор B . 22 (5): 2489–2494. дои : 10.1103/PhysRevB.22.2489 .
- ^ К. Лармье; Э. Дюмонтей; Ф. Мальваги; А. Маццоло; А. Зоя (2016). «Эффекты конечного размера и перколяционные свойства геометрий Пуассона». Физический обзор E . 94 (1): 012130. arXiv : 1605.04550 . Бибкод : 2016PhRvE..94a2130L . дои : 10.1103/PhysRevE.94.012130 . ПМИД 27575099 . S2CID 19361619 .
- ^ Jump up to: а б с д и ж Закалюкин Р.М.; В.А. Чижиков (2005). «Расчеты порогов перколяции трехмерной (икосаэдрической) плитки Пенроуза методом кубической аппроксимации». Кристаллографические отчеты . 50 (6): 938–948. Бибкод : 2005CryRp..50..938Z . дои : 10.1134/1.2132400 . S2CID 94290876 .
- ^ Кантор, Яков (1986). «Трехмерная перколяция с удаленными линиями участков». Физ. Преподобный Б. 33 (5): 3522–3525. Бибкод : 1986PhRvB..33.3522K . дои : 10.1103/PhysRevB.33.3522 . ПМИД 9938740 .
- ^ Шренк, К.Дж.; г-н Иларио; В. Сидоравичюс; ДНП Араужо; Х.Дж. Херрманн; М. Тильманн; А. Тейшейра (2016). «Критические свойства фрагментации при случайном сверлении: сколько отверстий нужно просверлить, чтобы разрушить деревянный куб?». Физ. Преподобный Летт . 116 (5): 055701. arXiv : 1601.03534 . Бибкод : 2016PhRvL.116e5701S . doi : 10.1103/PhysRevLett.116.055701 . ПМИД 26894717 . S2CID 3145131 .
- ^ Грассбергер, П. (2017). «Некоторые замечания по поводу бурения перколяции» . Физ. Преподобный Е. 95 (1): 010103. arXiv : 1611.07939 . дои : 10.1103/PhysRevE.95.010103 . ПМИД 28208497 . S2CID 12476714 .
- ^ Грассбергер, Питер; Марсело Р. Иларио; Владас Сидоравичюс (2017). «Просачивание в СМИ с столбчатым расстройством». J.Stat. Физ . 168 (4): 731–745. arXiv : 1704.04742 . Бибкод : 2017JSP...168..731G . дои : 10.1007/s10955-017-1826-7 . S2CID 15915864 .
- ^ Jump up to: а б Щигел, Бартломей; Камил Квятковски; Мацей Левенштейн; Джеральд Джон Лапейр-младший; Ян Вер (2016). «Пороги перколяции для дискретно-непрерывных моделей с неоднородными вероятностями образования связей». Физ. Преподобный Е. 93 (2): 022127. arXiv : 1509.07401 . Бибкод : 2016PhRvE..93b2127S . дои : 10.1103/PhysRevE.93.022127 . ПМИД 26986308 . S2CID 18110437 .
- ^ Абете, Т.; А. де Кандиа; Д. Лайрес; А. Конильо (2004). «Модель перколяции для деградации ферментного геля». Физ. Преподобный Летт . 93 : 228301. arXiv : cond-mat/0402551 . doi : 10.1103/PhysRevLett.93.228301 .
- ^ Jump up to: а б с Киркпатрик, Скотт (1976). «Явление перколяции в более высоких измерениях: подход к пределу среднего поля». Письма о физических отзывах . 36 (2): 69–72. Бибкод : 1976PhRvL..36...69K . дои : 10.1103/PhysRevLett.36.69 .
- ^ Jump up to: а б с д Гонт, Д.С.; Сайкс, МФ; Раскин, Хизер (1976). «Процессы перколяции в d-мерностях». Дж. Физ. А: Математика. Ген . 9 (11): 1899–1911. Бибкод : 1976JPhA....9.1899G . дои : 10.1088/0305-4470/11.09.015 .
- ^ Jump up to: а б с д и ж г час я дж к л м н тот п д р с т Грассбергер, Питер (2003). «Критическое просачивание в большие измерения». Физический обзор E . 67 (3): 4. arXiv : cond-mat/0202144 . Бибкод : 2003PhRvE..67c6101G . дои : 10.1103/PhysRevE.67.036101 . ПМИД 12689126 . S2CID 43707822 .
- ^ Jump up to: а б Пол, Джеральд; Роберт М. Зифф; Х. Юджин Стэнли (2001). «Порог перколяции, показатель Фишера и показатель кратчайшего пути для четырех и пяти измерений». Физический обзор E . 64 (2): 8. arXiv : cond-mat/0101136 . Бибкод : 2001PhRvE..64b6115P . дои : 10.1103/PhysRevE.64.026115 . ПМИД 11497659 . S2CID 18271196 .
- ^ Бальестерос, Х.Г.; Л.А. Фернандес; В. Мартин-Майор; А. Муньос Судупе; Г. Паризи; Джей Джей Руис-Лоренцо (1997). «Меры критических показателей в четырехмерном просачивании сайтов». Физ. Письмо Б. 400 (3–4): 346–351. arXiv : hep-lat/9612024 . Бибкод : 1997PhLB..400..346B . дои : 10.1016/S0370-2693(97)00337-7 . S2CID 10242417 .
- ^ Jump up to: а б с д и ж г Котвица, М.; П. Гронек; К. Маларц (2019). «Эффективная виртуализация пространства для алгоритма Хошена – Копельмана». Международный журнал современной физики C . 30 (8): 1950055–1950099. arXiv : 1803.09504 . Бибкод : 2019IJMPC..3050055K . дои : 10.1142/S0129183119500554 . S2CID 4418563 .
- ^ Jump up to: а б с д и ж г час я дж к л м н тот п д р с т Мертенс, Стефан; Кристофер Мур (2018). «Пороги перколяции и показатели Фишера в гиперкубических решетках». Физ. Преподобный Е. 98 (2): 022120.arXiv : 1806.08067 . Бибкод : 2018PhRvE..98b2120M . дои : 10.1103/PhysRevE.98.022120 . ПМИД 30253462 . S2CID 52821851 .
- ^ Jump up to: а б с д Харрис, AB; Фиш, Р. (1977). «Критическое поведение случайных резисторных сетей» . Письма о физических отзывах . 38 (15): 796–799. Бибкод : 1977PhRvL..38..796H . doi : 10.1103/PhysRevLett.38.796 .
- ^ Jump up to: а б с д Сюнь, Чжипен (2020). «Точные пороги перколяции связей на нескольких четырехмерных решетках». Обзор физических исследований . 2 (1): 013067. arXiv : 1910.11408 . Бибкод : 2020PhRvR...2a3067X . doi : 10.1103/PhysRevResearch.2.013067 . S2CID 204915841 .
- ^ Jump up to: а б Гонт, Д.С.; Раскин, Хизер (1978). «Процессы перколяции связей в d-размерах». Дж. Физ. А: Математика. Ген . 11 (7): 1369. Бибкод : 1978JPhA...11.1369G . дои : 10.1088/0305-4470/7.11.025 .
- ^ Jump up to: а б с д и Адлер, Джоан; Игаль Меир; Амнон Ахароний; АБ Харрис (1990). «Серийное исследование моментов перколяции в общем измерении» . Физический обзор B . 41 (13): 9183–9206. Бибкод : 1990PhRvB..41.9183A . дои : 10.1103/PhysRevB.41.9183 . ПМИД 9993262 .
- ^ Штауффер, Дитрих; Роберт М. Зифф (1999). «Повторное исследование семимерных порогов просачивания сайтов». Международный журнал современной физики C . 11 (1): 205–209. arXiv : cond-mat/9911090 . Бибкод : 2000IJMPC..11..205S . дои : 10.1142/S0129183100000183 . S2CID 119362011 .
- ^ Мертенс, Стефан; Мур, Кристофер (2018). «Разложение в ряд критических плотностей перколяции на ℤ д ". J. Phys. A: Math. Theor . 51 (47): 475001. arXiv : 1805.02701 . doi : 10.1088/1751-8121/aae65c . S2CID 119399128 .
- ^ Jump up to: а б с д и ж г час я дж к л м н тот п д р Чжао, Пэнъюй; Цзиньхун Ян; Чжипен Сюнь; Дапенг Хао; Роберт М. Зифф (2022). «Просачивание узлов и связей на четырехмерных простых гиперкубических решетках с расширенными окрестностями». Журнал статистической механики: теория и эксперимент . 2022 (3): 033202. arXiv : 2109.11195 . Бибкод : 2022JSMTE2022c3202Z . дои : 10.1088/1742-5468/ac52a8 . S2CID 237605083 .
- ^ Jump up to: а б Лёбл, Матиас К. (2024). «Архитектура, устойчивая к потерям, для квантовых вычислений с квантовыми эмиттерами». Квантовый . 8 : 1302. arXiv : 2304.03796 . doi : 10.22331/q-2024-03-28-1302 .
- ^ Jump up to: а б Шульман, Л.С. (1983). «Просачивание на большие расстояния в одном измерении». Журнал физики A: Математический и общий . 16 (17): Л639–Л641. Бибкод : 1983JPhA...16L.639S . дои : 10.1088/0305-4470/16/17/001 . ISSN 0305-4470 .
- ^ Айзенман, М.; Ньюман, CM (1 декабря 1986 г.). «Разрыв плотности перколяции в одномерных моделях перколяции 1/|x-y|2». Связь в математической физике . 107 (4): 611–647. Бибкод : 1986CMaPh.107..611A . дои : 10.1007/BF01205489 . ISSN 0010-3616 . S2CID 117904292 .
- ^ Jump up to: а б Гори, Г.; Микеланджели, М.; Дефеню, Н.; Тромбеттони, А. (2017). «Одномерная перколяция на большие расстояния: численное исследование». Физический обзор E . 96 (1): 012108.arXiv : 1610.00200 . Бибкод : 2017PhRvE..96a2108G . дои : 10.1103/physreve.96.012108 . ПМИД 29347133 . S2CID 9926800 .
- ^ Бэк, СК; Петтер Миннхаген; Бом Джун Ким (2009). «Комментарий к «Исследованию двухэтапного перколяционного перехода в улучшенных двоичных деревьях методом моделирования Монте-Карло» ». Дж. Физ. А: Математика. Теор . 42 (47): 478001. arXiv : 0910.4340 . Бибкод : 2009JPhA...42U8001B . дои : 10.1088/1751-8113/42/47/478001 . S2CID 102489139 .
- ^ Jump up to: а б с Бетчер, Стефан; Джессика Л. Кук; Роберт М. Зифф (2009). «Неоднородное проникновение в иерархическую сеть со связями маленького мира». Физ. Преподобный Е. 80 (4): 041115. arXiv : 0907.2717 . Бибкод : 2009PhRvE..80d1115B . дои : 10.1103/PhysRevE.80.041115 . ПМИД 19905281 . S2CID 119265110 .
- ^ Jump up to: а б с д и ж г час я дж к л м н тот п д р с т в v В х и С аа аб и объявление но из в ах есть также и аль являюсь а Мертенс, Стефан; Кристофер Мур (2017). «Пороги перколяции в гиперболических решетках». Физ. Преподобный Е. 96 (4): 042116. arXiv : 1708.05876 . Бибкод : 2017PhRvE..96d2116M . дои : 10.1103/PhysRevE.96.042116 . ПМИД 29347529 . S2CID 39025690 .
- ^ Jump up to: а б с Лопес, Хорхе Х.; Дж. М. Шварц (2017). «Просачивание ограничений на гиперболических решетках». Физ. Преподобный Е. 96 (5): 052108. arXiv : 1512.05404 . Бибкод : 2017PhRvE..96e2108L . дои : 10.1103/PhysRevE.96.052108 . ПМИД 29347694 . S2CID 44770310 .
- ^ Jump up to: а б с д и ж г час я Бэк, СК; Петтер Миннхаген; Бом Джун Ким (2009). «Перколяция на гиперболических решетках». Физ. Преподобный Е. 79 (1): 011124. arXiv : 0901.0483 . Бибкод : 2009PhRvE..79a1124B . дои : 10.1103/PhysRevE.79.011124 . ПМИД 19257018 . S2CID 29468086 .
- ^ Jump up to: а б с д и ж г час Гу, Ханг; Роберт М. Зифф (2012). «Пересечение на гиперболических решетках». Физ. Преподобный Е. 85 (5): 051141. arXiv : 1111.5626 . Бибкод : 2012PhRvE..85e1141G . дои : 10.1103/PhysRevE.85.051141 . ПМИД 23004737 . S2CID 7141649 .
- ^ Jump up to: а б с д Ногава, Томоаки; Такехиса Хасегава (2009). «Исследование методом моделирования методом Монте-Карло двухэтапного перколяционного перехода в улучшенных двоичных деревьях». Дж. Физ. А: Математика. Теор . 42 (14): 145001. arXiv : 0810.1602 . Бибкод : 2009JPhA...42n5001N . дои : 10.1088/1751-8113/42/14/145001 . S2CID 118367190 .
- ^ Jump up to: а б Миннхаген, Петтер; Сын Ки Бэк (2010). «Аналитические результаты перколяционных переходов расширенного двоичного дерева». Физ. Преподобный Е. 82 (1): 011113. arXiv : 1003.6012 . Бибкод : 2010PhRvE..82a1113M . дои : 10.1103/PhysRevE.82.011113 . ПМИД 20866571 . S2CID 21018113 .
- ^ Козакова, Ива (2009). «Критическое проникновение виртуально свободных групп и других древовидных графов». Анналы вероятности . 37 (6): 2262–2296. arXiv : 0801.4153 . дои : 10.1214/09-AOP458 .
- ^ Jump up to: а б с д и ж г час я дж к л м н тот п д р с т в v В х и С аа аб и объявление но из в ах Ван, Цзюньфэн; Цзунчжэн Чжоу; Цинцюань Лю; Тимоти М. Гарони; Юджин Дэн (2013). «Высокоточное исследование направленной перколяции методом Монте-Карло в измерениях (d + 1)». Физический обзор E . 88 (4): 042102. arXiv : 1201.3006 . Бибкод : 2013PhRvE..88d2102W . дои : 10.1103/PhysRevE.88.042102 . ПМИД 24229111 . S2CID 43011467 .
- ^ Jump up to: а б Дженсен, Иван ; Энтони Дж. Гуттманн (1995). «Разложение в ряд вероятности перколяции для направленных квадратных и сотовых решеток». Дж. Физ. А: Математика. Ген . 28 (17): 4813–4833. arXiv : cond-mat/9509121 . Бибкод : 1995JPhA...28.4813J . дои : 10.1088/0305-4470/28/17/015 . S2CID 118993303 .
- ^ Jump up to: а б Дженсен, Иван (2004). «Разложения в ряд низкой плотности для направленной перколяции: III. Некоторые двумерные решетки». Дж. Физ. А: Математика. Ген . 37 (4): 6899–6915. arXiv : cond-mat/0405504 . Бибкод : 2004JPhA...37.6899J . CiteSeerX 10.1.1.700.2691 . дои : 10.1088/0305-4470/37/27/003 . S2CID 119326380 .
- ^ Jump up to: а б с д Эссам, Дж.В.; Эй Джей Гутманн; К. Де'Белл (1988). «О двумерной направленной перколяции». Дж. Физ. А. 21 (19): 3815–3832. Бибкод : 1988JPhA...21.3815E . дои : 10.1088/0305-4470/21/19/018 .
- ^ Любек, С.; РД Уиллманн (2002). «Универсальное масштабирование направленной перколяции и парного контактного процесса во внешнем поле». Дж. Физ. А. 35 (48): 10205. arXiv : cond-mat/0210403 . Бибкод : 2002JPhA...3510205L . дои : 10.1088/0305-4470/35/48/301 . S2CID 11831269 .
- ^ Jump up to: а б Дженсен, Иван (1999). «Разложение в ряд низкой плотности для направленной перколяции: I. Новый эффективный алгоритм с приложениями к квадратной решетке». Дж. Физ. А. 32 (28): 5233–5249. arXiv : cond-mat/9906036 . Бибкод : 1999JPhA...32.5233J . дои : 10.1088/0305-4470/32/28/304 . S2CID 2681356 .
- ^ Эссам, Джон; К. Де'Белл; Дж. Адлер ; Ф.М. Бхатти (1986). «Анализ расширенных рядов для перколяции связей на направленной квадратной решетке». Физический обзор B . 33 (2): 1982–1986. Бибкод : 1986PhRvB..33.1982E . doi : 10.1103/PhysRevB.33.1982 . ПМИД 9938508 .
- ^ Бакстер, Р.Дж.; Эй Джей Гутманн (1988). «Разложение в ряд вероятности перколяции для направленной квадратной решетки». Дж. Физ. А. 21 (15): 3193–3204. Бибкод : 1988JPhA...21.3193B . дои : 10.1088/0305-4470/21/15/008 .
- ^ Jump up to: а б с Дженсен, Иван (1996). «Разложения в ряды низкой плотности для направленной перколяции на квадратных и треугольных решетках». Дж. Физ. А. 29 (22): 7013–7040. Бибкод : 1996JPhA...29.7013J . дои : 10.1088/0305-4470/29/22/007 . S2CID 121332666 .
- ^ Jump up to: а б с д и ж г час я дж Близ, Дж. (1977). «Разложение в ряд для задачи перколяции направленных связей». Дж. Физ. C: Физика твердого тела . 10 (7): 917–924. Бибкод : 1977JPhC...10..917B . дои : 10.1088/0022-3719/10/7/003 .
- ^ Jump up to: а б с Грассбергер, П.; Ю.-К. Чжан (1996). « Самоорганизованная» формулировка стандартных явлений перколяции». Физика А. 224 (1): 169–179. Бибкод : 1996PhyA..224..169G . дои : 10.1016/0378-4371(95)00321-5 .
- ^ Jump up to: а б с д и ж Грассбергер, П. (2009). «Локальная устойчивость при направленной перколяции». Журнал статистической механики: теория и эксперимент . 2009 (8): P08021. arXiv : 0907.4021 . Бибкод : 2009JSMTE..08..021G . дои : 10.1088/1742-5468/2009/08/P08021 . S2CID 119236556 .
- ^ Jump up to: а б с д Любек, С.; РД Уиллманн (2004). «Универсальное масштабирование направленной перколяции вокруг верхнего критического измерения». Дж. Стат. Физ . 115 (5–6): 1231–1250. arXiv : cond-mat/0401395 . Бибкод : 2004JSP...115.1231L . CiteSeerX 10.1.1.310.8700 . дои : 10.1023/B:JOSS.0000028059.24904.3b . S2CID 16267627 .
- ^ Перлсман, Э.; С. Хэвлин (2002). «Метод оценки критических показателей с использованием численных исследований» . Еврофиз. Летт . 58 (2): 176–181. Бибкод : 2002EL.....58..176P . дои : 10.1209/epl/i2002-00621-7 . S2CID 67818664 .
- ^ Адлер, Джоан ; Дж. Бергер; МАМС Дуарте; Ю. Меир (1988). «Направленная перколяция в измерениях 3+1». Физический обзор B . 37 (13): 7529–7533. Бибкод : 1988PhRvB..37.7529A . дои : 10.1103/PhysRevB.37.7529 . ПМИД 9944046 .
- ^ Jump up to: а б Грассбергер, Питер (2009). «Логарифмические поправки в (4 + 1)-мерной направленной перколяции». Физический обзор E . 79 (5): 052104. arXiv : 0904.0804 . Бибкод : 2009PhRvE..79e2104G . дои : 10.1103/PhysRevE.79.052104 . ПМИД 19518501 . S2CID 23876626 .
- ^ Соареш, Дэниел Дж.Б.; Хосе С. Андраде-младший; Ханс Дж. Херрманн (2006). «Точный расчет порога различных моделей направленной перколяции на квадратной решетке». Дж. Физ. А: Математика. Ген . 38 (21): Л413–Л415. arXiv : cond-mat/0503408 . дои : 10.1088/0305-4470/38/21/L06 .
- ^ Третьяков А. Ю.; Н Инуи (1995). «Критическое поведение для смешанной перколяции, направленной на связь между сайтами». Дж. Физ. А: Математика. Ген . 28 (14): 3985–3990. arXiv : cond-mat/9505019 . Бибкод : 1995JPhA...28.3985T . дои : 10.1088/0305-4470/28/14/017 .
- ^ Ву, финансовый год (2010). «Критическая граница моделей Поттса и перколяции на решетках треугольного типа и типа кагоме I: выражения в замкнутой форме». Физический обзор E . 81 (6): 061110. arXiv : 0911.2514 . Бибкод : 2010PhRvE..81f1110W . дои : 10.1103/PhysRevE.81.061110 . ПМИД 20866381 . S2CID 31590247 .
- ^ Дамаванди, Оджан Хатиб; Роберт М. Зифф (2015). «Просачивание по гиперграфам с четырьмя ребрами». Дж. Физ. А: Математика. Теор . 48 (40): 405004. arXiv : 1506.06125 . Бибкод : 2015JPhA...48N5004K . дои : 10.1088/1751-8113/48/40/405004 . S2CID 118481075 .
- ^ Jump up to: а б Ву, финансовый год (2006). «Новые критические границы для моделей Поттса и перколяции». Письма о физических отзывах . 96 (9): 090602. arXiv : cond-mat/0601150 . Бибкод : 2006PhRvL..96i0602W . CiteSeerX 10.1.1.241.6346 . doi : 10.1103/PhysRevLett.96.090602 . ПМИД 16606250 . S2CID 15182833 .






































![{\display style p_{b}p_{s}[1-({\sqrt {p_{bc}}}/(3-p_{bc}))({\sqrt {p_{b}}}-{\ sqrt {p_{bc}}}]=p_{bc}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/841ca3acd9efa5a314d4308e4cae70eacb5fd1e5)

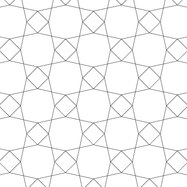

















































![{\displaystyle \eta _ {c} = (\pi ^{d/2}/\Gamma [d/2+1])r^{d}N/L^{d}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90173c0ef117e66cd6feaf99b7e0f615aa0d83b7)
































![{\displaystyle 1-3z+z^{3}-(1-z^{2})[3x^{2}y(1+yy^{2})(1+z)+x^{3}y ^{2}(3-2y)(1+2z)]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bca37fb3504d909546e2e4e7311696782d08b37c)




