Фазовая диаграмма

Фазовая диаграмма в физической химии , технике , минералогии и материаловедении — это тип диаграммы, используемый для отображения условий (давление, температура и т. д.), при которых термодинамически различные фазы (например, твердые, жидкие или газообразные состояния) возникают и сосуществуют при равновесие .

Обзор

Общими компонентами фазовой диаграммы являются линии равновесия или фазовые границы , которые относятся к линиям, обозначающим условия, при которых несколько фаз могут сосуществовать в равновесии. Фазовые переходы происходят вдоль линий равновесия. Метастабильные фазы не показаны на фазовых диаграммах, поскольку, несмотря на их распространенность, они не являются равновесными фазами.

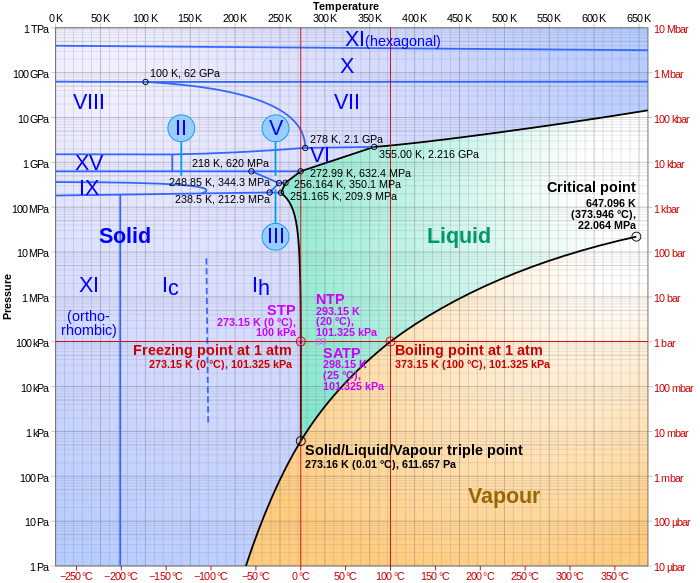
Тройные точки — это точки на фазовых диаграммах, где пересекаются линии равновесия. Тройные точки обозначают условия, при которых могут сосуществовать три разные фазы. Например, на фазовой диаграмме воды есть тройная точка, соответствующая единым температуре и давлению, при которых твердая, жидкая и газообразная вода могут сосуществовать в устойчивом равновесии ( 273,16 К и парциальное давление пара 611,657 Па ). Давление на диаграмме давление-температура (например, показанной на диаграмме состояния воды) представляет собой парциальное давление рассматриваемого вещества. ^[1]

Солидус – это температура , ниже которой вещество стабильно в твердом состоянии. Ликвидус – это температура, выше которой вещество устойчиво в жидком состоянии. Между солидусом и ликвидусом может существовать разрыв; внутри зазора вещество состоит из смеси кристаллов и жидкости (наподобие « суспензии »). ^[2]

Рабочие жидкости часто классифицируют на основе формы их фазовой диаграммы.

Типы

2-мерные диаграммы

Давление против температуры

Типичная фазовая диаграмма. Сплошная зеленая линия показывает поведение температуры плавления большинства веществ; пунктирная зеленая линия показывает аномальное поведение воды . Красные линии показывают температуру сублимации , а синяя линия — температуру кипения , показывая, как они изменяются в зависимости от давления.

Простейшие фазовые диаграммы представляют собой диаграммы давления и температуры одного простого вещества, например воды . Оси соответствуют давлению и температуре . Фазовая диаграмма показывает в пространстве давление-температура линии равновесия или фазовые границы между тремя фазами: твердой , жидкой и газообразной .

Кривые на фазовой диаграмме показывают точки, в которых свободная энергия (и другие производные свойства) становятся неаналитическими: их производные по координатам (в данном случае температуре и давлению) изменяются скачком (скачком). Например, теплоемкость контейнера, наполненного льдом, резко изменится, когда контейнер нагреется выше точки плавления. Открытые пространства, где свободная энергия аналитична , соответствуют однофазным областям. Однофазные области разделены линиями неаналитического поведения, где происходят фазовые переходы , которые называются фазовыми границами .

На диаграмме справа граница фаз между жидкостью и газом не продолжается бесконечно. Вместо этого он заканчивается в точке фазовой диаграммы, называемой критической точкой . Это отражает тот факт, что при чрезвычайно высоких температурах и давлениях жидкая и газообразная фазы становятся неразличимыми. ^[3] в так называемой сверхкритической жидкости . В воде критическая точка возникает при температуре около T _c = 647,096 К (373,946 ° C), p _c = 22,064 МПа (217,75 атм) и ρ _c = 356 кг/м. ³. ^[4]

Существование критической точки жидкость–газ обусловливает некоторую неоднозначность в обозначении однофазных областей. При переходе из жидкой фазы в газообразную фазу обычно пересекают границу фаз, но можно выбрать путь, который никогда не пересекает границу, идя вправо от критической точки. Таким образом, жидкая и газообразная фазы могут непрерывно смешиваться друг с другом. Граница твердой и жидкой фаз может заканчиваться в критической точке только в том случае, если твердая и жидкая фазы имеют одну и ту же группу симметрии . ^[5]

Для большинства веществ граница твердой и жидкой фаз (или кривая плавления) на фазовой диаграмме имеет положительный наклон , поэтому температура плавления увеличивается с ростом давления. Это верно, когда твердая фаза плотнее жидкой. ^[6] Чем больше давление на данное вещество, тем ближе молекулы вещества приближаются друг к другу, что усиливает действие межмолекулярных сил вещества . Таким образом, веществу требуется более высокая температура, чтобы его молекулы имели достаточно энергии, чтобы вырваться из фиксированного рисунка твердой фазы и перейти в жидкую фазу. Аналогичная концепция применима и к фазовым переходам жидкость-газ. ^[7]

Исключением является вода, которая имеет границу твердого тела и жидкости с отрицательным наклоном, так что температура плавления снижается с ростом давления. Это происходит потому, что лед (твердая вода) менее плотный, чем жидкая вода, о чем свидетельствует тот факт, что лед плавает на воде. На молекулярном уровне лед менее плотный, поскольку имеет более обширную сеть водородных связей , что требует большего разделения молекул воды. ^[6] Другие исключения включают сурьму и висмут . ^[8]^[9]

При очень высоких давлениях выше 50 ГПа (500 000 атм) жидкий азот претерпевает фазовый переход жидкость-жидкость в полимерную форму и становится более плотным, чем твердый азот при том же давлении. Следовательно, в этих условиях твердый азот также плавает в жидкости. ^[10]

Величина наклона d P /d T определяется уравнением Клаузиуса–Клапейрона для плавления (плавления) ^[11]

{\frac {\mathrm {d} P}{\mathrm {d} T}}={\frac {\Delta H_{\text{fus}}}{T\,\Delta V_{\text{fus}}}},

где Δ H _fus — теплота плавления, которая всегда положительна, а Δ V _fus — изменение объема при плавлении. Для большинства веществ Δ V _fus положителен, поэтому наклон положителен. Однако для воды и других исключений Δ V _fus отрицательна, поэтому наклон будет отрицательным.

Другие термодинамические свойства

Помимо температуры и давления, на фазовых диаграммах можно отобразить и другие термодинамические свойства. Примеры таких термодинамических свойств включают удельный объем , удельную энтальпию или удельную энтропию . Например, однокомпонентные графики зависимости температуры от удельной энтропии ( T от s ) для воды/ пара или хладагента обычно используются для иллюстрации термодинамических циклов, таких как цикл Карно , цикл Ренкина или цикл охлаждения с паровым сжатием .

Любые две термодинамические величины можно отобразить на горизонтальной и вертикальной осях двумерной диаграммы. Каждая дополнительная термодинамическая величина может быть проиллюстрирована с шагом в виде серии линий — изогнутых, прямых или комбинации изогнутых и прямых. Каждая из этих изолиний представляет собой термодинамическую величину при определенном постоянном значении.

Диаграмма в единицах США
Диаграмма энтальпия-энтропия ( h – s ) для пара
Диаграмма давление-энтальпия ( p – h ) для пара
Диаграмма температура-энтропия ( T – s ) для пара

3-мерные диаграммы

Можно представить трехмерные (3D) графики, показывающие три термодинамические величины. ^[12]^[13] Например, для одного компонента трехмерный график декартовой координаты может отображать температуру ( T ) на одной оси, давление ( p ) на второй оси и удельный объем ( v ) на третьей. Такой трехмерный график иногда называют p - v - T- диаграммой. Условия равновесия показаны в виде кривых на изогнутой поверхности в 3D с областями для твердой, жидкой и паровой фаз, а также областями, где твердое и жидкое, твердое тело и пар или жидкость и пар сосуществуют в равновесии. Линия на поверхности, называемая тройной линией, — это место, где твердое тело, жидкость и пар могут сосуществовать в равновесии. Критическая точка остается точкой на поверхности даже на трехмерной фазовой диаграмме.

Ортогональная проекция трехмерного графика p – v – T , показывающая давление и температуру по вертикальной и горизонтальной осям, сворачивает трехмерный график в стандартную двумерную диаграмму давления и температуры. Когда это будет сделано, поверхности твердое тело-пар, твердое тело-жидкость и жидкость-пар схлопываются в три соответствующие изогнутые линии, встречающиеся в тройной точке, которая является свернутой ортогональной проекцией тройной линии.

Бинарные смеси

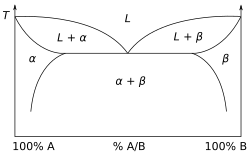
Могут быть построены и другие, гораздо более сложные типы фазовых диаграмм, особенно когда присутствует более одного чистого компонента. В этом случае концентрация становится важной переменной. Могут быть построены фазовые диаграммы с более чем двумя измерениями, которые показывают влияние более чем двух переменных на фазу вещества. Фазовые диаграммы могут использовать другие переменные в дополнение к температуре, давлению и составу или вместо них, например силу приложенного электрического или магнитного поля, а также могут включать вещества, которые принимают более чем три состояния материи.Один тип фазовой диаграммы отображает температуру в зависимости от относительных концентраций двух веществ в бинарной смеси, называемой бинарной фазовой диаграммой , как показано справа. Такая смесь может представлять собой, среди прочего, твердый раствор , эвтектику или перитектику . Эти два типа смесей дают очень разные графики. Другой тип бинарной фазовой диаграммы - это диаграмма температуры кипения смеси двух компонентов, т.е. химические соединения . Для двух конкретных летучих компонентов при определенном давлении, таком как атмосферное давление , диаграмма температуры кипения показывает, какие составы пара (газа) находятся в равновесии с данными составами жидкости в зависимости от температуры. На типичной бинарной диаграмме температуры кипения температура откладывается на вертикальной оси, а состав смеси — на горизонтальной оси.

Показана двухкомпонентная диаграмма с компонентами A и B в «идеальном» растворе. Построение фазовой диаграммы жидкость-пар предполагает наличие идеального жидкого раствора, подчиняющегося закону Рауля , и идеальной газовой смеси, подчиняющейся закону парциального давления Дальтона . Линия, соединяющая жидкость и газ при постоянном давлении, будет указывать на два состава жидкости и газа соответственно. ^[14]

Простой пример диаграммы с гипотетическими компонентами 1 и 2 в неазеотропной смеси показан справа. Тот факт, что существуют две отдельные кривые линии, соединяющие точки кипения чистых компонентов, означает, что состав пара обычно не совпадает с составом жидкости, с которой пар находится в равновесии. см. в разделе «Равновесие пар-жидкость» Дополнительную информацию .

Помимо упомянутых выше типов фазовых диаграмм, существует множество других возможных комбинаций. Некоторые из основных особенностей фазовых диаграмм включают конгруэнтные точки, в которых твердая фаза превращается непосредственно в жидкость. Существует также перитектоид — точка, где две твердые фазы при охлаждении объединяются в одну твердую фазу. Обратное явление, когда одна твердая фаза при охлаждении превращается в две твердые фазы, называется эвтектоидом .

Сложная фазовая диаграмма, имеющая большое технологическое значение, представляет собой диаграмму системы железо - углерод с содержанием углерода менее 7% (см. Сталь ).

Ось X такой диаграммы представляет переменную концентрации смеси. Поскольку смеси обычно далеко не разбавлены, а их плотность как функция температуры обычно неизвестна, предпочтительной мерой концентрации является мольная доля . Измерение объема, такое как молярность , было бы нецелесообразным.

Тройные фазовые диаграммы

Система, состоящая из трех компонентов, называется тройной системой. При постоянном давлении максимальное количество независимых переменных равно трем – температуре и двум значениям концентрации. Для представления тройного равновесия требуется трехмерная фазовая диаграмма. Часто такую диаграмму рисуют с составом в виде горизонтальной плоскости и температурой на оси, перпендикулярной этой плоскости. Для представления композиции в тройной системе используется равносторонний треугольник, называемый треугольником Гиббса (см. также Тройной график ).

Треугольник Гиббса
Пространственная фазовая диаграмма тройной системы

Шкала температур нанесена на оси, перпендикулярной треугольнику состава. Таким образом, пространственная модель тройной фазовой диаграммы представляет собой правотреугольную призму. Стороны призмы представляют соответствующие двойные системы AB, BC, AC.

Однако наиболее распространенными методами представления фазового равновесия в тройной системе являются следующие:1) проекции на концентрационный треугольник АВС поверхностей ликвидуса, солидуса, сольвуса;2) изотермические разрезы;3) вертикальные разрезы. ^[15]

Кристаллы

Полиморфные и полиаморфные вещества имеют множество кристаллических или аморфных фаз, которые можно отобразить на графике так же, как твердые, жидкие и газовые фазы.

Мезофазы

Некоторые органические материалы проходят через промежуточные состояния между твердым и жидким; эти состояния называются мезофазами . Внимание было обращено на мезофазы, поскольку они позволяют использовать устройства отображения и стали коммерчески важными благодаря так называемой жидкокристаллической технологии. Фазовые диаграммы используются для описания возникновения мезофаз. ^[17]

См. также

Ссылки

^ «Фазовые диаграммы» . ch302.cm.utexas.edu . Проверено 14 июля 2023 г.
^ Предель, Бруно; Хох, Майкл младший; Пул, Монте (2004). Фазовые диаграммы и гетерогенные равновесия: практическое введение . Спрингер . ISBN 978-3-540-14011-5 .
^ Папон, П.; Леблон, Дж.; Мейер, PHE (2002). Физика фазового перехода: понятия и приложения . Берлин: Шпрингер. ISBN 978-3-540-43236-4 .
^ Международная ассоциация по свойствам воды и пара «Руководство по использованию фундаментальных физических констант и основных констант воды» , 2001, стр. 5
^ Ландау, Лев Д. ; Лифшиц, Евгений М. (1980). Статистическая физика . Том. 5 (3-е изд.). Баттерворт-Хайнеманн . ISBN 978-0-7506-3372-7 .
^ Перейти обратно: ^а ^б Уиттен, Кеннет В.; Галлей, Кеннет Д.; Дэвис, Раймонд Э. (1992). Общая химия (4-е изд.). Издательство Колледжа Сондерса. п. 477 . ISBN 9780030751561 .
^ Дорин, Генри; Деммин, Питер Э.; Габель, Дороти Л. (1992). Химия: исследование материи Прентис (Четвертое изд.). Прентис Холл . стр. 266–273 . ISBN 978-0-13-127333-7 .
^ Аверилл, Брюс А.; Элдридж, Патрисия (2012). «11.7 Фазовые диаграммы» . Основы общей химии . Креативное сообщество.
^ Петруччи, Ральф Х.; Харвуд, Уильям С.; Херринг, Ф. Джеффри (2002). Общая химия. Принципы и современные приложения (8-е изд.). Прентис Холл. п. 495. ИСБН 0-13-014329-4 .
^ Мукерджи, Гутам Дев; Бёлер, Рейнхард (30 ноября 2007 г.). «Кривая плавления азота при высоком давлении и фазовый переход жидкость-жидкость». Письма о физических отзывах . 99 (22): 225701. Бибкод : 2007PhRvL..99v5701M . doi : 10.1103/PhysRevLett.99.225701 . ПМИД 18233298 .
^ Лейдлер, Кейт Дж.; Мейзер, Джон Х. (1982). Физическая химия . Бенджамин/Каммингс. стр. 173–74.
^ Земански, Марк В.; Диттман, Ричард Х. (1981). Тепло и термодинамика (6-е изд.). МакГроу-Хилл . Рис. 2-3, 2-4, 2-5, 10-10, П10-1. ISBN 978-0-07-072808-0 .
^ Веб-апплет: 3D фазовые диаграммы воды, углекислого газа и аммиака . Описано в Глассер, Лесли; Эрраес, Анхель; Хэнсон, Роберт М. (2009). «Интерактивные трехмерные фазовые диаграммы с использованием Jmol» . Журнал химического образования . 86 (5): 566. Бибкод : 2009ЖЧЭд..86..566Г . дои : 10.1021/ed086p566 . hdl : 20.500.11937/11329 .
^ Дэвид, Карл В. (2022). «Фазовая диаграмма неидеальной смеси p - v - x 2-компонентного представления газ = жидкость, включая азеотропы» . Учебные материалы по химии . Университет Коннектикута . Проверено 9 апреля 2022 г.
^ Алан Принс, «Фазовые равновесия сплавов», Elsevier, 290 стр (1966) ISBN 978-0444404626
^ Похожую диаграмму можно найти на сайте Структура воды и наука. Структура воды и научный сайт Мартина Чаплина, по состоянию на 2 июля 2015 г.
^ Чандрасекхар, Шиварамакришна (1992). Жидкие кристаллы (2-е изд.). Издательство Кембриджского университета . стр. 27–29, 356. ISBN. 978-0-521-41747-1 .

Внешние ссылки

[1] «Фазовые диаграммы» . ch302.cm.utexas.edu . Проверено 14 июля 2023 г.

[2] Предель, Бруно; Хох, Майкл младший; Пул, Монте (2004). Фазовые диаграммы и гетерогенные равновесия: практическое введение . Спрингер . ISBN 978-3-540-14011-5 .

[3] Папон, П.; Леблон, Дж.; Мейер, PHE (2002). Физика фазового перехода: понятия и приложения . Берлин: Шпрингер. ISBN 978-3-540-43236-4 .

[4] Международная ассоциация по свойствам воды и пара «Руководство по использованию фундаментальных физических констант и основных констант воды» , 2001, стр. 5

[5] Ландау, Лев Д. ; Лифшиц, Евгений М. (1980). Статистическая физика . Том. 5 (3-е изд.). Баттерворт-Хайнеманн . ISBN 978-0-7506-3372-7 .

[Whitten-6] Перейти обратно: ^а ^б Уиттен, Кеннет В.; Галлей, Кеннет Д.; Дэвис, Раймонд Э. (1992). Общая химия (4-е изд.). Издательство Колледжа Сондерса. п. 477 . ISBN 9780030751561 .

[Dorin-7] Дорин, Генри; Деммин, Питер Э.; Габель, Дороти Л. (1992). Химия: исследование материи Прентис (Четвертое изд.). Прентис Холл . стр. 266–273 . ISBN 978-0-13-127333-7 .

[8] Аверилл, Брюс А.; Элдридж, Патрисия (2012). «11.7 Фазовые диаграммы» . Основы общей химии . Креативное сообщество.

[9] Петруччи, Ральф Х.; Харвуд, Уильям С.; Херринг, Ф. Джеффри (2002). Общая химия. Принципы и современные приложения (8-е изд.). Прентис Холл. п. 495. ИСБН 0-13-014329-4 .

[Muk007-10] Мукерджи, Гутам Дев; Бёлер, Рейнхард (30 ноября 2007 г.). «Кривая плавления азота при высоком давлении и фазовый переход жидкость-жидкость». Письма о физических отзывах . 99 (22): 225701. Бибкод : 2007PhRvL..99v5701M . doi : 10.1103/PhysRevLett.99.225701 . ПМИД 18233298 .

[11] Лейдлер, Кейт Дж.; Мейзер, Джон Х. (1982). Физическая химия . Бенджамин/Каммингс. стр. 173–74.

[12] Земански, Марк В.; Диттман, Ричард Х. (1981). Тепло и термодинамика (6-е изд.). МакГроу-Хилл . Рис. 2-3, 2-4, 2-5, 10-10, П10-1. ISBN 978-0-07-072808-0 .

[13] Веб-апплет: 3D фазовые диаграммы воды, углекислого газа и аммиака . Описано в Глассер, Лесли; Эрраес, Анхель; Хэнсон, Роберт М. (2009). «Интерактивные трехмерные фазовые диаграммы с использованием Jmol» . Журнал химического образования . 86 (5): 566. Бибкод : 2009ЖЧЭд..86..566Г . дои : 10.1021/ed086p566 . hdl : 20.500.11937/11329 .

[14] Дэвид, Карл В. (2022). «Фазовая диаграмма неидеальной смеси p - v - x 2-компонентного представления газ = жидкость, включая азеотропы» . Учебные материалы по химии . Университет Коннектикута . Проверено 9 апреля 2022 г.

[15] Алан Принс, «Фазовые равновесия сплавов», Elsevier, 290 стр (1966) ISBN 978-0444404626

[16] Похожую диаграмму можно найти на сайте Структура воды и наука. Структура воды и научный сайт Мартина Чаплина, по состоянию на 2 июля 2015 г.

[17] Чандрасекхар, Шиварамакришна (1992). Жидкие кристаллы (2-е изд.). Издательство Кембриджского университета . стр. 27–29, 356. ISBN. 978-0-521-41747-1 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

v т и Химическое равновесие
Concepts	Chemical stability Chelation Dynamic equilibrium Equilibrium chemistry Equilibrium stage Free energy Gibbs Helmholtz Le Chatelier's principle Phase separation Reversible reaction Thermodynamic equilibrium
Models	Equilibrium constant determination Phase diagram Predominance diagram Phase rule Reaction quotient Thermodynamic activity
Applications	Buffer solution Equilibrium unfolding Liquid–liquid extraction
Specific equilibria	Acid dissociation Hammett acidity function Binding constant Binding selectivity Coordination complexes Macrocyclic effect Dissociation constant Hydrolysis Self-ionization of water Partition Distribution coefficient Solubility Common-ion effect Vapor–liquid Henry's law

v т и Химические растворы
Solution	Ideal solution Aqueous solution Solid solution Buffer solution Flory–Huggins Mixture Suspension Colloid Phase diagram Phase separation Eutectic point Alloy Saturation Supersaturation Serial dilution Dilution (equation) Apparent molar property Miscibility gap
Concentration and related quantities	Molar concentration Mass concentration Number concentration Volume concentration Normality Molality Mole fraction Mass fraction Isotopic abundance Mixing ratio Ternary plot
Solubility	Solubility equilibrium Total dissolved solids Solvation Solvation shell Enthalpy of solution Lattice energy Raoult's law Henry's law Solubility table (data) Solubility chart Miscibility
Solvent	(Category) Acid dissociation constant Protic solvent Polar aprotic solvent Inorganic nonaqueous solvent Solvation List of boiling and freezing information of solvents Partition coefficient Polarity Hydrophobe Hydrophile Lipophilic Amphiphile Lyonium ion Lyate ion