Объект натуральных чисел

В теории категорий объект натуральных чисел ( NNO ) — это объект, наделенный рекурсивной структурой , аналогичной натуральным числам . Точнее, в категории E с конечным объектом 1 NNO N определяется следующим образом:

глобальный элемент z : 1 → N и
стрелка s : N → N ,

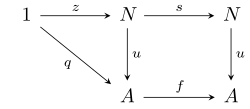
такой, что для любого объекта A из E , глобального элемента q : 1 → A и стрелки f : A → A существует единственная стрелка u : N → A такая, что:

ты ∘ z знак равно q и
ты ∘ s знак равно ж ∘ ты . ^[1]^[2]^[3]

Другими словами, треугольник и квадрат на следующей диаграмме коммутируют.

Пару ( q , f ) иногда называют данными рекурсии для u , заданными в форме рекурсивного определения :

⊢ ты ( z ) знак равно q
y ∈ _E N ⊢ ты ( s y ) знак равно ж ( ты ( y ))

Приведенное выше определение является универсальным свойством NNO, то есть они определены с точностью до канонического изоморфизма . Если стрелка u, определенная выше, просто должна существовать, то есть уникальность не требуется, то N называется слабым NNO.

определения Эквивалентные

NNO в декартовых замкнутых категориях (CCC) или топосах иногда определяются следующим эквивалентным способом (по Лоуверу ): для каждой пары стрелок g : A → B и f : B → B существует уникальный h : N × A. → B такой, что квадраты на следующей диаграмме коммутируют. ^[4]

Эта же конструкция определяет слабые NNO в декартовых категориях, которые не являются декартово замкнутыми.

В категории с терминальным объектом 1 и бинарными копроизведениями (обозначаемыми +) NNO можно определить как начальную алгебру эндофунктора , который действует на объекты посредством $X \mapsto 1 + X$ и на стрелки посредством $f \mapsto id 1 + f$ . ^[5]

Свойства [ править ]

Каждое ННО является исходным объектом категории диаграмм вида

1{\xrightarrow {~\quad q\quad ~}}A{\xrightarrow {~\quad f\quad ~}}A

Если в декартовой замкнутой категории есть слабые NNO, то в каждом ее фрагменте также есть слабые NNO.
ННО можно использовать для нестандартных моделей теории типов аналогично нестандартным моделям анализа. Такие категории (или топосы), как правило, имеют «бесконечное количество» нестандартных натуральных чисел. ^{[ нужны разъяснения ]} (Как всегда, есть простые способы получить нестандартные NNO; например, если z = sz , в этом случае категория или топос E тривиальна.)
Фрейд показал, что z и s образуют диаграмму копродукции для NNO; также, ! _N : N является коэквалайзером s → 1 и 1 _N , т. е . каждая пара глобальных элементов N соединена посредством s ; более того, эта пара фактов характеризует все ННО.

Примеры [ править ]

В Set , категории множеств , стандартные натуральные числа являются NNO. ^[6] Терминальный объект в Set — это синглтон , а функция из синглтона выбирает один элемент набора. Натуральные числа 𝐍 представляют собой NNO, где z — функция от одноэлементного числа до 𝐍, образ которой равен нулю, а s — функция-преемник . (На самом деле мы могли бы позволить z выбрать любой элемент из 𝐍, и полученное NNO было бы изоморфно этому.) Можно доказать, что диаграмма в определении коммутирует, используя математическую индукцию .
В категории типов теории типов Мартина-Лёфа (с типами как объектами и функциями как стрелками) стандартный тип натуральных чисел nat является NNO. Можно использовать рекурсор для nat , чтобы показать, что соответствующая диаграмма коммутирует.
Предположим, что ${\mathcal {E}}$ представляет собой топос Гротендика с конечным объектом $\top$ и это ${\mathcal {E}}\simeq \mathbf {Shv} ({\mathfrak {C}},J)$ для некоторой топологии Гротендика $J$ по категории ${\mathfrak {C}}$ . Тогда, если $\Gamma _{\mathbb {N} }$ постоянный предпучок на ${\mathfrak {C}}$ , то ННО в ${\mathcal {E}}$ это снопирование $\Gamma _{\mathbb {N} }$ и может быть показано, что он принимает форму $\mathbb {N} _{\mathcal {E}}\cong \left(\Gamma _{\mathbb {N} }\right)^{++}\cong \coprod _{n\in \mathbb {N} }\top .$

См. также [ править ]

Пеано арифметики Аксиомы
Категорическая логика

Ссылки [ править ]

^ Джонстон 2002 , A2.5.1.
^ Ловере 2005 , с. 14.
^ Ленстер, Том (2014). «Переосмысление теории множеств». Американский математический ежемесячник . 121 (5): 403–415. arXiv : 1212.6543 . Бибкод : 2012arXiv1212.6543L . doi : 10.4169/amer.math.monthly.121.05.403 . S2CID 5732995 .
^ Джонстон 2002 , A2.5.2.
^ Барр, Майкл; Уэллс, Чарльз (1990). Теория категорий для информатики . Нью-Йорк: Прентис Холл. п. 358. ИСБН 0131204866 . OCLC 19126000 .
^ Джонстон 2005 , с. 108.

Джонстон, Питер Т. (2002). Зарисовки слона: сборник теории топоса . Оксфорд: Издательство Оксфордского университета. ISBN 0198534256 . OCLC 50164783 .
Ловер, Уильям (2005) [1964]. «Элементарная теория категории множеств (длинная версия) с комментарием» . Переиздания по теории и приложениям категорий . 11 :1–35.

Внешние ссылки [ править ]

Конспекты лекций Роберта Харпера , в которых обсуждаются ННО в разделе 2.2: https://www.cs.cmu.edu/~rwh/courses/hott/notes/notes_week3.pdf
Сообщение в блоге Клайва Ньюстеда о кафе n -Category: https://golem.ph.utexas.edu/category/2014/01/an_elementary_theory_of_the_ca.html.
Заметки о типах данных как алгебрах для эндофункторов ученого-компьютерщика Филипа Вадлера : http://homepages.inf.ed.ac.uk/wadler/papers/free-rectypes/free-rectypes.txt
Примечания к nLab : https://ncatlab.org/nlab/show/ETCS .

[FOOTNOTEJohnstone2002A2.5.1-1] Джонстон 2002 , A2.5.1.

[FOOTNOTELawvere200514-2] Ловере 2005 , с. 14.

[3] Ленстер, Том (2014). «Переосмысление теории множеств». Американский математический ежемесячник . 121 (5): 403–415. arXiv : 1212.6543 . Бибкод : 2012arXiv1212.6543L . doi : 10.4169/amer.math.monthly.121.05.403 . S2CID 5732995 .

[FOOTNOTEJohnstone2002A2.5.2-4] Джонстон 2002 , A2.5.2.

[5] Барр, Майкл; Уэллс, Чарльз (1990). Теория категорий для информатики . Нью-Йорк: Прентис Холл. п. 358. ИСБН 0131204866 . OCLC 19126000 .

[FOOTNOTEJohnstone2005108-6] Джонстон 2005 , с. 108.

[1]

[2]

[3]

[4]

[5]

[6]

определения Эквивалентные ​ ​