Спираль Бурдейка – Кокстера

Спирали Кокстера из правильных тетраэдров

Поворот против и по часовой стрелке
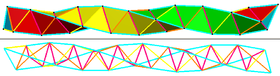Края можно раскрасить в 6 групп: 3 основные спирали (голубые), при этом вогнутые края образуют медленную прямую спираль (пурпурный) и две обратные спирали (желтую и оранжевую). ^[1]

Спираль Бурдейка -Коксетера , названная в честь HSM Coxeter и Ари Хендрика Бурдейка [ es ] , представляет собой линейную стопку правильных тетраэдров , расположенных так, что ребра комплекса, принадлежащие только одному тетраэдру, образуют три переплетающиеся спирали . Существуют две киральные формы: с обмотками по часовой стрелке или против часовой стрелки. В отличие от любой другой стопки платоновых тел , спираль Бурдейка-Коксетера не является повторяющейся во вращении в трехмерном пространстве. Даже в бесконечной цепочке сложенных друг на друга тетраэдров никакие два тетраэдра не будут иметь одинаковую ориентацию, поскольку шаг спирали на ячейку не является рациональной частью круга. Однако были обнаружены модифицированные формы этой спирали, повторяющиеся во вращении. ^[2] и в 4-мерном пространстве эта спираль повторяется в кольцах ровно из 30 тетраэдрических ячеек, которые мозаично образуют 3-сферную поверхность 600-ячеистой , одной из шести правильных выпуклых полихор .

Бакминстер Фуллер назвал их тетраспиралями и считал их правильными и неправильными тетраэдрическими элементами. ^[3]

Геометрия

Координаты вершин спирали Бурдейка–Коксетера, составленной из тетраэдров с единичной длиной ребра, можно записать в виде

(r\cos n\theta ,r\sin n\theta ,nh)

где $r=3{\sqrt {3}}/10$ , $\theta =\pm \cos ^{-1}(-2/3)\approx 131.81^{\circ }$ , $h=1/{\sqrt {10}}$ и $n$ является произвольным целым числом. Два разных значения $\theta$ соответствуют двум хиральным формам. Все вершины расположены на цилиндре радиусом $r$ вдоль оси z. Учитывая, как чередуются тетраэдры, это дает очевидный поворот в $2\theta -{\frac {4}{3}}\pi \approx 23.62^{\circ }$ каждые два тетраэдра. Имеется еще один вписанный цилиндр радиусом $3{\sqrt {2}}/20$ внутри спирали. ^[4]

Многомерная геометрия

разделены 600 ячеек на 20 колец по 30 тетраэдров , каждое из которых представляет собой спираль Бурдейка – Коксетера. ^[5] При наложении на кривизну трехсферы она становится периодической с периодом в десять вершин, охватывающей все 30 ячеек. Совокупность таких спиралей в 600-ячейке представляет собой дискретное расслоение Хопфа . ^[6] В то время как в трехмерном измерении края представляют собой спирали, в наложенной трехсферной топологии они являются геодезическими и не имеют кручения . Они естественным образом закручиваются вокруг друг друга из-за расслоения Хопфа. ^[7] Коллектив ребер образует еще одно дискретное расслоение Хопфа из 12 колец по 10 вершин каждое. Они соответствуют кольцам из 10 додекаэдров в двойном 120-ячеечном .

Кроме того, 16-ячеечные разбиваются на два кольца 8-тетраэдра длиной в четыре ребра, а 5-ячеечные разбиваются на одно вырожденное кольцо 5-тетраэдра .

4-многогранник	Кольца	Тетраэдры/кольцо	Длина цикла
600-ячеечный	20	30	30, 10 ³, 15 ²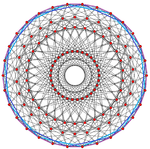
16-ячеечный	2	8	8, 8, 4 ²
5-клеточный	1	5	(5, 5), 5

Родственные многогранные спирали

Равносторонние квадратные пирамиды также могут быть соединены в спираль с двумя конфигурациями вершин : 3.4.3.4 и 3.3.4.3.3.4. Эта спираль существует как конечное кольцо из 30 пирамид в 4-мерном многограннике .

А равносторонние пятиугольные пирамиды могут быть объединены в цепочки с тремя конфигурациями вершин: 3.3.5, 3.5.3.5 и 3.3.3.5.3.3.5:

В архитектуре

Art Tower Mito основана на спирали Бурдейка-Коксетера.

См. также

Примечания

^ Садок и Ривьер 1999 , с. 314, §4.2.2 Спираль Бурдейка-Коксетера и спираль PPII; спираль тетраэдров встречается в форме левой или правой спирали, но каждая форма содержит как левую, так и правую спиральные спирали связанных ребер.
^ Сэдлер и др. 2013 .
^ Фуллер 1975 , 930.00 Тетраспираль .
^ «Данные Тетраспирали» .
^ Sadoc 2001 , стр. 577–578, §2.5 Симметрия 30/11: пример другого вида симметрии.
^ Банчофф 2013 , изучил разложение правильных 4-многогранников на соты торов, покрывающих тор Клиффорда , которые соответствуют расслоениям Хопфа .
^ Банчофф 1988 .

Ссылки

Коксетер, HSM (1974). Правильные комплексные многогранники . Издательство Кембриджского университета. ISBN 052120125X .
Бурдейк, АХ (1952). «Некоторые замечания по поводу плотной упаковки равных сфер». Филипс Рез. Представитель . 7 : 303–313.
Фуллер, Р. Бакминстер (1975). Эпплуайт, Э.Дж. (ред.). Синергетика . Макмиллан.
Пью, Энтони (1976). «5. Соединение многогранников §5.36 Тетраспираль». Многогранники: визуальный подход . Издательство Калифорнийского университета. п. 53. ИСБН 978-0-520-03056-5 .
Сэдлер, Гарретт; Клык, Клык; Ковач, Хулио; Клее, Ирвин (2013). «Периодическая модификация спирали Бурдейка-Коксетера (тетраспирали)». arXiv : 1302.1174v1 [ math.MG ].
Лорд, Э.А.; Ранганатан, С. (2004). «Структура γ-латуни и спираль Бурдейка – Кокстера» (PDF) . Журнал некристаллических твердых тел . 334–335: 123–5. Бибкод : 2004JNCS..334..121L . дои : 10.1016/j.jnoncrysol.2003.11.069 .
Хуан, Цзяньфэн; Лю, Чен, Хан, Ю (2014) Чжу , . Ихан; Шан, Чэн ; Am Chem . 136 (36): 12746–52. : / ja506554j . 10.1021 документа Номер
Лорд, Эрик А.; Маккей, Алан Л.; Ранганатан, С. (2006). «§4.5 Спираль Бурдейка – Кокстера» . Новая геометрия для новых материалов . Издательство Кембриджского университета. п. 64. ИСБН 978-0-521-86104-5 .
Банчофф, Томас Ф. (1988). «Геометрия отображения Хопфа и торы Пинкала заданного конформного типа». В Тангоре, Мартин (ред.). Компьютеры в алгебре . Нью-Йорк и Базель: Марсель Деккер. стр. 57–62.
Банчофф, Томас Ф. (2013). «Разложения тора правильных многогранников в 4-мерном пространстве». В Сенешале, Марджори (ред.). Формирование пространства . Спрингер Нью-Йорк. стр. 257–266 . дои : 10.1007/978-0-387-92714-5_20 . ISBN 978-0-387-92713-8 .
Садок, Дж. Ф.; Ривье, Н. (1999). «Спираль Бурдейка-Коксетера и биологические спирали». Европейский физический журнал Б. 12 (2): 309–318. Бибкод : 1999EPJB...12..309S . дои : 10.1007/s100510051009 . S2CID 92684626 .
Садок, Жан-Франсуа (2001). «Спирали и спиральные упаковки, полученные из многогранника {3,3,5}» . Европейский физический журнал E. 5 : 575–582. дои : 10.1007/s101890170040 . S2CID 121229939 .

Внешние ссылки

[FOOTNOTESadocRivier1999314§4.2.2_The_Boerdijk-Coxeter_helix_and_the_PPII_helix-1] Садок и Ривьер 1999 , с. 314, §4.2.2 Спираль Бурдейка-Коксетера и спираль PPII; спираль тетраэдров встречается в форме левой или правой спирали, но каждая форма содержит как левую, так и правую спиральные спирали связанных ребер.

[FOOTNOTESadlerFangKovacsKlee2013-2] Сэдлер и др. 2013 .

[FOOTNOTEFuller1975[httpwwwrwgrayprojectscomsynergeticss09p3000html_930.00_Tetrahelix]-3] Фуллер 1975 , 930.00 Тетраспираль .

[4] «Данные Тетраспирали» .

[FOOTNOTESadoc2001577–578§2.5_The_30/11_symmetry:_an_example_of_other_kind_of_symmetries-5] Sadoc 2001 , стр. 577–578, §2.5 Симметрия 30/11: пример другого вида симметрии.

[FOOTNOTEBanchoff2013-6] Банчофф 2013 , изучил разложение правильных 4-многогранников на соты торов, покрывающих тор Клиффорда , которые соответствуют расслоениям Хопфа .

[FOOTNOTEBanchoff1988-7] Банчофф 1988 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]