Генерация сетки

Генерация сетки — это практика создания сетки , разделения непрерывного геометрического пространства на дискретные геометрические и топологические ячейки.Часто эти клетки образуют симплициальный комплекс .Обычно ячейки разделяют геометрическую входную область.Ячейки сетки используются как дискретные локальные аппроксимации более крупной области. Сетки создаются с помощью компьютерных алгоритмов, часто под руководством человека через графический интерфейс , в зависимости от сложности предметной области и желаемого типа сетки.Типичная цель — создать сетку, которая точно отражает геометрию входной области, с ячейками высокого качества (правильной формы) и без такого большого количества ячеек, которые затрудняли бы последующие вычисления.Сетка также должна быть мелкой (иметь мелкие элементы) в областях, важных для последующих расчетов.

Сетки используются для рендеринга на экране компьютера и для физического моделирования, такого как анализ методом конечных элементов или вычислительная гидродинамика . Сетки состоят из простых ячеек, таких как треугольники, потому что, например, мы знаем, как выполнять такие операции, как вычисления методом конечных элементов (инженерия) или трассировка лучей (компьютерная графика) на треугольниках, но мы не знаем, как выполнять эти операции непосредственно на сложных пространствах. и формы, такие как проезжий мост. Мы можем моделировать прочность моста или нарисовать его на экране компьютера, выполняя расчеты для каждого треугольника и рассчитывая взаимодействия между треугольниками.

Основное различие между структурированной и неструктурированной сеткой. В структурированной сетке сетка представляет собой регулярную решетку, например массив, с подразумеваемой связностью между элементами. В неструктурированной сетке элементы могут быть соединены друг с другом нерегулярным образом, и можно захватывать более сложные области. Эта страница в первую очередь посвящена неструктурированным сеткам.Хотя сетка может представлять собой триангуляцию , процесс создания сетки отличается от триангуляции набора точек тем, что создание сетки включает в себя свободу добавления вершин, отсутствующих во входных данных. «Фасетирование» (триангуляция) моделей САПР для черчения имеет такую же свободу добавления вершин, но цель состоит в том, чтобы точно представить форму, используя как можно меньше треугольников, а форма отдельных треугольников не важна. Вместо этого при компьютерной графике рендеринга текстур и реалистичных условий освещения используются сетки.

Многие программы для создания сеток связаны с системой САПР, определяющей входные данные, и программным обеспечением для моделирования, принимающим выходные данные. Входные данные могут сильно различаться, но распространенными формами являются твердотельное моделирование , геометрическое моделирование , NURBS , B-rep , STL или облако точек .

Терминология

Термины « генерация сетки », « генерация сетки», « построение сетки » и « построение сетки » часто используются как взаимозаменяемые, хотя, строго говоря, последние два являются более широкими и охватывают улучшение сетки: изменение сетки с целью увеличения скорости или точность числовых вычислений, которые будут выполняться над ней. В рендеринге компьютерной графики и математике сетку иногда называют тесселяцией .

Грани сетки (ячейки, объекты) имеют разные имена в зависимости от их размера и контекста, в котором сетка будет использоваться. В конечных элементах объекты сетки высшей размерности называются «элементами», «ребра» — 1D, а «узлы» — 0D. Если элементы трехмерные, то двухмерные объекты являются «лицами». В вычислительной геометрии точки 0D называются вершинами. Тетраэдры часто называют «тетами»; треугольники — это «трисы», четырехугольники — «четырехугольники», а шестигранники (топологические кубы) — «шестигранники».

Техники

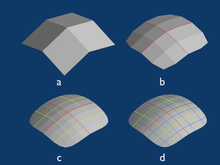
Многие методы построения сетки построены на принципах триангуляции Делоне вместе с правилами добавления вершин, такими как алгоритм Руперта .Отличительной особенностью является то, что формируется первоначальная грубая сетка всего пространства, затем добавляются вершины и треугольники.Напротив, продвинутые фронтальные алгоритмы начинают с границы области и добавляют элементы, постепенно заполняющие внутреннюю часть. Гибридные методы делают и то, и другое. Особый класс передовых фронтальных техник создает тонкие пограничные слои элементов для потока жидкости.При создании структурированной сетки вся сетка представляет собой решетчатый граф , например регулярную сетку квадратов. При построении сетки с блочной структурой область делится на большие подобласти, каждая из которых представляет собой структурированную сетку. Некоторые прямые методы начинаются с сетки с блочной структурой, а затем перемещают сетку в соответствии с входными данными; см. Автоматическое создание шестнадцатеричной сетки на основе поликуба . Другой прямой метод — разрезать структурированные ячейки по границе домена; см . лепку на основе Марширующие кубики .

Некоторые типы сеток создать гораздо сложнее, чем другие. Симплициальные сетки обычно проще кубических. Важной категорией является создание шестигранной сетки, соответствующей фиксированной четырехугольной поверхностной сетке; Подобласть исследований изучает существование и генерацию сеток конкретных малых конфигураций, таких как тетрагональный трапецоэдр . Из-за сложности этой проблемы существование комбинаторных шестигранных сеток изучалось отдельно от проблемы генерации хороших геометрических реализаций. Хотя известные алгоритмы генерируют симплициальные сетки с гарантированным минимальным качеством, такие гарантии редки для кубических сеток, и многие популярные реализации генерируют перевернутые (вывернутые наизнанку) шестиугольники из некоторых входных данных.

Сетки часто создаются последовательно на рабочих станциях, даже если последующие вычисления над сеткой будут выполняться параллельно на суперкомпьютерах. Это связано как с ограничением, заключающимся в том, что большинство генераторов сеток являются интерактивными, так и с тем, что время выполнения генерации сетки обычно незначительно по сравнению со временем решателя. Однако, если сетка слишком велика, чтобы поместиться в памяти одной серийной машины, или сетка должна быть изменена (адаптирована) в ходе моделирования, построение сетки выполняется параллельно.

Алгебраические методы

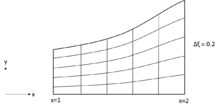
Построение сетки алгебраическими методами основано на математической интерполяционной функции . Это делается с использованием известных функций в одном, двух или трех измерениях, занимающих области произвольной формы. Расчетная область может быть не прямоугольной, но для простоты она считается прямоугольной. Основное преимущество этих методов состоит в том, что они обеспечивают явный контроль формы и шага физической сетки. Простейшей процедурой, которую можно использовать для создания расчетной сетки, подходящей по границам, является преобразование нормализации. ^[1]
Для насадки с описывающей функцией $y=x^{2}$ сетку можно легко создать, используя равномерное деление в направлении y с равноотстоящими приращениями в направлении x , которые описываются формулой

\xi =x\,

\eta ={\frac {y}{y_{\max }}}\,

где $y_{\max }$ обозначает координату Y стенки сопла. Для заданных значений ( $\xi$ , $\eta$ ), значения ( $x$ , $y$ ) можно легко восстановить.

Методы дифференциальных уравнений

Как и алгебраические методы, методы дифференциальных уравнений также используются для создания сеток. Преимущество использования уравнений в частных производных (УЧП) заключается в том, что решение уравнений, создающих сетку, можно использовать для создания сетки. Построение сетки может быть выполнено с использованием всех трех классов уравнений в частных производных .

Эллиптические схемы

Эллиптические УЧП обычно имеют очень гладкие решения, ведущие к гладким контурам. Используя его гладкость как преимущество, уравнения Лапласа предпочтительно использовать , поскольку якобиан оказался положительным в результате принципа максимума для гармонических функций . После обширной работы, проделанной Кроули (1962) и Уинслоу (1966) ^[2] на PDE путем преобразования физической области в вычислительную плоскость при отображении с использованием уравнения Пуассона , Томпсон и др. (1974) ^[3] много работали над эллиптическими УЧП для создания сеток. В генераторах сетки Пуассона отображение осуществляется путем маркировки нужных точек сетки. $(x,y)$ на границе физической области, при этом распределение внутренних точек определяется решением уравнений, записанных ниже

\xi _{xx}+\xi _{yy}=P(\xi ,\eta )

\eta _{xx}+\eta _{yy}=Q(\xi ,\eta )

где, $(\xi ,\eta )$ являются координатами в вычислительной области, а P и Q отвечают за расстояние между точками внутри D. Преобразование приведенных выше уравнений в вычислительном пространстве дает набор из двух эллиптических УЧП формы:

\alpha x_{\xi \xi }-2\beta x_{\xi \eta }+\gamma x_{\eta \eta }=-I^{2}(Px_{\xi }+Qx_{\eta })

\alpha y_{\xi \xi }-2\beta y_{\xi \eta }+\gamma y_{\eta \eta }=-I^{2}(Py_{\xi }+Qy_{\eta })

где

{\begin{aligned}\alpha &=x_{\eta }^{2}+y_{\eta }^{2}\\\beta &=x_{\eta }x_{\xi }+y_{\xi }y_{\eta }\\\gamma &=x_{\xi }^{2}+y_{\xi }^{2}\\I&={\frac {\delta (x,y)}{\delta (\xi ,\eta )}}=y_{\eta }x_{\xi }-y_{\xi }x_{\eta }\end{aligned}}

Эти системы уравнений решаются в вычислительной плоскости на равномерной сетке, что дает нам $(x,y)$ координаты каждой точки физического пространства. Преимущество использования эллиптических УЧП заключается в том, что связанное с ними решение является гладким, а результирующая сетка — гладкой. Но спецификация P и Q становится сложной задачей, что добавляет ей недостатков. Более того, сетку необходимо рассчитывать после каждого временного шага, что увеличивает время вычислений. ^[4]

Гиперболические схемы

Эта схема построения сетки обычно применима к задачам с открытыми областями, соответствующими типу УЧП, описывающему физическую проблему. Преимущество гиперболических УЧП заключается в том, что для создания сетки необходимо решать основные уравнения только один раз. Начальное распределение точек вместе с приблизительными граничными условиями формирует необходимые входные данные, а затем решение выводится наружу. Стегер и Соренсон (1980) ^[5] предложил метод объемной ортогональности, который использует гиперболические PDE для создания сетки.Для двумерной задачи, учитывая вычислительное пространство, определяемое формулой $\Delta \xi =\Delta \eta =1$ обратная якобиана определяется формулой:

x_{\xi }y_{\eta }-x_{\eta }y_{\xi }=I

где $I$ представляет площадь в физическом пространстве для данной области в вычислительном пространстве. Второе уравнение связывает ортогональность линий сетки на границе физического пространства, которую можно записать как

d\xi =0=\xi _{x}\,dx+\xi _{y}\,dy.

Для $\xi$ и $\eta$ если поверхности перпендикулярны, уравнение принимает вид

x_{\xi }x_{\eta }+y_{\xi }y_{\eta }=0.

Проблема, связанная с такой системой уравнений, заключается в задании $I$ . Плохой выбор $I$ может привести к шоку и прерывистому распространению этой информации по сетке. Несмотря на то, что сетка ортогональна, она генерируется очень быстро, что является преимуществом этого метода.

Параболические схемы

Техника решения аналогична методике гиперболических УЧП : решение продвигается от исходной поверхности данных, удовлетворяющей граничным условиям в конце. Накамура (1982) и Эдвардс (1985) разработали основные идеи построения параболических сеток. Идея использует либо уравнение Лапласа , либо уравнение Пуассона , особенно рассматривая части, которые контролируют эллиптическое поведение. Начальные значения задаются как координаты точки вдоль поверхности. $\eta =0$ и продвижение решений к внешней поверхности объекта, удовлетворяющего граничным условиям, вдоль $\xi$ края.

Управление шагом сетки до сих пор не предлагалось. Накамура и Эдвардс, управление сеткой осуществлялось с использованием неравномерного интервала. Построение параболической сетки демонстрирует преимущество перед генерацией гиперболической сетки, заключающееся в том, что не происходит никаких потрясений или разрывов, и сетка является относительно гладкой. Однако определение начальных значений и выбор размера шага для управления точками сетки отнимает много времени, но эти методы могут быть эффективными при наличии знаний и опыта.

Вариационные методы

Этот метод включает в себя технику, которая минимизирует гладкость сетки , ортогональность и изменение объема. Этот метод формирует математическую платформу для решения задач построения сеток. В этом методе альтернативная сетка генерируется с помощью новой сетки после каждой итерации и вычисления скорости сетки с использованием метода обратной разности . Этот метод является мощным, но его недостатком является то, что для решения уравнений, связанных с сеткой, требуются усилия. Необходимо провести дальнейшую работу по минимизации интегралов , которые уменьшат время процессора.

Генерация неструктурированной сетки

Основная важность этой схемы заключается в том, что она предоставляет метод, который автоматически генерирует сетку. Используя этот метод, сетки сегментируются на блоки в соответствии с поверхностью элемента и создается структура, обеспечивающая соответствующую связность. данных Для интерпретации потока используется решатель. При использовании неструктурированной схемы основной целью является удовлетворение требований пользователя, и для выполнения этой задачи используется генератор сетки. Хранение информации в структурированной схеме происходит от ячейки к ячейке, а не от сетки к сетке, и, следовательно, требуется больше места в памяти. решателя Из-за случайного расположения ячеек эффективность в неструктурированной схеме меньше по сравнению со структурированной схемой. ^[6]

Некоторые моменты необходимо учитывать во время построения сетки . Точка сетки с высоким разрешением создает трудности как для структурированных, так и для неструктурированных. Например, в случае пограничного слоя структурированная схема создает вытянутую сетку по направлению потока. С другой стороны, неструктурированные сетки требуют более высокой плотности ячейка должна быть как можно более равносторонней . ячеек в пограничном слое, поскольку во избежание ошибок ^[7]

Мы должны определить, какая информация необходима для идентификации ячейки и всех соседей ячейки в вычислительной сетке. Мы можем разместить произвольные точки в любом месте неструктурированной сетки. Схема вставки точек используется для независимой вставки точек и определения связности ячеек. Это предполагает, что точки будут идентифицированы по мере их вставки. Логика установления нового соединения определяется после вставки точек. Необходимы данные, которые формируют точку сетки, которая идентифицирует ячейку сетки. По мере формирования каждая ячейка нумеруется, а точки сортируются. Кроме того, необходима информация о соседней ячейке.

Адаптивная сетка

Проблема при решении уравнений в частных производных с использованием предыдущих методов заключается в том, что сетка строится и точки распределяются в физической области до того, как становятся известны детали решения. Таким образом, сетка может быть, а может и не быть лучшей для данной задачи. ^[8]

Адаптивные методы используются для повышения точности решений. Адаптивный метод называется методом «h», если используется измельчение сетки, методом «r», если количество точек сетки фиксировано и не перераспределяется, и «p», если порядок схемы решения увеличивается в теории конечных элементов. Многомерные задачи с использованием схемы равнораспределения можно решить несколькими способами. Самыми простыми для понимания являются генераторы сетки Пуассона с функцией управления, основанной на равнораспределении весовой функции с диффузией , кратной желаемому объему ячейки. Схема равнораспределения также может быть применена к неструктурированной задаче. Проблема в том, что связность затрудняется, если перемещение точек сетки очень велико.

Устойчивый поток и расчет расхода с точностью по времени могут быть решены с помощью этого адаптивного метода. Сетка уточняется после заранее определенного количества итераций, чтобы адаптировать ее к задаче об устойчивом потоке. Сетка перестанет подстраиваться под изменения, как только решение сойдётся. В точном по времени случае связь дифференциальных уравнений в частных производных требуется физической задачи и уравнений, описывающих движение сетки.

Создание сетки на основе изображений

Создание сетки на основе изображений — это автоматизированный процесс создания компьютерных моделей для вычислительной гидродинамики (CFD) и анализа методом конечных элементов (FEA) на основе данных трехмерных изображений (таких как магнитно-резонансная томография (МРТ), компьютерная томография (КТ) или микротомография . Хотя в настоящее время доступен широкий спектр методов создания сеток, они обычно разрабатываются для создания моделей с помощью компьютерного проектирования (САПР), и поэтому возникают трудности с построением сетки на основе данных трехмерного изображения.

Топология ячейки

Обычно ячейки имеют многоугольную или многогранную форму и образуют сетку , разделяющую домен.Важные классы двумерных элементов включают треугольники (симплексы) и четырехугольники (топологические квадраты).В трехмерных измерениях наиболее распространенными ячейками являются тетраэдры (симплексы) и шестигранники (топологические кубы). Симплициальные сетки могут иметь любую размерность и в качестве важных примеров включают треугольники (2D) и тетраэдры (3D). Кубические сетки — это пан-мерная категория, включающая четырехугольники (2D) и шестиугольники (3D). В 3D четырехсторонние пирамиды и трехсторонние призмы появляются в конформных сетках смешанного типа ячеек.

Размер ячейки

Сетка встроена в геометрическое пространство, которое обычно является двух- или трехмерным , хотя иногда размерность увеличивается на единицу путем добавления измерения времени. Сетки более высокой размерности используются в нишевых контекстах. Одномерные сетки также полезны. Важной категорией являются поверхностные сетки, которые представляют собой 2D-сетки, встроенные в 3D для представления изогнутой поверхности.

Двойственность

Двойные графы играют несколько ролей в сетке. Можно создать сетку многогранной диаграммы Вороного , дуализовав симплициальную триангуляционную сетку Делоне . Можно создать кубическую сетку, создав расположение поверхностей и дуализировав граф пересечений; см. пространственный поворот континуума . Иногда в одной симуляции используются как основная сетка, так и ее двойная сетка; см . звездный оператор Ходжа . Это возникает из физики, включающей операторы дивергенции и ротора (математические) , такие как поток и завихрение или электричество и магнетизм , где одна переменная естественным образом живет на основных гранях, а ее аналог на двойных гранях.

Тип сетки по использованию

Трехмерные сетки, созданные для анализа методом конечных элементов, должны состоять из тетраэдров , пирамид , призм или шестигранников . Те, которые используются для метода конечных объемов, могут состоять из произвольных многогранников . Те, которые используются для методов конечных разностей, состоят из кусочно структурированных массивов шестигранников, известных как многоблочные структурированные сетки. Четырехсторонние пирамиды полезны для конформного соединения шестиугольников с тетрадями. Трехсторонние призмы используются для пограничных слоев, соответствующих тет-сетке дальней части объекта.

Поверхностные сетки полезны в компьютерной графике, где поверхности объектов отражают свет (а также подповерхностное рассеяние ), и полная трехмерная сетка не требуется. Поверхностные сетки также используются для моделирования тонких объектов, таких как листовой металл в автомобилестроении и экстерьеров зданий в архитектуре. Кубические сетки большой размерности (например, 17) широко распространены в астрофизике и теории струн .

Математическое определение и варианты

Каково точное определение сетки ? Не существует общепринятого математического описания, применимого во всех контекстах. Однако некоторые математические объекты явно представляют собой сетки: симплициальный комплекс — это сетка, состоящая из симплексов.Большинство многогранных (например, кубических) сеток являются конформными, то есть имеют ячеистую структуру комплекса CW , обобщения симплициального комплекса . Сетка не обязательно должна быть симплициальной, поскольку произвольное подмножество узлов ячейки не обязательно является ячейкой: например, три узла четырехугольника не определяют ячейку.Однако две ячейки пересекаются в ячейках: например, четырехугольник не имеет узла внутри. Пересечением двух ячеек может быть несколько ячеек: например, два четырехугольника могут иметь два ребра. Пересечение, состоящее из более чем одной ячейки, иногда запрещено и редко желательно; Целью некоторых методов улучшения сетки (например, подушек) является удаление этих конфигураций. В некоторых контекстах проводится различие между топологической сеткой и геометрической сеткой, вложение которой удовлетворяет определенным критериям качества.

Важные варианты сетки, которые не являются комплексами CW, включают неконформные сетки, в которых ячейки не встречаются строго лицом к лицу, но, тем не менее, ячейки разделяют домен. Примером этого является октодерево , где грань элемента может быть разделена гранями соседних элементов. Такие сетки полезны для моделирования потоков. В сетках смещения имеется несколько конформных сеток, которые геометрически перекрываются и не разделяют область; см., например, Overflow, решатель FLOW сетки OVERset . Так называемые бессеточные или бессеточные методы часто используют некоторую дискретизацию области, подобную сетке, и имеют базисные функции с перекрывающейся поддержкой. Иногда рядом с каждой точкой степени свободы моделирования создается локальная сетка, и эти сетки могут перекрываться и быть неконформными друг другу.

Неявные триангуляции основаны на дельта-комплексе: для каждого треугольника указаны длины его ребер и карта склейки между ребрами граней. (пожалуйста, расширьте)

Элементы высокого порядка

Многие сетки используют линейные элементы, где отображение абстрактного элемента на реализованный является линейным, а края сетки представляют собой прямые сегменты.Полиномиальные отображения более высокого порядка распространены, особенно квадратичные. Основная цель элементов более высокого порядка — более точно представить границу области, хотя они также имеют преимущества в точности внутри сетки.Одна из причин использования кубических сеток заключается в том, что линейные кубические элементы имеют те же численные преимущества, что и квадратичные симплициальные элементы.В методе моделирования изогеометрического анализа ячейки сетки, содержащие границу области, используют представление САПР напрямую вместо линейной или полиномиальной аппроксимации.

Улучшение сетки

Улучшение сетки предполагает изменение ее дискретной связности, непрерывного геометрического положения ее ячеек или того и другого. При дискретных изменениях для симплициальных элементов меняют местами ребра и вставляют/удаляют узлы. Те же виды операций выполняются для кубических (квадратных/шестнадцатеричных) сеток, хотя возможных операций меньше, а локальные изменения имеют глобальные последствия. Например, для шестигранной сетки слияние двух узлов создает ячейки, которые не являются шестиугольниками, но если диагонально противоположные узлы четырехугольника объединяются, и это приводит к схлопыванию всего столбца шестигранников, соединенных гранями, тогда все оставшиеся ячейки все равно будут шестигранники. При адаптивном уточнении сетки элементы разбиваются (h-уточнение) в областях, где вычисляемая функция имеет высокий градиент.Сетки также огрубляются, удаляя элементы для повышения эффективности. Многосеточный метод выполняет нечто похожее на уточнение и огрубление, чтобы ускорить численное решение, но без фактического изменения сетки.

При непрерывных изменениях узлы перемещаются или грани более высокой размерности перемещаются путем изменения полиномиального порядка элементов. Перемещение узлов для улучшения качества называется «сглаживанием» или «r-уточнением», а увеличение порядка элементов — «p-уточнением». Узлы также перемещаются в симуляциях, где форма объектов меняется со временем. Это ухудшает форму элементов. Если объект достаточно деформируется, весь объект перерисовывается, а текущее решение сопоставляется со старой сеткой на новую.

Исследовательское сообщество

Практикующие

Эта область является очень междисциплинарной, ее вклад можно найти в математике , информатике и инженерии . Исследования и разработки в области создания сеток отличаются равным вниманием к дискретной и непрерывной математике и вычислениям, как и в случае с вычислительной геометрией , но в отличие от теории графов (дискретный) и численного анализа (непрерывный). Создание сетки обманчиво сложно: людям легко понять, как создать сетку данного объекта, но трудно запрограммировать компьютер так, чтобы он априори принимал правильные решения для произвольных входных данных. В природе и искусственных объектах существует бесконечное разнообразие геометрии. Многие исследователи создания сеток были первыми пользователями сеток. Генерация сетки продолжает получать широкое внимание, поддержку и финансирование, поскольку время, затрачиваемое человеком на создание сетки, затмевает время на настройку и решение расчетов после завершения создания сетки. Такая ситуация всегда была с момента изобретения численного моделирования и компьютерной графики, потому что по мере совершенствования компьютерного оборудования и простого программного обеспечения для решения уравнений люди привлекались к более крупным и сложным геометрическим моделям в стремлении к большей точности, научному пониманию и художественное выражение.

Журналы

Исследования создания сеток публикуются во многих журналах. Это соответствует междисциплинарному характеру исследований, необходимых для достижения прогресса, а также широкому спектру приложений, в которых используются сетки. Ежегодно в 20 журналах появляется около 150 публикаций о сетке, причем в одном журнале появляется не более 20 публикаций. Не существует журнала, основной темой которого было бы создание сеток. Журналы, публикующие не менее 10 статей по сетке в год, выделены жирным шрифтом.

Конференции

(Конференции, основной темой которых является создание сеток, выделены жирным шрифтом. )

Встреча AIAA по аэрокосмическим наукам (15 докладов/документов)
Канадская конференция по вычислительной геометрии CCCG
CompIMAGE: Международный симпозиум по компьютерному моделированию объектов, представленных в изображениях
Конференция AIAA по вычислительной гидродинамике
Конференция по вычислительной гидродинамике ECCOMAS
Вычислительная наука и инженерия CS&E
Конференция по созданию числовых сеток ISGG
Ежегодная конференция Eurographics (Eurographics)] (материалы на форуме компьютерной графики )
Геометрическое и физическое моделирование SIAM
Международная конференция по изогеометрическому анализу IGA
Международный симпозиум по вычислительной геометрии SoCG
Численная геометрия, генерация сеток и научные вычисления (NUMGRID) (материалы в конспектах лекций по вычислительной науке и технике )
Международный круглый стол по сетке SIAM (SIAM IMR) . Независимая ежегодная конференция с 1992 по 2021 год и семинар SIAM, совпадающий с SIAM PP или SIAM CS&E с 2022 года. Рецензируемые протоколы.
SIGGRAPH (труды по транзакциям ACM по графике )
Симпозиум по геометрической обработке SGP ( Eurographics ) (труды на форуме компьютерной графики )
Всемирный конгресс по инженерии

Мастер-классы

Семинары, основной темой которых является создание сетки, выделены жирным шрифтом.

Конференция по геометрии: теория и приложения CGTA
Европейский семинар по вычислительной геометрии EuroCG
Осенний семинар по вычислительной геометрии
Конечные элементы в жидкостях FEF
Симпозиум MeshTrends (в разные годы WCCM или USNCCM)
Методы политопальных элементов в математике и технике
Мастерская Тетраэдра

См. также

Триангуляция Делоне - Метод триангуляции
Алгоритм Фортуны - алгоритм построения диаграммы Вороного
Классификация сетки
Параметризация сетки
Бессеточные методы
Параллельная генерация сетки
Принципы построения сетки
Полигональная сетка
Регулярная сетка
Алгоритм Руперта — алгоритмы создания сетки.
Метод растянутой сетки
Тесселяция (компьютерная графика)
Виды сетки
Неструктурированная сетка

Ссылки

^ Андерсон, Дейл (2012). Вычислительная механика жидкости и теплопередача, третье издание серии «Вычислительные и физические процессы в механике и теплотехнике» . ЦРК Пресс. стр. 679–712. ISBN 978-1591690375 .
^ Уинслоу, А. (1966). «Численное решение квазилинейного уравнения Пуассона». Дж. Компьютер. Физ . 1 (2): 149–172. дои : 10.1016/0021-9991(66)90001-5 .
^ Томпсон, Дж. Ф.; Темза, ФК; Мастин, CW (1974). «Автоматическая численная генерация криволинейной системы координат, соответствующей телу, для поля, содержащего любое количество произвольных двумерных тел». Дж. Компьютер. Физ . 15 (3): 299–319. Бибкод : 1974JCoPh..15..299T . дои : 10.1016/0021-9991(74)90114-4 .
^ Янг, Дэвид (1954). «Итерационные методы решения уравнений в частных производных эллиптического типа» . Труды Американского математического общества . 76 (1): 92–111. дои : 10.2307/1990745 . ISSN 1088-6850 . JSTOR 1990745 .
^ Стегер, Дж.Л.; Соренсон, Р.Л. (1980). «Использование гиперболического уравнения в частных производных для генерации координат тела, методы создания числовых сеток» (PDF) . Публикация конференции НАСА 2166 : 463–478.
^ Венкатакришнан, В; Мавриплис, DJ (май 1991 г.). «Неявные решатели для неструктурированных сеток». Журнал вычислительной физики . 105 (1): 23. doi : 10.1006/jcph.1993.1055 . hdl : 2060/19910014812 . S2CID 123202432 .
^ Уэзерилл, Северная Каролина (сентябрь 1992 г.). «Триангуляция Делоне в вычислительной гидродинамике». Компьютеры и математика с приложениями . 24 (5–6): 129–150. дои : 10.1016/0898-1221(92)90045-j .
^ Андерсон, Д.А.; Шарп Х.Н. (июль 1993 г.). «Генерация ортогональной адаптивной сетки с фиксированными внутренними границами для моделирования нефтяных резервуаров» . Серия SPE «Передовые технологии» . 2. 1 (2): 53–62. дои : 10.2118/21235-PA .

Библиография

Эдельсбруннер, Герберт (2001), «Геометрия и топология для создания сетки», Обзоры прикладной механики , 55 (1), Cambridge University Press: B1–B2, Bibcode : 2002ApMRv..55B...1E , doi : 10.1115/1.1445302 , ISBN 978-0-521-79309-4 .
Фрей, Паскаль Жан; Джордж, Поль-Луи (2000), Создание сетки: применение к конечным элементам , Hermes Science, ISBN 978-1-903398-00-5 .
П. Смит и С. С. Сритаран (1988), «Теория генерации гармонических сеток» (PDF) , Комплексные переменные , 10 (4): 359–369, doi : 10.1080/17476938808814314
С. С. Шритаран (1992), «Теория генерации гармонических сеток-II», Applicable Analysis , 44 (1): 127–149, doi : 10.1080/00036819208840072
Томпсон, Дж. Ф. ; Варси, ЗУА; Мастин, CW (1985), Создание числовых сеток: основы и приложения , Северная Голландия , Elsevier .
CGAL Библиотека алгоритмов вычислительной геометрии
Оден, Дж. Тинсли; Чо, младший (1996), «Адаптивные методы hpq-конечных элементов для иерархических моделей пластинчатых и оболочечных структур», Компьютерные методы в прикладной механике и инженерии , 136 (3): 317–345, Bibcode : 1996CMAME.136. .317O , дои : 10.1016/0045-7825(95)00986-8
Стивен Дж. Оуэн (1998), Обзор технологии создания неструктурированных сеток , Международный круглый стол по сетке, стр. 239–267, S2CID 2675840
Симада, Кенджи; Госсард, Дэвид К. (1995). Пузырьковая сетка: автоматическое создание треугольной сетки немногообразной геометрии с помощью упаковки сфер . Симпозиум ACM по твердотельному моделированию и приложениям, SMA. АКМ. стр. 409-419 . дои : 10.1145/218013.218095 . ISBN 0-89791-672-7 . S2CID 1282987 .

Ян Брандтс, Сергей Коротов, Михал Крижек: «Симплициальные разбиения с приложениями к методу конечных элементов», Монографии Springer по математике, ISBN 978-3030556761 (2020). URL=" https://www.springer.com/gp/book/9783030556761 "
Методы построения сеток - Лисейкин, Владимир Д.

Внешние ссылки

Генераторы сетки

Во многих описаниях коммерческих продуктов особое внимание уделяется моделированию, а не технологии построения сеток, которая позволяет моделировать.

Списки генераторов сетки (внешних):
- Бесплатные генераторы сеток с открытым исходным кодом
- Общественные и коммерческие генераторы сеток
Препроцессор ANSA
АНСИС
CD-adapco и Siemens DISW
Кометные решения
CGAL Библиотека алгоритмов вычислительной геометрии
- Генерация сетки
  - 2D-согласованные триангуляции и сетки
  - 3D Mesh Generation
ЛОКОТЬ
Ennova
Гмш
Гестремальные сетки
МешЛаб
Программное обеспечение MSC
Omega_h Tri/Tet Адаптивность
открытой пенопластовой сетки Создание и преобразование
Саломея Сетчатый модуль
ТетГен
ТетВильд
ТРЕУГОЛЬНИК Генерация сетки и триангуляция Делоне

Многодоменные генераторы разделенных сеток

Эти инструменты создают секционированные сетки, необходимые для моделирования методом конечных элементов из нескольких материалов.

MDM (Multiple Domain Meshing) автоматически и эффективно создает неструктурированные тетраэдральные и шестигранные сетки для составной области, состоящей из гетерогенных материалов.
QMDM (Quality Multi-Domain Meshing) создает высококачественные, взаимно согласованные сетки треугольных поверхностей для нескольких областей.
QMDMNG (качественная многодоменная сетка без зазоров) создает качественные сетки, каждая из которых представляет собой двумерное многообразие и не имеет зазоров между двумя соседними сетками.
SOFA_mesh_partitioning_tools генерирует разделенные тетраэдральные сетки для FEM из нескольких материалов на основе CGAL.

Статьи

Исследовательские группы и люди

Модели и сетки

Полезные модели (входные данные) и сетки (выходные данные) для сравнения алгоритмов построения сетки и сеток.

В HexaLab есть модели и сетки, которые были опубликованы в исследовательских статьях, реконструированы или взяты из оригинальной статьи.
Тест Princeton Shape Benchmark, заархивировано 3 июля 2021 г. на Wayback Machine.
Конкурс по восстановлению формы SHREC каждый год предлагает разные модели, например:
- Конкурс по восстановлению формы нежестких 3D водонепроницаемых сеток 2011
Сетчатые модели Thingi10k из Thingiverse

САПР-модели

Механизмы моделирования, связанные с программным обеспечением для создания сетки, для представления геометрии области.

Форматы файлов сетки

Общие (выходные) форматы файлов для описания сеток.

NetCDF
Бытие/Исход
XDMF
ВТК/ВТУ
МЕДИТИРОВАТЬ
С/Саломея
Гмш
Сетка ANSYS
ВЫКЛЮЧЕННЫЙ
Волновой фронт OBJ
ПЛИ
СТЛ
meshio может конвертировать все вышеперечисленные форматы.

Меш-визуализаторы

Учебники

Учебники по кубиту

[1] Андерсон, Дейл (2012). Вычислительная механика жидкости и теплопередача, третье издание серии «Вычислительные и физические процессы в механике и теплотехнике» . ЦРК Пресс. стр. 679–712. ISBN 978-1591690375 .

[2] Уинслоу, А. (1966). «Численное решение квазилинейного уравнения Пуассона». Дж. Компьютер. Физ . 1 (2): 149–172. дои : 10.1016/0021-9991(66)90001-5 .

[3] Томпсон, Дж. Ф.; Темза, ФК; Мастин, CW (1974). «Автоматическая численная генерация криволинейной системы координат, соответствующей телу, для поля, содержащего любое количество произвольных двумерных тел». Дж. Компьютер. Физ . 15 (3): 299–319. Бибкод : 1974JCoPh..15..299T . дои : 10.1016/0021-9991(74)90114-4 .

[4] Янг, Дэвид (1954). «Итерационные методы решения уравнений в частных производных эллиптического типа» . Труды Американского математического общества . 76 (1): 92–111. дои : 10.2307/1990745 . ISSN 1088-6850 . JSTOR 1990745 .

[5] Стегер, Дж.Л.; Соренсон, Р.Л. (1980). «Использование гиперболического уравнения в частных производных для генерации координат тела, методы создания числовых сеток» (PDF) . Публикация конференции НАСА 2166 : 463–478.

[6] Венкатакришнан, В; Мавриплис, DJ (май 1991 г.). «Неявные решатели для неструктурированных сеток». Журнал вычислительной физики . 105 (1): 23. doi : 10.1006/jcph.1993.1055 . hdl : 2060/19910014812 . S2CID 123202432 .

[7] Уэзерилл, Северная Каролина (сентябрь 1992 г.). «Триангуляция Делоне в вычислительной гидродинамике». Компьютеры и математика с приложениями . 24 (5–6): 129–150. дои : 10.1016/0898-1221(92)90045-j .

[8] Андерсон, Д.А.; Шарп Х.Н. (июль 1993 г.). «Генерация ортогональной адаптивной сетки с фиксированными внутренними границами для моделирования нефтяных резервуаров» . Серия SPE «Передовые технологии» . 2. 1 (2): 53–62. дои : 10.2118/21235-PA .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

v т и Генерация сетки
Types of mesh	Polygon mesh Triangle mesh Volume mesh
Methods	Laplacian smoothing Parallel mesh generation Stretched grid method
Related	Chew's second algorithm Image-based meshing Marching cubes Marching tetrahedra Principles of Grid Generation Regular grid Ruppert's algorithm Tessellation Unstructured grid

Базы данных авторитетного контроля
National	France BnF data Germany Israel United States
Other	IdRef