Шестигранник
Шестигранник ( ( мн.: шестигранники или шестигранники ) или сексаэдр гранями мн.: сексаэдры или сексаэдры ) это любой многогранник с шестью — . Куб , например, представляет собой правильный граней шестигранник со всеми квадратами и тремя квадратами вокруг каждой вершины .
Существует семь топологически различных выпуклых шестигранников. [1] один из которых существует в двух зеркальных формах. Существует три топологически различных вогнутых шестигранника. Два многогранника являются «топологически различными», если они имеют существенно различное расположение граней и вершин, так что невозможно исказить один в другой, просто изменяя длины ребер или углы между ребрами или гранями.
Выпуклый, Кубовидный
[ редактировать ]| Четырехгранный шестигранник ( кубовидный ) 6 граней, 12 ребер, 8 вершин. | ||||||
|---|---|---|---|---|---|---|
 |  |  |  |  | 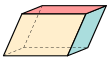 | 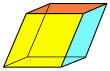 |
| Куб ( квадрат ) | Прямоугольный кубоид (три пары прямоугольники ) | Трехугольный трапецоэдр ( ромбы совпадают ) | Трехугольный трапецоэдр (равные четырехугольники ) | Четырехсторонняя деталь (обрезанный по вершине квадратная пирамида ) | Параллелепипед (три пары параллелограммы ) | Ромбоэдр (три пары Ромб ) |
| О ч , [4,3], (*432) заказать 48 | Д 2h , [2,2], (*222) заказать 8 | Д 3 д , [2 + ,6], (2*3) заказать 12 | Д 3 , [2,3] + , (223) заказать 6 | С 4в , [4], (*44) заказать 8 | С я , [2 + ,2 + ], (×) заказ 2 | |
Выпуклые, Другие
[ редактировать ]| Выпуклый | |||||
|---|---|---|---|---|---|
 |   |  |  |  | 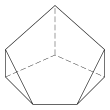 |
| Треугольная бипирамида | Четырехугольный антиклин. Хиральный - существует в «левосторонней» и «правосторонней» зеркальной форме. | Пятиугольная пирамида | |||
| 3 6 Лица 9Е, 5В | 4.4.3.3.3.3 Лица 10Е, 6В | 4.4.4.4.3.3 Лица 11 Е, 7 В | 5.3 5 Лица 10Е, 6В | 5.4.4.3.3.3 Лица 11 Е, 7 В | 5.5.4.4.3.3 Лица 12Е, 8В |
Вогнутый
[ редактировать ]Есть еще три топологически различных шестигранника, которые можно реализовать только как вогнутые фигуры:
| Вогнутый | ||
|---|---|---|
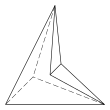 | 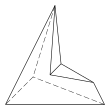 | 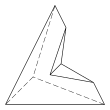 |
| 4.4.3.3.3.3 Лица 10Е, 6В | 5.5.3.3.3.3 Лица 11 Е, 7 В | 6.6.3.3.3.3 Лица 12Е, 8В |
Двуугольную можно рассматривать как антипризму вырожденную форму шестигранника, имеющую две противоположные двуугольные грани и четыре треугольные грани. Однако двуугольники обычно не учитываются при определении несферических многогранников, и этот случай часто рассматривают просто как тетраэдр, а четыре оставшиеся треугольные грани считаются составляющими полное тело.
См. также
[ редактировать ]Ссылки
[ редактировать ]Внешние ссылки
[ редактировать ]- Многогранники с 4-7 гранями , Стивен Датч