Гиперграф

Пример неориентированного гиперграфа с $X=\{v_{1},v_{2},v_{3},v_{4},v_{5},v_{6},v_{7}\}$ и $E=\{e_{1},e_{2},e_{3},e_{4}\}=$ $\{\{v_{1},v_{2},v_{3}\},$ $\{v_{2},v_{3}\},$ $\{v_{3},v_{5},v_{6}\},$ $\{v_{4}\}\}$. Этот гиперграф имеет порядок 7 и размер 4. Здесь ребра соединяют не две вершины, а несколько и представлены цветами.

Альтернативное представление гиперграфа, представленного на рисунке выше, называется PAOH. Ребра — это вертикальные линии, соединяющие вершины. V7 — изолированная вершина. Вершины выравниваются по левому краю. В легенде справа показаны названия ребер.

Пример направленного гиперграфа с $X=\{1,2,3,4,5,6\}$ и $E=\{a_{1},a_{2},a_{3},a_{4},a_{5}\}=$ $\{(\{1\},\{2\}),$ $(\{2\},\{3\}),$ $(\{3\},\{1\}),$ $(\{2,3\},\{4,5\}),$ $(\{3,5\},\{6\})\}$.

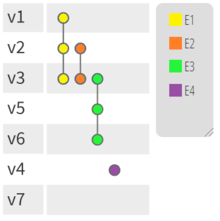
В математике гиперграф — это обобщение графа , в котором ребро может соединять любое количество вершин . Напротив, в обычном графе ребро соединяет ровно две вершины.

Формально ориентированный гиперграф — это пара $(X,E)$, где $X$ представляет собой набор элементов, называемых узлами , вершинами , точками или элементами , и $E$ представляет собой набор пар подмножеств $X$. Каждая из этих пар $(D,C)\in E$ называется ребром или гиперребром ; подмножество вершин $D$ известен как его хвост или домен , и $C$ в качестве его головы или кодомена .

Порядок гиперграфа $(X,E)$ это количество вершин в $X$. Размер гиперграфа — это количество ребер в $E$. Порядок ребра $e=(D,C)$ в ориентированном гиперграфе $|e|=(|D|,|C|)$: то есть количество вершин в его хвосте, за которым следует количество вершин в его голове.

Приведенное выше определение обобщает ориентированный граф на ориентированный гиперграф, определяя начало или хвост каждого ребра как набор вершин ( $C\subseteq X$ или $D\subseteq X$), а не как одну вершину. Граф является частным случаем, когда каждое из этих множеств содержит только один элемент. Следовательно, любая стандартная концепция теории графов, независимая от порядков ребер, $|e|$ обобщим на теорию гиперграфов.

Согласно одному определению, неориентированный гиперграф $(X,E)$ является ориентированным гиперграфом, имеющим симметричное множество ребер: если $(D,C)\in E$ затем $(C,D)\in E$. Для простоты обозначений можно удалить «дубликаты» гиперребра, поскольку модификатор «ненаправленный» точно информирует нас о их существовании: Если $(D,C)\in E$ затем $(C,D){\vec {\in }}E$ где ${\vec {\in }}$ означает неявно в .

В то время как ребра графа соединяют только 2 узла, гиперребра соединяют произвольное количество узлов. Однако часто желательно изучать гиперграфы, в которых все гиперребра имеют одинаковую мощность; k -однородный гиперграф — это гиперграф, все его гиперребра имеют размер k . (Другими словами, один такой гиперграф представляет собой набор множеств, каждый такой набор представляет собой гиперребро, соединяющее k узлов.) Таким образом, 2-однородный гиперграф — это граф, 3-однородный гиперграф — это набор неупорядоченных троек и так далее. Неориентированный гиперграф также называют системой множеств или семейством множеств, взятых из универсального множества .

Гиперграфы можно рассматривать как структуры инцидентности . двудольный «граф инцидентности» или « граф Леви В частности, каждому гиперграфу соответствует », и наоборот, каждый двудольный граф можно рассматривать как граф инцидентности гиперграфа, когда он двухцветный и указано, какой класс цвета соответствует вершинам гиперграфа, а который — ребрам гиперграфа.

Гиперграфы имеют много других названий. В вычислительной геометрии неориентированный гиперграф иногда можно назвать пространством диапазонов , а гиперребра — диапазонами . В теории кооперативных игр гиперграфы называются простыми играми (играми с голосованием); это понятие применяется для решения проблем теории социального выбора . В некоторой литературе края называются гиперссылками или соединителями .

Совокупность гиперграфов — это категория гиперграфов гомоморфизмы которой являются , морфизмами .

Приложения

Неориентированные гиперграфы полезны при моделировании таких вещей, как проблемы выполнимости, базы данных, машинное обучение, и проблемы дерева Штейнера . Они широко использовались в задачах машинного обучения в качестве модели данных и регуляризации классификаторов (математика) . Приложения включают в себя рекомендательную систему (сообщества в виде гиперребер), поиск изображений (корреляции в виде гиперребер), и биоинформатика (биохимические взаимодействия как гиперребра). Типичные методы обучения гиперграфов включают спектральную кластеризацию гиперграфов , которая расширяет теорию спектральных графов с помощью лапласиана гиперграфа, и обучение с полуконтролем гиперграфа , которое вносит дополнительные структурные затраты на гиперграф, чтобы ограничить результаты обучения. Для крупномасштабных гиперграфов используется распределенная структура. созданный с использованием Apache Spark также доступен .

Направленные гиперграфы можно использовать для моделирования таких вещей, как телефонные приложения, выявление отмывания денег , исследование операций, и планирование перевозок. Их также можно использовать для моделирования выполнимости по Хорну .

Обобщения понятий из графов

Многие теоремы и концепции, связанные с графами, справедливы и для гиперграфов, в частности:

• Сопоставление в гиперграфах ;
• Вершинное покрытие в гиперграфах (также известное как трансверсальное );
• Линейный график гиперграфа ;
• Грамматика гиперграфа — создается путем дополнения класса гиперграфов набором правил замены;
• теорема Рамсея ;
• теорема Эрдеша–Ко–Радо ;
• теорема Краскала–Катона о равномерных гиперграфах;
• Теоремы типа Холла для гиперграфов .

В ориентированных гиперграфах: транзитивное замыкание и задачи о кратчайшем пути.

Гиперграфический рисунок

Эту принципиальную схему можно интерпретировать как рисунок гиперграфа, в котором четыре вершины (изображенные в виде белых прямоугольников и дисков) соединены тремя гиперребрами, нарисованными в виде деревьев.

Хотя гиперграфы рисовать на бумаге труднее, чем графики, несколько исследователей изучали методы визуализации гиперграфов.

В одном из возможных визуальных представлений гиперграфов, аналогичном стандартному стилю рисования графов , в котором кривые на плоскости используются для изображения ребер графа, вершины гиперграфа изображаются в виде точек, дисков или прямоугольников, а его гиперребра изображаются в виде деревьев, имеющих вершины как их листья. Если вершины представлены в виде точек, гиперребра также могут быть показаны в виде гладких кривых, соединяющих наборы точек, или в виде простых замкнутых кривых , охватывающих наборы точек.

Диаграмма Венна 4-го порядка, которую можно интерпретировать как изображение подразделения гиперграфа с 15 вершинами (15 цветными областями) и 4 гиперребрами (4 эллипсами).

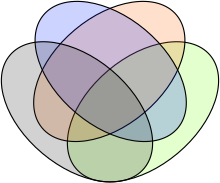
В другом стиле визуализации гиперграфа, модели подразделения рисунка гиперграфа, плоскость подразделяется на области, каждая из которых представляет одну вершину гиперграфа. Гиперребра гиперграфа представлены смежными подмножествами этих областей, которые можно обозначить раскраской, рисованием контуров вокруг них или и тем, и другим. порядка n Например, диаграмму Венна можно рассматривать как изображение подразделения гиперграфа с n гиперребрами (кривыми, определяющими диаграмму) и 2 ^н − 1 вершина (представленная областями, на которые эти кривые делят плоскость). за полиномиальное время В отличие от распознавания плоских графов , NP-полно определить, имеет ли гиперграф планарное подразделение. но существование рисунка этого типа можно эффективно проверить, если шаблон смежности областей ограничен путем, циклом или деревом.

Альтернативное представление гиперграфа под названием PAOH. показано на рисунке вверху этой статьи. Ребра — это вертикальные линии, соединяющие вершины. Вершины выровнены по левому краю. В легенде справа показаны названия ребер. Он был разработан для динамических гиперграфов, но может использоваться и для простых гиперграфов.

Раскраска гиперграфа

Классическая раскраска гиперграфа заключается в присвоении одного из цветов из набора. $\{1,2,3,...,\lambda \}$ к каждой вершине гиперграфа так, чтобы каждое гиперребро содержало хотя бы две вершины разных цветов. Другими словами, не должно быть одноцветного гиперребра с мощностью не ниже 2. В этом смысле это прямое обобщение раскраски графа. Минимальное количество используемых различных цветов во всех раскрасках называется хроматическим числом гиперграфа.

Гиперграфы, для которых существует раскраска с использованием до k цветов, называются k-раскрашиваемыми . Гиперграфы, раскрашиваемые в 2 цвета, в точности являются двудольными.

Существует множество обобщений классической раскраски гиперграфов. Один из них — это так называемая смешанная раскраска гиперграфа, когда допускаются одноцветные ребра. Некоторые смешанные гиперграфы невозможно раскрасить в любое количество цветов. Общий критерий бесцветности неизвестен. Если смешанный гиперграф раскрашивается, то минимальное и максимальное количество используемых цветов называются нижним и верхним хроматическими числами соответственно.

Свойства гиперграфов

Гиперграф может иметь различные свойства, такие как:

• Пустой – не имеет краев.
• Непростой (или множественный ) — имеет петли (гиперребра с одной вершиной) или повторяющиеся ребра, что означает, что может быть два или более ребер, содержащих один и тот же набор вершин.
• Простой – не имеет петель и повторяющихся краев.
• $d$-regular - каждая вершина имеет степень $d$, т. е. содержится ровно в $d$ гиперребра.
• 2-раскрашиваемый - его вершины можно разбить на два класса U и V так, что каждое гиперребро мощности не менее 2 содержит хотя бы по одной вершине из обоих классов. Альтернативный термин — Свойство B.
  • Два более сильных свойства — двудольное и сбалансированное .
• $k$-однородный – каждое гиперребро содержит ровно $k$ вершины.
• $k$-partite – вершины разбиты на $k$ частей, и каждое гиперребро содержит ровно по одной вершине каждого типа.
  • Каждый $k$-частичный гиперграф (для $k\geq 2$) оба $k$-однородные и двудольные (и 2-цветные).
• Уменьшенный : ни одно гиперребро не является строгим подмножеством другого гиперребра; эквивалентно, каждое гиперребро максимально для включения. Редукция . гиперграфа — это уменьшенный гиперграф, полученный удалением каждого гиперребра, входящего в другое гиперребро
• Замкнутость вниз - каждое подмножество ребер неориентированного гиперграфа также является гиперребром. Замкнутый вниз гиперграф обычно называют абстрактным симплициальным комплексом . Обычно оно не сокращается, если только все гиперребра не имеют мощности 1.
  • Абстрактный симплициальный комплекс, обладающий свойством приращения, называется матроидом .
• Ламинарный : для любых двух гиперребер либо они не пересекаются, либо одно входит в другое. Другими словами, множество гиперребер образует семейство ламинарных множеств .

Связанные гиперграфы

Поскольку ссылки гиперграфа могут иметь любую мощность, существует несколько понятий понятия подграфа, называемых подгиперграфами , частичными гиперграфами и гиперграфами секций .

Позволять $H=(X,E)$ — гиперграф, состоящий из вершин

$X=\lbrace x_{i}\mid i\in I_{v}\rbrace ,$

и имеющий набор кромок

$E=\lbrace e_{i}\mid i\in I_{e},e_{i}\subseteq X,e_{i}\neq \emptyset \rbrace ,$

где $I_{v}$ и $I_{e}$ являются наборами индексов вершин и ребер соответственно.

Подгиперграф . — это гиперграф, из которого удалены некоторые вершины Формально подгиперграф $H_{A}$ вызванный $A\subseteq X$ определяется как

$H_{A}=\left(A,\lbrace e\cap A\mid e\in E,e\cap A\neq \emptyset \rbrace \right).$

Альтернативный термин ограничение H на A. —

Расширение подгиперграфа — это гиперграф, в котором каждое гиперребро $H$ который частично содержится в подгиперграфе $H_{A}$ полностью содержится в расширении $Ex(H_{A})$. Формально

$Ex(H_{A})=(A\cup A',E')$ с $A'=\bigcup _{e\in E}e\setminus A$ и $E'=\lbrace e\in E\mid e\subseteq (A\cup A')\rbrace$.

— Частичный гиперграф это гиперграф, у которого удалены некоторые ребра. Учитывая подмножество $J\subset I_{e}$ набора индексов ребер, частичный гиперграф, созданный $J$ это гиперграф

$\left(X,\lbrace e_{i}\mid i\in J\rbrace \right).$

Учитывая подмножество $A\subseteq X$, гиперграф сечения является частичным гиперграфом

$H\times A=\left(A,\lbrace e_{i}\mid i\in I_{e},e_{i}\subseteq A\rbrace \right).$

Двойной ​ $H^{*}$ из $H$ — это гиперграф, вершины и ребра которого поменяны местами, так что вершины имеют вид $\lbrace e_{i}\rbrace$ и чьи ребра заданы выражением $\lbrace X_{m}\rbrace$ где

$X_{m}=\lbrace e_{i}\mid x_{m}\in e_{i}\rbrace .$

Когда понятие равенства правильно определено, как это сделано ниже, операция взятия двойственного гиперграфа является инволюцией , т. е.

$\left(H^{*}\right)^{*}=H.$

G Связный граф с тем же набором вершин, что и связный гиперграф H, является главным графом для H, если каждое гиперребро H индуцирует связный подграф в G . Для несвязного гиперграфа H является хост-графом , G если существует взаимно однозначное соответствие между связными компонентами G G и H , так что каждый связный компонент ' из G является хостом соответствующего H' .

граф 2-секционный (или граф клик , представляющий граф , простой граф , граф Гейфмана ) гиперграфа — это граф с одинаковыми вершинами гиперграфа и ребрами между всеми парами вершин, содержащимися в одном и том же гиперребре.

Матрица заболеваемости

Позволять $V=\{v_{1},v_{2},~\ldots ,~v_{n}\}$ и $E=\{e_{1},e_{2},~\ldots ~e_{m}\}$. Каждый гиперграф имеет $n\times m$ матрица заболеваемости .

Для неориентированного гиперграфа $I=(b_{ij})$ где

$b_{ij}=\left\{{\begin{matrix}1&\mathrm {if} ~v_{i}\in e_{j}\\0&\mathrm {otherwise} .\end{matrix}}\right.$

Транспонирование ​ $I^{t}$ определяет матрицы инцидентности гиперграф $H^{*}=(V^{*},\ E^{*})$ называется двойственным ​ $H$, где $V^{*}$ представляет собой набор m -элементов и $E^{*}$ представляет собой n -элементный набор подмножеств $V^{*}$. Для $v_{j}^{*}\in V^{*}$ и $e_{i}^{*}\in E^{*},~v_{j}^{*}\in e_{i}^{*}$ тогда и только тогда, когда $b_{ij}=1$.

Для направленного гиперграфа головы и хвосты каждого гиперребра $e_{j}$ обозначаются $H(e_{j})$ и $T(e_{j})$ соответственно. $I=(b_{ij})$ где

$b_{ij}=\left\{{\begin{matrix}-1&\mathrm {if} ~v_{i}\in T(e_{j})\\1&\mathrm {if} ~v_{i}\in H(e_{j})\\0&\mathrm {otherwise} .\end{matrix}}\right.$

График заболеваемости

Гиперграф H e1 ) соединены с ребром тогда и только тогда , когда _{может быть представлен двудольным графом BG следующим образом: множества X и E являются частями BG, а (x1} вершина x1 _, содержится ребре _в e . ₁ в Х. ​

И наоборот, любой двудольный граф с фиксированными частями и без несвязных узлов во второй части представляет собой некоторый гиперграф описанным выше способом. Этот двудольный граф также называется графом инцидентности .

Матрица смежности

Параллель для матрицы смежности гиперграфа можно провести из матрицы смежности графа. В случае графа матрица смежности представляет собой квадратную матрицу, которая указывает, являются ли пары вершин смежными . Аналогично мы можем определить матрицу смежности $A=(a_{ij})$ для гиперграфа вообще, где гиперребра $e_{k\leq m}$иметь реальный вес $w_{e_{k}}\in \mathbb {R}$ с

$a_{ij}=\left\{{\begin{matrix}w_{e_{k}}&\mathrm {if} ~(v_{i},v_{j})\in E\\0&\mathrm {otherwise} .\end{matrix}}\right.$

Циклы

В отличие от обычных неориентированных графов, для которых существует одно естественное понятие циклов и ациклических графов , существует множество естественных неэквивалентных определений ацикличности для гиперграфов, которые схлопываются до ацикличности обычного графа для частного случая обычных графов.

Первое определение ацикличности гиперграфов было дано Клодом Берже : Гиперграф является ацикличным по Бержу, если его граф инцидентности ( двудольный граф, определенный выше) ацикличен. Это определение очень ограничительно: например, если в гиперграфе есть некоторая пара $v\neq v'$ вершин и некоторой пары $f\neq f'$ гиперребер таких, что $v,v'\in f$ и $v,v'\in f'$, то оно циклично по Бержу. Цикличность Бержа, очевидно, можно проверить в линейном времени путем исследования графа инцидентности.

Мы можем определить более слабое понятие ацикличности гиперграфа: позже названный α-ацикличностью. Это понятие ацикличности эквивалентно тому, что гиперграф конформен (каждая клика первичного графа покрыта некоторым гиперребром), а его первичный граф является хордальным ; это также эквивалентно сводимости к пустому графу с помощью алгоритма GYO (также известный как алгоритм Грэма), сливающийся итерационный процесс, который удаляет гиперребра, используя обобщенное определение ушей . В области теории баз данных известно, что схема базы данных обладает определенными желательными свойствами, если ее базовый гиперграф является α-ациклическим. Кроме того, α-ацикличность связана и с выразительностью охраняемого фрагмента логики первого порядка .

Мы можем за линейное время проверить , является ли гиперграф α-ациклическим.

Обратите внимание, что α-ацикличность обладает нелогичным свойством: добавление гиперребер к α-циклическому гиперграфу может сделать его α-ациклическим (например, добавление гиперребра, содержащего все вершины гиперграфа, всегда сделает его α-ациклическим). Частично мотивированный этим очевидным недостатком, Рональд Фейгин определили более сильные понятия β-ацикличности и γ-ацикличности. Мы можем сформулировать β-ацикличность как требование, чтобы все подгиперграфы гиперграфа были α-ациклическими, что эквивалентно к более раннему определению Грэма. Понятие γ-ацикличности является более ограничительным условием, которое эквивалентно нескольким желательным свойствам схем баз данных и связано с диаграммами Бахмана . И β-ацикличность, и γ-ацикличность можно проверить за полиномиальное время .

Эти четыре понятия ацикличности сопоставимы: ацикличность по Бержу подразумевает γ-ацикличность, из которой следует β-ацикличность, из которой следует α-ацикличность. Однако ни один из обратных выводов не справедлив, поэтому эти четыре понятия различны.

Изоморфизм, симметрия и равенство

гиперграфа Гомоморфизм — это отображение множества вершин одного гиперграфа в другой, при котором каждое ребро отображается в одно другое ребро.

Гиперграф $H=(X,E)$ изоморфен ​ гиперграфу $G=(Y,F)$, записанный как $H\simeq G$ если существует биекция

$\phi :X\to Y$

и перестановка $\pi$ из $I$ такой, что

$\phi (e_{i})=f_{\pi (i)}$

Биекция $\phi$ тогда называется изоморфизмом графов. Обратите внимание, что

$H\simeq G$ тогда и только тогда, когда $H^{*}\simeq G^{*}$.

Когда ребра гиперграфа явно помечены, возникает дополнительное понятие сильного изоморфизма . Один говорит, что $H$ изоморфен сильно ​ $G$ если перестановка тождественна. Затем один пишет $H\cong G$. Обратите внимание, что все сильно изоморфные графы изоморфны, но не наоборот.

Когда вершины гиперграфа явно помечены, возникают понятия эквивалентности , а также равенства . Один говорит, что $H$ эквивалентно ​ ​ $G$, и пишет $H\equiv G$ если изоморфизм $\phi$ имеет

$\phi (x_{n})=y_{n}$

и

$\phi (e_{i})=f_{\pi (i)}$

Обратите внимание, что

$H\equiv G$ тогда и только тогда, когда $H^{*}\cong G^{*}$

Если, кроме того, перестановка $\pi$ это идентичность, говорят, что $H$ равно $G$, и пишет $H=G$. Обратите внимание, что при таком определении равенства графы самодвойственны:

$\left(H^{*}\right)^{*}=H$

гиперграфа Автоморфизм — это изоморфизм множества вершин в себя, то есть перемаркировка вершин. Множество автоморфизмов гиперграфа H (= ( X , E )) представляет собой группу в композиции, называемую группой автоморфизмов гиперграфа и записываемую Aut( H ).

Примеры

Рассмотрим гиперграф $H$ с краями

$H=\lbrace e_{1}=\lbrace a,b\rbrace ,e_{2}=\lbrace b,c\rbrace ,e_{3}=\lbrace c,d\rbrace ,e_{4}=\lbrace d,a\rbrace ,e_{5}=\lbrace b,d\rbrace ,e_{6}=\lbrace a,c\rbrace \rbrace$

и

$G=\lbrace f_{1}=\lbrace \alpha ,\beta \rbrace ,f_{2}=\lbrace \beta ,\gamma \rbrace ,f_{3}=\lbrace \gamma ,\delta \rbrace ,f_{4}=\lbrace \delta ,\alpha \rbrace ,f_{5}=\lbrace \alpha ,\gamma \rbrace ,f_{6}=\lbrace \beta ,\delta \rbrace \rbrace$

Тогда ясно $H$ и $G$ изоморфны (с $\phi (a)=\alpha$и т. д. ), но они не сильно изоморфны. Так, например, в $H$, вершина $a$ пересекает ребра 1, 4 и 6, так что

$e_{1}\cap e_{4}\cap e_{6}=\lbrace a\rbrace$

На графике $G$, не существует вершины, пересекающей ребра 1, 4 и 6:

$f_{1}\cap f_{4}\cap f_{6}=\varnothing$

В этом примере $H$ и $G$ эквивалентны, $H\equiv G$, а двойственные числа сильно изоморфны: $H^{*}\cong G^{*}$.

Симметрия

The классифицировать $r(H)$ гиперграфа $H$ — максимальная мощность любого из ребер гиперграфа. Если все ребра имеют одинаковую мощность k , гиперграф называется равномерным или k-равномерным или называется k-гиперграфом . Граф — это всего лишь 2-однородный гиперграф.

Степень d(v) вершины v — это количество ребер, содержащих ее. H является k-регулярным, если каждая вершина имеет степень k .

Двойственный однородному гиперграфу является регулярным, и наоборот.

Две вершины x и y графа H называются симметричными , если существует автоморфизм такой, что $\phi (x)=y$. Два края $e_{i}$ и $e_{j}$ называются симметричными, если существует автоморфизм такой, что $\phi (e_{i})=e_{j}$.

Гиперграф называется вершинно-транзитивным (или вершинно-симметричным ), если все его вершины симметричны. Аналогично, гиперграф является транзитивным по ребрам , если все ребра симметричны. Если гиперграф симметричен как по ребрам, так и по вершинам, то гиперграф просто транзитивен .

Из-за двойственности гиперграфа изучение транзитивности ребер идентично изучению транзитивности вершин.

Перегородки

Теорема о разделе Э. Даубера. утверждает, что для реберно-транзитивного гиперграфа $H=(X,E)$, существует раздел

$(X_{1},X_{2},\cdots ,X_{K})$

множества вершин $X$ такой, что подгиперграф $H_{X_{k}}$ созданный $X_{k}$ транзитивно для каждого $1\leq k\leq K$, и такой, что

$\sum _{k=1}^{K}r\left(H_{X_{k}}\right)=r(H)$

где $r(H)$ ранг H. это

Как следствие, реберно-транзитивный гиперграф, который не является вершинно-транзитивным, является двухцветным.

Разделение графов (и, в частности, разделение гиперграфов) имеет множество применений при проектировании ИС. и параллельные вычисления . Эффективные и масштабируемые алгоритмы разделения гиперграфов также важны для обработки крупномасштабных гиперграфов в задачах машинного обучения.

Дальнейшие обобщения

Одно из возможных обобщений гиперграфа — позволить ребрам указывать на другие ребра. Есть два варианта этого обобщения. В одном ребра состоят не только из набора вершин, но могут также содержать подмножества вершин, подмножества подмножеств вершин и так далее до бесконечности . По сути, каждое ребро — это просто внутренний узел дерева или ориентированного ациклического графа , а вершины — это конечные узлы. В таком случае гиперграф представляет собой просто набор деревьев с общими узлами (то есть данный внутренний узел или лист может встречаться в нескольких разных деревьях). И наоборот, любую совокупность деревьев можно понимать как обобщенный гиперграф. Поскольку деревья широко используются в информатике и многих других областях математики, можно сказать, что гиперграфы также появляются естественным образом. Так, например, это обобщение естественным образом возникает как модель алгебры термов ; ребра соответствуют термам , а вершины соответствуют константам или переменным.

Для такого гиперграфа членство во множестве обеспечивает упорядочение, но это упорядочение не является ни частичным порядком , ни предварительным порядком , поскольку оно не является транзитивным. Граф, соответствующий графу Леви этого обобщения, является ориентированным ациклическим графом . Рассмотрим, например, обобщенный гиперграф, множество вершин которого равно $V=\{a,b\}$ и чьи ребра $e_{1}=\{a,b\}$ и $e_{2}=\{a,e_{1}\}$. Тогда, хотя $b\in e_{1}$ и $e_{1}\in e_{2}$, это неправда $b\in e_{2}$. Однако транзитивное замыкание членства в множестве для таких гиперграфов действительно вызывает частичный порядок и «сглаживает» гиперграф в частично упорядоченное множество .

Альтернативно, ребрам может быть разрешено указывать на другие ребра, независимо от требования, чтобы ребра были упорядочены как ориентированные ациклические графы. Это позволяет создавать графы с петлями ребер, которые вообще не обязательно должны содержать вершины. Например, рассмотрим обобщенный гиперграф, состоящий из двух ребер $e_{1}$ и $e_{2}$, и ноль вершин, так что $e_{1}=\{e_{2}\}$ и $e_{2}=\{e_{1}\}$. Поскольку этот цикл бесконечно рекурсивен, множества, являющиеся ребрами, нарушают аксиому Foundation . В частности, для таких гиперграфов не существует транзитивного замыкания принадлежности множеству. Хотя на первый взгляд такие структуры могут показаться странными, их можно легко понять, заметив, что эквивалентное обобщение их графа Леви больше не является двудольным , а представляет собой просто некоторый общий ориентированный граф .

Обобщенная матрица инцидентности для таких гиперграфов по определению является квадратной матрицей ранга, равного общему количеству вершин плюс ребер. Таким образом, для приведенного выше примера матрица инцидентности просто

$\left[{\begin{matrix}0&1\\1&0\end{matrix}}\right].$

См. также

• BF-граф – Тип направленного гиперграфа
• Комбинаторный дизайн - симметричное расположение конечных множеств.
• Факторный граф . Факторный граф — это двудольный граф, представляющий факторизацию функции. Страницы, отображающие описания викиданных в качестве запасного варианта
• Greedoid — система наборов, используемая при жадной оптимизации.
• Структура инцидентности - Абстрактная математическая система двух типов объектов и связи между ними.
• Мультиграф - граф с кратными ребрами между двумя вершинами.
• Система P – Вычислительная модель
• Умножение разреженной матрицы на вектор – процедура вычислений
• Petri Net — модель для описания распределенных систем. Страницы с краткими описаниями целей перенаправления.

Ссылки

• Берже, Клод (1984). Гиперграфы: комбинаторика конечных множеств . Эльзевир. ISBN  978-0-08-088023-5 .
• Берге, К.; Рэй-Чаудхури, Д. (2006). Семинар по гиперграфам: Университет штата Огайо, 1972 г. Конспект лекций по математике. Том. 411. Спрингер. ISBN  978-3-540-37803-7 .
• «Гиперграф» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Бретто, Ален (2013). Теория гиперграфов: Введение . Спрингер. ISBN  978-3-319-00080-0 .
• Волошин, Виталий Иванович (2002). Раскраска смешанных гиперграфов: теория, алгоритмы и приложения: теория, алгоритмы и приложения . Монографии Филдсовского института. Том. 17. Американское математическое общество. ISBN  978-0-8218-2812-0 .
• Волошин, Виталий И. (2009). Введение в теорию графов и гиперграфов . Нова Наука. ISBN  978-1-61470-112-5 .
• В эту статью включены материалы из гиперграфа с сайта PlanetMath , который доступен по лицензии Creative Commons Attribution/Share-Alike License .

Внешние ссылки

• PAOHVis : система PAOHVis с открытым исходным кодом для визуализации динамических гиперграфов.