Матрица мультипризнаков-мультиметодов

Матрица мультипризнаков-мультиметодов ( MTMM ) представляет собой подход к проверке валидности конструкции, разработанный Кэмпбеллом и Фиске (1959). Он организует конвергентные и дискриминантные доказательства достоверности для сравнения того, как мера соотносится с другими мерами. Концептуальный подход повлиял на планирование экспериментов и теорию измерений в психологии, включая приложения в моделях структурных уравнений.

Определения и ключевые компоненты

несколько признаков В этом подходе используются для изучения (а) сходных или (б) несходных признаков ( конструктов ) с целью установления конвергентной и дискриминантной достоверности между признаками. Аналогичным образом, несколько методов в этом подходе используется для изучения дифференциальных эффектов (или их отсутствия), вызванных дисперсией конкретного метода. Результаты могут быть коррелированы, потому что они измеряют схожие характеристики, или потому, что они основаны на схожих методах, или и то, и другое. Когда переменные, которые должны измерять разные конструкции, демонстрируют высокую корреляцию, поскольку они основаны на схожих методах, это иногда описывается как проблема «неприятной дисперсии» или «систематической ошибки метода».

При проверке достоверности конструкции с помощью матрицы MTMM необходимо учитывать шесть основных факторов:

1. Оценка конвергентной валидности . Тесты, предназначенные для измерения одной и той же конструкции, должны сильно коррелировать между собой.
2. Оценка дискриминантной (дивергентной) достоверности . Конструкт, измеряемый с помощью теста, не должен сильно коррелировать с различными конструктами.
3. Единица признака-метода . Каждое задание или тест, используемые при измерении конструкции, считается единицей признака-метода; в том, что дисперсия, содержащаяся в показателе, является частично признаком, а частично методом. Как правило, исследователи стремятся к низкой дисперсии, специфичной для метода, и высокой дисперсии признаков.
4. Мультипризнак-мультиметод . Для установления (а) дискриминантной достоверности и (б) относительного вклада признака или специфичной для метода дисперсии необходимо использовать более одного признака и более одного метода. Этот принцип согласуется с идеями, предложенными Платтом в концепции сильного вывода (1964).
5. Действительно другая методология . При использовании нескольких методов необходимо учитывать, насколько различаются фактические показатели. Например, предоставление двух показателей самоотчета не является на самом деле разными показателями; тогда как можно было бы использовать шкалу интервью или психосоматическое чтение.
6. Характеристики черт . Черты должны быть достаточно разными, чтобы быть различимыми, но достаточно похожими, чтобы их можно было изучить в MTMM.

Пример

В приведенном ниже примере представлена ​​прототипная матрица и показано, что означают корреляции между показателями. Диагональная линия обычно заполняется коэффициентом надежности меры (например, коэффициентом альфа). Описания в скобках [] указывают на то, что ожидается, когда достоверность конструкции (например, депрессия или тревога) и достоверность показателей высоки.

Тест	Опросник депрессии Бека (BDI) – Анкета	Шкала оценки депрессии Гамильтона (HDRS) - Интервью	Опросник тревожности Бека (BAI) – Анкета	Глобальные впечатления клинициста – Тревога (CGI-A) – Интервью
БДИ	(Коэффициент надежности) [около 1,00]
HDRS	Гетерометод-моноприход [самый высокий из всех, кроме надежности]	(Коэффициент надежности) [около 1,00]
ДА	Монометод-гетеропризнак [низкий, меньше монотипа]	Гетерометод-гетерочерта [самый низкий из всех]	(Коэффициент надежности) [близко к 1,00]
CGI-А	Гетерометод-гетерочерта [самый низкий из всех]	Монометод-гетеропризнак [низкий, меньше монотипа]	Гетерометод-моноприход [самый высокий из всех, кроме надежности]	(Коэффициент надежности) [около 1,00]

В этом примере в первой строке перечислены оцениваемые черты характера (т. е. депрессия или тревога), а также метод оценки этой черты (т. е. опросник с самооценкой в ​​сравнении с интервью). Термин «гетерометод» указывает на то, что эта ячейка сообщает о корреляции между двумя отдельными методами. Монометод указывает на то, что вместо этого используется тот же метод (например, интервью и интервью). Гетеропризнак указывает на то, что клетка относится к двум предположительно разным признакам. Моночерта указывает на ту же черту, которую предполагается измерить.

Эта концепция ясно дает понять, что существует по крайней мере два источника дисперсии, которые могут повлиять на наблюдаемые оценки показателя: не только основной признак (который обычно является целью сбора данных в первую очередь), но и метод, используемый для собрать размеры. Матрица MTMM использует два или более показателей каждого признака и два или более метода, чтобы начать различать вклад различных факторов. Первый кадр анимированного рисунка показывает, как четыре измерения в таблице объединены в пары с точки зрения сосредоточения внимания на «чертах» депрессии (BDI и HDRS) и тревоги (BAI и CGI-A). Второй показывает, что они также парны с точки зрения исходного метода: два используют анкеты для самоотчета (часто называемые «опросами»), а два основаны на интервью (которое может включать в себя прямое наблюдение за невербальным общением и поведением, а также как ответ собеседника).

На баллы по каждому показателю влияют как характеристика, так и метод сбора информации.

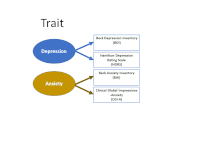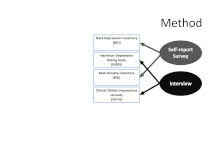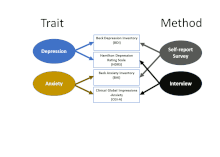
Используя наблюдаемые данные, можно изучить долю дисперсии, разделяемую между признаками и методами, чтобы получить представление о том, насколько специфичная для метода дисперсия вызвана методом измерения, а также оценить, насколько различим этот признак. по сравнению с другой чертой.

В идеале признак должен иметь большее значение, чем конкретный метод, выбранный для измерения. Например, если по одному показателю человек оценивается как находящийся в сильной депрессии, то другой показатель депрессии также должен дать высокие оценки. С другой стороны, люди, которые кажутся сильно подавленными по опроснику депрессии Бека, не обязательно должны иметь высокие оценки тревожности по опроснику тревожности Бека , поскольку предполагается, что они измеряют разные конструкты. Поскольку опросники были составлены одним и тем же человеком и схожи по стилю, некоторая корреляция может быть, но это сходство в методе не должно сильно влиять на баллы, поэтому корреляция между этими показателями различных характеристик должна быть низкой.

Анализ

Для анализа данных матрицы MTMM использовались различные статистические подходы. Стандартный метод Кэмпбелла и Фиске можно реализовать с помощью программы MTMM.EXE, доступной по адресу: https://web.archive.org/web/20160304173400/http://gim.med.ucla.edu/FacultyPages/Hays/utils . / Можно также использовать подтверждающий факторный анализ из-за сложностей учета всех данных в матрице. Савиловский я испытываю, однако учитывает все данные в матрице с помощью статистического теста без распределения на предмет тренда.

Пример модели измерения MTMM

Тест проводится путем сведения треугольников гетеропризнак-гетерометод и гетеропримет-монометод, а также диагоналей достоверности и надежности в матрицу из четырех уровней. Каждый уровень состоит из минимального, медианного и максимального значений. Нулевая гипотеза заключается в том, что эти значения неупорядочены, что проверяется против альтернативной гипотезы о возрастающей упорядоченной тенденции. Статистика теста находится путем подсчета количества инверсий (I). Критическое значение для альфа = 0,05 — 10, а для альфа = 0,01 — 14.

Одной из наиболее часто используемых моделей для анализа данных MTMM является модель True Score, предложенная Сарисом и Эндрюсом ( ). Модель True Score можно выразить с помощью следующих стандартизированных уравнений:

    1) Yij = rij TSij + eij* where:
         Yij is the standardized observed variable measured with the ith trait and jth method.
         rij is the reliability coefficient, which is equal to:
           rij = σYij / σTSij 
         TSij is the standardized true score variable
         eij* is the random error, which is equal to:
           eij* = eij / σYij
      
     Consequently:
       rij2 = 1 - σ2 (eij*) where:
         rij2 is the reliability

    2) TSij = vij Fi + mij Mj where:
         vij is the validity coefficient, which is equal to:
           vij = σFi / σTSij 
         Fi is the standardized latent factor for the ith variable of interest (or trait)
         mij is the method effect, which is equal to:
         mij = σMj / σTSij
         Mj is the standardized latent factor for the reaction to the jthmethod
      
     Consequently:
       vij2 = 1 - mij2 where:
         vij2 is the validity

    3) Yij = qijFi + rijmijMj + e* where:
         qij is the quality coefficient, which is equal to:
           qij = rij  •  vij
        
     Consequently:
       qij2 = rij2  •  vij2 = σ2Fi / σ2Yij where:
         qij2 is the quality

Предположения следующие:

     * The errors are random, thus the mean of the errors is zero: µe = E(e) = 0 
     * The random errors are uncorrelated with each other: cov(ei, ej) = E(ei ej) = 0 
     * The random errors are uncorrelated with the independent variables:  cov(TS, e) = E(TS e) = 0 ,  cov(F, e) = E(F e) = 0  and  cov(M, e) = E(M e) = 0  
     * The method factors are assumed to be uncorrelated with one another and with the trait factors: cov(F, M) = E(F M) = 0 

Как правило, респондент должен ответить как минимум на три различных показателя (т.е. характеристики), измеряемые с использованием как минимум трех разных методов. Эта модель использовалась для оценки качества тысяч вопросов опроса, в частности в рамках Европейского социального опроса .