Магнитная левитация

В эксперименте с готовыми комплектующими используется магнит, приклеенный к концу вращающегося мультитула. Его вращение заставляет второй магнит левитировать в миллиметрах от первого. ^[1]

Магнитная левитация ( маглев ) или магнитная подвеска — это метод, при котором объект подвешивается без какой-либо поддержки, кроме магнитных полей . Магнитная сила используется для противодействия воздействию гравитационной силы и любых других сил.

Двумя основными проблемами, связанными с магнитной левитацией, являются подъемные силы : обеспечение направленной вверх силы, достаточной для противодействия гравитации, и стабильность : обеспечение того, чтобы система не скользила или не переворачивалась самопроизвольно в конфигурацию, в которой подъемная сила нейтрализуется.

Магнитная левитация используется для поездов на магнитной подвеске , бесконтактной плавки , магнитных подшипников и для демонстрации продукции.

Поднимать

Магнитные материалы и системы способны притягивать или отталкивать друг друга с силой, зависящей от магнитного поля и площади магнитов. Например, простейшим примером подъемной силы может быть простой дипольный магнит, расположенный в магнитных полях другого дипольного магнита, ориентированный одинаковыми полюсами друг к другу, так что сила между магнитами отталкивает два магнита.

По существу, все типы магнитов использовались для создания подъемной силы для магнитной левитации; постоянные магниты , электромагниты , ферромагнетизм , диамагнетизм , сверхпроводящие магниты и магнетизм, обусловленный индуцированными токами в проводниках.

Чтобы рассчитать величину подъемной силы, магнитное давление можно определить .

Например, магнитное давление магнитного поля на сверхпроводник можно рассчитать по формуле:

P_{\text{mag}}={\frac {B^{2}}{2\mu _{0}}}

где $P_{\text{mag}}$ — сила на единицу площади в паскалях , $B$ — магнитное поле над сверхпроводником в теслах , а $\mu _{0}$ = 4π × 10 ⁻⁷ Н·Д ⁻² это проницаемость вакуума. ^[2]

Стабильность

Теорема Эрншоу доказывает, что при использовании только парамагнитных материалов (таких как ферромагнитное железо) статическая система не может устойчиво левитировать против силы тяжести. ^[3]

Например, простейший пример подъемной силы с отталкиванием двух простых дипольных магнитов очень нестабилен, поскольку верхний магнит может скользить вбок или переворачиваться, и оказывается, что никакая конфигурация магнитов не может обеспечить устойчивость.

Однако сервомеханизмы , использование диамагнитных материалов, сверхпроводимости или систем, использующих вихревые токи , позволяют достичь стабильности.

В некоторых случаях подъемная сила обеспечивается магнитным отталкиванием, а устойчивость обеспечивается механической опорой, несущей небольшую нагрузку. Это называется псевдолевитацией .

Статическая устойчивость

Статическая устойчивость означает, что любое небольшое отклонение от устойчивого равновесия заставляет результирующую силу толкать его обратно к точке равновесия.

Теорема Эрншоу убедительно доказала, что невозможно устойчиво левитировать, используя только статические, макроскопические и парамагнитные поля. Силы, действующие на любой парамагнитный объект в любых сочетаниях гравитационного , электростатического и магнитостатического полей, сделают положение объекта в лучшем случае неустойчивым хотя бы по одной оси, а он может находиться в неустойчивом равновесии по всем осям . Однако существует несколько возможностей сделать левитацию жизнеспособной, например, использование электронной стабилизации или диамагнитных материалов (поскольку относительная магнитная проницаемость меньше единицы). ^[4]); можно показать, что диамагнитные материалы стабильны по крайней мере по одной оси и могут быть стабильны по всем осям. Проводники могут иметь относительную проницаемость для переменных магнитных полей ниже единицы, поэтому некоторые конфигурации, использующие простые электромагниты с переменным током, являются самостабильными.

Динамическая устойчивость

Когда система левитации использует отрицательную обратную связь для поддержания равновесия путем гашения любых возможных колебаний, она достигает динамической устойчивости.

В случае статического магнитного поля магнитная сила является консервативной силой и, следовательно, не может иметь встроенного демпфирования. На практике многие схемы левитации являются маргинально устойчивыми и, если учитывать неидеальность физических систем, приводят к отрицательному затуханию. Это отрицательное затухание приводит к экспоненциально растущим колебаниям вокруг нестабильной точки равновесия магнитного поля, что неизбежно приводит к выбрасыванию левитирующего объекта из магнитного поля. ^[5]

Динамическая стабильность, с другой стороны, может быть достигнута путем вращения постоянного магнита, полюса которого немного отклоняются от плоскости вращения (так называемый наклон), с постоянной скоростью в пределах диапазона, который может удерживать другой дипольный магнит в воздухе. ^[6]^[7]

Чтобы схема магнитной левитации была устойчивой, отрицательную обратную связь от внешней системы управления для придания системе демпфирования можно также использовать . Этого можно добиться несколькими способами:

внешнее механическое демпфирование (в опоре), например торпеды , сопротивление воздуха и т.п.
гашение вихревых токов (проводящий металл под воздействием поля)
настроенные демпферы массы в левитирующем объекте
электромагниты, управляемые электроникой

Методы

Для успешной левитации и управления всеми 6 осями (степени свободы: 3 поступательные и 3 вращательные) можно использовать комбинацию постоянных магнитов и электромагнитов или диамагнетиков или сверхпроводников, а также притягивающих и отталкивающих полей. Согласно теореме Эрншоу, чтобы система могла успешно левитировать, должна присутствовать хотя бы одна устойчивая ось, но другие оси можно стабилизировать с помощью ферромагнетизма.

Основными из них, используемых в поездах на магнитной подвеске , являются сервостабилизированная электромагнитная подвеска (ЭМС) и электродинамическая подвеска (ЭДС).

Механическое ограничение (псевдолевитация)

При небольшом механическом ограничении устойчивости достижение псевдолевитации является относительно простым процессом.

Например, если два магнита механически закреплены вдоль одной оси и сильно отталкивают друг друга, это приведет к левитации одного из магнитов над другим.

Другая геометрия заключается в том, что магниты притягиваются, но не могут соприкоснуться с помощью натяжного элемента, такого как веревка или кабель.

Другим примером является центрифуга типа Zippe , в которой цилиндр подвешен под притягивающим магнитом и стабилизирован снизу игольчатым подшипником.

Другая конфигурация состоит из массива постоянных магнитов, установленных в ферромагнитном U-образном профиле и соединенных с ферромагнитной направляющей. Магнитный поток пересекает рельс в направлении, поперечном первой оси, и создает замкнутый контур на U-образном профиле. Такая конфигурация создает устойчивое равновесие вдоль первой оси, которое удерживает рельс в центре точки пересечения потока (минимальное магнитное сопротивление) и позволяет нести нагрузку магнитно. На другой оси система удерживается и центрируется механическими средствами, такими как колеса. ^[8]

Сервомеханизмы

Притяжение магнита фиксированной силы уменьшается с увеличением расстояния и увеличивается на более близких расстояниях. Это нестабильно. Для стабильной системы необходимо обратное: отклонения от стабильного положения должны подтолкнуть ее обратно к целевому положению.

Стабильная магнитная левитация может быть достигнута путем измерения положения и скорости левитирующего объекта и использования петли обратной связи , которая непрерывно регулирует один или несколько электромагнитов для корректировки движения объекта, образуя таким образом сервомеханизм .

Многие системы используют магнитное притяжение, тянущее вверх против силы тяжести, для систем такого типа, поскольку это придает некоторую внутреннюю боковую устойчивость, но некоторые используют комбинацию магнитного притяжения и магнитного отталкивания для толкания вверх.

Любая система представляет собой примеры электромагнитной подвески (EMS). В качестве очень простого примера, в некоторых демонстрациях настольной левитации используется этот принцип, и объект разрезает луч света или для измерения положения объекта используется метод датчика Холла. Электромагнит находится над левитирующим объектом; электромагнит выключается всякий раз, когда объект приближается слишком близко, и включается снова, когда он падает дальше. Такая простая система не очень надежна; существуют гораздо более эффективные системы контроля, но это иллюстрирует основную идею.

EMS Поезда на магнитной подушке основаны на таком виде левитации: поезд обволакивает рельсы и тянется вверх снизу. Сервоприводы удерживают его на постоянном расстоянии от гусеницы.

Индуцированные токи

Эти схемы работают за счет отталкивания по закону Ленца . Когда проводник находится в изменяющемся во времени магнитном поле, в проводнике возникают электрические токи, которые создают магнитное поле, вызывающее отталкивающий эффект.

Системы такого типа обычно демонстрируют присущую им стабильность, хотя иногда требуется дополнительное демпфирование.

Относительное движение между проводниками и магнитами

Если поднести основание, сделанное из очень хорошего электрического проводника, такого как медь , алюминий или серебро , близко к магниту, в проводнике индуцируется ( вихревой ) ток, который будет противодействовать изменениям поля и создавать противоположное поле, которое магнит будет отталкиваться ( закон Ленца ). При достаточно высокой скорости движения подвешенный магнит будет левитировать на металле или наоборот на подвешенном металле. Литцендрат, изготовленный из проволоки тоньше толщины кожи , на частотах, воспринимаемых металлом, работает гораздо эффективнее, чем сплошные проводники. Катушки в форме восьмерки можно использовать для поддержания выравнивания чего-либо. ^[9]

Особенно технологически интересный случай возникает, когда используется матрица Хальбаха вместо однополюсного постоянного магнита , поскольку это почти удваивает напряженность поля, что, в свою очередь, почти удваивает силу вихревых токов. Конечным результатом является увеличение подъемной силы более чем в три раза. Использование двух противоположных матриц Хальбаха еще больше увеличивает поле. ^[10]

Массивы Хальбаха также хорошо подходят для магнитной левитации и стабилизации гироскопов и шпинделей электродвигателей и генераторов .

Колеблющиеся электромагнитные поля

Проводник пропуская можно парить над электромагнитом (или наоборот), через него переменный ток . Это заставляет любой обычный проводник вести себя как диамагнит из-за вихревых токов , генерируемых в проводнике. ^[11]^[12] Поскольку вихревые токи создают собственные поля, противодействующие магнитному полю, проводящий объект отталкивается от электромагнита, и большинство силовых линий магнитного поля больше не проникают в проводящий объект.

Для этого эффекта требуются неферромагнитные, но высокопроводящие материалы, такие как алюминий или медь, поскольку ферромагнитные материалы также сильно притягиваются к электромагниту (хотя на высоких частотах поле все еще может вытесняться) и имеют тенденцию иметь более высокое удельное сопротивление, что приводит к меньшим вихревым токам. Опять же, литцендрат дает наилучшие результаты.

Этот эффект можно использовать для таких трюков, как левитация телефонной книги, спрятав внутри нее алюминиевую пластину.

При высоких частотах (несколько десятков килогерц или около того) и мощности в киловаттах небольшие количества металлов можно поднимать в воздух и плавить с помощью левитационной плавки без риска загрязнения металла тиглем. ^[13]

Одним из используемых источников осциллирующего магнитного поля является линейный асинхронный двигатель . Это можно использовать как для левитации, так и для придания движения.

Диамагнитно стабилизированная левитация

Теорема Ирншоу неприменима к диамагнетикам . Они ведут себя противоположно обычным магнитам из-за их относительной µ проницаемости r _< 1 (т.е. отрицательной магнитной восприимчивости ). Диамагнитная левитация может быть по своей природе стабильной.

Постоянный магнит можно стабильно подвешивать с помощью сильных постоянных магнитов и сильных диамагнитов различной конфигурации. При использовании сверхпроводящих магнитов левитацию постоянного магнита можно стабилизировать даже за счет небольшого диамагнетизма воды в пальцах человека. ^[14]

Диамагнитная левитация

Диамагнетизм — это свойство объекта, которое заставляет его создавать магнитное поле, противоположное внешнему магнитному полю, что приводит к отталкиванию материала магнитными полями. Диамагнитные материалы заставляют линии магнитного потока отклоняться от материала. В частности, внешнее магнитное поле изменяет орбитальную скорость электронов вокруг своих ядер, тем самым изменяя магнитный дипольный момент.

Согласно закону Ленца, это противодействует внешнему полю. Диамагнетиками называют материалы с магнитной проницаемостью менее µ ₀ (относительная проницаемость менее 1). Следовательно, диамагнетизм — это форма магнетизма, которая проявляется веществом только в присутствии внешнего магнитного поля. Обычно это довольно слабый эффект для большинства материалов, хотя сверхпроводники проявляют сильный эффект.

Прямая диамагнитная левитация

Вещество, являющееся диамагнетиком, отталкивает магнитное поле. свойствами объекта Все материалы обладают диамагнитными свойствами, но эффект очень слабый и обычно преодолевается парамагнитными или ферромагнитными , которые действуют противоположным образом. Любой материал, в котором диамагнитная составляющая сильнее, будет отталкиваться магнитом.

Диамагнитная левитация может использоваться для левитации очень легких кусков пиролитического графита или висмута над постоянным магнитом средней силы. Поскольку вода преимущественно диамагнитна, этот метод использовался для левитации капель воды и даже живых животных, таких как кузнечик, лягушка и мышь. ^[15] Однако необходимые для этого магнитные поля очень велики, обычно в диапазоне 16 Тл , и поэтому создают серьезные проблемы, если поблизости находятся ферромагнитные материалы. Для работы этого электромагнита, использованного в эксперименте по левитации лягушки, требовалась 4 МВт (4000000 Вт). мощность ^[15]^: 5

Минимальный критерий диамагнитной левитации: $B{\frac {dB}{dz}}=\mu _{0}\,\rho \,{\frac {g}{\chi }}$ , где:

$\chi$ магнитная восприимчивость
$\rho$ это плотность материала
$g$ - местное ускорение свободного падения (−9,8 м / с ² на Земле)
$\mu _{0}$ это проницаемость свободного пространства
$B$ магнитное поле
${\frac {dB}{dz}}$ – скорость изменения магнитного поля вдоль вертикальной оси.

Предполагая идеальные условия в направлении z соленоидного магнита:

Вода левитирует в $B{\frac {dB}{dz}}\approx 1400\ \mathrm {T^{2}/m}$
Графит левитирует в $B{\frac {dB}{dz}}\approx 375\ \mathrm {T^{2}/m} .$

Сверхпроводники

Сверхпроводники можно считать идеальными диамагнетиками , которые полностью исключают магнитные поля из-за эффекта Мейсснера при первоначальном формировании сверхпроводимости; таким образом, сверхпроводящую левитацию можно рассматривать как частный случай диамагнитной левитации. В сверхпроводнике II типа левитация магнита дополнительно стабилизируется за счет закрепления потока внутри сверхпроводника; это имеет тенденцию мешать сверхпроводнику двигаться относительно магнитного поля, даже если левитирующая система перевернута.

Эти принципы используются в EDS (электродинамической подвеске), сверхпроводящих подшипниках , маховиках и т. д.

Для левитации поезда требуется очень сильное магнитное поле. Поезда SCMaglev имеют сверхпроводящие магнитные катушки, но левитация SCMaglev не обусловлена эффектом Мейснера.

Ротационная стабилизация

Верх с логотипом Левитрон демонстрирует стабилизированную вращением магнитную левитацию.

Магнит или правильно собранный массив магнитов может стабильно левитировать против силы тяжести при гироскопической стабилизации путем вращения его в тороидальном поле, создаваемом базовым кольцом магнита (ов). Однако это работает только тогда, когда скорость прецессии находится между верхним и нижним критическими порогами - область устойчивости довольно узка как в пространстве, так и по необходимой скорости прецессии.

Первое открытие этого явления было сделано Роем М. Харриганом , изобретателем из Вермонта , который в 1983 году запатентовал на его основе левитационное устройство. ^[16] несколько устройств, использующих стабилизацию вращения (например, популярная игрушка с левитирующим верхом под брендом Levitron На основании этого патента было разработано ). Для университетских исследовательских лабораторий были созданы некоммерческие устройства, в которых обычно используются магниты, слишком мощные для безопасного взаимодействия с общественностью.

Сильная фокусировка

Теория Эрншоу применима только к статическим полям. Переменные магнитные поля, даже чисто переменные поля притяжения, ^[17] может обеспечить стабильность и ограничить траекторию магнитным полем, создавая эффект левитации.

Он используется в ускорителях частиц для удержания и подъема заряженных частиц, а также был предложен для поездов на магнитной подвеске. ^[17]

Использование

Известные применения магнитной левитации включают поезда на магнитной подвеске , бесконтактную плавку , магнитные подшипники и для демонстрации продукции. Более того, в последнее время к магнитной левитации начали обращаться в области микроботики .

Маглев транспорт

Маглев , или магнитная левитация , представляет собой систему транспорта, которая подвешивает, направляет и приводит в движение транспортные средства, преимущественно поезда, используя магнитную левитацию от очень большого количества магнитов для подъема и движения. Этот метод потенциально может быть быстрее, тише и плавнее, чем колесные общественного транспорта системы . Технология может превысить скорость 6400 км/ч (4000 миль/ч) при использовании в эвакуированном туннеле. ^[18] Если он не развернут в вакуумной трубе, мощность, необходимая для левитации, обычно не составляет особенно большого процента, и большая часть необходимой мощности используется для преодоления сопротивления воздуха , как и в любом другом высокоскоростном поезде.Некоторые прототипы транспортных средств Hyperloop на магнитной подвеске разрабатываются в рамках конкурса капсул Hyperloop в 2015–2016 годах, и, как ожидается, первые тестовые испытания в вакуумной трубе пройдут позднее в 2016 году. ^[19]

Самая высокая зарегистрированная скорость поезда на магнитной подвеске составляет 603 километра в час (374,69 миль в час), достигнутая в Японии 21 апреля 2015 года; На 28,2 км/ч быстрее обычного рекорда скорости TGV . Поезда Маглев существуют и планируются по всему миру. Известные проекты в Азии включают Центрально-Японской железнодорожной компании сверхпроводящий поезд на магнитной подвеске и поезд на магнитной подвеске в Шанхае , старейший коммерческий поезд на магнитной подвеске, который все еще находится в эксплуатации. В других странах Европы рассматривались различные проекты, и компания Northeast Maglev Северной Америки направлена на капитальный ремонт Северо-восточного коридора от JR Central с использованием технологии SCMaglev .

Магнитные подшипники

Левитация плавления

Электромагнитная левитация (ЭМЛ), запатентованная Муком в 1923 году. ^[20] — один из старейших методов левитации, используемый для экспериментов без контейнеров. ^[21] Техника левитирует предметы с помощью электромагнитов . Типичная катушка EML имеет перевернутую обмотку верхней и нижней частей, питаемую от радиочастотного источника питания.

Микроботика

В области микроботики были исследованы стратегии, использующие магнитную левитацию. В частности, было продемонстрировано, что с помощью такого метода можно достичь контроля над множеством агентов микромасштаба в пределах определенного рабочего пространства. ^[22] В нескольких исследованиях сообщается о реализации различных индивидуальных настроек для правильного получения желаемого контроля над микророботами. В лабораториях Philips специальная система клинического масштаба, объединяющая как постоянные магниты , так и электромагниты . в Гамбурге для выполнения магнитной левитации и трехмерной навигации одного магнитного объекта использовалась ^[23] Другая исследовательская группа интегрировала большее количество электромагнитов и, следовательно, больше магнитных степеней свободы , чтобы добиться независимого трехмерного управления несколькими объектами посредством магнитной левитации. ^[24]

Система ДМ3

Микроробот, использующий магнитную левитацию, уже много лет изучается SRI International (Стэнфордский исследовательский институт). ^[25] Эта небольшая многоагентная роботизированная система называется «Диамагнитная микроманипуляция» или система DM3. ^[26]^[27]^[28] DM3 содержит микроробота, построенного на магнитах, которые левитируют и перемещаются по поверхности приводной платформы печатной платы. Микроробот в этой системе был построен с использованием массива магнитов NdFeB, показанных на рисунке File:Microrobot Magnet Disposition.png . Размер магнитов варьируется в зависимости от версии, но обычно находится в диапазоне 1,4. ^[27]-2 ^[26] мм квадратной формы с меньшей высотой. Полюса магнитов были расположены в виде шахматной доски, чтобы соответствовать магнитному полю, создаваемому платформой печатной платы. Робот может быть построен разного размера в зависимости от размера массива. Прототипы, протестированные в статьях НИИ, в основном имеют размер 2*2, ^[26]^[27]^[29] 3*3, ^[27] и 5*5 ^[29] квадраты.

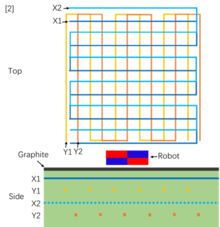
Плата приводной платформы была построена с несколькими слоями проводных дорожек, как при срабатывании звуковой катушки. На рисунке [1] показано , что на печатной плате имеется четыре слоя проводов, которые представляют собой два набора, расположенных перпендикулярно друг другу и обозначающих движение в направлениях X и Y. Сверху вниз порядок идет в формате XYXY, которые равномерно пересекают друг друга, и одни и те же оси переплетаются для управления срабатыванием. Поскольку сила, создаваемая каждым слоем, должна быть одинаковой в цепи, более глубоким слоям требуется более высокий ток для передачи той же магнитной силы роботам наверху. В НИИ использовался набор токов 0,25А, 0,33А, 0,5А и 0,7А. ^[26] Один квадрат вышеупомянутой 4-слойной системы действует как зона на платформе управления. ^[27] Это позволяет схеме легко управлять несколькими роботами в одной зоне, но каждый робот не может двигаться отдельно. Однако платформу можно разделить на несколько зон, что позволяет отдельно управлять роботами в разных зонах.

Наконец, тонкий слой пиролитического графита (500 мкм) действует как диамагнитный слой, расположенный сверху для обеспечения стабильной левитации. Тонкая медь (15 мкм), расположенная над графитом, использовалась в более ранних версиях. ^[26] системы гашения вихревых токов.

2D движение

Базовая система перемещения с 1 степенями свободы состоит из двух змеевидных направляющих, приводимых в действие индивидуально. ^[30]^[31] На рисунке показана схема путей следа и магнитный микроробот 3х3 сверху. В позиции номер 1 магниты находятся в положении равновесия, где плотность магнитного потока самая высокая, между двумя противоположными токами, идущими по одному и тому же пути следа.

При переходе от 1 к 2 первый путь трассировки отключается, а второй включается. Это заставляет магниты перемещаться в новое состояние равновесия, в сторону более высокой плотности магнитного потока.

Повторяя эту процедуру с противоположными токами на тех же траекториях, создается движение в нужном направлении. ^[32]

Чтобы найти скорость, необходимо проанализировать силы, действующие на микроробота (рис. [2] ). Предполагается, что микроробот левитирует, поэтому не возникает никакого принудительного трения, за исключением сопротивления воздуха, которое также не учитывается.

Сила, возникающая при взаимодействии магнитных моментов микроробота и плотности потока змеевидных дорожек, равна:

F=\nabla ({\overrightarrow {m}}\cdot {\overrightarrow {B}})

Вектор магнитного момента с учетом требований ориентации для диамагнитной левитации равен:

{\overrightarrow {m}}={\bigl (}{\begin{smallmatrix}0&0&{\frac {B_{r}V_{m}}{\mu _{0}}}\\\end{smallmatrix}}{\bigr )}

При этом вклад в поле B двух ближайших трасс составляет:

{\vec {B}}={\vec {B}}_{1}+{\vec {B}}_{2}=\ \mu _{0}{\frac {{\vec {I_{1}}}\times {\vec {r}}_{1}}{2\pi \left|{\vec {r}}_{1}\right|^{2}}}+\mu _{0}{\frac {{\vec {I_{2}}}\times {\vec {r}}_{2}}{2\pi \left|{\vec {r}}_{2}\right|^{2}}}

Поскольку для этого приближения ${\overrightarrow {m}}\cdot {\overrightarrow {B}}$ не зависит от y или z, их производные равны нулю и создается только сила в направлении x:

F_{x}={\frac {B_{r}V_{m}I}{2\pi }}{\frac {\partial }{\partial x}}\left({\frac {x-\Delta x_{0}}{(x-\Delta x_{0})^{2}+d^{2}}}+{\frac {x+\Delta x_{0}}{(x+\Delta x_{0})^{2}+d^{2}}}\right)

Это единственная сила, приложенная к магниту, и ее можно приравнять к массе робота, умноженной на его ускорение. Это уравнение можно проинтегрировать, чтобы найти скорость микроробота:

F_{x}=mv{\frac {dv}{dx}}

{\frac {B_{r}V_{m}I}{2\pi m}}\left({\frac {2\Delta x_{0}}{4\Delta x_{0}^{2}+d^{2}}}\right)={\frac {1}{2}}v_{max}^{2}

Введение в зависимость между объемом, массой и плотностью магнита. $V_{m}={\frac {m}{\rho _{m}}}$ в предыдущем уравнении отменяется масса, а это означает, что если добавить больше магнитов (количество N магнитов), сила будет увеличиваться линейно:

v_{max}={\sqrt {N{\frac {B_{r}I}{\pi \rho _{m}}}\left({\frac {2\Delta x_{0}}{4\Delta x_{0}^{2}+d^{2}}}\right)}}

Это выражение скорости робота как функции тока.

Для второй глубины резкости необходимо добавить больше трасс. Еще две переплетенные змеевидные дорожки необходимо добавить ниже существующих, повернув на 90 градусов, чтобы создавать силы в направлении Y. Интенсивность этих следов должна быть выше, чтобы учесть большее расстояние.

Левитация

Милли- и микророботами, левитирующими на диамагнитном поле, можно управлять и перемещать их силу практически с нулевым шумом, и их можно сделать внутренне стабильными. Таким образом, существует высокооптимизированное управление, использующее зональный или территориальный контроль. ^[33]

Диамагнитная левитация может оказать на микроробота два эффекта. Первый — это уменьшение трения скольжения, а второй — полная левитация микроробота. В центре внимания будет система полной левитации. Для создания пассивной левитации диамагнитный слой (например, графит) должен существовать в присутствии ферромагнетика (например, NdFeB). ^[34] Диамагнетики характеризуются отрицательной восприимчивостью, индуцированным магнитным моментом, противоположным внешнему магнитному полю. По этой причине они отталкиваются внешним магнитным полем и стремятся двигаться к минимуму поля. Эта сила отталкивания является результатом того, что диамагнетики имеют направление намагничивания, антипараллельное внешним магнитным полям.

Намагниченность диамагнитных материалов меняется в зависимости от приложенного магнитного поля, которое можно определить как:

M=\chi _{p}H

Где $H$ - напряженность магнитного поля и $\chi _{p}$ – безразмерная восприимчивость. Для объекта объёмом $V_{p}$ , индуцированный магнитный момент m может быть определен как:

{\overrightarrow {m}}=\chi _{p}{\frac {V_{p}}{\mu _{0}}}{\overrightarrow {B}}

Магнитная сила, действующая на объект, описывается как:

F_{m}={\frac {\chi _{p}V_{p}}{\mu _{0}}}\nabla ({\overrightarrow {B}}\cdot {\overrightarrow {B}})

Если объект имеет плотность $\rho _{p}$ и левитирует в среде с плотностью $\rho _{m}$ и магнитная восприимчивость $\chi _{m}$ Полная энергия объекта с магнитным и гравитационным составом равна:

E={\frac {\chi _{p}-\chi _{m}}{2\mu _{0}}}V_{p}({\overrightarrow {B}}\cdot {\overrightarrow {B}})+(\rho _{p}-\rho _{m})V_{p}gz

Так что результирующая сила становится:

\sum F={\frac {\chi _{p}-\chi _{m}}{2\mu _{0}}}V_{p}\nabla ({\overrightarrow {B}}\cdot {\overrightarrow {B}})+(\rho _{p}-\rho _{m})V_{p}g{\overrightarrow {k}}

Необходимым условием стабильности является:

\chi _{p}-\chi _{m}<0

Чтобы рассчитать всю диамагнитную силу, действующую на левитирующие материалы, необходимо учитывать каждый отдельный диполь диамагнитного материала. Диамагнитную силу для всего объема можно выразить как:

F_{m}={\frac {\chi _{p}}{\mu _{0}}}\iiint _{V_{p}}\nabla ({\overrightarrow {B}}\cdot {\overrightarrow {B}})dv

Сила диамагнитного отталкивания пропорциональна магнитной восприимчивости диамагнетиков. Для противодействия гравитации в магнитном поле предпочтительны материалы с сильным диамагнетизмом и легкими свойствами.

Роботы, левитирующие на феррожидкости

Некоторые эксперименты были проведены с использованием феррожидкостей для увеличения мощности и полезной нагрузки диамагнитных микророботов. Диамагнитная левитация кажется многообещающей из-за ее точного управления, нулевого трения и нулевого износа, но становится менее надежной при более высоких нагрузках, поскольку ее максимальное опорное давление составляет порядка 102. Следовательно, феррожидкости с максимальным опорным давлением порядка 2 x 104, были изучены для увеличения веса, который может вытянуть магнитная сила. Исследование Сюя [2] продемонстрировало, что микроробот, управляемый феррожидкостью, способен нести в 130 раз большую массу, чем его аналог с голым магнитом. Это будет применимо к макромасштабным роботам (5–15 г), которым необходимо нести более тяжелые полезные нагрузки. Однако при работе с феррожидкостями следует учитывать эффекты смачивания и испарения жидкости. На движение феррожидкости и скорость испарения влияет тип поверхности, на которой она лежит. Исследование [2] показало, что при скольжении феррожидкости по тефлоновой поверхности остается меньше капель феррожидкости, чем по графитовой поверхности.

Электромагнитное срабатывание с использованием катушек

Другим примером магнитного срабатывания является использование электромагнитных катушек для создания магнитного поля. Генерируя магнитное поле, электромагнитные катушки использовались в качестве инструмента для отталкивания/притягивания окружающих магнитов, что создает движение. Плоские катушки — это еще одна конфигурация катушек, которые используются в устройствах MEMS для генерации силы, а также в датчиках и микронасосах. Поскольку эти катушки плоские, они позволяют уменьшить объем устройства. Динамики представляют собой повседневный пример срабатывания с помощью электромагнитных катушек (рис. 2). Через катушку пропускают переменный ток, создавая магнитное поле. Это магнитное поле взаимодействует с постоянным магнитом и вызывает вибрацию диафрагмы динамика, которая вибрирует окружающий воздух, создавая звук.

Магнитное поле постоянных магнитов

Постоянные магниты не требуют внешнего источника питания, что делает их очень энергоэффективными и идеальными для таких применений, как магнитная левитация. Их относительная магнитная проницаемость $\mu _{r}$ очень близко к единице, а это значит, что они не искажают существенно внешне генерируемые магнитные поля.Магнитное поле в данной точке представляет собой суперпозицию полей, создаваемых всеми источниками тока. Магнитное поле постоянных магнитов можно рассчитать, используя эквивалентную плотность поверхностного тока, определяемую как:

$I'={\frac {dI}{ds}}={\frac {B_{r}}{\mu _{0}}}$

Здесь I' — эквивалентная плотность поверхностного тока, B_r — остаточное магнитное поле магнита, а μ_0 — проницаемость свободного пространства, определяемая формулой: $\mu _{0}=4\pi \times 10^{-7}\,{\text{(A/Tm)}}$

Плотность поверхностного тока I^' прямо пропорциональна остаточному магнитному полю B_r, которое является мерой остаточной намагниченности магнита после удаления внешнего магнитного поля. Это свойство имеет решающее значение для эффективности магнита в таких приложениях, как магнитная левитация, где важно поддерживать стабильное и сильное магнитное поле. Для расчета магнитного поля, создаваемого постоянными магнитами, мы можем использовать подход, основанный на законе Био-Савара, применяемом к прямоугольным токовым слоям конечного размера. Этот метод предполагает моделирование магнитов как совокупности таких листов, что позволяет рассчитать три компоненты магнитного поля B⃗_z в любой точке пространства. Применяя этот закон к прямоугольному токовому слою конечного размера, мы можем вычислить магнитное поле, интегрируя вклады всех токовых элементов внутри слоя. Для прямоугольного листа с поверхностной плотностью тока I' магнитное поле в точке z ⃗ можно определить путем суммирования вкладов от каждого бесконечно малого сегмента листа.Чтобы смоделировать постоянный магнит, мы рассматриваем его как стопку таких токовых слоев. Суммарное магнитное поле B _z в любой точке представляет собой суперпозицию полей, создаваемых каждым листом. Эта суперпозиция выражается математически как:

${\vec {B}}_{z}=\sum _{i}{\vec {B}}_{z,i}$

где ${\vec {B}}_{z,i}$ представляет собой вклад магнитного поля от i-го токового слоя. Этот метод обеспечивает комплексный способ расчета компонентов магнитного поля постоянных магнитов, позволяя точно моделировать их магнитное поведение в различных приложениях, таких как магнитная левитация, где точное распределение поля имеет решающее значение для стабильности и производительности.

Магнитное поле прямой нити с током.

Магнитное поле в точке ${\vec {r}}_{2}$ из-за нити, по которой течет ток I, начинается в положении ${\vec {r}}_{a}$ и заканчивается на ${\vec {r}}_{b}$ (рис. 3) дается законом Био-Савара

${\vec {B}}({\vec {r}}_{2})={\frac {\mu _{0}I}{4\pi }}\int {\frac {d{\vec {r}}_{1}\times ({\vec {r}}_{2}-{\vec {r}}_{1})}{|{\vec {r}}_{2}-{\vec {r}}_{1}|^{3}}}$

где ${\vec {r}}_{1}=(1-t){\vec {r}}_{a}+t{\vec {r}}_{b}$ (точка на нити 0<t<1) и ${\frac {d{\vec {r}}_{1}}{dt}}=-{\vec {r}}_{a}+{\vec {r}}_{b}$ . Уравнение может быть организовано как:

${\vec {B}}({\vec {r}}_{2})={\frac {\mu _{0}I}{4\pi }}\int {\frac {d{\vec {r}}_{1}\times ({\vec {r}}_{2}-{\vec {r}}_{1})}{|{\vec {r}}_{2}-{\vec {r}}_{1}|^{3}}}$

Такого, что мы можем написать $({\vec {B}}({\vec {r}}_{2})$ как:

${\vec {B}}({\vec {r}}_{2})={\frac {\mu _{0}I}{4\pi }}({\vec {r}}_{b}-{\vec {r}}_{a})\times ({\vec {r}}_{2}-{\vec {r}}_{a})\int _{0}^{1}{\frac {1}{[A-2tB+t^{2}C]^{3/2}}}\,dt$

с $A=({\vec {r}}_{2}-{\vec {r}}_{a})^{2}$ , $B=({\vec {r}}_{2}-{\vec {r}}_{a})\cdot ({\vec {r}}_{b}-{\vec {r}}_{a})$ , $C=({\vec {r}}_{b}-{\vec {r}}_{a})^{2}$

Наконец, магнитное поле прямой нити с током определяется как: ${B}({\vec {r}}_{2})={\frac {\mu _{0}I}{4\pi }}{\frac {{\vec {r}}_{b}-{\vec {r}}_{a}\times {\vec {r}}_{2}-{\vec {r}}_{a}}{AC-B^{2}}}(C-B-A-2B+C+B-A)$

Магнитное поле одного листа для постоянных магнитов

Для расчета поля листа (рис. 4) рассмотрим поле, создаваемое нитью, смещенной вбок вектором:

${\vec {p}}=\alpha ({\vec {r}}_{b}-{\vec {r}}_{a})\times {\vec {n}}$

${\vec {p}}$ перпендикулярен нити, а α — соотношение сторон листа. Ширина листа составляет: $w=\alpha ({\vec {r}}_{b}-{\vec {r}}_{a})=\alpha C$

Поле смещенной нити затем определяется путем замены параметров A, B и C их s-зависимыми аналогами, определяемыми по формуле:

$A(s)=({\vec {r}}_{2}-{\vec {r}}_{a}-s{\vec {p}})^{2}$

$B_{s}=({\vec {r}}_{2}-{\vec {r}}_{a}-s{\vec {p}})\cdot ({\vec {r}}_{b}-{\vec {r}}_{a})$

$C_{s}=({\vec {r}}_{b}+s{\vec {p}}-{\vec {r}}_{a}-s{\vec {p}})^{2}=C$

Затем распределяем ток равномерно по ширине листа:

$I=I'w={\frac {B_{r}}{\mu _{0}}}\alpha C$

Магнитное поле конечного токового слоя можно определить как

${\vec {B}}({\vec {r}}_{2})={\frac {B_{r}\alpha C}{4\pi }}\int _{-1/2}^{1/2}{\frac {({\vec {r}}_{b}-{\vec {r}}_{a})\times ({\vec {r}}_{2}-{\vec {r}}_{a}-s{\vec {p}})}{[A(s)C-B(s)^{2}]^{3/2}}}ds$

Такого, что мы можем написать ${\vec {B}}({\vec {r}}_{2})$ как:

${\vec {B}}({\vec {r}}_{2})={\frac {B_{r}\alpha C}{4\pi }}\int _{-1/2}^{1/2}\left[{\frac {({\vec {r}}_{b}-{\vec {r}}_{a})\times ({\vec {r}}_{2}-{\vec {r}}_{a}+\alpha C{\vec {n}})}{R_{1}+P_{1}}}+{\frac {({\vec {r}}_{b}-{\vec {r}}_{a})\times ({\vec {r}}_{2}-{\vec {r}}_{a}+\alpha C{\vec {n}})}{R_{2}+P_{2}}}\right]ds$

где $R_{1}=a_{1}+b_{1}s+c_{1}s^{2}$ , $a_{1}=AC-2BC+C^{2}$ , $b_{1}=-2CD$ , $c_{1}=\alpha ^{2}C^{2}$ , $R_{2}=a_{2}+b_{2}s+c_{2}s^{2}$ , $a_{2}=AC,b_{2}=-2CD=b_{1},c_{2}=\alpha ^{2}C^{2}=c_{1},P_{1}=-(B-C)^{2},P_{2}=-B^{2}$

Наконец, магнитное поле конечного токового слоя организовано как:

${\vec {B}}({\vec {r}}_{2})={\frac {B_{r}\alpha C}{4\pi }}\left[{\frac {({\vec {r}}_{b}-{\vec {r}}_{a})\times ({\vec {r}}_{2}-{\vec {r}}_{a})}{C-B}}J_{1}+BJ_{3}\right]+{\frac {B_{r}\alpha ^{2}C^{2}}{4\pi }}\left[{\frac {C-B}{J_{2}+BJ_{4}}}\right]{\vec {n}}$

где $J_{1}=\int _{-1/2}^{1/2}{\frac {1}{R_{1}+P_{1}}}ds,J_{2}=\int _{-1/2}^{1/2}{\frac {s}{R_{1}+P_{1}}}ds,J_{3}=\int _{-1/2}^{1/2}{\frac {1}{R_{2}+P_{2}}}ds,J_{4}=\int _{-1/2}^{1/2}{\frac {s}{R_{2}+P_{2}}}ds$

Получив магнитное поле, извлеченное из магнита, мы теперь пытаемся использовать его в приложении для левитации. Диамагнетики обладают уникальным свойством: они отталкивают магнитные поля, стремясь к областям с минимальной напряженностью поля. Такое поведение позволяет диамагнитным материалам левитировать над сильными магнитными полями - явление, ярко продемонстрированное в эксперименте с левитирующей лягушкой. Понимание этих фундаментальных принципов проложило путь к инновационным технологиям, таким как магнитная левитация в микророботах. Милли- и микророботы с диамагнитной левитацией обеспечивают точное управление и минимальный силовой шум, обеспечивая внутреннюю стабильность и эффективный контроль зон. Используя диамагнитную левитацию, эти роботы испытывают меньшее трение скольжения и могут достичь полной левитации в сочетании с диамагнитным слоем, например графитом, в присутствии ферромагнетика, такого как NdFeB. Диамагнетики, характеризующиеся отрицательной восприимчивостью и индуцированным магнитным моментом, противодействующим внешнему полю, отталкиваются магнитными полями, естественно тяготея к минимумам поля. Это отталкивание возникает из-за того, что направление намагничивания диамагнетиков антипараллельно внешнему полю, что обеспечивает пассивную левитацию и облегчает усовершенствованные стратегии управления.

Для левитации магнита суммарные силы, действующие на него в направлении Z, должны быть равны нулю. Схема свободного тела показана ниже:

Для левитации диамагнитной частицы должно применяться следующее уравнение:

$\ F={\frac {\chi _{p}-\chi _{m}}{2\mu _{0}}}V_{p}\nabla ({\vec {B}}\cdot {\vec {B}})+(\rho _{p}-\rho _{m})V_{p}gz$

Диамагнитная частица с плотностью $\rho _{p}$ и магнитная восприимчивость $\chi _{p}$ левитирует в среде с плотностью $\rho _{m}$ и магнитная восприимчивость $\chi _{m}$ . В этом случае результирующая сила будет равна нулю только тогда, когда: $\chi _{p}-\chi _{m}<0$ . Отличие нашей задачи в том, что мы пытаемся левитировать магнит на листе диамагнитной поверхности, а не наоборот. Поэтому в приведенной выше формулировке должно быть обоснование:

$F={\frac {\chi _{\text{dia}}}{2\mu _{0}}}V_{\text{dia}}\nabla ({\vec {B}}\cdot {\vec {B}})+(\rho _{\text{mag}}-\rho _{\text{air}})V_{\text{mag}}gz$

Параметр $V_{\text{dia}}$ является спорным, и необходимы дальнейшие исследования, чтобы определить его фактическое значение, потому что, когда магнит является левитирующим объектом, создаваемое им магнитное поле не будет охватывать весь объем диамагнитного поверхностного листа. Необходимо рассчитать глубину проникновения и эффективную поверхность. (обратите внимание, что χ_dia отрицательно, поэтому уравнение имеет хотя бы одно решение).

На диаграмме свободного тела выше видны две другие силы Fx и Fy. Чтобы объяснить это, давайте рассмотрим термин ∇(B ⃗⋅B ⃗) и расширим его. Плотность магнитного поля — это векторная функция, отображаемая, как показано ниже:

${\vec {B}}(x,y,z)=B_{x}(x,y,z){\hat {x}}+B_{y}(x,y,z){\hat {y}}+B_{z}(x,y,z){\hat {z}}$

${\vec {B}}\cdot {\vec {B}}=B_{x}^{2}(x,y,z)+B_{y}^{2}(x,y,z)+B_{z}^{2}(x,y,z)$

$\nabla ({\vec {B}}\cdot {\vec {B}})=\left({\frac {\partial }{\partial x}}+{\frac {\partial }{\partial y}}+{\frac {\partial }{\partial z}}\right)(B_{x}^{2}(x,y,z)+B_{y}^{2}(x,y,z)+B_{z}^{2}(x,y,z))$

$=2\left(B_{x}{\frac {\partial B_{x}}{\partial x}}+B_{y}{\frac {\partial B_{y}}{\partial x}}+B_{z}{\frac {\partial B_{z}}{\partial x}}\right){\hat {x}}+\left(B_{x}{\frac {\partial B_{x}}{\partial y}}+B_{y}{\frac {\partial B_{y}}{\partial y}}+B_{z}{\frac {\partial B_{z}}{\partial y}}\right){\hat {y}}+\left(B_{x}{\frac {\partial B_{x}}{\partial z}}+B_{y}{\frac {\partial B_{y}}{\partial z}}+B_{z}{\frac {\partial B_{z}}{\partial z}}\right){\hat {z}}$

Третий термин, который $B_{x}{\frac {\partial B_{x}}{\partial z}}+B_{y}{\frac {\partial B_{y}}{\partial z}}+B_{z}{\frac {\partial B_{z}}{\partial z}}$ следует сравнивать с силой тяжести. Чтобы магнит имел стабильную левитацию, первый и второй член должны быть равны нулю. Необходимо дальнейшее расследование.

Чтобы найти расстояние, с которого левитирует магнит, необходимо решить уравнение, приведенное ниже:

$\left|{\frac {\chi _{\text{dia}}}{2\mu _{0}}}V_{\text{dia}}\left(B_{x}{\frac {\partial B_{x}}{\partial z}}+B_{y}{\frac {\partial B_{y}}{\partial z}}+B_{z}{\frac {\partial B_{z}}{\partial z}}\right)\right|=(\rho _{\text{mag}}-\rho _{\text{air}})V_{\text{mag}}g$

Основываясь на том, какой магнит мы выбираем, мы можем определить поведение Магнитного поля в космосе. ${\vec {B}}(x,y,z)$ . Для численного решения уравнения и использования магнитного поля как векторной функции (а это так и есть) будет az=d, который:

$\left(B_{x}{\frac {\partial B_{x}}{\partial z}}+B_{y}{\frac {\partial B_{y}}{\partial z}}+B_{z}{\frac {\partial B_{z}}{\partial z}}\right)_{x,y,d}=(\rho _{\text{mag}}-\rho _{text{air}})V_{\text{mag}}g$

Для упрощения |B_(x,y) |≪|B_z |,|(∂B_z)/∂x|≪ |(∂B_z)/∂z| ,|(∂B_z)/∂y|≪ |(∂B_z)/∂z|, задача перед ее решением, статья (Р. Энгель–Герберт и Т. Хеседаль, «Расчет магнитного поля рассеяния одноосного магнитного домен», сообщил:

Что облегчит расчеты:

$\left|{\chi _{\text{dia}}}{V_{\text{dia}}}\right|B_{z}{\frac {\partial B_{z}}{\partial z}}_{x,y,d}=(\rho _{\text{mag}}-\rho _{\text{air}})V_{\text{mag}}g$

В конце, рассчитав Bz по уравнениям, объясненным ранее, и вложив их в это, мы сможем решить проблему левитации, выяснив, на какой высоте работает приведенное выше уравнение.

Эффекты диамагнитной левитации

Диамагнитная левитация может оказать на микроробота два эффекта: уменьшить трение скольжения и полностью поднять микроробота. Для достижения пассивной левитации должен присутствовать диамагнитный слой, такой как графит, в сочетании с ферромагнитным материалом, таким как неодим-железо-бор (NdFeB). Взаимодействие между этими материалами создает силу отталкивания, которая может противодействовать гравитации и другим силам, действующим на микроробота.

Параметры и результаты моделирования

Рассмотрим массив магнитов NdFeB размером 3x3, каждый с размером полюса 1 мм и толщиной 0,4 мм. Моделирование диамагнитной силы в зависимости от расстояния от поверхности магнита показано на рис. 5. Это моделирование дает критическое представление о профиле силы, испытываемой микророботом на различной высоте над магнитной решеткой.

Кроме того, на рис. 6 показаны $B_{z}$ составляющая (плотность магнитного потока в направлении z) на поверхности магнита. Этот компонент предназначен для понимания распределения магнитного поля, которое напрямую влияет на левитацию и устойчивость микроробота.

Исторические верования

Легенды о магнитной левитации были распространены в древние и средневековые времена, и их распространение из римского мира на Ближний Восток, а затем в Индию было задокументировано ученым-классиком Данстаном Лоу. ^[35]^[36] Самым ранним известным источником является Плиний Старший (первый век нашей эры), который описал архитектурные планы железной статуи, которая должна была быть подвешена на магните к своду храма в Александрии. Во многих последующих сообщениях описывались левитирующие статуи, реликвии или другие объекты символического значения, а версии легенды появлялись в различных религиозных традициях, включая христианство, ислам, буддизм и индуизм. В одних случаях их интерпретировали как божественные чудеса, а в других описывали как явления природы, ложно выдаваемые за чудеса; Один из примеров последнего исходит от святого Августина, который ссылается на подвешенную на магните статую в своей книге «Город Божий» ( ок. 410 г. н. э. ). Другой общей чертой этих легенд, по мнению Лоу, является объяснение исчезновения объекта, часто связанное с его уничтожением неверующими в результате актов нечестия. Хотя сейчас считается, что само это явление физически невозможно, как это впервые признал Сэмюэл Эрншоу. В 1842 году истории о магнитной левитации сохранились до наших дней, одним из ярких примеров является легенда о подвешенном памятнике в Храме Солнца в Конарке в Восточной Индии.

История

1839 г. Теорема Эрншоу показала, что электростатическая левитация не может быть стабильной; более поздняя теорема была распространена на магнитостатическую левитацию другими.
1913 В марте 1912 года Эмиль Бачелет получил патент на свое «левитирующее передающее устройство» (патент № 1020942) на систему электромагнитной подвески.
1933 г. Супердиамагнетизм Вальтер Мейснер и Роберт Оксенфельд ( эффект Мейснера ).
1934 Герман Кемпер «Монорельсовое транспортное средство без колес». Патент Рейха № 643316.
1939 г. Расширение Браунбека показало, что магнитная левитация возможна с диамагнитными материалами.
1939 г. Алюминиевая пластина Бедфорда, Пера и Тонкса, помещенная на две концентрические цилиндрические катушки, демонстрирует стабильную 6-осевую левитацию. ^[37]
1961 Джеймс Р. Пауэлл и его коллега из BNL Гордон Дэнби. Электродинамическая левитация с использованием сверхпроводящих магнитов и катушек в форме восьмерки с нулевым потоком. ^[9]
1970-е годы. Магнитная левитация, стабилизированная спином. Рой М. Харриган.
1974 Магнитная река Эрик Лэйтуэйт и другие
1979 г. сверхскоростной поезд перевез пассажиров.
1981 Первая система магнитной левитации с одним тросом, представленная публично ( Том Шеннон , Компас любви, коллекция Musee d'Art Moderne de la Ville de Paris).
1984 г. Низкоскоростной шаттл на магнитной подвеске в Бирмингеме Эрик Лейтуэйт и другие.
1997 Живая лягушка, левитирующая на диамагнитном поле, Андре Гейм. ^[15]
1999 Электродинамическая левитация с постоянными магнитами Inductrack (General Atomics)
2000 г. В Китае была успешно разработана первая в мире испытательная машина HTS на магнитной подвеске «Century». ^[38]
2024 г. Первый пассивный поезд на магнитной подвеске был представлен и продемонстрирован в Вероне, Италия . ^[39]

См. также

Акустическая левитация
Аэродинамическая левитация
Электростатическая левитация
Циклотроны левитируют и циркулируют заряженные частицы в магнитном поле.
Inductrack - конкретная система, основанная на матрицах Хальбаха и индуктивных контактных петлях.
Запустить цикл
Левитрон
Линейный двигатель
Магнитный подшипник
Магнитное кольцо вращается
Линия Нагахори Цуруми-рёкути
Оптическая левитация
Быстрые перевозки с использованием линейного двигателя
StarTram — это экстремальное предложение по левитации с помощью сверхпроводников на расстояние в несколько километров.
В центрифуге типа Zippe используется магнитный подъемник и механическая игла для обеспечения стабильности.

Ссылки

^ Хермансен, Иоахим Марко; Лауст Дурхуус, Фредерик; Франдсен, Кэтрин; Беледжиа, Марко; Р. Х. Бахл, Кристиан; Бьорк, Расмус (13 октября 2023 г.). «Магнитная левитация за счет вращения» . Физ. Преподобный Прил . 20 (4): 044036–044051. arXiv : 2305.00812 . Бибкод : 2023PhRvP..20d4036H . doi : 10.1103/PhysRevApplied.20.044036 . S2CID 258426320 . Проверено 23 октября 2023 г.
^ Лекция 19 MIT 8.02 Электричество и магнетизм, весна 2002 г.
^ Невежество = Маглев = Блаженство На протяжении 150 лет учёные считали, что стабильная магнитная левитация невозможна. Затем появился Рой Харриган. Теодор Грей Опубликовано 2 февраля 2004 г.
^ Браунбек, В. (1939). «Свободно плавающие тела в электрическом и магнитном полях». Журнал физики . 112 (11): 753–763. Бибкод : 1939ZPhy..112..753B . дои : 10.1007/BF01339979 . S2CID 123618279 .
^ Роте, ДМ; Иган Цай (2002). «Обзор динамической устойчивости систем подвески на магнитной подвеске с силой отталкивания» . Транзакции IEEE по магнетизму . 38 (2): 1383. Бибкод : 2002ITM....38.1383R . дои : 10.1109/20.996030 .
^ Уджар, Хамди (март 2021 г.). «Свободное от полярности магнитное отталкивание и магнитно-связанное состояние» . Симметрия . 13 (3): 442. arXiv : 2009.07082 . Бибкод : 2021Symm...13..442U . дои : 10.3390/sym13030442 . ISSN 2073-8994 .
^ Хермансен, Иоахим Марко; Лауст Дурхуус, Фредерик; Франдсен, Кэтрин; Беледжиа, Марко; Р. Х. Бахл, Кристиан; Бьорк, Расмус (13 октября 2023 г.). «Магнитная левитация за счет вращения» . Физ. Преподобный Прил . 20 (4): 044036–044051. arXiv : 2305.00812 . Бибкод : 2023PhRvP..20d4036H . doi : 10.1103/PhysRevApplied.20.044036 . S2CID 258426320 . Проверено 23 октября 2023 г.
^ «Он летает над существующими путями!? Итальянский стартап разрабатывает новый автомобиль на магнитной подвеске» 23 февраля 2018 г.
^ Jump up to: ^а ^б «Биография Джеймса Р. Пауэлла Maglev2000» . Архивировано из оригинала 8 сентября 2012 г. Проверено 15 февраля 2017 г.
^ С&ТР | Ноябрь 2003 г.: Маглев на пути развития городского транспорта. Архивировано 10 октября 2012 г. в Wayback Machine . Llnl.gov (07.11.2003). Проверено 12 июля 2013 г.
^ Томпсон, Марк Т. Магнитная левитация вихревых токов, модели и эксперименты . (PDF). Проверено 12 июля 2013 г.
^ Левитирующий шар — левитация алюминиевой сферы диаметром 1 см . Sprott.Physics.wisc.edu. Проверено 12 июля 2013 г.
^ Местел, Эй Джей (2006). «Магнитная левитация жидких металлов». Журнал механики жидкости . 117 : 27–43. Бибкод : 1982JFM...117...27M . дои : 10.1017/S0022112082001505 . S2CID 123638123 .
^ Диамагнитно-стабилизированная магнитная левитация . (PDF). Проверено 12 июля 2013 г.
^ Jump up to: ^а ^б ^с «Лягушка, которая научилась летать» . Университет Радбауд в Неймегене . Проверено 19 октября 2010 г. О рассказе Гейма о диамагнитной левитации см. Гейм, Андрей. «Магнетизм каждого» (PDF) . (688 КБ) . Физика сегодня . Сентябрь 1998 г., стр. 36–39. Проверено 19 октября 2010 г. Об эксперименте с Берри см. Berry, MV ; Гейм, Андре. (1997). «О летающих лягушках и левитронах» (PDF) . Архивировано (PDF) из оригинала 3 ноября 2010 г. (228 КБ) . Европейский журнал физики 18 : 307–313. Проверено 19 октября 2010 г.
^ Патент США 4382245 , Харриган, Рой М., «Устройство левитации», выдан 3 мая 1983 г.
^ Jump up to: ^а ^б Халл, младший (1989). «Привлекательная левитация для высокоскоростного наземного транспорта с большим дорожным просветом и стабилизацией переменного уклона» . Транзакции IEEE по магнетизму . 25 (5): 3272–3274. Бибкод : 1989ITM....25.3272H . дои : 10.1109/20.42275 .
^ Трансатлантический Маглев | Популярная наука . Popsci.com. Проверено 12 июля 2013 г.
^ Лаварс, Ник (31 января 2016 г.). «Инженеры MIT выиграли конкурс модулей Hyperloop и протестируют прототип в середине 2016 года» . Проверено 1 февраля 2016 г.
^ Мук, О. Патент Германии №. 42204 (30 октября 1923 г.)
^ Нордин, Пол С.; Вебер, Дж. К. Ричард и Абади, Йохан Г. (2000). «Свойства высокотемпературных расплавов при использовании левитации» . Чистая и прикладная химия . 72 (11): 2127–2136. дои : 10.1351/pac200072112127 .
^ Сюй, Тяньтянь; Ю, Цзянфань; Ян, Сяохуэй; Чхве, Хонсу; Чжан, Ли (2015). «Управление движением микророботов на основе магнитного привода: обзор» . Микромашины . 6 (9): 1346–1364. дои : 10.3390/mi6091346 . ISSN 2072-666X .
^ Дао, Мин; Рамер, Юрген; Стенинг, Кристиан; Гляйх, Бернхард (2018). «Дистанционное магнитное срабатывание с использованием системы клинического масштаба» . ПЛОС ОДИН . 13 (3): e0193546. Бибкод : 2018PLoSO..1393546R . дои : 10.1371/journal.pone.0193546 . ISSN 1932-6203 . ПМЦ 5832300 . ПМИД 29494647 .
^ Онгаро, Федерико; Пане, Стефано; Шегги, Стефано; Мисра, Сартак (2019). «Разработка электромагнитной установки для независимого трехмерного управления парами идентичных и неидентичных микророботов» . Транзакции IEEE в робототехнике . 35 (1): 174–183. дои : 10.1109/TRO.2018.2875393 . ISSN 1552-3098 . S2CID 59619195 .
^ Пелрин, RE (сентябрь 1989 г.). «Микроробототехника на магнитной подвеске: подход к высокоинтегрированным системам малого производства» . Седьмой международный симпозиум по технологиям электронного производства IEEE/CHMT . стр. 273–276. дои : 10.1109/EMTS.1989.68988 .
^ Jump up to: ^а ^б ^с ^д ^и Пелрин, Рон; Вонг-Фой, Аннджо; Маккой, Брайан; Холеман, Деннис; Махони, Рич; Майерс, Грег; Херсон, Джим; Лоу, Том (май 2012 г.). «Диамагнитно левитирующие роботы: подход к массово-параллельным робототехническим системам с необычными свойствами движения» . Международная конференция IEEE по робототехнике и автоматизации . стр. 739–744. дои : 10.1109/ICRA.2012.6225089 .
^ Jump up to: ^а ^б ^с ^д ^и Пелрин, Рон; Сюй, Аллен; Коуэн, Крегг; Вонг-Фой, Анджо (июль 2017 г.). Мультиагентные системы с использованием диамагнитных микроманипуляций — От плавающих роев до мобильных сенсоров . Международная конференция по манипулированию, автоматизации и робототехнике в малых масштабах . Монреаль, Квебек: IEEE. стр. 1–6. дои : 10.1109/МАРСС.2017.8001930 . ISBN 978-1-5386-0346-8 .
^ Сюй, Аллен; Чжао, Хуэйхуа; Годро, Мартин; Фой, Аннджо Вонг; Пелрин, Рон (апрель 2020 г.). «Магнитная роевая платформа милли-роботов: сертифицированный барьер безопасности, недорогой испытательный стенд» . Письма IEEE по робототехнике и автоматизации . 5 (2): 2913–2920. дои : 10.1109/LRA.2020.2974713 . ISSN 2377-3766 . S2CID 212645507 .
^ Jump up to: ^а ^б Сюй, Аллен; Чу, Уильям; Коуэн, Крегг; Маккой, Брайан; Вонг-Фой, Аннджо; Пелрин, Рон; Лейк, Джозеф; Баллард, Джошуа; Рэндалл, Джон (01 июня 2018 г.). «Диамагнитно левитирующие Милли-роботы для гетерогенной трехмерной сборки». Журнал микробио-робототехники . 14 (1): 1–16. дои : 10.1007/s12213-018-0103-4 . ISSN 2194-6426 . S2CID 255530844 .
^ Иржи, Кутан; Франтишек, Мах (сентябрь 2017 г.). «Магнитоуправляемое воздействие ферромагнитных тел на плоские поверхности: численное моделирование и экспериментальная проверка». 18-я Международная конференция по вычислительным проблемам электротехники . IEEE. дои : 10.1109/cpee.2017.8093067 .
^ Юррик, Мартин; Кутан, Иржи; Влчек, Иржи; Мах, Франтишек (май 2019 г.). «Уменьшение неопределенности позиционирования при срабатывании с магнитным управлением на плоских поверхностях» . Международная конференция по робототехнике и автоматизации . стр. 1772–1778. дои : 10.1109/ICRA.2019.8794190 .
^ Пелрин, Р.; Сюй, А.; Вонг-Фой, А. (июль 2019 г.). «Методы и результаты вращения диамагнитных роботов с использованием трансляционных конструкций» . Международная конференция по манипулированию, автоматизации и робототехнике в малых масштабах . стр. 1–6. дои : 10.1109/MARSS.2019.8860975 .
^ Гао, ЦюХуа; Ян, Хан; Цзоу, Хунсян; Ли, ВэньБо; Пэн, ЧжиКе; Мэн, Гуан; Чжан, Вэньмин (01 января 2021 г.). «Магнитная левитация с использованием диамагнетизма: механизм, применение и перспективы». Наука Китайские технологические науки . 64 (1): 44–58. Бибкод : 2021ScChE..64...44G . дои : 10.1007/s11431-020-1550-1 . ISSN 1869-1900 . S2CID 255192417 .
^ Пелрин, RE (февраль 1990 г.). «Комнатная температура, разомкнутая левитация микроустройств с использованием диамагнитных материалов» . Труды IEEE по микроэлектромеханическим системам, исследование микроструктур, датчиков, приводов, машин и роботов . стр. 34–37. дои : 10.1109/MEMSYS.1990.110242 .
^ «Данстан Лоу» . сайт доктора Данстана Лоу . Проверено 30 мая 2019 г.
^ Лоу, Данстан (2016). «Приостановить неверие: магнитная левитация в древности и средневековье» (PDF) . Классическая античность . 35 : 247–278. дои : 10.1525/ca.2016.35.2.247 . Проверено 30 мая 2019 г.
^ Лейтуэйт, ER (1975). «Линейные электрические машины — личный взгляд». Труды IEEE . 63 (2): 250–290. Бибкод : 1975IEEEP..63..250L . дои : 10.1109/PROC.1975.9734 . S2CID 20400221 .
^ Ван, Цзясу; Ван Сую; и др. (2002). «Первая в мире испытательная машина на магнитной подвеске из высокотемпературного сверхпроводника, загружающая человека». Физика C: Сверхпроводимость и ее приложения . 378–381: 809–814. Бибкод : 2002PhyC..378..809W . дои : 10.1016/S0921-4534(02)01548-4 .
^ Верона, Путешествие (15 марта 2024 г.). «Первый в мире поезд на пассивной ферромагнитной левитации был представлен в Вероне» . Путешествие по Вероне . Проверено 17 марта 2024 г.

Внешние ссылки

Поезда Маглев ^{[ постоянная мертвая ссылка ]} В аудиослайд-шоу Национальной лаборатории сильных магнитных полей обсуждаются магнитная левитация, эффект Мейснера, захват магнитного потока и сверхпроводимость.
Магнитная левитация – наука – это весело
Эксперимент по магнитной (сверхпроводящей) левитации (YouTube)
Демонстрация сверхпроводящей левитации
Видеогалерея Маглева
Как можно левитировать предметы на магните?
Левитирующий алюминиевый шар (колеблющееся поле)
Инструкции по созданию демонстрации магнитной подвески с оптическим триггером и обратной связью
Видео диамагнитно левитирующих объектов, в том числе лягушек и кузнечиков.
Бесщеточный солнечный двигатель на магнитной левитации Ларри Спринга Mendocino
Демонстрация левитации в классе...
Установка подвески MAGLEV 25 кг.
Управление подвеской MAGLEV массой 25 кг с помощью классической стратегии управления
Подвеска MAGLEV массой 25 кг с использованием стратегии управления с обратной связью от государства
Лягушки левитируют в достаточно сильном магнитном поле
Пример левитации с механическими ограничениями

[1] Хермансен, Иоахим Марко; Лауст Дурхуус, Фредерик; Франдсен, Кэтрин; Беледжиа, Марко; Р. Х. Бахл, Кристиан; Бьорк, Расмус (13 октября 2023 г.). «Магнитная левитация за счет вращения» . Физ. Преподобный Прил . 20 (4): 044036–044051. arXiv : 2305.00812 . Бибкод : 2023PhRvP..20d4036H . doi : 10.1103/PhysRevApplied.20.044036 . S2CID 258426320 . Проверено 23 октября 2023 г.

[2] Лекция 19 MIT 8.02 Электричество и магнетизм, весна 2002 г.

[3] Невежество = Маглев = Блаженство На протяжении 150 лет учёные считали, что стабильная магнитная левитация невозможна. Затем появился Рой Харриган. Теодор Грей Опубликовано 2 февраля 2004 г.

[4] Браунбек, В. (1939). «Свободно плавающие тела в электрическом и магнитном полях». Журнал физики . 112 (11): 753–763. Бибкод : 1939ZPhy..112..753B . дои : 10.1007/BF01339979 . S2CID 123618279 .

[5] Роте, ДМ; Иган Цай (2002). «Обзор динамической устойчивости систем подвески на магнитной подвеске с силой отталкивания» . Транзакции IEEE по магнетизму . 38 (2): 1383. Бибкод : 2002ITM....38.1383R . дои : 10.1109/20.996030 .

[rotatingmagnet-6] Уджар, Хамди (март 2021 г.). «Свободное от полярности магнитное отталкивание и магнитно-связанное состояние» . Симметрия . 13 (3): 442. arXiv : 2009.07082 . Бибкод : 2021Symm...13..442U . дои : 10.3390/sym13030442 . ISSN 2073-8994 .

[7] Хермансен, Иоахим Марко; Лауст Дурхуус, Фредерик; Франдсен, Кэтрин; Беледжиа, Марко; Р. Х. Бахл, Кристиан; Бьорк, Расмус (13 октября 2023 г.). «Магнитная левитация за счет вращения» . Физ. Преподобный Прил . 20 (4): 044036–044051. arXiv : 2305.00812 . Бибкод : 2023PhRvP..20d4036H . doi : 10.1103/PhysRevApplied.20.044036 . S2CID 258426320 . Проверено 23 октября 2023 г.

[8] «Он летает над существующими путями!? Итальянский стартап разрабатывает новый автомобиль на магнитной подвеске» 23 февраля 2018 г.

[bio-9] Jump up to: ^а ^б «Биография Джеймса Р. Пауэлла Maglev2000» . Архивировано из оригинала 8 сентября 2012 г. Проверено 15 февраля 2017 г.

[10] С&ТР | Ноябрь 2003 г.: Маглев на пути развития городского транспорта. Архивировано 10 октября 2012 г. в Wayback Machine . Llnl.gov (07.11.2003). Проверено 12 июля 2013 г.

[11] Томпсон, Марк Т. Магнитная левитация вихревых токов, модели и эксперименты . (PDF). Проверено 12 июля 2013 г.

[12] Левитирующий шар — левитация алюминиевой сферы диаметром 1 см . Sprott.Physics.wisc.edu. Проверено 12 июля 2013 г.

[13] Местел, Эй Джей (2006). «Магнитная левитация жидких металлов». Журнал механики жидкости . 117 : 27–43. Бибкод : 1982JFM...117...27M . дои : 10.1017/S0022112082001505 . S2CID 123638123 .

[14] Диамагнитно-стабилизированная магнитная левитация . (PDF). Проверено 12 июля 2013 г.

[geim-15] Jump up to: ^а ^б ^с «Лягушка, которая научилась летать» . Университет Радбауд в Неймегене . Проверено 19 октября 2010 г. О рассказе Гейма о диамагнитной левитации см. Гейм, Андрей. «Магнетизм каждого» (PDF) . (688 КБ) . Физика сегодня . Сентябрь 1998 г., стр. 36–39. Проверено 19 октября 2010 г. Об эксперименте с Берри см. Berry, MV ; Гейм, Андре. (1997). «О летающих лягушках и левитронах» (PDF) . Архивировано (PDF) из оригинала 3 ноября 2010 г. (228 КБ) . Европейский журнал физики 18 : 307–313. Проверено 19 октября 2010 г.

[16] Патент США 4382245 , Харриган, Рой М., «Устройство левитации», выдан 3 мая 1983 г.

[alt-17] Jump up to: ^а ^б Халл, младший (1989). «Привлекательная левитация для высокоскоростного наземного транспорта с большим дорожным просветом и стабилизацией переменного уклона» . Транзакции IEEE по магнетизму . 25 (5): 3272–3274. Бибкод : 1989ITM....25.3272H . дои : 10.1109/20.42275 .

[18] Трансатлантический Маглев | Популярная наука . Popsci.com. Проверено 12 июля 2013 г.

[mit20160201-19] Лаварс, Ник (31 января 2016 г.). «Инженеры MIT выиграли конкурс модулей Hyperloop и протестируют прототип в середине 2016 года» . Проверено 1 февраля 2016 г.

[20] Мук, О. Патент Германии №. 42204 (30 октября 1923 г.)

[21] Нордин, Пол С.; Вебер, Дж. К. Ричард и Абади, Йохан Г. (2000). «Свойства высокотемпературных расплавов при использовании левитации» . Чистая и прикладная химия . 72 (11): 2127–2136. дои : 10.1351/pac200072112127 .

[XuYu2015-22] Сюй, Тяньтянь; Ю, Цзянфань; Ян, Сяохуэй; Чхве, Хонсу; Чжан, Ли (2015). «Управление движением микророботов на основе магнитного привода: обзор» . Микромашины . 6 (9): 1346–1364. дои : 10.3390/mi6091346 . ISSN 2072-666X .

[DaoRahmer2018-23] Дао, Мин; Рамер, Юрген; Стенинг, Кристиан; Гляйх, Бернхард (2018). «Дистанционное магнитное срабатывание с использованием системы клинического масштаба» . ПЛОС ОДИН . 13 (3): e0193546. Бибкод : 2018PLoSO..1393546R . дои : 10.1371/journal.pone.0193546 . ISSN 1932-6203 . ПМЦ 5832300 . ПМИД 29494647 .

[OngaroPane2019-24] Онгаро, Федерико; Пане, Стефано; Шегги, Стефано; Мисра, Сартак (2019). «Разработка электромагнитной установки для независимого трехмерного управления парами идентичных и неидентичных микророботов» . Транзакции IEEE в робототехнике . 35 (1): 174–183. дои : 10.1109/TRO.2018.2875393 . ISSN 1552-3098 . S2CID 59619195 .

[25] Пелрин, RE (сентябрь 1989 г.). «Микроробототехника на магнитной подвеске: подход к высокоинтегрированным системам малого производства» . Седьмой международный симпозиум по технологиям электронного производства IEEE/CHMT . стр. 273–276. дои : 10.1109/EMTS.1989.68988 .

[:0-26] Jump up to: ^а ^б ^с ^д ^и Пелрин, Рон; Вонг-Фой, Аннджо; Маккой, Брайан; Холеман, Деннис; Махони, Рич; Майерс, Грег; Херсон, Джим; Лоу, Том (май 2012 г.). «Диамагнитно левитирующие роботы: подход к массово-параллельным робототехническим системам с необычными свойствами движения» . Международная конференция IEEE по робототехнике и автоматизации . стр. 739–744. дои : 10.1109/ICRA.2012.6225089 .

[:1-27] Jump up to: ^а ^б ^с ^д ^и Пелрин, Рон; Сюй, Аллен; Коуэн, Крегг; Вонг-Фой, Анджо (июль 2017 г.). Мультиагентные системы с использованием диамагнитных микроманипуляций — От плавающих роев до мобильных сенсоров . Международная конференция по манипулированию, автоматизации и робототехнике в малых масштабах . Монреаль, Квебек: IEEE. стр. 1–6. дои : 10.1109/МАРСС.2017.8001930 . ISBN 978-1-5386-0346-8 .

[28] Сюй, Аллен; Чжао, Хуэйхуа; Годро, Мартин; Фой, Аннджо Вонг; Пелрин, Рон (апрель 2020 г.). «Магнитная роевая платформа милли-роботов: сертифицированный барьер безопасности, недорогой испытательный стенд» . Письма IEEE по робототехнике и автоматизации . 5 (2): 2913–2920. дои : 10.1109/LRA.2020.2974713 . ISSN 2377-3766 . S2CID 212645507 .

[:2-29] Jump up to: ^а ^б Сюй, Аллен; Чу, Уильям; Коуэн, Крегг; Маккой, Брайан; Вонг-Фой, Аннджо; Пелрин, Рон; Лейк, Джозеф; Баллард, Джошуа; Рэндалл, Джон (01 июня 2018 г.). «Диамагнитно левитирующие Милли-роботы для гетерогенной трехмерной сборки». Журнал микробио-робототехники . 14 (1): 1–16. дои : 10.1007/s12213-018-0103-4 . ISSN 2194-6426 . S2CID 255530844 .

[30] Иржи, Кутан; Франтишек, Мах (сентябрь 2017 г.). «Магнитоуправляемое воздействие ферромагнитных тел на плоские поверхности: численное моделирование и экспериментальная проверка». 18-я Международная конференция по вычислительным проблемам электротехники . IEEE. дои : 10.1109/cpee.2017.8093067 .

[31] Юррик, Мартин; Кутан, Иржи; Влчек, Иржи; Мах, Франтишек (май 2019 г.). «Уменьшение неопределенности позиционирования при срабатывании с магнитным управлением на плоских поверхностях» . Международная конференция по робототехнике и автоматизации . стр. 1772–1778. дои : 10.1109/ICRA.2019.8794190 .

[32] Пелрин, Р.; Сюй, А.; Вонг-Фой, А. (июль 2019 г.). «Методы и результаты вращения диамагнитных роботов с использованием трансляционных конструкций» . Международная конференция по манипулированию, автоматизации и робототехнике в малых масштабах . стр. 1–6. дои : 10.1109/MARSS.2019.8860975 .

[33] Гао, ЦюХуа; Ян, Хан; Цзоу, Хунсян; Ли, ВэньБо; Пэн, ЧжиКе; Мэн, Гуан; Чжан, Вэньмин (01 января 2021 г.). «Магнитная левитация с использованием диамагнетизма: механизм, применение и перспективы». Наука Китайские технологические науки . 64 (1): 44–58. Бибкод : 2021ScChE..64...44G . дои : 10.1007/s11431-020-1550-1 . ISSN 1869-1900 . S2CID 255192417 .

[34] Пелрин, RE (февраль 1990 г.). «Комнатная температура, разомкнутая левитация микроустройств с использованием диамагнитных материалов» . Труды IEEE по микроэлектромеханическим системам, исследование микроструктур, датчиков, приводов, машин и роботов . стр. 34–37. дои : 10.1109/MEMSYS.1990.110242 .

[35] «Данстан Лоу» . сайт доктора Данстана Лоу . Проверено 30 мая 2019 г.

[36] Лоу, Данстан (2016). «Приостановить неверие: магнитная левитация в древности и средневековье» (PDF) . Классическая античность . 35 : 247–278. дои : 10.1525/ca.2016.35.2.247 . Проверено 30 мая 2019 г.

[personalView-37] Лейтуэйт, ER (1975). «Линейные электрические машины — личный взгляд». Труды IEEE . 63 (2): 250–290. Бибкод : 1975IEEEP..63..250L . дои : 10.1109/PROC.1975.9734 . S2CID 20400221 .

[38] Ван, Цзясу; Ван Сую; и др. (2002). «Первая в мире испытательная машина на магнитной подвеске из высокотемпературного сверхпроводника, загружающая человека». Физика C: Сверхпроводимость и ее приложения . 378–381: 809–814. Бибкод : 2002PhyC..378..809W . дои : 10.1016/S0921-4534(02)01548-4 .

[39] Верона, Путешествие (15 марта 2024 г.). «Первый в мире поезд на пассивной ферромагнитной левитации был представлен в Вероне» . Путешествие по Вероне . Проверено 17 марта 2024 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]