Постоянно-рекурсивная последовательность

Последовательность Фибоначчи является константно-рекурсивной: каждый элемент последовательности представляет собой сумму двух предыдущих.

Диаграмма Хассе некоторых подклассов константно-рекурсивных последовательностей, упорядоченных по включению

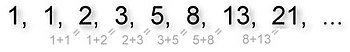
В математике последовательность бесконечная чисел ​ $s_{0},s_{1},s_{2},s_{3},\ldots$ называется константно-рекурсивным, если он удовлетворяет уравнению вида

$$s_{n}=c_{1}s_{n-1}+c_{2}s_{n-2}+\dots +c_{d}s_{n-d},$$

для всех $n\geq d$, где $c_{i}$ являются константами . Уравнение называется линейным рекуррентным соотношением .Эта концепция также известна как линейная рекуррентная последовательность , линейно-рекурсивная последовательность , линейно-рекуррентная последовательность или C-конечная последовательность .

Например, последовательность Фибоначчи

$0,1,1,2,3,5,8,13,\ldots$,

является константно-рекурсивным, поскольку удовлетворяет линейной рекуррентности $F_{n}=F_{n-1}+F_{n-2}$: каждое число в последовательности представляет собой сумму двух предыдущих. Другие примеры включают мощность двух последовательностей. $1,2,4,8,16,\ldots$, где каждое число представляет собой сумму удвоенного предыдущего числа, а квадратов чисел последовательность $0,1,4,9,16,25,\ldots$. Все арифметические прогрессии , все геометрические прогрессии и все многочлены являются константно-рекурсивными. Однако не все последовательности являются константно-рекурсивными; например, факториал последовательность $1,1,2,6,24,120,\ldots$ не является постоянно-рекурсивным.

Константно-рекурсивные последовательности изучаются в комбинаторике и теории конечных разностей . Они также возникают в алгебраической теории чисел из-за связи последовательности с многочленными корнями ; при анализе алгоритмов - как время выполнения простых рекурсивных функций ; и в теории формальных языков подсчитывают строки до заданной длины , где в обычном языке . Постоянно-рекурсивные последовательности замыкаются при выполнении важных математических операций, таких как почленное сложение , почленное умножение и произведение Коши .

Теорема Скулема -Малера-Леха утверждает, что нули константно-рекурсивной последовательности имеют регулярно повторяющуюся (в конечном итоге периодическую) форму. Проблема Скулема , которая требует алгоритма для определения того, имеет ли линейная рекуррентность хотя бы один ноль, является нерешенной проблемой в математике .

Определение

— Постоянно-рекурсивная последовательность это любая последовательность целых , рациональных , алгебраических , действительных или комплексных чисел. $s_{0},s_{1},s_{2},s_{3},\ldots$ (написано как $(s_{n})_{n=0}^{\infty }$ в качестве сокращения), удовлетворяющий формуле вида

$$s_{n}=c_{1}s_{n-1}+c_{2}s_{n-2}+\dots +c_{d}s_{n-d},$$

для всех $n\geq d,$ для некоторых фиксированных коэффициентов $c_{1},c_{2},\dots ,c_{d}$ в той же области, что и последовательность (целые числа, рациональные числа, алгебраические числа, действительные числа или комплексные числа).Уравнение называется линейной рекуррентностью с постоянными коэффициентами порядка d .Порядок . последовательности — это наименьшее целое положительное число $d$ такая, что последовательность удовлетворяет повторению порядка d , или $d=0$ для всюду нулевой последовательности.

Приведенное выше определение допускает в конечном итоге периодические последовательности, такие как $1,0,0,0,\ldots$ и $0,1,0,0,\ldots$. Некоторые авторы требуют, чтобы $c_{d}\neq 0$, что исключает такие последовательности.

Примеры

Избранные примеры целочисленных константно-рекурсивных последовательностей

Имя	Заказ ( $d$  )	Первые несколько значений	Рецидив (для $n\geq d$ )	Генерирующая функция	ОЭИС
Нулевая последовательность	0	0, 0, 0, 0, 0, 0, ...	$s_{n}=0$	${\frac {0}{1}}$	А000004
Одна последовательность	1	1, 1, 1, 1, 1, 1, ...	$s_{n}=s_{n-1}$	${\frac {1}{1-x}}$	А000012
Характеристическая функция $\{0\}$	1	1, 0, 0, 0, 0, 0, ...	$s_{n}=0$	${\frac {1}{1}}$	А000007
Полномочия двух	1	1, 2, 4, 8, 16, 32, ...	$s_{n}=2s_{n-1}$	${\frac {1}{1-2x}}$	А000079
Степени −1	1	1, −1, 1, −1, 1, −1, ...	$s_{n}=-s_{n-1}$	${\frac {1}{1+x}}$	А033999
Характеристическая функция $\{1\}$	2	0, 1, 0, 0, 0, 0, ...	$s_{n}=0$	${\frac {x}{1}}$	А063524
Десятичное расширение 1/6	2	1, 6, 6, 6, 6, 6, ...	$s_{n}=s_{n-1}$	${\frac {1+5x}{1-x}}$	А020793
Десятичное расширение 1/11	2	0, 9, 0, 9, 0, 9, ...	$s_{n}=s_{n-2}$	${\frac {9x}{1-x^{2}}}$	А010680
Неотрицательные целые числа	2	0, 1, 2, 3, 4, 5, ...	$s_{n}=2s_{n-1}-s_{n-2}$	${\frac {x}{(1-x)^{2}}}$	А001477
Нечетные положительные целые числа	2	1, 3, 5, 7, 9, 11, ...	$s_{n}=2s_{n-1}-s_{n-2}$	${\frac {1+x}{(1-x)^{2}}}$	А005408
Числа Фибоначчи	2	0, 1, 1, 2, 3, 5, 8, 13, ...	$s_{n}=s_{n-1}+s_{n-2}$	${\frac {x}{1-x-x^{2}}}$	А000045
Числа Лукаса	2	2, 1, 3, 4, 7, 11, 18, 29, ...	$s_{n}=s_{n-1}+s_{n-2}$	${\frac {2-x}{1-x-x^{2}}}$	А000032
Числа Пелла	2	0, 1, 2, 5, 12, 29, 70, ...	$s_{n}=2s_{n-1}+s_{n-2}$	${\frac {x}{1-2x-x^{2}}}$	А000129
Степени двойки, чередующиеся с нулями	2	1, 0, 2, 0, 4, 0, 8, 0, ...	$s_{n}=2s_{n-2}$	${\frac {1}{1-2x^{2}}}$	А077957
Обратный к 6-му круговому многочлену	2	1, 1, 0, −1, −1, 0, 1, 1, ...	$s_{n}=s_{n-1}-s_{n-2}$	${\frac {1}{1-x+x^{2}}}$	А010892
Треугольные числа	3	0, 1, 3, 6, 10, 15, 21, ...	$s_{n}=3s_{n-1}-3s_{n-2}+s_{n-3}$	${\frac {x}{(1-x)^{3}}}$	А000217

Последовательности Фибоначчи и Лукаса

Последовательность чисел Фибоначчи 0, 1, 1, 2, 3, 5, 8, 13, ... является константно-рекурсивной второго порядка, поскольку она удовлетворяет рекуррентному правилу $F_{n}=F_{n-1}+F_{n-2}$ с $F_{0}=0,F_{1}=1$. Например, $F_{2}=F_{1}+F_{0}=1+0=1$ и $F_{6}=F_{5}+F_{4}=5+3=8$. Последовательность чисел Люка 2, 1, 3, 4, 7, 11, ... удовлетворяет той же повторяемости, что и последовательность Фибоначчи, но с начальными условиями. $L_{0}=2$ и $L_{1}=1$. В более общем смысле, каждая последовательность Люка является константно-рекурсивной второго порядка.

Арифметические прогрессии

Для любого $a$ и любой $r\neq 0$, арифметическая прогрессия $a,a+r,a+2r,\ldots$ является константно-рекурсивным порядка 2, поскольку удовлетворяет условию $s_{n}=2s_{n-1}-s_{n-2}$. Обобщая это, см. полиномиальные последовательности ниже.

Геометрические прогрессии

Для любого $a\neq 0$ и $r$, геометрическая прогрессия $a,ar,ar^{2},\ldots$ является константно-рекурсивным порядка 1, поскольку удовлетворяет условию $s_{n}=rs_{n-1}$. Сюда входит, например, последовательность 1, 2, 4, 8, 16,..., а также последовательность рациональных чисел. ${\textstyle 1,{\frac {1}{2}},{\frac {1}{4}},{\frac {1}{8}},{\frac {1}{16}},...}$.

В конечном итоге периодические последовательности

Последовательность, которая в конечном итоге является периодической с длиной периода $\ell$ является постоянно-рекурсивным, поскольку удовлетворяет условию $s_{n}=s_{n-\ell }$ для всех $n\geq d$, где порядок $d$ — длина начального сегмента, включая первый повторяющийся блок. Примерами таких последовательностей являются 1, 0, 0, 0, ... (порядок 1) и 1, 6, 6, 6, ... (порядок 2).

Полиномиальные последовательности

Последовательность, определяемая полиномом $s_{n}=a_{0}+a_{1}n+a_{2}n^{2}+\cdots +a_{d}n^{d}$ является постоянно-рекурсивным. Последовательность удовлетворяет повторению порядка $d+1$ (где $d$ — степень полинома), с коэффициентами, заданными соответствующим элементом биномиального преобразования . Первые несколько таких уравнений:

$s_{n}=1\cdot s_{n-1}$ для полинома степени 0 (т. е. постоянного)

$s_{n}=2\cdot s_{n-1}-1\cdot s_{n-2}$ для полинома степени 1 или меньше,

$s_{n}=3\cdot s_{n-1}-3\cdot s_{n-2}+1\cdot s_{n-3}$ для полинома степени 2 или меньше, и

$s_{n}=4\cdot s_{n-1}-6\cdot s_{n-2}+4\cdot s_{n-3}-1\cdot s_{n-4}$ для полинома степени 3 или ниже.

Последовательность, подчиняющаяся уравнению порядка d, также подчиняется всем уравнениям более высокого порядка. Эти тождества можно доказать разными способами, в том числе с помощью теории конечных разностей . Любая последовательность $d+1$ целые, действительные или комплексные значения могут использоваться в качестве начальных условий для константно-рекурсивной последовательности порядка. $d+1$. Если начальные условия лежат на многочлене степени $d-1$ или меньше, то константно-рекурсивная последовательность также подчиняется уравнению более низкого порядка.

Перечисление слов в обычном языке

Позволять $L$ быть регулярным языком , и пусть $s_{n}$ быть числом слов длины $n$ в $L$. Затем $(s_{n})_{n=0}^{\infty }$ является постоянно-рекурсивным. Например, $s_{n}=2^{n}$ для языка всех двоичных строк, $s_{n}=1$ для языка всех одинарных строк и $s_{n}=F_{n+2}$ для языка всех двоичных строк, не имеющих двух последовательных. В более общем смысле, любая функция, принимаемая взвешенным автоматом в унарном алфавите. $\Sigma =\{a\}$ над полукольцом $(\mathbb {R} ,+,\times )$ (которое по сути является кольцом , и даже полем ) константно-рекурсивно.

Другие примеры

Последовательности чисел Якобсталя , чисел Падована , чисел Пелла и чисел Перрена. являются постоянно-рекурсивными.

Непримеры

Факториальная ​ последовательность $1,1,2,6,24,120,720,\ldots$ не является постоянно-рекурсивным. В более общем смысле, каждая константно-рекурсивная функция асимптотически ограничена экспоненциальной функцией (см. #Характеризация в замкнутой форме ), и последовательность факториалов растет быстрее, чем это.

Каталонская последовательность $1,1,2,5,14,42,132,\ldots$ не является постоянно-рекурсивным. Это связано с тем, что производящая функция каталонских чисел не является рациональной функцией (см. #Определения эквивалентов ).

Эквивалентные определения

С точки зрения матриц

Основная статья: Матрица сопутствующих товаров

$F_{n}={\begin{bmatrix}0&1\end{bmatrix}}{\begin{bmatrix}1&1\\1&0\end{bmatrix}}^{n}{\begin{bmatrix}1\\0\end{bmatrix}}.$

Определение последовательности Фибоначчи с помощью матриц.

Последовательность $(s_{n})_{n=0}^{\infty }$ является константно-рекурсивным, порядка меньше или равного $d$ тогда и только тогда, когда это можно записать как

$s_{n}=uA^{n}v$

где $u$ это $1\times d$ вектор, $A$ это $d\times d$ матрица и $v$ это $d\times 1$ вектор, где элементы происходят из той же области (целые, рациональные числа, алгебраические числа, действительные числа или комплексные числа), что и исходная последовательность. Конкретно, $v$ можно считать первым $d$ значения последовательности, $A$ линейное преобразование , которое вычисляет $s_{n+1},s_{n+2},\ldots ,s_{n+d}$ от $s_{n},s_{n+1},\ldots ,s_{n+d-1}$, и $u$ вектор $[0,0,\ldots ,0,1]$.

В терминах неоднородных линейных рекуррентов

Основная статья: Линейная рекуррентность с постоянными коэффициентами § Преобразование к однородной форме

Неоднородный	Однородный
$s_{n}=1+s_{n-1}$	$s_{n}=2s_{n-1}-s_{n-2}$
$s_{0}=0$	$s_{0}=0;s_{1}=1$

Определение последовательности натуральных чисел $s_{n}=n$, используя неоднородную рекуррентность и эквивалентную однородную версию.

Неоднородная линейная рекуррентность — это уравнение вида

$s_{n}=c_{1}s_{n-1}+c_{2}s_{n-2}+\dots +c_{d}s_{n-d}+c$

где $c$ является дополнительной константой. Любая последовательность, удовлетворяющая неоднородной линейной рекуррентности, является константно-рекурсивной. Это связано с тем, что вычитание уравнения для $s_{n-1}$ из уравнения для $s_{n}$ дает однородную повторяемость для $s_{n}-s_{n-1}$, из которого мы можем решить $s_{n}$ чтобы получить

${\begin{aligned}s_{n}=&(c_{1}+1)s_{n-1}\\&+(c_{2}-c_{1})s_{n-2}+\dots +(c_{d}-c_{d-1})s_{n-d}\\&-c_{d}s_{n-d-1}.\end{aligned}}$

С точки зрения производящих функций

$\sum _{n=0}^{\infty }F_{n}x^{n}={\frac {x}{1-x-x^{2}}}.$

Определение последовательности Фибоначчи с помощью производящей функции.

Последовательность является константно-рекурсивной именно тогда, когда ее производящая функция

$\sum _{n=0}^{\infty }s_{n}x^{n}=s_{0}+s_{1}x^{1}+s_{2}x^{2}+s_{3}x^{3}+\cdots$

это рациональная функция $p(x)\,/\,q(x)$, где $p$ и $q$ являются полиномами и $q(0)=1$. При этом порядок последовательности является минимальным $d$ такой, что он имеет такую ​​форму с ${\text{deg }}q(x)\leq d$ и ${\text{deg }}p(x)<d$.

Знаменатель – это многочлен, полученный из вспомогательного многочлена путем изменения порядка коэффициентов , а числитель определяется начальными значениями последовательности:

$\sum _{n=0}^{\infty }s_{n}x^{n}={\frac {b_{0}+b_{1}x^{1}+b_{2}x^{2}+\dots +b_{d-1}x^{d-1}}{1-c_{1}x^{1}-c_{2}x^{2}-\dots -c_{d}x^{d}}},$

где

$b_{n}=s_{n}-c_{1}s_{n-1}-c_{2}s_{n-2}-\dots -c_{d}s_{n-d}.$

Из сказанного выше следует, что знаменатель $q(x)$ должен быть многочленом, не делящимся на $x$ (и, в частности, ненулевое).

В терминах пространств последовательностей

$\{(an+b)_{n=0}^{\infty }:a,b\in \mathbb {R} \}$

Двумерное векторное пространство последовательностей, порожденных последовательностью $s_{n}=n$.

Последовательность $(s_{n})_{n=0}^{\infty }$ является константно-рекурсивным тогда и только тогда, когда множество последовательностей

$\left\{(s_{n+r})_{n=0}^{\infty }:r\geq 0\right\}$

содержится в пространстве последовательностей ( векторном пространстве последовательностей), размерность которого конечна. То есть, $(s_{n})_{n=0}^{\infty }$ в конечномерном подпространстве содержится $\mathbb {C} ^{\mathbb {N} }$ закрыто под оператором левого сдвига .

Такая характеристика обусловлена ​​тем, что порядок $d$ линейное рекуррентное соотношение можно понимать как доказательство линейной зависимости между последовательностями $(s_{n+r})_{n=0}^{\infty }$ для $r=0,\ldots ,d$. Расширение этого аргумента показывает, что порядок последовательности равен размерности пространства последовательностей, созданного $(s_{n+r})_{n=0}^{\infty }$ для всех $r$.

Характеристика в закрытой форме

Для вывода замкнутой формы см. Линейную рекуррентность с постоянными коэффициентами § Общее решение .

$F_{n}={\frac {1}{\sqrt {5}}}(1.618\ldots )^{n}-{\frac {1}{\sqrt {5}}}(-0.618\ldots )^{n}$

Характеристика в закрытой форме последовательности Фибоначчи ( формула Бине )

Постоянно-рекурсивные последовательности допускают следующую уникальную замкнутой формы характеристику с использованием экспоненциальных полиномов : каждую константно-рекурсивную последовательность можно записать в виде

$s_{n}=z_{n}+k_{1}(n)r_{1}^{n}+k_{2}(n)r_{2}^{n}+\cdots +k_{e}(n)r_{e}^{n},$

для всех $n\geq 0$, где

• Термин $z_{n}$ представляет собой последовательность, которая равна нулю для всех $n\geq d$ (где $d$ – порядок последовательности);
• Условия $k_{1}(n),k_{2}(n),\ldots ,k_{e}(n)$ являются комплексными полиномами; и
• Условия $r_{1},r_{2},\ldots ,r_{k}$ являются отдельными комплексными константами.

Эта характеристика точна: каждая последовательность комплексных чисел, которую можно записать в указанной выше форме, является константно-рекурсивной.

Например, число Фибоначчи $F_{n}$ записывается в таком виде по формуле Бине :

$F_{n}={\frac {1}{\sqrt {5}}}\varphi ^{n}-{\frac {1}{\sqrt {5}}}\psi ^{n},$

где $\varphi =(1+{\sqrt {5}})\,/\,2\approx 1.61803\ldots$ это золотое сечение и $\psi =-1\,/\,\varphi$. Это корни уравнения $x^{2}-x-1=0$. В этом случае, $e=2$, $z_{n}=0$ для всех $n$, $k_{1}(n)=k_{2}(n)=1\,/\,{\sqrt {5}}$ оба являются постоянными полиномами, $r_{1}=\varphi$, и $r_{2}=\psi$.

Термин $z_{n}$ нужен только тогда, когда $c_{d}\neq 0$; если $c_{d}=0$ затем он исправляет тот факт, что некоторые начальные значения могут быть исключениями из общего повторения. В частности, $z_{n}=0$ для всех $n\geq d$.

Комплексные числа $r_{1},\ldots ,r_{n}$ являются корнями характеристического полинома рекуррентности:

$x^{d}-c_{1}x^{d-1}-\dots -c_{d-1}x-c_{d}$

коэффициенты которого такие же, как и у рекуррентности. Мы звоним $r_{1},\ldots ,r_{n}$ характерные корни рецидива. Если последовательность состоит из целых или рациональных чисел, корнями будут алгебраические числа .Если $d$ корни $r_{1},r_{2},\dots ,r_{d}$ все различны, то полиномы $k_{i}(n)$ все являются константами, которые можно определить из начальных значений последовательности.Если корни характеристического многочлена не различны и $r_{i}$ является корнем множественности $m$, затем $k_{i}(n)$ в формуле имеет степень $m-1$. Например, если характеристические полиномиальные коэффициенты как $(x-r)^{3}$, где один и тот же корень r встречается трижды, то $n$й термин имеет форму $s_{n}=(a+bn+cn^{2})r^{n}.$

Свойства замыкания

Примеры

Сумма двух константно-рекурсивных последовательностей также является константно-рекурсивной. Например, сумма $s_{n}=2^{n}$ и $t_{n}=n$ является $u_{n}=2^{n}+n$ ( $1,3,6,11,20,\ldots$), что удовлетворяет рекуррентности $u_{n}=4u_{n-1}-5u_{n-2}+2u_{n-3}$. Новую рекуррентность можно найти, сложив производящие функции для каждой последовательности.

Аналогично, произведение двух константно-рекурсивных последовательностей является константно-рекурсивным. Например, продукт $s_{n}=2^{n}$ и $t_{n}=n$ является $u_{n}=n\cdot 2^{n}$ ( $0,2,8,24,64,\ldots$), что удовлетворяет рекуррентности $u_{n}=4u_{n-1}-4u_{n-2}$.

Последовательность сдвига влево $u_{n}=s_{n+1}$ и последовательность сдвига вправо $u_{n}=s_{n-1}$ (с $u_{0}=0$) являются константно-рекурсивными, поскольку удовлетворяют одному и тому же рекуррентному соотношению. Например, потому что $s_{n}=2^{n}$ является константно-рекурсивным, поэтому $u_{n}=2^{n+1}$.

Список операций

В общем случае константно-рекурсивные последовательности замыкаются при следующих операциях, где $s=(s_{n})_{n\in \mathbb {N} },t=(t_{n})_{n\in \mathbb {N} }$ обозначают константно-рекурсивные последовательности, $f(x),g(x)$ являются их производящими функциями, а $d,e$ их заказы соответственно.

Операции над константно-рекурсивными последовательностями

Операция	Определение	Требование	Эквивалент производящей функции	Заказ
Сумма по срокам $s+t$	$(s+t)_{n}=s_{n}+t_{n}$	—	$f(x)+g(x)$	$\leq d+e$
Срок годности продукта $s\cdot t$	$(s\cdot t)_{n}=s_{n}\cdot t_{n}$	—	${\frac {1}{2\pi i}}\int _{\gamma }{\frac {f(\zeta )}{\zeta }}g\left({\frac {x}{\zeta }}\right)\;\mathrm {d} \zeta$	$\leq d\cdot e$
Продукт Коши $s*t$	$(s*t)_{n}=\sum _{i=0}^{n}s_{i}t_{n-i}$	—	$f(x)g(x)$	$\leq d+e$
Левый сдвиг $Ls$	$(Ls)_{n}=s_{n+1}$	—	${\frac {f(x)-s_{0}}{x}}$	$\leq d$
Правый сдвиг $Rs$	$(Rs)_{n}={\begin{cases}s_{n-1}&n\geq 1\\0&n=0\end{cases}}$	—	$xf(x)$	$\leq d+1$
Коши обратный $s^{(-1)}$	$(s^{(-1)})_{n}=\sum _{{i_{1}+\dots +i_{k}=n} \atop {i_{1},\ldots ,i_{k}\neq 0}}(-1)^{k}s_{i_{1}}s_{i_{2}}\cdots s_{i_{k}}$	$s_{0}=1$	${\frac {1}{f(x)}}$	$\leq d+1$
Клини звезда $s^{(*)}$	$(s^{(*)})_{n}=\sum _{{i_{1}+\dots +i_{k}=n} \atop {i_{1},\ldots ,i_{k}\neq 0}}s_{i_{1}}s_{i_{2}}\cdots s_{i_{k}}$	$s_{0}=0$	${\frac {1}{1-f(x)}}$	$\leq d+1$

Замыкание при почленном сложении и умножении следует из характеризации замкнутой формы в терминах экспоненциальных полиномов. Замыкание по произведению Коши следует из характеристики производящей функции. Требование $s_{0}=1$ обратное для Коши необходимо для случая целочисленных последовательностей, но его можно заменить на $s_{0}\neq 0$ если последовательность находится в любом поле (рациональных, алгебраических, действительных или комплексных числах).

Поведение

Основные статьи: теорема Сколема – Малера – Леха и проблема Сколема.

Нерешенная задача по математике :

Существует ли алгоритм проверки того, имеет ли константно-рекурсивная последовательность ноль?

(еще нерешенные задачи по математике)

Нули

Несмотря на то, что константно-рекурсивная последовательность удовлетворяет простой локальной формуле, она может демонстрировать сложное глобальное поведение. Определите ноль константно-рекурсивной последовательности как неотрицательное целое число. $n$ такой, что $s_{n}=0$. Теорема Скулема–Малера–Леха утверждает, что нули последовательности со временем повторяются: существуют константы $M$ и $N$ такой, что для всех $n>M$, $s_{n}=0$ тогда и только тогда, когда $s_{n+N}=0$. Этот результат справедлив для константно-рекурсивной последовательности над комплексными числами или, в более общем смысле, над любым полем характеристики нулевой .

Проблемы с решением

Структура нулей в константно-рекурсивной последовательности также может быть исследована с точки зрения теории вычислимости . Для этого описание последовательности $s_{n}$ должно быть дано конечное описание ; это можно сделать, если последовательность состоит из целых или рациональных чисел или даже над алгебраическими числами. При такой кодировке последовательностей $s_{n}$, можно изучить следующие проблемы:

Известные проблемы с решением

Проблема	Описание	Статус
Существование нуля ( задача Сколема )	На входе $(s_{n})_{n=0}^{\infty }$, является $s_{n}=0$ для некоторых $n$?	Открыть
Бесконечно много нулей	На входе $(s_{n})_{n=0}^{\infty }$, является $s_{n}=0$ для бесконечно многих $n$?	разрешимый
В итоге все ноль	На входе $(s_{n})_{n=0}^{\infty }$, является $s_{n}=0$ для всех достаточно больших $n$?	разрешимый
Позитивность	На входе $(s_{n})_{n=0}^{\infty }$, является $s_{n}>0$ для всех $n$?	Открыть
Возможная позитивность	На входе $(s_{n})_{n=0}^{\infty }$, является $s_{n}>0$ для всех достаточно больших $n$?	Открыть

Поскольку квадрат константно-рекурсивной последовательности $s_{n}^{2}$ по-прежнему является константно-рекурсивным (см. свойства замыкания ), проблема существования нуля в таблице выше сводится к положительности, а проблема «бесконечно много нулей» сводится к возможной положительности. К приведенным в таблице выше сводятся и другие проблемы: например, $s_{n}=c$ для некоторых $n$ сводится к существованию нуля для последовательности $s_{n}-c$. В качестве второго примера, для последовательностей действительных чисел слабая положительность (т. $s_{n}\geq 0$ для всех $n$?) сводится к положительности последовательности $-s_{n}$ (поскольку ответ должен быть отрицательным, это сокращение Тьюринга ).

Теорема Скулема-Малера-Леха могла бы дать ответы на некоторые из этих вопросов, за исключением того, что ее доказательство неконструктивно . В нем говорится, что для всех $n>M$, нули повторяются; однако ценность $M$ не известно, что вычислимо, поэтому это не приводит к решению проблемы существования нуля. С другой стороны, точная картина, которая повторяется после $n>M$ является вычислимым. Вот почему проблема бесконечного множества нулей разрешима: просто определите, является ли бесконечно повторяющийся шаблон пустым.

Результаты разрешимости известны, когда порядок последовательности ограничен малым. Например, проблема Скулема разрешима для алгебраических последовательностей порядка до 3 и вещественных алгебраических последовательностей до порядка 4. Также известно, что оно разрешимо для обратимых целочисленных последовательностей до порядка 7, то есть последовательностей, которые можно продолжать в обратном направлении в целых числах.

Известны также результаты о разрешимости в предположении некоторых недоказанных гипотез теории чисел . Например, разрешимость известна для рациональных последовательностей порядка до 5 с учетом гипотезы Скулема (также известной как экспоненциальный локально-глобальный принцип). Разрешимость также известна для всех простых рациональных последовательностей (с простым характеристическим полиномом), подчиняющихся гипотезе Скулема и слабой p-адической гипотезе Шануэля .

Вырождение

Позволять $r_{1},\ldots ,r_{n}$ — характеристические корни постоянной рекурсивной последовательности $s$. Будем говорить, что последовательность вырождена, если какое-либо отношение $r_{i}/r_{j}$ является корнем единства, ибо $i\neq j$. Невырожденные последовательности зачастую легче изучать, в определенном смысле к этому можно свести, используя следующую теорему: если $s$ имеет порядок $d$ и содержится в числовом поле $K$ степени $k$ над $\mathbb {Q}$, то существует константа $M(k,d)\leq {\begin{cases}\exp(2d(3\log d)^{1/2})&{\text{if }}k=1,\\2^{kd+1}&{\text{if }}k\geq 2\end{cases}}$

такое, что для некоторых $M\leq M(k,d)$ каждая подпоследовательность $s_{Mn+\ell }$ либо тождественно равен нулю, либо невырожден.

Обобщения

D -конечная или голономная последовательность — это естественное обобщение, в котором коэффициенты рекуррентности могут быть полиномиальными функциями от $n$ а не константы.

А $k$-регулярная последовательность удовлетворяет линейным рекуррентам с постоянными коэффициентами, но рекурренты принимают другую форму. Скорее, чем $s_{n}$ представляет собой линейную комбинацию $s_{m}$ для некоторых целых чисел $m$ которые близки к $n$, каждый термин $s_{n}$ в $k$-регулярная последовательность представляет собой линейную комбинацию $s_{m}$ для некоторых целых чисел $m$ чья база - $k$ представления близки к $n$. Постоянно-рекурсивные последовательности можно рассматривать как $1$-регулярные последовательности, где основанию 1 представление по $n$ состоит из $n$ копии цифры $1$.

Ссылки

• Бруссо, Альфред (1971). Линейная рекурсия и последовательности Фибоначчи . Ассоциация Фибоначчи.
• Кауэрс, Мануэль; Пол, Питер (2010). Конкретный тетраэдр: символические суммы, рекуррентные уравнения, производящие функции, асимптотические оценки . Спрингер Вена. п. 66. ИСБН  978-3-7091-0444-6 .
• Стэнли, Ричард П. (2011). Перечислительная комбинаторика (PDF) . Том. 1 (2-е изд.). Кембриджские исследования в области высшей математики.

Внешние ссылки

• «Индекс OEIS Rec» . Индекс OEIS для нескольких тысяч примеров линейных повторений, отсортированных по порядку (количеству терминов) и сигнатуре (вектору значений постоянных коэффициентов)