Аксонометрия

Кавалерийский выступ полукруглой арки.

Аксонометрия — графическая процедура, относящаяся к начертательной геометрии , создающая планарное изображение трехмерного объекта. Термин «аксонометрия» означает «измерение по осям » и указывает на то, что размеры и масштаб координатных осей играют решающую роль. Результатом аксонометрической процедуры является параллельная проекция объекта в равномерном масштабе. В общем случае результирующая параллельная проекция является косой (лучи не перпендикулярны плоскости изображения); но в особых случаях результат ортогональный (лучи перпендикулярны плоскости изображения), что в данном контексте называется ортогональной аксонометрией .

В техническом рисовании и архитектуре аксонометрическая перспектива — это форма двухмерного изображения трехмерных объектов, цель которой — сохранить впечатление объема или рельефа . Иногда ее еще называют быстрой перспективой или искусственной перспективой. Она отличается от конической перспективы и не отражает то, что на самом деле видит глаз: в частности, параллельные линии остаются параллельными, а удаленные объекты не уменьшаются в размерах. Его можно рассматривать как коническую перспективу, центр которой выдвинут на бесконечность, то есть очень далеко от наблюдаемого объекта.

Термин аксонометрия используется как для описанной ниже графической процедуры, так и для изображения, полученного с помощью этой процедуры.

Аксонометрию не следует путать с аксонометрической проекцией , которая в англоязычной литературе обычно относится к ортогональной аксонометрии .

Принцип аксонометрии

Суть ${\overline {P}}$ это проекция точки $P=(x,y,z)$ на плоскость проекции Π . Ракурсы $v_{x}$, $v_{y}$ и $v_{z}$.

Теорема Польке лежит в основе следующей процедуры построения масштабированной параллельной проекции трехмерного объекта:

1. Выбирайте проекции осей координат так, чтобы все три оси координат не сводились в одну точку или линию. Обычно ось Z вертикальна.
2. Подберите для этих проекций ракурсы , $v_{x}$, $v_{y}$ и $v_{z}$, где $v_{x},v_{y},v_{z}>0.$
3. Проекция ${\overline {P}}$ точки $P=(x,y,z)$ определяется в три подэтапа (результат не зависит от порядка этих подэтапов):
   • начиная с точки ${\overline {O}}$, переместиться на сумму $v_{x}\cdot x$ в направлении ${\overline {x}}$, затем
   • двигаться на сумму $v_{y}\cdot y$ в направлении ${\overline {y}}$, затем
   • двигаться на сумму $v_{z}\cdot z$ в направлении ${\overline {z}}$ и наконец
4. Отметьте конечное положение как точку ${\overline {P}}$.

Чтобы получить неискаженные результаты, тщательно подбирайте проекции осей и ракурсы (см. ниже). Для создания ортогональной проекции свободно выбираются только проекции координатных осей; ракурсы фиксированы (см. de:orthogonale Axonometerie ).

Выбор изображений осей и ракурсов

Параметры и обозначения

Обозначение:

• $\alpha :$ угол между ${\overline {z}}$-ось и ${\overline {x}}$-ось
• $\beta :$ угол между ${\overline {z}}$-ось и ${\overline {y}}$-ось
• $\gamma :$ угол между ${\overline {x}}$-ось и ${\overline {y}}$-ось.

Углы чтобы можно выбрать так, $0^{\circ }<\alpha +\beta <360^{\circ }\ .$
Ракурсы ​ : $0<\;v_{x},\;v_{y},\;v_{z}\ .$

Только при правильном выборе ракурсов и ракурсов можно получить неискаженные изображения. Следующая диаграмма показывает изображения единичного куба под разными углами и ракурсами и дает несколько советов о том, как сделать этот личный выбор.

Различные аксонометрические изображения единичного куба. (Плоскость изображения параллельна плоскости yz.)
Левое и крайнее правое изображения больше похожи на удлиненные кубоиды, а не на куб.

Аксонометрия (бесцеремонная перспектива) дома на клетчатой ​​выкройке.

Чтобы рисунок был простым, следует выбирать простые ракурсы, например $1.0$ или $0.5$.

Если два ракурса равны, проекцию называют диметрической .
Если три ракурса равны, проекцию называют изометрической .
Если все ракурсы различны, проекция называется триметрической .

Параметры на диаграмме справа (например, дома, нарисованного на миллиметровой бумаге): $\alpha =135^{\circ },\beta =90^{\circ },\ v_{y}=v_{z}=1,\;v_{x}=1/{\sqrt {2}}\ .$ Следовательно, это диметрическая аксонометрия. Плоскость изображения параллельна плоскости yz, и любая плоская фигура, параллельная плоскости yz, появляется в своей истинной форме.

Специальная аксонометрия

от горизонта (α _h , β _h , без γ _h = 90°) и коэффициентами масштабирования ( vi _{Часто используемые проекции и перспективы с углами между преобразованными осями координат (α, β, γ), углами} )

Имя или свойство	α = ∠ x̄z̄	β = ∠ ş̄	γ = ∠ x̄ş	α ч	β ч	в х	v y	в я	v
Ортогональный, орфографический, плоский	90°	0°	270°	0°	270°	v		0%	любой
Триметрический	90° + α ч	90° + β ч	360° − а − б	любой	любой	любой	любой	любой	любой
Диметрический							v
Изометрический						v
Нормальный									100%
Косой, клинографический				< 90°	< 90°	любой	любой	любой	загар(α час )
Симметричный		а	360° − 2·а	< 90°	α ч				любой
равноугольный	120°			30°
Нормальный, 1:1 изометрический						v			100%
Стандартный, укороченный изометрический									${\textstyle {\sqrt {\frac {2}{3}}}}$ ≈ 81%
Пиксель, изометрия 1:2	116.6°		126.9°	арктан( v )					50%
Инженерное дело	131.4°	97.2°	131.4°	арккос( ⁠ 3 / 4 ⁠ )	арксисин( ⁠ 1 / 8 ⁠ )	50%	v		100%
Кавалер	90° + α ч	90°	270° − а	любой	0°	любой
Шкаф, диметрический кавалер						< 100 %
Стандартный, изометрический кавалер	135°		135°	45°		v
Стандартный шкаф 1:2						50%	v
шкаф 30°	116.6°		153.4°	арктан( v x )
шкаф 60°	153.4°		116.6°	дуговой кот ( v x )
30° кавалер	120°		150°	30°		любой
Аэрофотоснимок, вид с высоты птичьего полета	135°		90°	45°		v		любой	100%
Военный						v
Планометрический	90° + α ч	180° − α ч		любой	90° − α ч				любой
Нормальный планометрический									100%
Укороченный планометрический									⁠ 2 / 3 ⁠ ≈ 67%

Параметры специальной аксонометрии.

Инженерный прогноз

В этом случае

• ракурсы такие : $v_{x}=0.5,\ v_{y}=v_{z}=1\$ (диметрическая аксонометрия) и
• углы между осями равны: $\alpha =132^{\circ },\ \beta =97^{\circ }\ .$

Эти углы отмечены на многих немецких угольниках .

Преимущества инженерной проекции:

• простые ракурсы,
• ортогональная проекция с единым масштабом и масштабным коэффициентом 1,06,
• контур сферы — круг (вообще, эллипс).

Для получения более подробной информации: см. de:Axonometerie .

Кавалеристская перспектива, перспектива кабинета

• Плоскость изображения параллельна плоскости yz.

В литературе термины «кавалерская перспектива» и «кабинетская перспектива» не имеют единого определения. Приведенное выше определение является наиболее общим. Часто применяются дополнительные ограничения. Например:

перспектива шкафа: дополнительно выберите $\alpha =135^{\circ }$ (косой) и $v_{x}=0.5$ (диметрический),

бесцеремонный взгляд: дополнительно выберите $\alpha =135^{\circ }$ (косой) и $v_{x}=1$ (изометрический).

Вид с высоты птичьего полета, военная проекция

• Плоскость изображения параллельна плоскости xy.

военная проекция: дополнительно выберите $v_{z}=1$ (изометрический).

Такая аксонометрия часто используется для карт городов, чтобы сохранить неискаженные горизонтальные фигуры.

Изометрическая аксонометрия

стандартная изометрия: куб, кубоид, дом и сфера

(Не путать с изометрией метрических пространств.)

Для изометрической аксонометрии все ракурсы равны. Углы могут быть выбраны произвольно, но обычно выбирают $\alpha =\beta =\gamma =120^{\circ }$.

Для стандартной изометрии или просто изометрии можно выбрать:

• $v_{x}=v_{y}=v_{z}=1$ (все оси неискажены)
• $\alpha =\beta =\gamma =120^{\circ }\ .$

Преимущество стандартной изометрии:

• координаты можно взять неизменными,
• изображение представляет собой масштабированную ортогональную проекцию с масштабным коэффициентом ${\sqrt {1.5}}=1.225$. Следовательно, изображение производит хорошее впечатление, а контур сферы представляет собой круг.
• Некоторые компьютерные графические системы (например, xfig ) предоставляют в качестве поддержки подходящий растр (см. диаграмму).

Чтобы предотвратить масштабирование, можно выбрать неудобные ракурсы.

• $v_{x}=v_{y}=v_{z}={\sqrt {2/3}}$ (вместо 1)

и изображение представляет собой (немасштабированную) ортогональную проекцию.

различные аксонометрии башни
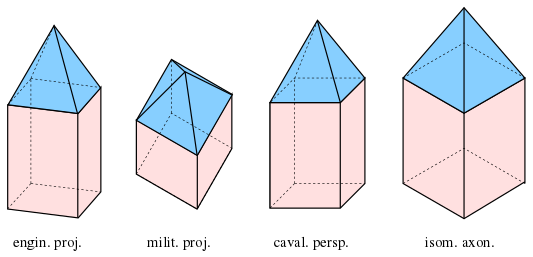
диметрическая военная проекция: $v_{z}=0.5,v_{x,y}=1$, диметрическая инженерия и бесцеремонные проекции: $v_{x}=0.5,v_{y,z}=1$, изометрическая аксонометрия: $v_{x,y,z}=1$

Круги в аксонометрии

Параллельная проекция окружности, вообще говоря, представляет собой эллипс. Возникает важный частный случай, если плоскость круга параллельна плоскости изображения: тогда изображение круга является конгруэнтным кругом. На диаграмме круг, содержащийся на лицевой грани, не искажен. Если изображение круга представляет собой эллипс, можно сопоставить четыре точки с ортогональными диаметрами и окружающим квадратом касательных, а в параллелограмме изображения заполнить эллипс вручную. Более лучший, но более трудоемкий метод состоит в рисовании изображений двух перпендикулярных диаметров круга, являющихся сопряженными диаметрами изображения эллипса, определении осей эллипса с помощью конструкции Ритца и рисовании эллипса .

• 
  Кавалерийская перспектива: круги
• 
  Военная проекция: сфера

Сферы в аксонометрии

В общей аксонометрии сферы контур изображения представляет собой эллипс. Контур сферы представляет собой круг только в ортогональной аксонометрии. Но поскольку инженерная проекция и стандартная изометрия представляют собой масштабированные ортогональные проекции, контур сферы и в этих случаях представляет собой круг. Как показано на диаграмме, эллипс как контур сферы может сбить с толку, поэтому, если сфера является частью объекта, который нужно нанести на карту, следует выбрать ортогональную аксонометрию, инженерную проекцию или стандартную изометрию.

Ссылки

• Граф, Ульрих; Барнер, Мартин (1961). Начертательная геометрия . Гейдельберг: Квелле и Мейер. ISBN  3-494-00488-9 .
• Фуке, Кирх Никель (1998). Начертательная геометрия . Лейпциг: специализированное книжное издательство. ISBN  3-446-00778-4 .
• Леопольд, Корнели (2005). Геометрические основы архитектурного изображения . Штутгарт: Кольхаммер Верлаг . ISBN  3-17-018489-Х .
• Браилов Александр Юрьевич (2016). Инженерная графика: теоретические основы инженерной геометрии для проектирования . Спрингер. ISBN  978-3-319-29717-0 .
• Старк, Роланд (1978). Начертательная геометрия . Шёнинг. ISBN  3-506-37443-5 .

Примечания

Внешние ссылки

• Ортогональная аксонометрия