Постоянная Планка

Приведенная постоянная Планка
Приведенная постоянная Планка
Общие символы
И объединились	джоуль-секунда
Другие подразделения	электронвольт-секунда
В базовых единицах СИ	kg ⋅ m 2 ⋅ s −1
Выводы из ; другие количества	;
Измерение
Ценить	1.054 571 817 ... × 10 −34 J⋅s ; 6.582 119 569 ... × 10 −16 eV⋅s

Постоянная Планка
Постоянная Планка
Общие символы
И объединились	Джоуль на герц (джоуль-секунда)
Другие подразделения	электронвольт на герц (электронвольт-секунда)
В базовых единицах СИ	kg ⋅ m 2 ⋅ s −1
Измерение
Ценить	6.626 070 15 × 10 −34 J⋅Hz −1 ; 4.135 667 696 ... × 10 −15 eV⋅Hz −1

, Постоянная Планка или постоянная Планка , обозначаемая ${\textstyle h}$ , ^[1] фундаментальная физическая константа ^[1] имеет основополагающее значение в квантовой механике : энергия фотона равна его частоте, умноженной на постоянную Планка, а длина равна волны материи постоянной Планка, разделенной на импульс соответствующей частицы.

Константа была постулирована Максом Планком в 1900 году как константа пропорциональности, необходимая для объяснения экспериментального излучения черного тела . ^[2] Позднее Планк назвал эту константу «квантом действия ». ^[3] В 1905 году Альберт Эйнштейн связал «квант» или минимальный элемент энергии с самой электромагнитной волной. Макс Планк получил Нобелевскую премию по физике 1918 года «в знак признания заслуг, которые он оказал развитию физики открытием квантов энергии».

В метрологии постоянная Планка используется вместе с другими константами для определения килограмма , единицы СИ . массы ^[4] Единицы СИ определены таким образом, что, когда постоянная Планка выражается в единицах СИ, она имеет точное значение $h$ = 6.626 070 15 × 10 ⁻³⁴ J⋅Hz ⁻¹. ‍ ^[5]^[6]

История

Происхождение константы

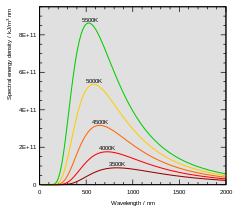
Постоянная Планка была сформулирована как часть успешной попытки Макса Планка создать математическое выражение, которое точно предсказывало бы наблюдаемое спектральное распределение теплового излучения закрытой печи ( излучение черного тела ). ^[7] Это математическое выражение теперь известно как закон Планка.

В последние годы XIX века Макс Планк исследовал проблему излучения черного тела, впервые поставленную Кирхгофом примерно 40 лет назад. Каждое физическое тело самопроизвольно и непрерывно излучает электромагнитное излучение . Не было никакого выражения или объяснения общей формы наблюдаемого спектра излучения. В то время закон Вина соответствовал данным для коротких волн и высоких температур, но не подходил для длинных волн. ^[7]^: 141 Примерно в это же время, но без ведома Планка, лорд Рэлей теоретически вывел формулу, теперь известную как закон Рэлея-Джинса , которая могла разумно предсказывать длинные волны, но потерпела полную неудачу на коротких длинах волн.

Подходя к этой проблеме, Планк предположил, что уравнения движения света описывают набор гармонических осцилляторов , по одному на каждую возможную частоту. Он исследовал, как энтропия осцилляторов меняется в зависимости от температуры тела, пытаясь соответствовать закону Вина, и смог вывести приблизительную математическую функцию для спектра черного тела: ^[2] что дало простую эмпирическую формулу для длинных волн.

Планк пытался найти математическое выражение, которое могло бы воспроизвести закон Вина (для коротких волн) и эмпирическую формулу (для длинных волн). Это выражение включало константу, $h$ , который, как предполагается, относится к Hilfsgrösse (вспомогательная переменная), ^[8] и впоследствии стала известна как постоянная Планка. Выражение, сформулированное Планком, показало, что спектральная яркость тела для частоты $ν$ при абсолютной температуре $T$ определяется выражением

B_{\nu }(\nu ,T)={\frac {2h\nu ^{3}}{c^{2}}}{\frac {1}{e^{\frac {h\nu }{k_{\mathrm {B} }T}}-1}}

,

где $k_{\text{B}}$ — постоянная Больцмана , $h$ – постоянная Планка, а $c$ это скорость света в среде, будь то материал или вакуум. ^[9]^[10]^[11]

Спектральное сияние тела, $B_{\nu }$ , описывает количество энергии, которую он излучает на разных частотах излучения. Это мощность, излучаемая на единицу площади тела, на единицу телесного угла излучения, на единицу частоты. Спектральную яркость также можно выразить на единицу длины волны. $\lambda$ вместо на единицу частоты. В данном случае оно определяется

B_{\lambda }(\lambda ,T)={\frac {2hc^{2}}{\lambda ^{5}}}{\frac {1}{e^{\frac {hc}{\lambda k_{\mathrm {B} }T}}-1}}

,

показывая, как излучаемая энергия, излучаемая на более коротких волнах, увеличивается с температурой быстрее, чем энергия, излучаемая на более длинных волнах. ^[12]

Закон Планка также можно выразить в других терминах, например, в количестве фотонов, испускаемых на определенной длине волны, или в плотности энергии в объеме излучения. Единица СИ $B_{\nu }$ это Вт · ср ⁻¹· м ⁻²· Гц ⁻¹, в то время как $B_{\lambda }$ W ·ср ⁻¹·м ⁻³.

Планк вскоре понял, что его решение не уникально. Было несколько разных решений, каждое из которых давало разное значение энтропии осцилляторов. ^[2] Чтобы спасти свою теорию, Планк прибегнул к использованию спорной в то время теории статистической механики . ^[2] который он назвал «актом отчаяния». ^[13] Одним из его новых граничных условий было

интерпретировать U _N [ колебательную энергию N осцилляторов ] не как непрерывную, бесконечно делимую величину, а как дискретную величину, состоящую из целого числа конечных равных частей. Назовем каждую такую часть элементом энергии ε ;
- Планк, О законе распределения энергии в нормальном спектре. ^[2]

При этом новом условии Планк наложил квантование энергии осцилляторов, «чисто формальное предположение… на самом деле я особо об этом не задумывался…» по его собственным словам: ^[14] но тот, который произвел бы революцию в физике. Применение этого нового подхода к закону смещения Вина показало, что «элемент энергии» должен быть пропорционален частоте осциллятора, что является первой версией того, что сейчас иногда называют « соотношением Планка-Эйнштейна »:

E=hf.

Планк смог вычислить величину $h$ из экспериментальных данных по излучению черного тела: его результат 6,55 × 10 ⁻³⁴ Дж⋅с находится в пределах 1,2% от текущего определенного значения. ^[2] Он также впервые определил постоянную Больцмана. $k_{\text{B}}$ на основе тех же данных и теории. ^[15]

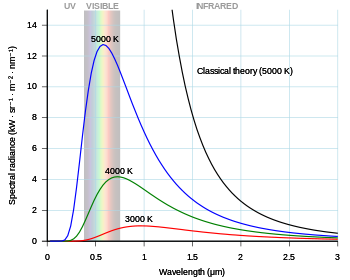
Разработка и применение

К проблеме черного тела вновь обратились в 1905 году, когда лорд Рэлей , Джеймс Джинс (вместе) и Альберт Эйнштейн независимо друг от друга доказали, что классический электромагнетизм никогда не сможет объяснить наблюдаемый спектр. Эти доказательства широко известны как « ультрафиолетовая катастрофа » — название, придуманное Паулем Эренфестом в 1911 году. Они внесли большой вклад (наряду с работами Эйнштейна по фотоэлектрическому эффекту ) в убеждение физиков в том, что постулат Планка о квантованных уровнях энергии был чем-то большим, чем просто математическим утверждением. формализм. Первая Сольвеевская конференция 1911 г. была посвящена «теории излучения и квантов». ^[16]

Фотоэлектрический эффект

Фотоэлектрический эффект — это эмиссия электронов (так называемых «фотоэлектронов») с поверхности при освещении ее светом. Впервые его наблюдал Александр Эдмон Беккерель в 1839 году, хотя обычно заслуга принадлежит Генриху Герцу . ^[17] который опубликовал первое тщательное исследование в 1887 году. Другое особенно тщательное исследование было опубликовано Филиппом Ленардом (Ленар Фюлёп) в 1902 году. ^[18] Статья Эйнштейна 1905 года ^[19] обсуждение этого эффекта с точки зрения квантов света принесло бы ему Нобелевскую премию в 1921 году. ^[17] после того, как его предсказания были подтверждены экспериментальной работой Роберта Эндрюса Милликена . ^[20] Нобелевский комитет присудил премию за работу по фотоэлектрическому эффекту, а не за теорию относительности, как из-за предвзятого отношения к чисто теоретической физике, не основанной на открытиях или экспериментах, так и из-за разногласий среди его членов относительно фактического доказательства реальности теории относительности. . ^[21]^[22]

До появления статьи Эйнштейна считалось, что электромагнитное излучение, такое как видимый свет, ведет себя как волна: отсюда и использование терминов «частота» и «длина волны» для характеристики различных типов излучения. Энергия, передаваемая волной за данное время, называется ее интенсивностью . Свет театрального прожектора более яркий , чем свет домашней лампочки; то есть прожектор выделяет больше энергии в единицу времени и на единицу пространства (и, следовательно, потребляет больше электроэнергии), чем обычная лампочка, даже если цвет света может быть очень похожим. Другие волны, такие как звуковые волны или волны, разбивающиеся о береговую линию, также имеют свою интенсивность. Однако энергетический учет фотоэлектрического эффекта, похоже, не согласовывался с волновым описанием света.

«Фотоэлектроны», испускаемые в результате фотоэффекта, обладают определенной кинетической энергией , которую можно измерить. Эта кинетическая энергия (для каждого фотоэлектрона) не зависит от интенсивности света. ^[18] но зависит линейно от частоты; ^[20] и если частота слишком низкая (соответствует энергии фотонов, которая меньше работы выхода материала), фотоэлектроны вообще не испускаются, за исключением множества фотонов, энергетическая сумма которых больше, чем энергия фотоэлектронов, действует практически одновременно (многофотонный эффект). ^[23] Предполагая, что частота достаточно высока, чтобы вызвать фотоэлектрический эффект, увеличение интенсивности источника света приводит к испусканию большего количества фотоэлектронов с той же кинетической энергией, а не к испусканию того же количества фотоэлектронов с более высокой кинетической энергией. ^[18]

Объяснение Эйнштейном этих наблюдений заключалось в том, что свет сам по себе квантуется; что энергия света не передается непрерывно, как в классической волне, а только небольшими «пакетами» или квантами. Размер этих «пакетов» энергии, которые позже будут названы фотонами , должен был быть таким же, как «энергетический элемент» Планка, что дает современную версию соотношения Планка-Эйнштейна:

E=hf.

Позднее экспериментально был доказан постулат Эйнштейна: константа пропорциональности между частотой падающего света $f$ и кинетическая энергия фотоэлектронов $E$ было показано, что он равен постоянной Планка $h$ . ^[20]

Атомная структура

В 1912 году Джон Уильям Николсон разработал ^[24] атомную модель и обнаружил, что угловые моменты электронов в модели связаны соотношением h /2 $π$ . ^[25]^[26] Ядерная квантовая атомная модель Николсона повлияла на развитие Нильса Бора . атомной модели ^[27]^[28]^[26] и Бор процитировал его в своей статье 1913 года о модели атома Бора. ^[29]Модель Бора вышла за рамки абстрактной концепции гармонического осциллятора Планка: электрон в атоме Бора мог иметь только определенные определенные энергии. $E_{n}$

E_{n}=-{\frac {hcR_{\infty }}{n^{2}}},

где $c$ скорость света в вакууме, $R_{\infty }$ — экспериментально определенная константа ( константа Ридберга ) и $n\in \{1,2,3,...\}$ . Этот подход также позволил Бору объяснить формулу Ридберга , эмпирическое описание атомного спектра водорода, и объяснить значение константы Ридберга. $R_{\infty }$ в терминах других фундаментальных констант.При обсуждении углового момента электронов в своей модели Бор ввел величину ${\frac {h}{2\pi }}$ , теперь известная как приведенная постоянная Планка как квант углового момента . ^[29]

Принцип неопределенности

Постоянная Планка также встречается в формулировках принципа неопределенности Вернера Гейзенберга . Учитывая многочисленные частицы, приготовленные в одном и том же состоянии, неопределенность в их положении $\Delta x$ и неопределенность в их импульсе, $\Delta p_{x}$ , подчиняться

\Delta x\,\Delta p_{x}\geq {\frac {\hbar }{2}},

где неопределенность выражается как стандартное отклонение измеренного значения от его ожидаемого значения . Есть еще несколько таких пар физически измеримых сопряженных переменных , которые подчиняются аналогичному правилу. Одним из примеров является время и энергия. Обратная зависимость между неопределенностью двух сопряженных переменных приводит к компромиссу в квантовых экспериментах, поскольку более точное измерение одной величины приводит к тому, что другая становится неточной.

В дополнение к некоторым предположениям, лежащим в основе интерпретации определенных значений в квантово-механической формулировке, один из фундаментальных краеугольных камней всей теории лежит в коммутаторном соотношении между оператором положения ${\hat {x}}$ и оператор импульса ${\hat {p}}$ :

[{\hat {p}}_{i},{\hat {x}}_{j}]=-i\hbar \delta _{ij},

где $\delta _{ij}$ это дельта Кронекера .

Фотонная энергия

Соотношение Планка связывает конкретную энергию фотона $E$ с соответствующей волновой частотой $f$ :

E=hf.

Эта энергия чрезвычайно мала по сравнению с обычно воспринимаемыми повседневными объектами.

Поскольку частота $f$ , длина волны $λ$ и скорость света $c$ связаны соотношением $f={\frac {c}{\lambda }}$ , отношение также можно выразить как

E={\frac {hc}{\lambda }}.

длина волны де Бройля

В 1923 году Луи де Бройль обобщил соотношение Планка-Эйнштейна, постулировав, что постоянная Планка представляет собой пропорциональность между импульсом и квантовой длиной волны не только фотона, но и квантовой длины волны любой частицы. Вскоре это было подтверждено экспериментами. Это справедливо для всей квантовой теории, включая электродинамику . Длина волны де Бройля $λ$ частицы определяется выражением

\lambda ={\frac {h}{p}},

где $p$ обозначает линейный импульс частицы, например фотона или любой другой элементарной частицы .

Энергия фотона с угловой частотой $ω = 2 πf$ определяется выражением

E=\hbar \omega ,

в то время как его линейный импульс относится к

p=\hbar k,

где $k$ — угловое волновое число .

Эти два отношения являются временной и пространственной частями специального релятивистского выражения с использованием 4-векторов .

P^{\mu }=\left({\frac {E}{c}},{\vec {p}}\right)=\hbar K^{\mu }=\hbar \left({\frac {\omega }{c}},{\vec {k}}\right).

Статистическая механика

Классическая статистическая механика требует существования $h$ (но не определяет его значение). ^[30] В конце концов, после открытия Планка, было высказано предположение, что физическое действие не может принимать произвольное значение, а вместо этого ограничивается целыми числами, кратными очень малой величине, «[элементарному] кванту действия», который теперь называется постоянной Планка . ^[31] Это была значительная концептуальная часть так называемой « старой квантовой теории », разработанной физиками, включая Бора , Зоммерфельда и Ишивары , в которой траектории частиц существуют, но скрыты , но квантовые законы ограничивают их на основе их действия. На смену этой точке зрения пришла вполне современная квантовая теория, в которой даже не существует определенных траекторий движения; скорее, частица представлена волновой функцией, распространенной в пространстве и во времени. ^[32]^: 373С этим связана концепция квантования энергии, которая существовала в старой квантовой теории, а также существует в измененной форме в современной квантовой физике. Классическая физика не может объяснить квантование энергии.

Размер и значение

Постоянная Планка имеет те же размерности , что и действие и угловой момент . В единицах СИ постоянная Планка выражается в единицах джоулей на герц (Дж⋅Гц ⁻¹) или джоуль-секунда (Дж⋅с).

h

= 6.626 070 15 × 10 ⁻³⁴ J⋅Hz ⁻¹‍ ^[5]

\hbar ={h \over 2\pi }

= 1.054 571 817 ... × 10 ⁻³⁴ J⋅s ‍ ^[33] = 6.582 119 569 ... × 10 ⁻¹⁶ eV⋅s . ^[34]

Вышеуказанные значения были приняты как фиксированные в переопределении базовых единиц СИ в 2019 году .

С 2019 года числовое значение постоянной Планка фиксировано и имеет конечное десятичное представление. Это фиксированное значение используется для определения единицы массы СИ, килограмма : «килограмм [...] определяется путем принятия фиксированного числового значения $h$ равного 6,626 070 15 × 10. ⁻³⁴ если выразить в единице Дж⋅с, что равно кг⋅м ²⋅s ⁻¹, где метр и секунда определяются через скорость света $c$ и длительность сверхтонкого перехода основного состояния невозмущенного цезия-133 атома $Δ ν Cs$ ». ^[35] Технологии массовой метрологии, такие как мера баланса Киббла , уточняют значение килограмма, применяя фиксированное значение постоянной Планка.

Значение значения

Константа Планка — одна из наименьших констант, используемых в физике. Это отражает тот факт, что в масштабе, адаптированном для людей, где энергия типична порядка килоджоулей, а время типично порядка секунд или минут, постоянная Планка очень мала. Когда произведение энергии и времени физического события приближается к постоянной Планка, доминируют квантовые эффекты. ^[36]

Аналогичным образом, порядок постоянной Планка отражает тот факт, что повседневные объекты и системы состоят из большого количества микроскопических частиц. Например, в зеленом свете (с длиной волны 555 нанометров или частотой 540 ТГц ) каждый фотон имеет энергию E = hf = 3,58 × 10 ⁻¹⁹ Дж . Это очень небольшое количество энергии с точки зрения повседневного опыта, но повседневный опыт касается отдельных фотонов не больше, чем отдельных атомов или молекул. Количество света, более типичное для повседневного опыта (хотя и гораздо большее, чем наименьшее количество света, воспринимаемое человеческим глазом), равно энергии одного моля фотонов; его энергию можно вычислить, умножив энергию фотона на постоянную Авогадро , N _A = 6,022 140 76 × 10 ²³ моль ⁻¹‍ ^[37], с результатом 216 кДж , о пищевой энергии в трёх яблоках. ^{[ нужна ссылка ]}

Приведенная постоянная Планка

Во многих приложениях квантовой физики величина, называемая приведенной постоянной Планка и равная ${\textstyle h/(2\pi )}$ появляется; это обозначается ${\textstyle \hbar }$ (произносится как х-бар ^[38]^{: 336}). ^[39]^[40]^{: 482}

Многие из наиболее важных уравнений, соотношений, определений и результатов квантовой механики обычно записываются с использованием приведенной постоянной Планка. ${\textstyle \hbar }$ а не постоянная Планка ${\textstyle h}$ , включая уравнение Шрёдингера , оператор импульса , каноническое коммутационное соотношение , принцип неопределённости Гейзенберга и единицы Планка . ^[41]^{: 104}

Фундаментальные уравнения выглядят проще, если записать их с помощью ${\textstyle \hbar }$ в отличие от ${\textstyle h}$ , и это обычно ${\textstyle \hbar }$ скорее, чем ${\textstyle h}$ это дает наиболее надежные результаты при использовании оценок порядка величины .Например, используя анализ размерностей для оценки энергии ионизации атома водорода, соответствующие параметры, определяющие энергию ионизации, ${\textstyle E_{\text{i}}}$ масса электрона ${\textstyle m_{\text{e}}}$ , заряд электрона ${\textstyle e}$ , и либо постоянная Планка ${\textstyle h}$ или приведенная постоянная Планка ${\textstyle \hbar }$ : $E_{\text{i}}\propto m_{\text{e}}e^{4}/h^{2}\ {\text{or}}\ \propto m_{\text{e}}e^{4}/\hbar ^{2}$ Поскольку обе константы имеют одинаковые размерности, они войдут в анализ размерностей одинаково, но с ${\textstyle \hbar }$ оценка находится в пределах двух раз, тогда как при ${\textstyle h}$ ошибка ближе к ${\textstyle (2\pi )^{2}\approx 40}$ . ^[42]^: 8–9

Имена и символы

Приведенная постоянная Планка известна под многими другими названиями: приведенная постоянная Планка. ^[43]^{: 5} ^[44]^{: 788}), рационализированная постоянная Планка ^[45]^{: 726}^[46]^{: 10}^[47]^{: -} (или рационализировать постоянную Планка ^[48]^{: 334} ^[49]^{: IX} , ^[50]^{: 112} Дирака постоянная ^[51]^{: 275} ^[45]^{: 726} ^[52]^{: хв} (или постоянная Дирака ^[53]^{: 148} ^[54]^{: 604} ^[55]^{: 313}), Дирак ${\textstyle h}$ ^[56]^[57]^{: восемнадцатый} (или Дирака ${\textstyle h}$ ^[58]^{: 17} ), Дирак ${\textstyle \hbar }$ ^[59]^{: 187} (или Дирака ${\textstyle \hbar }$ ^[60]^{: 273} ^[61]^{: 14} ) и h-бар . ^[62]^{: 558}^[63]^{: 561} Об этом также часто упоминают ${\textstyle \hbar }$ как «постоянная Планка» ^[64]^{: 55} ^[а] сохраняя при этом отношения ${\textstyle \hbar =h/(2\pi )}$ .

На сегодняшний день наиболее распространенным обозначением приведенной постоянной Планка является ${\textstyle \hbar }$ . Однако в некоторых источниках это обозначается как ${\textstyle h}$ вместо этого, и в этом случае они обычно называют его «Диракским ${\textstyle h}$ " ^[90]^{: 43} ^[91]^{: 151} (или «Дирака ${\textstyle h}$ " ^[92]^{: 21}).

История

Комбинация ${\textstyle h/(2\pi )}$ появилось в статье Нильса Бора 1913 года. ^[93]^{: 15} где это обозначалось ${\textstyle M_{0}}$ . ^[26]^: 169^[б] В течение следующих 15 лет эта комбинация продолжала появляться в литературе, но обычно без отдельного символа. ^[94]^{: 180}^[с] Затем, в 1926 году, в своих основополагающих статьях Шредингер и Дирак снова ввели для него специальные символы: ${\textstyle K}$ в случае со Шрёдингером, ^[106] и ${\textstyle h}$ в случае Дирака. ^[107] Дирак продолжал использовать ${\textstyle h}$ таким образом до 1930 г. ^[108]^{: 291} когда он ввел символ ${\textstyle \hbar }$ в своей книге «Принципы квантовой механики» . ^[108]^{: 291} ^[109]

См. также

Примечания

^ Яркие примеры такого использования включают Ландау и Лифшица. ^[65]^{: 20} и Гриффитс , ^[66]^{: 3} но есть много других, например ^[67]^[68]^: 449 ^[69]^{: 284} ^[70]^{: 3} ^[71]^{: 365} ^[72]^{: 14} ^[73]^{: 18} ^[74]^{: 4} ^[75]^{: 138} ^[76]^{: 251} ^[77]^{: 1} ^[78]^{: 622} ^[79]^{: хх} ^[80]^{: 20} ^[81]^{: 4} ^[82]^{: 36} ^[83]^{: 41} ^[84]^{: 199} ^[85]^: 846 ^[86]^[87]^[88]^: 25 ^[89]^: 653
^ Бор обозначается ${\textstyle M}$ угловой момент электрона вокруг ядра и записал условие квантования как ${\textstyle M=\tau M_{0}}$ , где ${\textstyle \tau }$ является положительным целым числом. (См. модель Бора .)
^ Вот некоторые статьи, упомянутые в ^[94] и в котором ${\textstyle h/(2\pi )}$ появилось без отдельного символа: ^[95]^: 428 ^[96]^{: 549} ^[97]^{: 508} ^[98]^{: 230} ^[99]^: 458 ^[100]^[101]^{: 276} ^[102]^[103]^[104]. ^[105]

Ссылки

Цитаты

^ Перейти обратно: ^а ^б «Постоянная Планка» . Справочник NIST по константам, единицам измерения и неопределенности . НИСТ . 20 мая 2019 г. Архивировано из оригинала 27 мая 2022 г. Проверено 03 сентября 2023 г.
^ Перейти обратно: ^а ^б ^с ^д ^и ^ж Планк, Макс (1901), «О законе распределения энергии в нормальном спектре» (PDF) , Ann. Физ. , 309 (3): 553–63, Bibcode : 1901AnP...309..553P , doi : 10.1002/andp.19013090310 , заархивировано (PDF) из оригинала 10 июня 2012 г. , получено 15 декабря 2008 г. Английский перевод: «О законе распределения энергии в нормальном спектре» . Архивировано из оригинала 18 апреля 2008 г. ". «О законе распределения энергии в нормальном спектре» (PDF) . Архивировано из оригинала (PDF) 6 октября 2011 г. Проверено 13 октября 2011 г.
^ «Нобелевская лекция Макса Планка» . Архивировано из оригинала 14 июля 2023 г. Проверено 14 июля 2023 г.
^ Международная система единиц (PDF) (9-е изд.), Международное бюро мер и весов, декабрь 2022 г., стр. 131, ISBN 978-92-822-2272-0
^ Перейти обратно: ^а ^б «Значение CODATA 2022: постоянная Планка» . Справочник NIST по константам, единицам измерения и неопределенности . НИСТ . Май 2024 года . Проверено 18 мая 2024 г.
^ «Резолюции 26-й ГКМВ» (PDF) . БИПМ . 16.11.2018. Архивировано из оригинала (PDF) 19 ноября 2018 г. Проверено 20 ноября 2018 г.
^ Перейти обратно: ^а ^б Биттер, Фрэнсис ; Medicus, Генрих А. (1973). Поля и частицы . Нью-Йорк: Эльзевир. стр. 137–144.
^ Бойя, Луис Дж. (2004). «Формула теплового излучения Планка (1900 г.)». arXiv : физика/0402064v1 .
^ Планк, М. (1914). Теория теплового излучения . Масиус, М. (перевод) (2-е изд.). Сын П. Блэкистона. С. 6, 168. ОЛ 7154661М .
^ Чандрасекхар, С. (1960) [1950]. Перенос излучения (пересмотренное переиздание). Дувр . п. 8. ISBN 978-0-486-60590-6 .
^ Рыбицкий, ГБ; Лайтман, AP (1979). Радиационные процессы в астрофизике . Уайли . п. 22. ISBN 978-0-471-82759-7 . Архивировано из оригинала 27 июля 2020 г. Проверено 20 мая 2020 г.
^ Шао, Гаофэн; и др. (2019). «Повышение стойкости к окислению высокоэмиссионных покрытий на волокнистой керамике для многоразовых космических систем». Коррозионная наука . 146 : 233–246. arXiv : 1902.03943 . Бибкод : 2019Corro.146..233S . дои : 10.1016/j.corsci.2018.11.006 . S2CID 118927116 .
^ Краг, Хельге (1 декабря 2000 г.), Макс Планк: сопротивляющийся революционер , PhysicsWorld.com, заархивировано из оригинала 8 января 2009 г.
^ Краг, Хельге (1999), Квантовые поколения: история физики в двадцатом веке , Princeton University Press, стр. 62, ISBN 978-0-691-09552-3 , заархивировано из оригинала 06 декабря 2021 г. , получено 31 октября 2021 г.
^ Планк, Макс (2 июня 1920 г.), «Происхождение и современное состояние развития квантовой теории» (Нобелевская лекция) , заархивировано из оригинала 15 июля 2011 г. , получено 13 декабря 2008 г.
^ Предыдущие конференции Solvay по физике , Международные институты Solvay, заархивировано из оригинала 16 декабря 2008 г. , получено 12 декабря 2008 г.
^ Перейти обратно: ^а ^б См., например, Аррениус, Сванте (10 декабря 1922 г.), речь на вручении Нобелевской премии по физике 1921 г. , заархивировано из оригинала 4 сентября 2011 г. , получено 13 декабря 2008 г.
^ Перейти обратно: ^а ^б ^с Ленард, П. (1902), «О фотоэлектрическом эффекте» , Annals of Physics , 313 (5): 149–98, Бибкод : 1902AnP...313..149L , doi : 10.1002/andp.19023130510 , заархивировано из оригинал 18 августа 2019 г. , получено 3 июля 2019 г.
^ Эйнштейн, Альберт (1905), «Об эвристической точке зрения на производство и преобразование света» (PDF) , Annals of Physics , 17 (6): 132–48, Бибкод : 1905AnP...322..132E , doi : 10.1002/andp.19053220607 , заархивировано (PDF) из оригинала 9 июля 2011 г. , получено 3 декабря 2009 г.
^ Перейти обратно: ^а ^б ^с Милликен, Р.А. Планка (1916), «Прямое фотоэлектрическое определение h », Physical Review , 7 (3): 355–88, Бибкод : 1916PhRv....7..355M , doi : 10.1103/PhysRev.7.355
^ Исааксон, Уолтер (10 апреля 2007 г.), Эйнштейн: его жизнь и вселенная , Саймон и Шустер, ISBN 978-1-4165-3932-2 , заархивировано из оригинала 09 января 2020 г. , получено 31 октября 2021 г. , стр. 309–314.
^ «Нобелевская премия по физике 1921 года» . Нобелевская премия.org. Архивировано из оригинала 3 июля 2018 г. Проверено 23 апреля 2014 г.
^
* Смит, Ричард (1962). «Двухфотонный фотоэлектрический эффект». Физический обзор . 128 (5): 2225. Бибкод : 1962PhRv..128.2225S . дои : 10.1103/PhysRev.128.2225 .
- Смит, Ричард (1963). «Двухфотонный фотоэффект» . Физический обзор . 130 (6): 2599. Бибкод : 1963PhRv..130.2599S . дои : 10.1103/PhysRev.130.2599.4 .
^
- Николсон, JW (1912). «Конституция солнечной короны II» . Ежемесячные уведомления Королевского астрономического общества . 72 (8): 677–693. дои : 10.1093/mnras/72.8.677 .
^ Хейлброн, Джон Л. (2013). «Путь к квантовому атому». Природа . 498 (7452): 27–30. дои : 10.1038/498027a . ПМИД 23739408 . S2CID 4355108 .
^ Перейти обратно: ^а ^б ^с МакКорммах, Рассел (1966). «Атомная теория Джона Уильяма Николсона». Архив истории точных наук . 3 (2): 160–184. дои : 10.1007/BF00357268 . JSTOR 41133258 . S2CID 120797894 .
^ Хиросигэ, Тету; Нисио, Сигеко (1964). «Формирование теории атомного строения Бора». Японские исследования в истории науки . 3 :6–28.
^ Дж. Л. Хейлброн, История атомных моделей от открытия электрона до истоков квантовой механики, дисс. (Калифорнийский университет, Беркли, 1964 г.).
^ Перейти обратно: ^а ^б Бор, Н. (1913). «О строении атомов и молекул» . Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 6-я серия. 26 (151): 1–25. Бибкод : 1913PMag...26..476B . дои : 10.1080/14786441308634955 . Архивировано из оригинала 07 марта 2023 г. Проверено 23 июля 2023 г.
^ Джузеппе Моранди; Ф. Неаполь; Э. Эрколесси (2001), Статистическая механика: промежуточный курс , World Scientific, с. 84, ISBN 978-981-02-4477-4 , заархивировано из оригинала 06 декабря 2021 г. , получено 31 октября 2021 г.
^ тер Хаар, Д. (1967). Старая квантовая теория . Пергамон Пресс. п. 133 . ISBN 978-0-08-012101-7 .
^ Эйнштейн, Альберт (2003), «Физика и реальность» (PDF) , Дедал , 132 (4): 24, doi : 10.1162/001152603771338742 , S2CID 57559543 , заархивировано из оригинала (PDF) 15 апреля 2012 г., Вопрос Первый вопрос: как можно приписать дискретную последовательность значений энергии $H σ$ системе, заданной в смысле классической механики (функция энергии есть заданная функция координат $q r$ и соответствующих импульсов $p r$ )? Постоянная Планка $h$ связывает частоту $H σ / h$ со значениями энергии $H σ$ . Поэтому достаточно придать системе последовательность дискретных значений частоты.
^ «Значение CODATA 2022: приведенная постоянная Планка» . Справочник NIST по константам, единицам измерения и неопределенности . НИСТ . Май 2024 года . Проверено 18 мая 2024 г.
^ «Значение CODATA: приведенная постоянная Планка в эВ·с» . физика.nist.gov .
^ Международная система единиц (PDF) (9-е изд.), Международное бюро мер и весов, декабрь 2022 г., ISBN 978-92-822-2272-0
^ «Лекции Фейнмана по физике, том II, глава 19: Принцип наименьшего действия» . www.feynmanlectures.caltech.edu . Проверено 3 ноября 2023 г.
^ «Значение CODATA 2022: константа Авогадро» . Справочник NIST по константам, единицам измерения и неопределенности . НИСТ . Май 2024 года . Проверено 18 мая 2024 г.
^ Чабай, Рут В .; Шервуд, Брюс А. (20 ноября 2017 г.). Материя и взаимодействия . Джон Уайли и сыновья. ISBN 978-1-119-45575-2 .
^ «приведенная постоянная Планка» . Справочник NIST по константам, единицам измерения и неопределенности . НИСТ . 20 мая 2019 г. Архивировано из оригинала 8 апреля 2023 г. Проверено 03 сентября 2023 г.
^ Лит, Дэвид Х .; Лиддл, Эндрю Р. (11 июня 2009 г.). Первичное возмущение плотности: космология, инфляция и происхождение структуры . Издательство Кембриджского университета. ISBN 978-1-139-64374-0 .
^ Шварц, Патрисия М.; Шварц, Джон Х. (25 марта 2004 г.). Специальная теория относительности: от Эйнштейна к струнам . Издательство Кембриджского университета. ISBN 978-1-139-44950-2 .
^ Леви-Леблон, Жан-Марк (2002). «Значения постоянной Планка» (PDF) . В Бельтраметти, Э.; Римини, А.; Роботти, Надя (ред.). Сто лет H: Павия, 14–16 сентября 2000 г. Итальянское физическое общество. ISBN 978-88-7438-003-9 . Архивировано из оригинала (PDF) 14 октября 2023 г.
^ Хуанг, Керсон (26 апреля 2010 г.). Квантовая теория поля: от операторов к интегралам по траекториям . Джон Уайли и сыновья. ISBN 978-3-527-40846-7 .
^ Шмитц, Кеннет С. (11 ноября 2016 г.). Физическая химия: понятия и теория . Эльзевир. ISBN 978-0-12-800600-9 .
^ Перейти обратно: ^а ^б Ренни, Ричард; Ло, Джонатан, ред. (2017). «Постоянная Планка» . Словарь физики . Оксфордский краткий справочник (7-е изд.). Оксфорд, Великобритания: ОУП Оксфорд. ISBN 978-0198821472 .
^ Международная энциклопедия физической химии и химической физики . Пергамон Пресс. 1960.
^ Вертес, Аттила; Надь, Шандор; Кленчар, Золтан; Ловас, Дьёрдь Резсо; Рёш, Франк (10 декабря 2010 г.). Справочник по ядерной химии . Springer Science & Business Media. ISBN 978-1-4419-0719-6 .
^ Бете, Ганс А .; Солпитер, Эдвин Э. (1957). «Квантовая механика одно- и двухэлектронных атомов». Во Флюгге, Зигфрид (ред.). Handbuch der Physik: Атом I-II . Спрингер.
^ Ланг, Кеннет (11 ноября 2013 г.). Астрофизические формулы: сборник для физиков и астрофизиков . Springer Science & Business Media. ISBN 978-3-662-11188-8 .
^ Гальгани, Л.; Карати, А.; Поцци, Б. (декабрь 2002 г.). «Проблема скорости термализации и связь между классической и квантовой механикой». В Фабрицио, Мауро; Морро, Анджело (ред.). Математические модели и методы для интеллектуальных материалов, Кортона, Италия, 25–29 июня 2001 г. стр. 111–122. дои : 10.1142/9789812776273_0011 . ISBN 978-981-238-235-1 .
^ Фокс, Марк (14 июня 2018 г.). Руководство для студентов по атомной физике . Издательство Кембриджского университета. ISBN 978-1-316-99309-5 .
^ Кляйсс, Рональд (10 июня 2021 г.). Квантовая теория поля: диаграммный подход . Издательство Кембриджского университета. ISBN 978-1-108-78750-5 .
^ Зохури, Бахман (5 января 2021 г.). Тепловое воздействие мощной лазерной энергии на материалы . Спрингер Природа. ISBN 978-3-030-63064-5 .
^ Балиан, Роджер (26 июня 2007 г.). От микрофизики к макрофизике: методы и приложения статистической физики. Том II . Springer Science & Business Media. ISBN 978-3-540-45480-9 .
^ Чен, К. Джулиан (15 августа 2011 г.). Физика солнечной энергии . Джон Уайли и сыновья. ISBN 978-1-118-04459-9 .
^ «Дирак ч » . Британника . Архивировано из оригинала 17 февраля 2023 г. Проверено 27 сентября 2023 г.
^ Шенберг, Д. (3 сентября 2009 г.). Магнитные колебания в металлах . Издательство Кембриджского университета. ISBN 978-1-316-58317-3 .
^ Пауэлл, Джон Л.; Краземанн, Бернд (5 мая 2015 г.). Квантовая механика . Публикации Courier Dover. ISBN 978-0-486-80478-1 .
^ Дрезден, Макс (6 декабря 2012 г.). Х.А. Крамерс Между традицией и революцией . Springer Science & Business Media. ISBN 978-1-4612-4622-0 .
^ Джонсон, RE (6 декабря 2012 г.). Введение в атомные и молекулярные столкновения . Springer Science & Business Media. ISBN 978-1-4684-8448-9 .
^ Гарсия, Алехандро; Хенли, Эрнест М. (13 июля 2007 г.). Субатомная физика (3-е изд.). Мировое научное издательство. ISBN 978-981-310-167-8 .
^ Холброу, Чарльз Х .; Ллойд, Джеймс Н.; Амато, Джозеф К.; Гальвез, Энрике; Паркс, М. Элизабет (14 сентября 2010 г.). Современная вводная физика . Нью-Йорк: Springer Science & Business Media. ISBN 978-0-387-79080-0 .
^ Полянин Андрей Дмитриевич ; Черноуцан, Алексей (18 октября 2010 г.). Краткий справочник по математике, физике и инженерным наукам . ЦРК Пресс. ISBN 978-1-4398-0640-1 .
^ Даулинг, Джонатан П. (24 августа 2020 г.). Сеть Шрёдингера: гонка за создание квантового Интернета . ЦРК Пресс. ISBN 978-1-000-08017-9 .
^ Ландау, LD ; Лифшиц, Э.М. (22 октября 2013 г.). Квантовая механика: нерелятивистская теория . Эльзевир. ISBN 978-1-4831-4912-7 .
^ Гриффитс, Дэвид Дж .; Шретер, Даррелл Ф. (20 ноября 2019 г.). Введение в квантовую механику . Издательство Кембриджского университета. ISBN 978-1-108-10314-5 .
^ «Постоянная Планка» . Большая советская энциклопедия (1970–1979, 3-е изд.). Группа Гейл.
^ Ицыксон, Клод ; Зубер, Жан-Бернар (20 сентября 2012 г.). Квантовая теория поля . Курьерская компания. ISBN 978-0-486-13469-7 .
^ Каку, Мичио (1993). Квантовая теория поля: современное введение . Издательство Оксфордского университета. ISBN 978-0-19-507652-3 .
^ Боголюбов Николай Николаевич ; Ширков Дмитрий Васильевич (1982). Квантовые поля . Бенджамин / Издательская компания Каммингс, Продвинутая книжная программа / Отдел мировой науки. ISBN 978-0-8053-0983-6 .
^ Эйчисон, Ян-младший ; Привет, Энтони Дж.Г. (17 декабря 2012 г.). Калибровочные теории в физике элементарных частиц: практическое введение: от релятивистской квантовой механики к КЭД, четвертое издание . ЦРК Пресс. ISBN 978-1-4665-1299-3 .
^ де Вит, Б .; Смит, Дж. (2 декабря 2012 г.). Теория поля в физике элементарных частиц, Том 1 . Эльзевир. ISBN 978-0-444-59622-2 .
^ Браун, Лоуэлл С. (1992). Квантовая теория поля . Издательство Кембриджского университета. ISBN 978-0-521-46946-3 .
^ Бухбиндер, Иосиф Л.; Шапиро, Илья (март 2021 г.). Введение в квантовую теорию поля с приложениями к квантовой гравитации . Издательство Оксфордского университета. ISBN 978-0-19-883831-9 .
^ Яффе, Артур (25 марта 2004 г.). «9. Какое место в общей картине занимает квантовая теория поля?». В Цао, Тянь Юй (ред.). Концептуальные основы квантовой теории поля . Издательство Кембриджского университета. ISBN 978-0-521-60272-3 .
^ Кабиббо, Никола ; Майани, Лучано ; Бенхар, Омар (28 июля 2017 г.). Введение в калибровочные теории . ЦРК Пресс. ISBN 978-1-4987-3452-3 .
^ Казальбуони, Роберто (6 апреля 2017 г.). Введение в квантовую теорию поля (второе изд.). Мировое научное издательство. ISBN 978-981-314-668-6 .
^ Дас, Ашок (24 июля 2020 г.). Лекции по квантовой теории поля (2-е изд.). Всемирная научная. ISBN 978-981-12-2088-3 .
^ Десаи, Бипин Р. (2010). Квантовая механика с базовой теорией поля . Издательство Кембриджского университета. ISBN 978-0-521-87760-2 .
^ Донохью, Джон; Сорбо, Лоренцо (8 марта 2022 г.). Прелюдия к квантовой теории поля . Издательство Принстонского университета. ISBN 978-0-691-22348-3 .
^ Фолланд, Джеральд Б. (3 февраля 2021 г.). Квантовая теория поля: Туристический путеводитель для математиков . Американское математическое соц. ISBN 978-1-4704-6483-7 .
^ Фрадкин, Эдуардо (23 марта 2021 г.). Квантовая теория поля: комплексный подход . Издательство Принстонского университета. ISBN 978-0-691-14908-0 .
^ Желис, Франсуа (11 июля 2019 г.). Квантовая теория поля . Издательство Кембриджского университета. ISBN 978-1-108-48090-1 .
^ Грейнер, Уолтер ; Рейнхардт, Иоахим (9 марта 2013 г.). Квантовая электродинамика . Springer Science & Business Media. ISBN 978-3-662-05246-4 .
^ Либофф, Ричард Л. (2003). Вводная квантовая механика (4-е изд.). Сан-Франциско: Pearson Education. ISBN 978-81-317-0441-7 .
^ Барут, АО (1 августа 1978 г.). «Создание фотона: эвристический расчет постоянной Планка ħ или постоянной тонкой структуры α» . Zeitschrift für Naturforschung A. 33 (8): 993–994. Бибкод : 1978ЗНатА..33..993Б . дои : 10.1515/zna-1978-0819 . S2CID 45829793 .
^ Косия, Лукас; С любовью, Питер (12 июля 2018 г.). «Контекстуальность измерения и постоянная Планка». Новый журнал физики . 20 (7): 073020. arXiv : 1711.08066 . Бибкод : 2018NJPh...20g3020K . дои : 10.1088/1367-2630/aacef2 . S2CID 73623448 .
^ Хамферис, Дэвид (28 ноября 2022 г.). «Неявная структура постоянной Планка» . Европейский журнал прикладной физики . 4 (6): 22–25. doi : 10.24018/ejphysical.2022.4.6.227 . S2CID 254359279 .
^ Байс, Ф. Александр; Фармер, Дж. Дойн (2008). «Физика информации» . В Адриансе, Питер; ван Бентем, Йохан (ред.). Философия информации . Справочник по философии науки. Том. 8. Амстердам: Северная Голландия. arXiv : 0708.2837 . ISBN 978-0-444-51726-5 .
^ Хирота, Э.; Сакакима, Х.; Иномата, К. (9 марта 2013 г.). Гигантские устройства магнитосопротивления . Springer Science & Business Media. ISBN 978-3-662-04777-4 .
^ Гарднер, Джон Х. (1988). «Теория инвариантности». Энциклия . 65 : 139.
^ Левин, Рафаэль Д. (4 июня 2009 г.). Динамика молекулярных реакций . Издательство Кембриджского университета. ISBN 978-1-139-44287-9 .
^ Бор, Н. (июль 1913 г.). «I. О строении атомов и молекул» . Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 26 (151): 1–25. Бибкод : 1913PMag...26....1B . дои : 10.1080/14786441308634955 .
^ Перейти обратно: ^а ^б Мехра, Джагдиш ; Рехенберг, Гельмут (3 августа 1982 г.). Историческое развитие квантовой теории . Том. 1. Спрингер Нью-Йорк. ISBN 978-0-387-90642-3 .
^ Зоммерфельд, А. (1915). «К теории рядов Бальмера» (PDF) . Протоколы заседаний математического и физического класса КБ Академии наук в Мюнхене . 33 (198): 425–458. дои : 10.1140/epjh/e2013-40053-8 .
^ Шварцшильд, К. (1916). «О квантовой гипотезе». Труды Королевской прусской академии наук в Берлине : 548–568.
^ Эренфест, П. (июнь 1917 г.). «XLVIII. Адиабатические инварианты и теория квантов». Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 33 (198): 500–513. дои : 10.1080/14786440608635664 .
^ Ланде, А. (июнь 1919 г.). «Серийный спектр гелия». Физический журнал . 20 :228-234.
^ Бор, Н. (октябрь 1920 г.). «О рядовом спектре элементов». Журнал физики . 2 (5): 423–469. Бибкод : 1920ZPhy....2..423B . дои : 10.1007/BF01329978 .
^ Стерн, Отто (декабрь 1921 г.). «Путь к экспериментальной проверке направленного квантования в магнитном поле» . Журнал физики . 7 (1): 249–253. Бибкод : 1921ZPhy....7..249S . дои : 10.1007/BF01332793 .
^ Гейзенберг, Вернер (декабрь 1922 г.). «К квантовой теории линейной структуры и аномальным зеемановским отражениям». Журнал физики . 8 (1): 273–297. Бибкод : 1922ZPhy....8..273H . дои : 10.1007/BF01329602 .
^ Крамерс, Х.А. Паули, В. (декабрь 1923 г.). «К теории зонных спектров» . Журнал физики . 13 (1): 351–367. Бибкод : 1923ZPhy...13..351K . дои : 10.1007/BF01328226 .
^ Борн, М .; Джордан, П. (декабрь 1925 г.). «О квантовой механике». Журнал физики . 34 (1): 858–888. Бибкод : 1925ZPhy...34..858B . дои : 10.1007/BF01328531 .
^ Дирак, ПАМ (декабрь 1925 г.). «Основные уравнения квантовой механики» . Труды Лондонского королевского общества. Серия А, содержащая статьи математического и физического характера . 109 (752): 642–653. Бибкод : 1925RSPSA.109..642D . дои : 10.1098/rspa.1925.0150 .
^ Борн, М .; Гейзенберг, В .; Джордан, П. (август 1926 г.). «О квантовой механике. II». Журнал физики . 35 (8–9): 557–615. Бибкод : 1926ZPhy...35..557B . дои : 10.1007/BF01379806 .
^ Шрёдингер, Э. (1926). «Квантование как проблема собственных значений» . Анналы физики . 384 (4): 361–376. Бибкод : 1926АнП...384..361С . дои : 10.1002/andp.19263840404 .
^ Дирак, ПАМ (октябрь 1926 г.). «К теории квантовой механики» . Труды Лондонского королевского общества. Серия А, содержащая статьи математического и физического характера . 112 (762): 661–677. Бибкод : 1926RSPSA.112..661D . дои : 10.1098/rspa.1926.0133 .
^ Перейти обратно: ^а ^б Мехра, Джагдиш ; Рехенберг, Гельмут (2000). Историческое развитие квантовой теории . Том. 6. Нью-Йорк: Спрингер.
^ Дирак, ПАМ (1930). Принципы квантовой механики (1-е изд.). Оксфорд, Великобритания: Кларендон.

Источники

Барроу, Джон Д. (2002), Константы природы; От альфы до омеги - числа, которые кодируют глубочайшие тайны Вселенной , Pantheon Books, ISBN 978-0-375-42221-8

Внешние ссылки

[90] Яркие примеры такого использования включают Ландау и Лифшица. ^[65]^{: 20} и Гриффитс , ^[66]^{: 3} но есть много других, например ^[67]^[68]^: 449 ^[69]^{: 284} ^[70]^{: 3} ^[71]^{: 365} ^[72]^{: 14} ^[73]^{: 18} ^[74]^{: 4} ^[75]^{: 138} ^[76]^{: 251} ^[77]^{: 1} ^[78]^{: 622} ^[79]^{: хх} ^[80]^{: 20} ^[81]^{: 4} ^[82]^{: 36} ^[83]^{: 41} ^[84]^{: 199} ^[85]^: 846 ^[86]^[87]^[88]^: 25 ^[89]^: 653

[95] Бор обозначается ${\textstyle M}$ угловой момент электрона вокруг ядра и записал условие квантования как ${\textstyle M=\tau M_{0}}$ , где ${\textstyle \tau }$ является положительным целым числом. (См. модель Бора .)

[108] Вот некоторые статьи, упомянутые в ^[94] и в котором ${\textstyle h/(2\pi )}$ появилось без отдельного символа: ^[95]^: 428 ^[96]^{: 549} ^[97]^{: 508} ^[98]^{: 230} ^[99]^: 458 ^[100]^[101]^{: 276} ^[102]^[103]^[104]. ^[105]

[NIST_h-1] Перейти обратно: ^а ^б «Постоянная Планка» . Справочник NIST по константам, единицам измерения и неопределенности . НИСТ . 20 мая 2019 г. Архивировано из оригинала 27 мая 2022 г. Проверено 03 сентября 2023 г.

[Planck01-2] Перейти обратно: ^а ^б ^с ^д ^и ^ж Планк, Макс (1901), «О законе распределения энергии в нормальном спектре» (PDF) , Ann. Физ. , 309 (3): 553–63, Bibcode : 1901AnP...309..553P , doi : 10.1002/andp.19013090310 , заархивировано (PDF) из оригинала 10 июня 2012 г. , получено 15 декабря 2008 г. Английский перевод: «О законе распределения энергии в нормальном спектре» . Архивировано из оригинала 18 апреля 2008 г. ". «О законе распределения энергии в нормальном спектре» (PDF) . Архивировано из оригинала (PDF) 6 октября 2011 г. Проверено 13 октября 2011 г.

[3] «Нобелевская лекция Макса Планка» . Архивировано из оригинала 14 июля 2023 г. Проверено 14 июля 2023 г.

[4] Международная система единиц (PDF) (9-е изд.), Международное бюро мер и весов, декабрь 2022 г., стр. 131, ISBN 978-92-822-2272-0

[physconst-h-5] Перейти обратно: ^а ^б «Значение CODATA 2022: постоянная Планка» . Справочник NIST по константам, единицам измерения и неопределенности . НИСТ . Май 2024 года . Проверено 18 мая 2024 г.

[6] «Резолюции 26-й ГКМВ» (PDF) . БИПМ . 16.11.2018. Архивировано из оригинала (PDF) 19 ноября 2018 г. Проверено 20 ноября 2018 г.

[Bitter-7] Перейти обратно: ^а ^б Биттер, Фрэнсис ; Medicus, Генрих А. (1973). Поля и частицы . Нью-Йорк: Эльзевир. стр. 137–144.

[8] Бойя, Луис Дж. (2004). «Формула теплового излучения Планка (1900 г.)». arXiv : физика/0402064v1 .

[Planck_1914_6_168-9] Планк, М. (1914). Теория теплового излучения . Масиус, М. (перевод) (2-е изд.). Сын П. Блэкистона. С. 6, 168. ОЛ 7154661М .

[Chan8-10] Чандрасекхар, С. (1960) [1950]. Перенос излучения (пересмотренное переиздание). Дувр . п. 8. ISBN 978-0-486-60590-6 .

[Rybicki_1979_22-11] Рыбицкий, ГБ; Лайтман, AP (1979). Радиационные процессы в астрофизике . Уайли . п. 22. ISBN 978-0-471-82759-7 . Архивировано из оригинала 27 июля 2020 г. Проверено 20 мая 2020 г.

[12] Шао, Гаофэн; и др. (2019). «Повышение стойкости к окислению высокоэмиссионных покрытий на волокнистой керамике для многоразовых космических систем». Коррозионная наука . 146 : 233–246. arXiv : 1902.03943 . Бибкод : 2019Corro.146..233S . дои : 10.1016/j.corsci.2018.11.006 . S2CID 118927116 .

[Kragh-13] Краг, Хельге (1 декабря 2000 г.), Макс Планк: сопротивляющийся революционер , PhysicsWorld.com, заархивировано из оригинала 8 января 2009 г.

[14] Краг, Хельге (1999), Квантовые поколения: история физики в двадцатом веке , Princeton University Press, стр. 62, ISBN 978-0-691-09552-3 , заархивировано из оригинала 06 декабря 2021 г. , получено 31 октября 2021 г.

[PlanckNobel-15] Планк, Макс (2 июня 1920 г.), «Происхождение и современное состояние развития квантовой теории» (Нобелевская лекция) , заархивировано из оригинала 15 июля 2011 г. , получено 13 декабря 2008 г.

[16] Предыдущие конференции Solvay по физике , Международные институты Solvay, заархивировано из оригинала 16 декабря 2008 г. , получено 12 декабря 2008 г.

[Nobel21-17] Перейти обратно: ^а ^б См., например, Аррениус, Сванте (10 декабря 1922 г.), речь на вручении Нобелевской премии по физике 1921 г. , заархивировано из оригинала 4 сентября 2011 г. , получено 13 декабря 2008 г.

[Lenard-18] Перейти обратно: ^а ^б ^с Ленард, П. (1902), «О фотоэлектрическом эффекте» , Annals of Physics , 313 (5): 149–98, Бибкод : 1902AnP...313..149L , doi : 10.1002/andp.19023130510 , заархивировано из оригинал 18 августа 2019 г. , получено 3 июля 2019 г.

[19] Эйнштейн, Альберт (1905), «Об эвристической точке зрения на производство и преобразование света» (PDF) , Annals of Physics , 17 (6): 132–48, Бибкод : 1905AnP...322..132E , doi : 10.1002/andp.19053220607 , заархивировано (PDF) из оригинала 9 июля 2011 г. , получено 3 декабря 2009 г.

[Millikan-20] Перейти обратно: ^а ^б ^с Милликен, Р.А. Планка (1916), «Прямое фотоэлектрическое определение h », Physical Review , 7 (3): 355–88, Бибкод : 1916PhRv....7..355M , doi : 10.1103/PhysRev.7.355

[21] Исааксон, Уолтер (10 апреля 2007 г.), Эйнштейн: его жизнь и вселенная , Саймон и Шустер, ISBN 978-1-4165-3932-2 , заархивировано из оригинала 09 января 2020 г. , получено 31 октября 2021 г. , стр. 309–314.

[22] «Нобелевская премия по физике 1921 года» . Нобелевская премия.org. Архивировано из оригинала 3 июля 2018 г. Проверено 23 апреля 2014 г.

[23] * Смит, Ричард (1962). «Двухфотонный фотоэлектрический эффект». Физический обзор . 128 (5): 2225. Бибкод : 1962PhRv..128.2225S . дои : 10.1103/PhysRev.128.2225 .
Смит, Ричард (1963). «Двухфотонный фотоэффект» . Физический обзор . 130 (6): 2599. Бибкод : 1963PhRv..130.2599S . дои : 10.1103/PhysRev.130.2599.4 .

[27] Смит, Ричард (1963). «Двухфотонный фотоэффект» . Физический обзор . 130 (6): 2599. Бибкод : 1963PhRv..130.2599S . дои : 10.1103/PhysRev.130.2599.4 .

[24] 
Николсон, JW (1912). «Конституция солнечной короны II» . Ежемесячные уведомления Королевского астрономического общества . 72 (8): 677–693. дои : 10.1093/mnras/72.8.677 .

[29] Николсон, JW (1912). «Конституция солнечной короны II» . Ежемесячные уведомления Королевского астрономического общества . 72 (8): 677–693. дои : 10.1093/mnras/72.8.677 .

[HeilbronPath-25] Хейлброн, Джон Л. (2013). «Путь к квантовому атому». Природа . 498 (7452): 27–30. дои : 10.1038/498027a . ПМИД 23739408 . S2CID 4355108 .

[McCormmach-26] Перейти обратно: ^а ^б ^с МакКорммах, Рассел (1966). «Атомная теория Джона Уильяма Николсона». Архив истории точных наук . 3 (2): 160–184. дои : 10.1007/BF00357268 . JSTOR 41133258 . S2CID 120797894 .

[27] Хиросигэ, Тету; Нисио, Сигеко (1964). «Формирование теории атомного строения Бора». Японские исследования в истории науки . 3 :6–28.

[28] Дж. Л. Хейлброн, История атомных моделей от открытия электрона до истоков квантовой механики, дисс. (Калифорнийский университет, Беркли, 1964 г.).

[Bohr-29] Перейти обратно: ^а ^б Бор, Н. (1913). «О строении атомов и молекул» . Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 6-я серия. 26 (151): 1–25. Бибкод : 1913PMag...26..476B . дои : 10.1080/14786441308634955 . Архивировано из оригинала 07 марта 2023 г. Проверено 23 июля 2023 г.

[30] Джузеппе Моранди; Ф. Неаполь; Э. Эрколесси (2001), Статистическая механика: промежуточный курс , World Scientific, с. 84, ISBN 978-981-02-4477-4 , заархивировано из оригинала 06 декабря 2021 г. , получено 31 октября 2021 г.

[31] тер Хаар, Д. (1967). Старая квантовая теория . Пергамон Пресс. п. 133 . ISBN 978-0-08-012101-7 .

[32] Эйнштейн, Альберт (2003), «Физика и реальность» (PDF) , Дедал , 132 (4): 24, doi : 10.1162/001152603771338742 , S2CID 57559543 , заархивировано из оригинала (PDF) 15 апреля 2012 г., Вопрос Первый вопрос: как можно приписать дискретную последовательность значений энергии $H σ$ системе, заданной в смысле классической механики (функция энергии есть заданная функция координат $q r$ и соответствующих импульсов $p r$ )? Постоянная Планка $h$ связывает частоту $H σ / h$ со значениями энергии $H σ$ . Поэтому достаточно придать системе последовательность дискретных значений частоты.

[physconst-hbar-33] «Значение CODATA 2022: приведенная постоянная Планка» . Справочник NIST по константам, единицам измерения и неопределенности . НИСТ . Май 2024 года . Проверено 18 мая 2024 г.

[34] «Значение CODATA: приведенная постоянная Планка в эВ·с» . физика.nist.gov .

[35] Международная система единиц (PDF) (9-е изд.), Международное бюро мер и весов, декабрь 2022 г., ISBN 978-92-822-2272-0

[FeynmanII-36] «Лекции Фейнмана по физике, том II, глава 19: Принцип наименьшего действия» . www.feynmanlectures.caltech.edu . Проверено 3 ноября 2023 г.

[physconst-NA-37] «Значение CODATA 2022: константа Авогадро» . Справочник NIST по константам, единицам измерения и неопределенности . НИСТ . Май 2024 года . Проверено 18 мая 2024 г.

[Chabay_and_Sherwood-38] Чабай, Рут В .; Шервуд, Брюс А. (20 ноября 2017 г.). Материя и взаимодействия . Джон Уайли и сыновья. ISBN 978-1-119-45575-2 .

[NIST_reduced_h-39] «приведенная постоянная Планка» . Справочник NIST по константам, единицам измерения и неопределенности . НИСТ . 20 мая 2019 г. Архивировано из оригинала 8 апреля 2023 г. Проверено 03 сентября 2023 г.

[40] Лит, Дэвид Х .; Лиддл, Эндрю Р. (11 июня 2009 г.). Первичное возмущение плотности: космология, инфляция и происхождение структуры . Издательство Кембриджского университета. ISBN 978-1-139-64374-0 .

[41] Шварц, Патрисия М.; Шварц, Джон Х. (25 марта 2004 г.). Специальная теория относительности: от Эйнштейна к струнам . Издательство Кембриджского университета. ISBN 978-1-139-44950-2 .

[42] Леви-Леблон, Жан-Марк (2002). «Значения постоянной Планка» (PDF) . В Бельтраметти, Э.; Римини, А.; Роботти, Надя (ред.). Сто лет H: Павия, 14–16 сентября 2000 г. Итальянское физическое общество. ISBN 978-88-7438-003-9 . Архивировано из оригинала (PDF) 14 октября 2023 г.

[43] Хуанг, Керсон (26 апреля 2010 г.). Квантовая теория поля: от операторов к интегралам по траекториям . Джон Уайли и сыновья. ISBN 978-3-527-40846-7 .

[44] Шмитц, Кеннет С. (11 ноября 2016 г.). Физическая химия: понятия и теория . Эльзевир. ISBN 978-0-12-800600-9 .

[Oxford_Planck_constant-45] Перейти обратно: ^а ^б Ренни, Ричард; Ло, Джонатан, ред. (2017). «Постоянная Планка» . Словарь физики . Оксфордский краткий справочник (7-е изд.). Оксфорд, Великобритания: ОУП Оксфорд. ISBN 978-0198821472 .

[46] Международная энциклопедия физической химии и химической физики . Пергамон Пресс. 1960.

[47] Вертес, Аттила; Надь, Шандор; Кленчар, Золтан; Ловас, Дьёрдь Резсо; Рёш, Франк (10 декабря 2010 г.). Справочник по ядерной химии . Springer Science & Business Media. ISBN 978-1-4419-0719-6 .

[Bethe_and_Salpeter-48] Бете, Ганс А .; Солпитер, Эдвин Э. (1957). «Квантовая механика одно- и двухэлектронных атомов». Во Флюгге, Зигфрид (ред.). Handbuch der Physik: Атом I-II . Спрингер.

[49] Ланг, Кеннет (11 ноября 2013 г.). Астрофизические формулы: сборник для физиков и астрофизиков . Springer Science & Business Media. ISBN 978-3-662-11188-8 .

[50] Гальгани, Л.; Карати, А.; Поцци, Б. (декабрь 2002 г.). «Проблема скорости термализации и связь между классической и квантовой механикой». В Фабрицио, Мауро; Морро, Анджело (ред.). Математические модели и методы для интеллектуальных материалов, Кортона, Италия, 25–29 июня 2001 г. стр. 111–122. дои : 10.1142/9789812776273_0011 . ISBN 978-981-238-235-1 .

[Fox_Student_Guide_Atomic-51] Фокс, Марк (14 июня 2018 г.). Руководство для студентов по атомной физике . Издательство Кембриджского университета. ISBN 978-1-316-99309-5 .

[52] Кляйсс, Рональд (10 июня 2021 г.). Квантовая теория поля: диаграммный подход . Издательство Кембриджского университета. ISBN 978-1-108-78750-5 .

[53] Зохури, Бахман (5 января 2021 г.). Тепловое воздействие мощной лазерной энергии на материалы . Спрингер Природа. ISBN 978-3-030-63064-5 .

[54] Балиан, Роджер (26 июня 2007 г.). От микрофизики к макрофизике: методы и приложения статистической физики. Том II . Springer Science & Business Media. ISBN 978-3-540-45480-9 .

[55] Чен, К. Джулиан (15 августа 2011 г.). Физика солнечной энергии . Джон Уайли и сыновья. ISBN 978-1-118-04459-9 .

[56] «Дирак ч » . Британника . Архивировано из оригинала 17 февраля 2023 г. Проверено 27 сентября 2023 г.

[57] Шенберг, Д. (3 сентября 2009 г.). Магнитные колебания в металлах . Издательство Кембриджского университета. ISBN 978-1-316-58317-3 .

[58] Пауэлл, Джон Л.; Краземанн, Бернд (5 мая 2015 г.). Квантовая механика . Публикации Courier Dover. ISBN 978-0-486-80478-1 .

[59] Дрезден, Макс (6 декабря 2012 г.). Х.А. Крамерс Между традицией и революцией . Springer Science & Business Media. ISBN 978-1-4612-4622-0 .

[60] Джонсон, RE (6 декабря 2012 г.). Введение в атомные и молекулярные столкновения . Springer Science & Business Media. ISBN 978-1-4684-8448-9 .

[61] Гарсия, Алехандро; Хенли, Эрнест М. (13 июля 2007 г.). Субатомная физика (3-е изд.). Мировое научное издательство. ISBN 978-981-310-167-8 .

[Holbrow_et_al_Modern_Introductory_Physics-62] Холброу, Чарльз Х .; Ллойд, Джеймс Н.; Амато, Джозеф К.; Гальвез, Энрике; Паркс, М. Элизабет (14 сентября 2010 г.). Современная вводная физика . Нью-Йорк: Springer Science & Business Media. ISBN 978-0-387-79080-0 .

[63] Полянин Андрей Дмитриевич ; Черноуцан, Алексей (18 октября 2010 г.). Краткий справочник по математике, физике и инженерным наукам . ЦРК Пресс. ISBN 978-1-4398-0640-1 .

[64] Даулинг, Джонатан П. (24 августа 2020 г.). Сеть Шрёдингера: гонка за создание квантового Интернета . ЦРК Пресс. ISBN 978-1-000-08017-9 .

[Landau_and_Lifshit_Quantum_Mechanics-65] Ландау, LD ; Лифшиц, Э.М. (22 октября 2013 г.). Квантовая механика: нерелятивистская теория . Эльзевир. ISBN 978-1-4831-4912-7 .

[Griffiths_Quantum-66] Гриффитс, Дэвид Дж .; Шретер, Даррелл Ф. (20 ноября 2019 г.). Введение в квантовую механику . Издательство Кембриджского университета. ISBN 978-1-108-10314-5 .

[Soviet_Planck_constant-67] «Постоянная Планка» . Большая советская энциклопедия (1970–1979, 3-е изд.). Группа Гейл.

[68] Ицыксон, Клод ; Зубер, Жан-Бернар (20 сентября 2012 г.). Квантовая теория поля . Курьерская компания. ISBN 978-0-486-13469-7 .

[69] Каку, Мичио (1993). Квантовая теория поля: современное введение . Издательство Оксфордского университета. ISBN 978-0-19-507652-3 .

[70] Боголюбов Николай Николаевич ; Ширков Дмитрий Васильевич (1982). Квантовые поля . Бенджамин / Издательская компания Каммингс, Продвинутая книжная программа / Отдел мировой науки. ISBN 978-0-8053-0983-6 .

[71] Эйчисон, Ян-младший ; Привет, Энтони Дж.Г. (17 декабря 2012 г.). Калибровочные теории в физике элементарных частиц: практическое введение: от релятивистской квантовой механики к КЭД, четвертое издание . ЦРК Пресс. ISBN 978-1-4665-1299-3 .

[72] де Вит, Б .; Смит, Дж. (2 декабря 2012 г.). Теория поля в физике элементарных частиц, Том 1 . Эльзевир. ISBN 978-0-444-59622-2 .

[73] Браун, Лоуэлл С. (1992). Квантовая теория поля . Издательство Кембриджского университета. ISBN 978-0-521-46946-3 .

[74] Бухбиндер, Иосиф Л.; Шапиро, Илья (март 2021 г.). Введение в квантовую теорию поля с приложениями к квантовой гравитации . Издательство Оксфордского университета. ISBN 978-0-19-883831-9 .

[75] Яффе, Артур (25 марта 2004 г.). «9. Какое место в общей картине занимает квантовая теория поля?». В Цао, Тянь Юй (ред.). Концептуальные основы квантовой теории поля . Издательство Кембриджского университета. ISBN 978-0-521-60272-3 .

[76] Кабиббо, Никола ; Майани, Лучано ; Бенхар, Омар (28 июля 2017 г.). Введение в калибровочные теории . ЦРК Пресс. ISBN 978-1-4987-3452-3 .

[77] Казальбуони, Роберто (6 апреля 2017 г.). Введение в квантовую теорию поля (второе изд.). Мировое научное издательство. ISBN 978-981-314-668-6 .

[78] Дас, Ашок (24 июля 2020 г.). Лекции по квантовой теории поля (2-е изд.). Всемирная научная. ISBN 978-981-12-2088-3 .

[79] Десаи, Бипин Р. (2010). Квантовая механика с базовой теорией поля . Издательство Кембриджского университета. ISBN 978-0-521-87760-2 .

[80] Донохью, Джон; Сорбо, Лоренцо (8 марта 2022 г.). Прелюдия к квантовой теории поля . Издательство Принстонского университета. ISBN 978-0-691-22348-3 .

[81] Фолланд, Джеральд Б. (3 февраля 2021 г.). Квантовая теория поля: Туристический путеводитель для математиков . Американское математическое соц. ISBN 978-1-4704-6483-7 .

[82] Фрадкин, Эдуардо (23 марта 2021 г.). Квантовая теория поля: комплексный подход . Издательство Принстонского университета. ISBN 978-0-691-14908-0 .

[83] Желис, Франсуа (11 июля 2019 г.). Квантовая теория поля . Издательство Кембриджского университета. ISBN 978-1-108-48090-1 .

[84] Грейнер, Уолтер ; Рейнхардт, Иоахим (9 марта 2013 г.). Квантовая электродинамика . Springer Science & Business Media. ISBN 978-3-662-05246-4 .

[85] Либофф, Ричард Л. (2003). Вводная квантовая механика (4-е изд.). Сан-Франциско: Pearson Education. ISBN 978-81-317-0441-7 .

[86] Барут, АО (1 августа 1978 г.). «Создание фотона: эвристический расчет постоянной Планка ħ или постоянной тонкой структуры α» . Zeitschrift für Naturforschung A. 33 (8): 993–994. Бибкод : 1978ЗНатА..33..993Б . дои : 10.1515/zna-1978-0819 . S2CID 45829793 .

[87] Косия, Лукас; С любовью, Питер (12 июля 2018 г.). «Контекстуальность измерения и постоянная Планка». Новый журнал физики . 20 (7): 073020. arXiv : 1711.08066 . Бибкод : 2018NJPh...20g3020K . дои : 10.1088/1367-2630/aacef2 . S2CID 73623448 .

[88] Хамферис, Дэвид (28 ноября 2022 г.). «Неявная структура постоянной Планка» . Европейский журнал прикладной физики . 4 (6): 22–25. doi : 10.24018/ejphysical.2022.4.6.227 . S2CID 254359279 .

[89] Байс, Ф. Александр; Фармер, Дж. Дойн (2008). «Физика информации» . В Адриансе, Питер; ван Бентем, Йохан (ред.). Философия информации . Справочник по философии науки. Том. 8. Амстердам: Северная Голландия. arXiv : 0708.2837 . ISBN 978-0-444-51726-5 .

[91] Хирота, Э.; Сакакима, Х.; Иномата, К. (9 марта 2013 г.). Гигантские устройства магнитосопротивления . Springer Science & Business Media. ISBN 978-3-662-04777-4 .

[92] Гарднер, Джон Х. (1988). «Теория инвариантности». Энциклия . 65 : 139.

[93] Левин, Рафаэль Д. (4 июня 2009 г.). Динамика молекулярных реакций . Издательство Кембриджского университета. ISBN 978-1-139-44287-9 .

[bohr1-94] Бор, Н. (июль 1913 г.). «I. О строении атомов и молекул» . Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 26 (151): 1–25. Бибкод : 1913PMag...26....1B . дои : 10.1080/14786441308634955 .

[Mehra_and_Rechenberg_v1p1-96] Перейти обратно: ^а ^б Мехра, Джагдиш ; Рехенберг, Гельмут (3 августа 1982 г.). Историческое развитие квантовой теории . Том. 1. Спрингер Нью-Йорк. ISBN 978-0-387-90642-3 .

[97] Зоммерфельд, А. (1915). «К теории рядов Бальмера» (PDF) . Протоколы заседаний математического и физического класса КБ Академии наук в Мюнхене . 33 (198): 425–458. дои : 10.1140/epjh/e2013-40053-8 .

[98] Шварцшильд, К. (1916). «О квантовой гипотезе». Труды Королевской прусской академии наук в Берлине : 548–568.

[99] Эренфест, П. (июнь 1917 г.). «XLVIII. Адиабатические инварианты и теория квантов». Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 33 (198): 500–513. дои : 10.1080/14786440608635664 .

[100] Ланде, А. (июнь 1919 г.). «Серийный спектр гелия». Физический журнал . 20 :228-234.

[101] Бор, Н. (октябрь 1920 г.). «О рядовом спектре элементов». Журнал физики . 2 (5): 423–469. Бибкод : 1920ZPhy....2..423B . дои : 10.1007/BF01329978 .

[102] Стерн, Отто (декабрь 1921 г.). «Путь к экспериментальной проверке направленного квантования в магнитном поле» . Журнал физики . 7 (1): 249–253. Бибкод : 1921ZPhy....7..249S . дои : 10.1007/BF01332793 .

[103] Гейзенберг, Вернер (декабрь 1922 г.). «К квантовой теории линейной структуры и аномальным зеемановским отражениям». Журнал физики . 8 (1): 273–297. Бибкод : 1922ZPhy....8..273H . дои : 10.1007/BF01329602 .

[104] Крамерс, Х.А. Паули, В. (декабрь 1923 г.). «К теории зонных спектров» . Журнал физики . 13 (1): 351–367. Бибкод : 1923ZPhy...13..351K . дои : 10.1007/BF01328226 .

[105] Борн, М .; Джордан, П. (декабрь 1925 г.). «О квантовой механике». Журнал физики . 34 (1): 858–888. Бибкод : 1925ZPhy...34..858B . дои : 10.1007/BF01328531 .

[106] Дирак, ПАМ (декабрь 1925 г.). «Основные уравнения квантовой механики» . Труды Лондонского королевского общества. Серия А, содержащая статьи математического и физического характера . 109 (752): 642–653. Бибкод : 1925RSPSA.109..642D . дои : 10.1098/rspa.1925.0150 .

[107] Борн, М .; Гейзенберг, В .; Джордан, П. (август 1926 г.). «О квантовой механике. II». Журнал физики . 35 (8–9): 557–615. Бибкод : 1926ZPhy...35..557B . дои : 10.1007/BF01379806 .

[Schrodinger_1926_Erste-109] Шрёдингер, Э. (1926). «Квантование как проблема собственных значений» . Анналы физики . 384 (4): 361–376. Бибкод : 1926АнП...384..361С . дои : 10.1002/andp.19263840404 .

[110] Дирак, ПАМ (октябрь 1926 г.). «К теории квантовой механики» . Труды Лондонского королевского общества. Серия А, содержащая статьи математического и физического характера . 112 (762): 661–677. Бибкод : 1926RSPSA.112..661D . дои : 10.1098/rspa.1926.0133 .

[Mehra_and_Rechenberg_v6-111] Перейти обратно: ^а ^б Мехра, Джагдиш ; Рехенберг, Гельмут (2000). Историческое развитие квантовой теории . Том. 6. Нью-Йорк: Спрингер.

[112] Дирак, ПАМ (1930). Принципы квантовой механики (1-е изд.). Оксфорд, Великобритания: Кларендон.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

336

[39]

[40]

482

[41]

104

[42]

[43]

5

[44]

788

[45]

726

[46]

10

[47]

-

[48]

334

[49]

IX

[50]

112

[51]

275

[52]

хв

[53]

148

[54]

604

[55]

313

[56]

[57]

восемнадцатый

[58]

17

[59]

187

[60]

273

[61]

14

[62]

558

[63]

561

[64]

55

[а]

[90]

43

[91]

151

[92]

21

[93]

15

[б]

[94]

180