Анализ чувствительности

Анализ чувствительности — это исследование того, как неопределенность выходных данных математической модели или системы (числовая или иная) может быть разделена и распределена по различным источникам неопределенности на входных данных. Связанной с этим практикой является анализ неопределенности , в котором большее внимание уделяется количественной оценке неопределенности и распространению неопределенности ; в идеале анализ неопределенности и чувствительности должен проводиться одновременно.

Процесс пересчета результатов при альтернативных предположениях для определения влияния переменной при анализе чувствительности может быть полезен для ряда целей: включая:

• Проверка устойчивости результатов модели или системы в условиях неопределенности.
• Более глубокое понимание взаимосвязей между входными и выходными переменными в системе или модели.
• Снижение неопределенности за счет выявления входных данных модели, которые вызывают значительную неопределенность в выходных данных и поэтому должны быть в центре внимания для повышения надежности (возможно, путем дальнейших исследований).
• Поиск ошибок в модели (путем обнаружения неожиданных связей между входными и выходными данными).
• Упрощение модели — исправление входных данных модели, которые не влияют на выходные данные, или выявление и удаление избыточных частей структуры модели.
• Улучшение взаимодействия между разработчиками моделей и лицами, принимающими решения (например, делая рекомендации более достоверными, понятными, убедительными или убедительными).
• Поиск областей в пространстве входных факторов, для которых выходные данные модели максимальны или минимальны или соответствуют некоторому оптимальному критерию (см. оптимизацию и фильтрацию Монте-Карло).
• В случае калибровки моделей с большим количеством параметров первичный тест на чувствительность может облегчить этап калибровки, сосредоточив внимание на чувствительных параметрах. Незнание чувствительности параметров может привести к бесполезной трате времени на нечувствительные параметры.
• Стремиться выявить важные связи между наблюдениями, входными данными модели и прогнозами или прогнозами, что приведет к разработке более эффективных моделей.

Обзор

( Математическая модель например, в биологии, изменении климата, экономике или технике) может быть очень сложной, и в результате ее взаимосвязь между входными и выходными данными может быть плохо понята. В таких случаях модель можно рассматривать как черный ящик , т.е. выходные данные представляют собой «непрозрачную» функцию входных данных. Довольно часто некоторые или все входные данные модели подвержены источникам неопределенности , включая ошибки измерения , отсутствие информации и плохое или частичное понимание движущих сил и механизмов. Эта неопределенность накладывает ограничения на нашу уверенность в ответе или результатах модели. Кроме того, моделям, возможно, придется учитывать естественную внутреннюю изменчивость системы (алеаторию), например возникновение стохастических событий.

В моделях, включающих множество входных переменных, анализ чувствительности является важным компонентом построения модели и обеспечения качества. Национальные и международные агентства, участвующие в исследованиях по оценке воздействия , включили в свои руководства разделы, посвященные анализу чувствительности. Примерами являются Европейская комиссия (см., например, руководящие принципы оценки воздействия ), Белого дома Административно-бюджетное управление , Межправительственная группа экспертов по изменению климата и руководящие принципы моделирования Агентства по охране окружающей среды США .

Настройки, ограничения и связанные с ними проблемы

Настройки и ограничения

Выбор метода анализа чувствительности обычно диктуется рядом ограничений или настроек задачи. Некоторые из наиболее распространенных:

• Затраты на вычисления: анализ чувствительности почти всегда выполняется путем прогона модели (возможно, большого) количества раз, т.е. подход, основанный на выборке . Это может стать серьезной проблемой, если
  • Один прогон модели занимает значительное количество времени (минуты, часы или больше). Это не является чем-то необычным для очень сложных моделей.
  • Модель имеет большое количество неопределенных входных данных. Анализ чувствительности — это, по сути, исследование многомерного входного пространства , размер которого растет экспоненциально с увеличением количества входных данных. См. проклятие размерности .

Затраты на вычисления являются проблемой во многих практических анализах чувствительности. Некоторые методы снижения вычислительных затрат включают использование эмуляторов (для больших моделей) и методов скрининга (для уменьшения размерности задачи). Другой метод — использовать метод анализа чувствительности на основе событий для выбора переменных для приложений, ограниченных по времени. Это метод выбора входной переменной (IVS), который собирает информацию об изменении входных и выходных данных системы с использованием анализа чувствительности для создания матрицы входных/выходных триггеров/событий, которая предназначена для отображения взаимосвязей между входными данными как причинами. которые запускают события, и выходные данные, описывающие фактические события. Причинно-следственная связь между причинами изменения состояния, т.е. входными переменными, и выходными параметрами системы эффектов определяет, какой набор входных данных оказывает реальное влияние на данный выходной результат. Этот метод имеет явное преимущество перед аналитическим и вычислительным методом IVS, поскольку он пытается понять и интерпретировать изменение состояния системы в кратчайшие сроки с минимальными вычислительными затратами.

• Коррелированные входные данные. Большинство распространенных методов анализа чувствительности предполагают независимость входных данных модели, но иногда входные данные могут быть сильно коррелированы. Это все еще незрелая область исследований, и окончательные методы еще не созданы.
• Нелинейность. Некоторые подходы к анализу чувствительности, например, основанные на линейной регрессии , могут неточно измерить чувствительность, когда реакция модели нелинейна по отношению к ее входным данным. В таких случаях измерения, основанные на дисперсии . более подходящими являются
• Множественные выходные данные. Практически все методы анализа чувствительности рассматривают один одномерный выходной результат модели, однако многие модели выдают большое количество, возможно, пространственных или временных данных. Обратите внимание, что это не исключает возможности проведения различных анализов чувствительности для каждого интересующего результата. Однако для моделей, в которых выходные данные коррелируют, показатели чувствительности может быть сложно интерпретировать.

Предположения против выводов

В анализе неопределенности и чувствительности существует решающий компромисс между тем, насколько скрупулезно аналитик исследует исходные предположения , и насколько широкими могут быть полученные в результате выводы . Эту точку зрения хорошо иллюстрирует эконометрик Эдвард Э. Лимер :

Я предложил форму организованного анализа чувствительности, которую я называю «анализом глобальной чувствительности», в котором выбирается окрестность альтернативных предположений и определяется соответствующий интервал выводов. Выводы считаются надежными только в том случае, если окрестность предположений достаточно широка, чтобы быть достоверными, а соответствующий интервал выводов достаточно узок, чтобы быть полезными.

Обратите внимание, что Лимер подчеркивает необходимость «достоверности» при выборе предположений. Самый простой способ признать модель недействительной — продемонстрировать, что она хрупка по отношению к неопределенности в предположениях, или показать, что ее предположения не были приняты «достаточно широко». Ту же концепцию выражает Джером Р. Равец, для которого плохое моделирование означает, что неопределенности во входных данных необходимо подавлять, чтобы результаты не стали неопределенными.

Подводные камни и трудности

Некоторые распространенные трудности при анализе чувствительности включают:

• Слишком много входных данных модели для анализа. Для уменьшения размерности можно использовать экранирование. Другой способ справиться с проклятием размерности — использовать выборку на основе последовательностей с низким расхождением.
• Модель работает слишком долго. Эмуляторы (включая HDMR ) могут сократить общее время за счет ускорения модели или уменьшения количества необходимых запусков модели.
• Недостаточно информации для построения вероятностных распределений входных данных. Распределения вероятностей можно построить на основе данных экспертов , хотя даже в этом случае построить распределения с большой уверенностью может оказаться затруднительно. Субъективность вероятностных распределений или диапазонов сильно повлияет на анализ чувствительности.
• Непонятна цель анализа. К проблеме применяются различные статистические тесты и меры и получаются различные ранжирования факторов. Вместо этого тест должен быть адаптирован к цели анализа, например, используется фильтрация Монте-Карло, если вас интересует, какие факторы наиболее ответственны за формирование высоких/низких значений выходных данных.
• Учитывается слишком много выходных данных модели. Это может быть приемлемо для обеспечения качества подмоделей, но этого следует избегать при представлении результатов общего анализа.
• Кусочная чувствительность. Это когда анализ чувствительности выполняется по одной подмодели за раз. Этот подход неконсервативен, поскольку он может упускать из виду взаимодействие между факторами в различных подмоделях (ошибка II рода).

Методы анализа чувствительности

Идеальная схема возможного анализа чувствительности на основе выборки. Неопределенность, возникающая из различных источников – ошибок в данных, процедуры оценки параметров, альтернативных структур модели – распространяется через модель для анализа неопределенности, а их относительная важность оценивается количественно с помощью анализа чувствительности.

Анализ чувствительности на основе выборки с помощью диаграмм рассеяния. Y (вертикальная ось) является функцией четырех факторов. Точки на четырех диаграммах рассеяния всегда одни и те же, хотя и отсортированы по-разному, т.е. по Z ₁ , Z ₂ , Z ₃ , Z ₄ по очереди. Обратите внимание, что абсцисса различна для каждого графика: (−5, +5) для Z ₁ , (−8, +8) для Z ₂ , (−10, +10) для Z ₃ и Z ₄ . Z ₄ наиболее важен для влияния на Y, большую «форму» поскольку он придает Y .

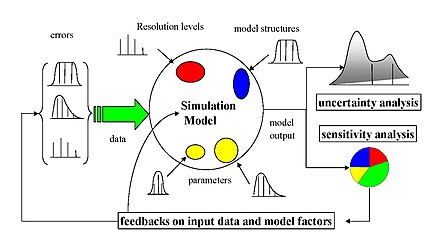
Существует большое количество подходов к проведению анализа чувствительности, многие из которых были разработаны для устранения одного или нескольких ограничений, обсуждавшихся выше. Они также различаются по типу меры чувствительности, будь то на основе (например) дисперсионного разложения , частных производных или элементарных эффектов . Однако в целом большинство процедур придерживаются следующей схемы:

1. Определите количественно неопределенность каждого входного параметра (например, диапазоны, распределения вероятностей). Обратите внимание, что это может быть сложно, и существует множество методов для определения распределения неопределенности на основе субъективных данных.
2. Определите выходные данные модели, подлежащие анализу (цель интереса в идеале должна иметь прямое отношение к проблеме, решаемой моделью).
3. Запустите модель несколько раз, используя определенный план экспериментов . диктуется выбором метода и входной неопределенностью.
4. Используя полученные результаты модели, рассчитайте интересующие показатели чувствительности.

В некоторых случаях эта процедура будет повторяться, например, в задачах большой размерности, когда пользователю приходится отсеивать несущественные переменные перед выполнением полного анализа чувствительности.

Различные типы «основных методов» (обсуждаемые ниже) отличаются различными рассчитываемыми показателями чувствительности. Эти категории могут каким-то образом пересекаться. Могут быть предложены альтернативные способы получения этих показателей с учетом ограничений проблемы.

По одному (ОАТ)

Основная статья: Однофакторный метод

Один из самых простых и распространенных подходов — это изменение по одному фактору за раз (OAT), чтобы увидеть, какое влияние это окажет на результат. ОАТ обычно включает в себя

• перемещение одной входной переменной, сохранение базовых (номинальных) значений других, затем
• возвращая переменной ее номинальное значение, а затем повторяя действия для каждого из остальных входов таким же образом.

Чувствительность затем можно измерить путем мониторинга изменений выходных данных, например, с помощью частных производных или линейной регрессии . Это кажется логичным подходом, поскольку любое изменение, наблюдаемое в выходных данных, будет однозначно связано с изменением одной переменной. Более того, изменяя одну переменную за раз, можно сохранить центральные или базовые значения всех остальных переменных. Это увеличивает сопоставимость результатов (все «эффекты» рассчитываются относительно одной и той же центральной точки пространства) и сводит к минимуму вероятность сбоя компьютерной программы, что более вероятно, когда несколько входных факторов изменяются одновременно.Разработчики моделей часто предпочитают OAT по практическим причинам. В случае сбоя модели при анализе OAT разработчик модели немедленно узнает, какой входной фактор ответственен за сбой.

Однако, несмотря на свою простоту, этот подход не полностью исследует входное пространство, поскольку не учитывает одновременное изменение входных переменных. Это означает, что подход OAT не может обнаружить наличие взаимодействий между входными переменными и непригоден для нелинейных моделей.

Доля входного пространства, которая остается неисследованной при использовании подхода OAT, растет суперэкспоненциально с увеличением количества входных данных. Например, пространство параметров с тремя переменными, которое исследуется по одной, эквивалентно взятию точек вдоль осей x, y и z куба с центром в начале координат. Выпуклая оболочка, ограничивающая все эти точки, представляет собой октаэдр , объем которого составляет лишь 1/6 от общего пространства параметров. В более общем смысле, выпуклая оболочка осей гиперпрямоугольника образует гипероктаэдр , объемная доля которого составляет $1/n!$. При наличии 5 входов исследуемое пространство уже падает до менее 1% от общего пространства параметров. И даже это завышенная оценка, поскольку внеосевой объем фактически вообще не дискретизируется. Сравните это со случайной выборкой пространства, где выпуклая оболочка приближается ко всему объему по мере добавления новых точек. Хотя разреженность OAT теоретически не является проблемой для линейных моделей , истинная линейность в природе встречается редко.

Локальные методы на основе производных

Методы, основанные на локальной производной, включают в себя получение частной производной выходного сигнала Y по входному коэффициенту X _i :

$\left|{\frac {\partial Y}{\partial X_{i}}}\right|_{{\textbf {x}}^{0}},$

где индекс x ⁰ указывает, что производная берется в некоторой фиксированной точке входного пространства (отсюда и слово «локальный» в названии класса). Сопряженное моделирование и автоматическая дифференциация — это методы, которые позволяют вычислять все частные производные затрачивая максимум в 4–6 раз больше, чем затраты на вычисление исходной функции. Подобно OAT, локальные методы не пытаются полностью исследовать входное пространство, поскольку они исследуют небольшие возмущения, обычно по одной переменной за раз. Можно выбрать аналогичные образцы на основе чувствительности на основе производных с помощью нейронных сетей и выполнить количественную оценку неопределенности.

Одним из преимуществ локальных методов является то, что можно составить матрицу для представления всех уязвимостей системы, обеспечивая таким образом обзор, которого невозможно достичь с помощью глобальных методов, если имеется большое количество входных и выходных переменных.

Регрессионный анализ

Регрессионный анализ в контексте анализа чувствительности включает в себя подгонку линейной регрессии к отклику модели и использование стандартизированных коэффициентов регрессии в качестве прямых мер чувствительности. Регрессия должна быть линейной по отношению к данным (т. е. гиперплоскости, следовательно, без квадратичных членов и т. д. в качестве регрессоров), поскольку в противном случае трудно интерпретировать стандартизованные коэффициенты. Поэтому этот метод наиболее подходит, когда реакция модели фактически линейна; линейность может быть подтверждена, например, если коэффициент детерминации велик. Преимущества регрессионного анализа заключаются в его простоте и низких вычислительных затратах.

Методы, основанные на дисперсии

Основная статья: Анализ чувствительности на основе отклонений

Методы, основанные на дисперсии представляют собой класс вероятностных подходов, которые количественно определяют входные и выходные неопределенности как распределения вероятностей и разлагают выходную дисперсию на части, относящиеся к входным переменным и комбинациям переменных. Таким образом, чувствительность выходных данных к входной переменной измеряется величиной отклонений выходных данных, вызванных этими входными данными. Их можно выразить как условные ожидания, т. е., рассматривая модель Y = f ( X ) для X = { X ₁ , X ₂ , ... X _k }, мера чувствительности i -й переменной X _i задается как ,

$\operatorname {Var} \left(E_{{\textbf {X}}_{\sim i}}\left(Y\mid X_{i}\right)\right)$

где «Var» и « E » обозначают операторы дисперсии и ожидаемого значения соответственно, а X _~i обозначает набор всех входных переменных, кроме X _i . Это выражение по существу измеряет вклад только X _i в неопределенность (дисперсию) Y (усредненную по вариациям других переменных) и известно как индекс чувствительности первого порядка или индекс основного эффекта . Важно отметить, что он не измеряет неопределенность, вызванную взаимодействием с другими переменными. Дополнительная мера, известная как индекс общего эффекта , дает общую дисперсию Y , вызванную X _i и его взаимодействием с любой другой входной переменной. Обе величины обычно стандартизируются путем деления на Var( Y ).

Методы, основанные на дисперсии, позволяют полностью исследовать входное пространство, учитывать взаимодействия и нелинейные реакции. По этим причинам они широко используются, когда возможно их вычислить. Обычно этот расчет включает использование методов Монте-Карло , но, поскольку он может включать в себя многие тысячи прогонов модели, при необходимости можно использовать другие методы (например, эмуляторы) для сокращения вычислительных затрат.

Вариограммный анализ поверхностей отклика ( VARS )

Одним из основных недостатков предыдущих методов анализа чувствительности является то, что ни один из них не учитывает пространственно упорядоченную структуру поверхности отклика/выходных данных модели Y = f ( X ) в пространстве параметров. Используя концепции направленных вариограмм и ковариограмм, вариограммный анализ поверхностей отклика (VARS) устраняет этот недостаток путем распознавания пространственно непрерывной структуры корреляции со значениями Y и, следовательно, также со значениями ${\frac {\partial Y}{\partial x_{i}}}$.

По сути, чем выше изменчивость, тем более неоднородной является поверхность отклика в определенном направлении/параметре в определенном масштабе возмущений. Соответственно, в рамках VARS значения направленных вариограмм для данного масштаба возмущений можно рассматривать как комплексную иллюстрацию информации о чувствительности путем увязки анализа вариограмм с концепциями как направления, так и масштаба возмущений. В результате структура VARS учитывает тот факт, что чувствительность является концепцией, зависящей от масштаба, и, таким образом, преодолевает проблему масштаба традиционных методов анализа чувствительности. Что еще более важно, VARS способен обеспечить относительно стабильные и статистически надежные оценки чувствительности параметров при гораздо меньших вычислительных затратах, чем другие стратегии (примерно на два порядка более эффективные). Примечательно, что было показано, что существует теоретическая связь между структурой VARS и подходами, основанными на дисперсии и производной.

Альтернативные методы

Был разработан ряд методов для преодоления некоторых из ограничений, обсуждавшихся выше, которые в противном случае сделали бы оценку показателей чувствительности невозможной (чаще всего из-за вычислительных затрат ). Как правило, эти методы направлены на эффективный расчет показателей чувствительности на основе дисперсии.

Эмуляторы

Эмуляторы (также известные как метамодели, суррогатные модели или поверхности отклика) — это подходы к моделированию данных / машинному обучению , которые включают в себя создание относительно простой математической функции, известной как эмулятор , которая аппроксимирует поведение ввода/вывода самой модели. Другими словами, это понятие «моделирование модели» (отсюда и название «метамодель»). Идея состоит в том, что, хотя компьютерные модели могут представлять собой очень сложную серию уравнений, решение которых может занять много времени, их всегда можно рассматривать как функцию входных данных Y = f ( X ). Запустив модель в нескольких точках входного пространства, можно будет подобрать гораздо более простой эмулятор η ( X ), такой, что η ( X ) ≈ f ( X ) с допустимой погрешностью. Затем меры чувствительности можно рассчитать с помощью эмулятора (либо с помощью Монте-Карло, либо аналитически), что потребует незначительных дополнительных вычислительных затрат. Важно отметить, что количество прогонов модели, необходимых для адаптации к эмулятору, может быть на порядки меньше, чем количество прогонов, необходимых для непосредственной оценки показателей чувствительности модели.

Очевидно, что суть подхода к эмулятору состоит в том, чтобы найти η (эмулятор), который является достаточно близким приближением к модели f . Для этого необходимо выполнить следующие шаги,

1. Выборка (запуск) модели в нескольких точках ее входного пространства. Для этого необходим образец дизайна.
2. Выбор типа эмулятора (математической функции) для использования.
3. «Обучение» эмулятора с использованием образцов данных из модели — обычно это включает в себя настройку параметров эмулятора до тех пор, пока эмулятор не будет максимально имитировать истинную модель.

Выборка модели часто может выполняться с использованием последовательностей с низким расхождением , таких как последовательность Соболя , предложенная математиком Ильей М. Соболем , или выборка латинского гиперкуба , хотя можно также использовать случайные планы, но с потерей некоторой эффективности. Выбор типа эмулятора и обучение неразрывно связаны, поскольку метод обучения будет зависеть от класса эмулятора. Некоторые типы эмуляторов, которые успешно использовались для анализа чувствительности, включают:

• Гауссовские процессы (также известный как кригинг ), где предполагается, что любая комбинация выходных точек распределяется как многомерное распределение Гаусса . Недавно «деревовидные» гауссовские процессы стали использоваться для работы с гетероскедастическими и прерывистыми реакциями.
• Случайные леса , большое количество деревьев решений и усредняется результат. в котором обучается
• Повышение градиента , где последовательность простых регрессий используется для взвешивания точек данных с целью последовательного уменьшения ошибки.
• Полиномиальные разложения хаоса , которые используют ортогональные полиномы для аппроксимации поверхности отклика.
• Сглаживание сплайнов , обычно используется в сочетании с усечениями HDMR (см. ниже).
• Дискретные байесовские сети , в сочетании с каноническими моделями, такими как шумные модели. Шумные модели используют информацию об условной независимости между переменными, чтобы значительно уменьшить размерность.

Использование эмулятора создает проблему машинного обучения , которая может оказаться сложной, если реакция модели сильно нелинейна . Во всех случаях полезно проверить точность работы эмулятора, например, с помощью перекрестной проверки .

Представления многомерных моделей (HDMR)

( Представление многомерной модели HDMR) (термин принадлежит Х. Рабицу ) по сути представляет собой подход эмулятора, который включает в себя разложение вывода функции на линейную комбинацию входных терминов и взаимодействий возрастающей размерности. Подход HDMR использует тот факт, что модель обычно можно хорошо аппроксимировать, пренебрегая взаимодействиями более высокого порядка (второго или третьего порядка и выше). Затем каждый из членов усеченного ряда может быть аппроксимирован, например, полиномами или сплайнами (REFS), а ответ выражен как сумма основных эффектов и взаимодействий до порядка усечения. С этой точки зрения HDMR можно рассматривать как эмуляторы, которые пренебрегают взаимодействиями высокого порядка; Преимущество состоит в том, что они способны эмулировать модели более высокой размерности, чем эмуляторы полного порядка.

Тест амплитудной чувствительности Фурье (FAST)

Основная статья: Тестирование амплитудной чувствительности Фурье

Тест амплитудной чувствительности Фурье (FAST) использует ряд Фурье для представления многомерной функции (модели) в частотной области с использованием одной частотной переменной. Таким образом, интегралы, необходимые для расчета индексов чувствительности, становятся одномерными, что приводит к экономии вычислительных ресурсов.

Фильтрация Монте-Карло

Анализ чувствительности с помощью фильтрации Монте-Карло также является подходом, основанным на выборке, целью которого является выявление областей в пространстве входных факторов, соответствующих конкретным значениям (например, высоким или низким) выходных данных.

Эффекты Шепли

Эффекты Шепли основаны на значениях Шепли и представляют собой средний предельный вклад данного фактора во все возможные комбинации факторов. Эти значения связаны с индексами Соболя, поскольку их значение находится между эффектом Соболя первого порядка и эффектом общего порядка.

Приложения

Примеры анализа чувствительности можно найти в различных областях применения, таких как:

• Науки об окружающей среде
• Бизнес
• Социальные науки
• Химия
• Инженерное дело
• Эпидемиология
• Мета-анализ
• Многокритериальное принятие решений
• Принятие срочных решений
• Калибровка модели
• Количественная оценка неопределенности
• Теория хаоса
  • В популяционной генетике . Станет ли популяция хаотичной, когда наступит период стохастичности.

Аудит чувствительности

Основная статья: Аудит чувствительности

Может случиться так, что анализ чувствительности исследования, основанного на модели, предназначен для обоснования вывода и подтверждения его надежности в контексте, когда вывод влияет на политику или процесс принятия решений. В этих случаях структура самого анализа, его институциональный контекст и мотивы его автора могут стать вопросом огромной важности, а чистый анализ чувствительности – с его акцентом на параметрической неопределенности – может рассматриваться как недостаточный. Акцент на формулировке может быть обусловлен, среди прочего, актуальностью политического исследования для различных групп населения, которые характеризуются разными нормами и ценностями, и, следовательно, из-за разной истории о том, «в чем проблема» и, прежде всего, о том, «кто говорит история». Чаще всего формулировка включает в себя более или менее неявные предположения, которые могут быть как политическими (например, какая группа нуждается в защите), так и техническими (например, какую переменную можно рассматривать как константу).

Чтобы принять во внимание эти опасения, инструменты SA были расширены, чтобы обеспечить оценку всего процесса создания знаний и моделей. Этот подход получил название «аудит чувствительности». Он черпает вдохновение из NUSAP, метод, используемый для определения ценности количественной информации с помощью создания «родословных» чисел. Аудит чувствительности был специально разработан для состязательного контекста, когда не только характер доказательств, но также степень определенности и неопределенности, связанных с доказательствами, будут предметом партийных интересов. Аудит чувствительности рекомендуется в руководящих принципах Европейской комиссии по оценке воздействия. а также в отчете «Научные рекомендации для политики европейских академий».

Связанные понятия

Анализ чувствительности тесно связан с анализом неопределенности; в то время как последний изучает общую неопределенность в выводах исследования, анализ чувствительности пытается определить, какой источник неопределенности больше влияет на выводы исследования.

Постановка задачи анализа чувствительности также имеет большое сходство с областью планирования экспериментов . При планировании экспериментов изучается влияние некоторого процесса или вмешательства («лечение») на некоторые объекты («экспериментальные единицы»). При анализе чувствительности рассматривается влияние изменения входных данных математической модели на выходные данные самой модели. В обеих дисциплинах стремятся получить информацию от системы с минимумом физических или численных экспериментов.

См. также

• Причинность
• Метод элементарных эффектов
• Экспериментальный анализ неопределенности
• Тестирование амплитудной чувствительности Фурье
• Теория принятия решений при информационном дефиците
• Интервал ПЯТЬ
• Анализ возмущений
• Вероятностный дизайн
• Анализ границ вероятности
• Робастификация
• ROC-кривая
• Количественная оценка неопределенности
• Анализ чувствительности на основе отклонений
• Анализ мультивселенной
• Выбор функции

Дальнейшее чтение

• Каннаво, Ф. (2012). «Анализ чувствительности для оценки качества моделирования вулканических источников и выбора модели». Компьютеры и геонауки . 44 : 52–59. Бибкод : 2012CG.....44...52C . дои : 10.1016/j.cageo.2012.03.008 .
• Фассо А. (2007) «Статистический анализ чувствительности и качество воды». В книге Уаймер Л. Эд, Статистическая основа критериев и мониторинга качества воды . Уайли, Нью-Йорк.
• Фассо А., Перри П.Ф. (2002) «Анализ чувствительности». Абделя Х. Эль-Шарави и Уолтера В. Пигорша (редакторы) В Энциклопедии экологической метрики , том 4, стр. 1968–1982, Wiley.
• Фассо А., Эспозито Э., Порку Э., Ревербери А.П., Вельо Ф. (2003) «Статистический анализ чувствительности насадочных колонных реакторов к загрязненным сточным водам». Экологометрия . Том. 14, № 8, 743–759.
• Хауг, Эдвард Дж.; Чой, Кён К.; Комков, Вадим (1986) Анализ чувствительности конструктивных систем . Математика в науке и технике, 177. Academic Press, Inc., Орландо, Флорида.
• Пианози, Ф.; Бевен, К.; Фрир, Дж.; Холл, JW; Ружье, Дж.; Стивенсон, Д.Б.; Вагенер, Т. (2016). «Анализ чувствительности моделей окружающей среды: систематический обзор с практическим рабочим процессом» . Экологическое моделирование и программное обеспечение . 79 : 214–232. Бибкод : 2016EnvMS..79..214P . дои : 10.1016/j.envsoft.2016.02.008 . hdl : 10871/21086 .
• Пилки, Огайо и Л. Пилки-Джарвис (2007), Бесполезная арифметика. Почему ученые-экологи не могут предсказать будущее. Нью-Йорк: Издательство Колумбийского университета.
• Сантнер, Ти Джей; Уильямс, Би Джей; Нотц, Висконсин (2003) Планирование и анализ компьютерных экспериментов ; Спрингер-Верлаг.
• Талеб, Н.Н., (2007) Черный лебедь: влияние крайне невероятного, Random House.

Внешние ссылки

• Веб-сайт с материалами серии конференций САМО (1995-2025 гг.)
• веб-страница по анализу чувствительности – (Объединенный исследовательский центр Европейской комиссии)
• Проект MUCM. Архивировано 24 апреля 2013 г. в Wayback Machine . Обширные ресурсы для анализа неопределенности и чувствительности моделей, требующих вычислительных затрат.