Правильный косой апейроэдр

Мукуб представляет собой правильный косой апейроэдр.

В геометрии правильный косой апейроэдр — это бесконечный правильный косой многогранник . Они имеют либо перекошенные правильные грани , либо перекошенные правильные фигуры вершин .

История

В 1926 году Джон Флиндерс Петри взял концепцию правильных косых многоугольников , многоугольников, вершины которых не находятся в одной плоскости, и распространил ее на многогранники. Хотя апейроэдры обычно требуются для мозаики двумерной плоскости, Петри рассматривал случаи, когда грани все еще были выпуклыми, но не требовали, чтобы они лежали ровно в плоскости, они могли иметь фигуру вершины перекошенного многоугольника .

Петри открыл два правильных косых апейроэдра: мукуб и мюоктаэдр. Гарольд Скотт Макдональд Коксетер вывел третий, мутетраэдр, и доказал, что эти три элемента являются полными. Согласно определению Коксетера и Петри, требующему выпуклых граней и допускающему перекос фигуры вершины, эти три были не только единственными косыми апейроэдрами в трехмерном евклидовом пространстве, но и единственными косыми многогранниками в трехмерном пространстве, поскольку там Коксетер показал, что не существует конечные случаи.

В 1967 году Гарнер исследовал правильные косые апейроэдры в гиперболическом трехмерном пространстве по определению Петри и Коксетерса, обнаружив 31 правильные косые апейроэдры с компактной или паракомпактной симметрией.

В 1977 году Грюнбаум обобщил косые многогранники, чтобы учесть косые грани. Грюнбаум обнаружил еще 23 косые апейроэдры в трехмерном евклидовом пространстве и 3 в двумерном пространстве, которые перекошены в силу своих граней. 12 многогранников Грюнбаума были сформированы с помощью операции смешения двумерных апейроэдров, а остальные 11 были чистыми, т.е. не могли быть образованы нетривиальным смешиванием. Грюнбаум предположил, что этот новый список является полным для рассматриваемых параметров.

В 1985 году Дресс нашел дополнительный чистый правильный косой апейроэдр в трехмерном пространстве и доказал, что с этим дополнительным косым апейроэдром список был полным.

Правильные косые апейроэдры в евклидовом трехмерном пространстве

Многогранники Петри-Коксетера

Три евклидовых решения в трехмерном пространстве — это {4,6|4}, {6,4|4} и {6,6|3}. Джон Конвей назвал их мукубом, мюоктаэдром и мутетраэдром соответственно, обозначая кратный куб, октаэдр и тетраэдр.

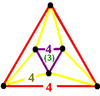
1. Mucube : {4,6|4}: 6 квадратов вокруг каждой вершины (относится к кубическим сотам , построенным из кубических ячеек, удаляющим две противоположные грани из каждой и соединяющим наборы из шести вместе вокруг безликого куба ).
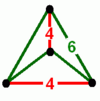
2. Муоктаэдр : {6,4|4}: 4 шестиугольника вокруг каждой вершины (относится к усеченным кубическим сотам , построенным из усеченного октаэдра с удаленными квадратными гранями и соединяющими пары отверстий вместе).
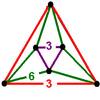
3. Мутетраэдр : {6,6|3}: 6 шестиугольников вокруг каждой вершины (относится к четвертькубическим сотам , построенным из усеченных ячеек тетраэдра, удалению треугольных граней и соединению наборов из четырех вокруг безликого тетраэдра .)

Коксетер дает эти правильные косые апейроэдры {2q,2r|p} с расширенной киральной симметрией [[( p , q , p , r )] ⁺ ] которая, по его словам, изоморфна его абстрактной группе (2 q ,2 r |2, p ). Соответствующие соты имеют расширенную симметрию [[( p , q , p , r )]].

Компактные правильные косые апейроэдры

Группа Коксетера симметрия	Апейроэдр {p,q|l}	Изображение	Лицо {р}	Дыра { л }	Вертекс фигура	Связанный соты
[[4,3,4]] [[4,3,4] + ]	{4,6|4} Раздавить его	анимация				т 0,3 {4,3,4}
	{6,4|4} Муоктаэдр	анимация				2т{4,3,4}
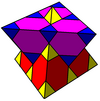
[[3 [4] ]] [[3 [4] ] + ]	{6,6|3} Мутетраэдр	анимация				д{4,3,4}

Многогранники Грюнбаума-Платья

Косые соты

Существует 3 правильных косых апейроэдра полного ранга, также называемых правильными косыми сотами , то есть косыми апейроэдрами в двух измерениях. Как и в случае с конечными косыми многогранниками полного ранга, все три из них могут быть получены путем применения двойственного Петри к плоским многогранникам, в данном случае к трем правильным мозаикам.

В качестве альтернативы их можно построить с помощью операции apeir над правильными многоугольниками. Хотя в Петриале используется классическая конструкция, она плохо распространяется на более высокие ранги. Напротив, операция apeir используется для построения косых сот более высокого ранга.

Операция apeir берет порождающие зеркала многоугольника, ρ ₀ и ρ ₁ , и использует их в качестве зеркал для вершинной фигуры многогранника, новое вершинное зеркало w тогда является точкой, расположенной там, где находится начальная вершина многоугольника (или любом месте зеркала ρ1 _, кроме его пересечения с ρ0 _в ). Новая начальная вершина размещается на пересечении зеркал ρ ₀ и ρ ₁ . Таким образом, апейрный многогранник порождается ⟨w, ρ ₀ , ρ ₀ ⟩ .

Косые соты	Символ Шлефли		Лица	Изображение	Петри двойной	Апир
Петриальная квадратная плитка	{4,4} п	{∞,4} 4	∞ зигзаги		Квадратная плитка	Квадрат
Треугольная мозаика Петриала	{3,6} п	{∞,6} 3	∞ зигзаги		Треугольная плитка	Шестиугольник
Шестиугольная мозаика Петриала	{6,3} п	{∞,3} 6	∞ зигзаги		Шестиугольная плитка	Треугольник

Смешанные апейроэдры

{3,6}#{} с краями одной грани, выделенными красным

Для любых двух правильных многогранников P и Q новый многогранник можно создать с помощью следующего процесса:

• Начните с декартова произведения вершин P на вершины Q .
• Добавьте ребра между любыми двумя вершинами p ₀ × q ₀ и p ₁ × q ₁ тогда и только тогда, когда существует ребро между p ₀ и p ₁ в P и ребро между q ₀ и q ₁ в Q . (Если Q не имеет ребер, добавьте виртуальное ребро, соединяющее его вершину с самим собой.)
• Аналогичным образом добавьте грани в каждый набор вершин, инцидентных одной и той же грани как в P, так и в Q . (Если Q не имеет граней, добавьте виртуальную грань, соединяющую его ребро с самим собой.)
• Повторите то же самое для всех рангов собственных элементов.
• Из полученного многогранника выберите одну компоненту связности.

Для правильных многогранников последний шаг гарантированно даст уникальный результат. новый многогранник называется смесью P # и Q и обозначается P Этот Q .

Эквивалентно смесь можно получить, расположив P и Q в ортогональных пространствах и попарно составив их образующие зеркала.

Смешанные многогранники в трехмерном пространстве можно получить путем объединения двухмерных многогранников с одномерными многогранниками. Единственными двумерными многогранниками являются 6 сот (3 евклидовых мозаики и 3 косых сот ):

• Треугольная мозаика : {3, 6}
• Квадратная мозаика : {4, 4}
• Шестиугольная мозаика : {6, 3}
• Треугольная мозаика Петриала: {3, 6} ^п
• Замощение квадрата Петриала: {4, 4} ^п
• Шестиугольная мозаика Петриала: {6, 3} ^п

Единственными одномерными многогранниками являются:

• : Отрезок линии { }
• Апейрогон } : {∞

Каждая пара между ними создает действительный отдельный правильный косой апейроэдр в трехмерном евклидовом пространстве, всего 12 смешанные косые апейроэдры.

Поскольку скелет квадратной мозаики двудольный , две из этих смесей: {4, 4}#{} и {4, 4} ^п #{} , комбинатриально эквивалентны своим несмешанным аналогам.

Чистые апейроэдры

Некоторые взаимоотношения между 12 чистыми апейроэдрами в трехмерном евклидовом пространстве

• π представляет Петриал
• δ представляет собой двойственный
• η представляет собой разделение пополам
• φ представляет огранку
• σ представляет собой перекос
• r представляет собой исправление

Многогранник считается чистым, если его нельзя выразить как нетривиальную смесь двух многогранников. Смесь считается тривиальной, если она содержит результат в качестве одного из компонентов. Альтернативно, чистый многогранник — это тот, группа симметрии которого не содержит нетривиальных подпредставлений .

Существует 12 правильных чистых апейроэдров в трёх измерениях. Три из них — многогранники Петри-Коксетера :

• {4,6 | 4}
• {6,4 | 4}
• {6,6 | 3}

Еще три получены как Петриалы многогранников Петри-Коксетера:

• {4,6 | 4} ^п = {∞, 4} _6,4
• {6,4 | 4} ^п = {∞, 6} _4,4
• {6,6 | 3} ^п = {∞, 6} _6,3

Три дополнительных чистых апейроэдра могут быть образованы с помощью конечных косых многоугольников в качестве граней:

• 
  6 косых шестиугольников в шестиугольном расположении образуют вершину {6,6} ₄ .
• 
  6 косых квадратов в шестиугольном расположении образуют вершину {4,6} ₆ .
• 
  4 косых шестиугольника , расположенных в квадрате , образуют вершину {6,4} ₆ .

Эти 3 закрыты по операциям Вильсона . Это означает, что каждый может быть построен из любого другого с помощью некоторой комбинации операций Петриала и двойственных операций. {6,6} ₄ самодуален , а {6,4} ₆ само-Петриал.

Правильные косые апейроэдры в гиперболическом трехмерном пространстве

Компактный косой апейроэдр {4,6 | 5}

В 1967 году К.У.Л. Гарнер идентифицировал 31 гиперболический косой апейроэдр с правильных косых многоугольников фигурами вершин , найденных путем расширения многогранников Петри-Коксетера до гиперболического пространства.

Это 14 компактных и 17 паракомпактные правильные косые многогранники в гиперболическом пространстве, построенные на основе симметрии подмножества линейных и циклических графов групп Кокстера вида [[( p , q , p , r )]]. Они определяют правильные косые многогранники {2 q ,2 r | p } и двойственный {2 r ,2 q | п }. Для частного случая групп линейных графов r = 2 это представляет группу Кокстера [ p , q , p ]. Он генерирует регулярные перекосы {2 q , 4 | p } и {4,2 q | п }. Все они существуют как подмножество граней выпуклых однородных сот в гиперболическом пространстве .

Косой апейроэдр имеет ту же самую фигуру вершины антипризмы , что и соты, но реализуются только зигзагообразные грани вершинной фигуры, в то время как другие грани образуют отверстия.

14 Компактные правильные косые апейроэдры

Коксетер группа	Апейроэдр {p,q|l}	Лицо {р}	Дыра {л}	Соты	Вертекс фигура		Апейроэдр {p,q|l}	Лицо {р}	Дыра {л}	Соты	Вертекс фигура
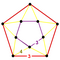
[3,5,3]	{10,4|3}			2т{3,5,3}			{4,10|3}			т 0,3 {3,5,3}
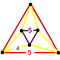
[5,3,5]	{6,4|5}			2т{5,3,5}			{4,6|5}			т 0,3 {5,3,5}
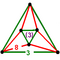
[(4,3,3,3)]	{8,6|3}			ct{(4,3,3,3)}			{6,8|3}			ct{(3,3,4,3)}
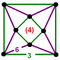
[(5,3,3,3)]	{10,6|3}			ct{(5,3,3,3)}		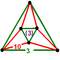	{6,10|3}			ct{(3,3,5,3)}
[(4,3,4,3)]	{8,8|3}			ct{(4,3,4,3)}		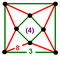	{6,6|4}			ct{(3,4,3,4)}
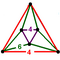
[(5,3,4,3)]	{8,10|3}			ct{(4,3,5,3)}			{10,8|3}			ct{(5,3,4,3)}
[(5,3,5,3)]	{10,10|3}			ct{(5,3,5,3)}			{6,6|5}			ct{(3,5,3,5)}

17 Паракомпактные правильные косые апейроэдры

Коксетер группа	Апейроэдр {p,q|l}	Лицо {р}	Дыра {л}	Соты	Вертекс фигура		Апейроэдр {p,q|l}	Лицо {р}	Дыра {л}	Соты	Вертекс фигура
[4,4,4]	{8,4|4}			2т{4,4,4}			{4,8|4}			т 0,3 {4,4,4}
[3,6,3]	{12,4|3}			2т{3,6,3}		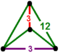	{4,12|3}			т 0,3 {3,6,3}
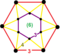
[6,3,6]	{6,4|6}			2т{6,3,6}			{4,6|6}			т 0,3 {6,3,6}
[(4,4,4,3)]	{8,6|4}			ct{(4,4,3,4)}			{6,8|4}			ct{(3,4,4,4)}
[(4,4,4,4)]	{8,8|4}			д{4,4,4}
[(6,3,3,3)]	{12,6|3}			ct{(6,3,3,3)}		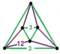	{6,12|3}			ct{(3,3,6,3)}
[(6,3,4,3)]	{12,8|3}			ct{(6,3,4,3)}		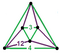	{8,12|3}			ct{(4,3,6,3)}
[(6,3,5,3)]	{12,10|3}			ct{(6,3,5,3)}			{10,12|3}			ct{(5,3,6,3)}
[(6,3,6,3)]	{12,12|3}			ct{(6,3,6,3)}			{6,6|6}			ct{(3,6,3,6)}

См. также

• Косой апейроэдр
• Правильный косой многогранник
• Тетрастикс

Библиография

• Гарнер (1967), «Правильные косые многогранники в гиперболическом трехмерном пространстве», Canadian Journal of Mathematics , 19 : 1179–1186, doi : 10.4153/CJM-1967-106-9
• Грюнбаум, Бранко (1977), «Правильные многогранники - старые и новые» (PDF) , Mathematical Equations , 16 (1–2): 1–20, doi : 10.1007/BF01836414 , S2CID   125049930
• Макмаллен, Питер; Шульте, Эгон (1997). «Правильные многогранники в обычном пространстве» (PDF) . Дискретная и вычислительная геометрия . 17 (47): 449–478. дои : 10.1007/PL00009304 .
• МакМаллен, Питер ; Шульте, Эгон (2002), Абстрактные правильные многогранники , Энциклопедия математики и ее приложений, том. 92, Кембридж: Издательство Кембриджского университета, номер номера : 10.1017/CBO9780511546686 , ISBN.  0-521-81496-0 , г-н   : 1965665
• Макмаллен, Питер (2004). «Правильные многогранники полного ранга» (PDF) . Дискретная вычислительная геометрия . 32 : 1–35. дои : 10.1007/s00454-004-0848-5 .
• Платье, Андреас (1985). «Комбинаторная теория новых правильных многогранников Грюнбаума, Часть II: Полное перечисление». Математические уравнения . 29 : 222–243. дои : 10.1007/BF02189831 . S2CID   121260389 .
• Пересмотр карт Петри-Коксетера PDF , Изабель Хабард, Эгон Шульте, Азия Ивик Вайс, 2005 г.
• Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN   978-1-56881-220-5 ,
• Питер МакМаллен , Четырехмерные правильные многогранники , Дискретная и вычислительная геометрия, сентябрь 2007 г., том 38, выпуск 2, стр. 355–387.
• Коксетер , Правильные многогранники , Третье издание, (1973), Дуврское издание, ISBN   0-486-61480-8
• Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN   978-0-471-01003-6 [1]
  • (Документ 2) HSM Coxeter, «Правильные губки, или косые многогранники», Scripta Mathematica 6 (1939) 240–244.
  • (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380–407, МР 2,10]
  • (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559–591]
• Коксетер , Красота геометрии: двенадцать эссе , Dover Publications, 1999, ISBN   0-486-40919-8 (Глава 5: Правильные косые многогранники в трех и четырех измерениях и их топологические аналоги, Труды Лондонского математического общества, Сер. 2, Том 43, 1937.)
  • Коксетер, HSM Правильные косые многогранники в трех и четырех измерениях. Учеб. Лондонская математика. Соц. 43, 33–62, 1937.