Итерированная функция

Итерационные преобразования объекта слева
Сверху — поворот по часовой стрелке на 90°. Он имеет порядок 4, потому что это наименьший положительный показатель степени, который дает тождество. Ниже показано отображение сдвига с бесконечным порядком.
Ниже приведены их композиции , обе имеют порядок 3.

В математике итерированная функция — это функция, которая получается путем составления другой функции сама с собой два или несколько раз. Процесс многократного применения одной и той же функции называется итерацией . В этом процессе, начиная с некоторого исходного объекта, результат применения данной функции снова подается в функцию в качестве входных данных, и этот процесс повторяется.

Например, на изображении справа:

$L=F(K),\ M=F\circ F(K)=F^{2}(K).$

Итерированные функции изучаются в информатике , фракталах , динамических системах , математике и физике ренормгрупп .

Определение

формальное определение итерированной функции на множестве X. Далее следует

Пусть X — множество, а f : X → X — функция .

Определение f ^н как n -я итерация f , где n — неотрицательное целое число, следующим образом: $$f^{0}~{\stackrel {\mathrm {def} }{=}}~\operatorname {id} _{X}$$и $$f^{n+1}~{\stackrel {\mathrm {def} }{=}}~f\circ f^{n},$$

где id _X — тождественная функция на X и ( f $\circ$ g )( x ) = f ( g ( x )) обозначает композицию функций . Это обозначение было обнаружено Джоном Фредериком Уильямом Гершелем в 1813 году. Гершель выразил благодарность за это Гансу Генриху Бюрману , но не упомянув конкретную ссылку на работу Бюрмана, которая остается неоткрытой.

Поскольку обозначение f ^н может относиться как к итерации (композиции) функции f , так и к возведению в степень функции f (последнее обычно используется в тригонометрии ), некоторые математики решите использовать ∘ для обозначения композиционного значения, написав f ^{∘ n} ( x ) для n -й итерации функции f ( x ) , как, например, f ^∘3 ( x ) значение ж ( ж ( ж ( x ))) . С этой же целью f ^{[ н ]} ( x ) использовал Бенджамин Пирс тогда как Альфред Прингшейм и Жюль Молк предложили ^н вместо этого f ( x ) .

Абелевое свойство и итерационные последовательности

В общем, для всех неотрицательных целых чисел m и n справедливо следующее тождество :

$f^{m}\circ f^{n}=f^{n}\circ f^{m}=f^{m+n}~.$

Это структурно идентично свойству в степень , которое возведения ^м а ^н = а ^{м + н} .

Вообще, для произвольных общих (отрицательных, нецелых и т. д.) индексов m и n это соотношение называется функциональным уравнением сдвига , ср. Уравнение Шредера и уравнение Абеля . В логарифмическом масштабе это сводится к вложенности полиномов Чебышева свойству T _m ( T _n ( x )) = T _{m n} ( x ) , поскольку T _n ( x ) = cos ( n arccos ( x )) .

Отношение ( f ^м ) ^н ( Икс ) знак равно ( ж ^н ) ^м ( Икс ) знак равно ж ^минута ( x ) также имеет место, аналогично свойству возведения в степень, что ( a ^м ) ^н = ( а ^н ) ^м = а ^минута .

Последовательность функций f ^н называется последовательностью Пикара , назван в честь Шарля Эмиля Пикара .

данного x в X последовательность значений f Для ^н ( x ) называется орбитой x ​ .

Если ж ^н ( Икс ) знак равно ж ^{п + м} ( x ) для некоторого целого числа m > 0 орбита называется периодической орбитой . Наименьшее такое значение m для данного x называется периодом орбиты . Сама точка x называется периодической точкой . в Проблема обнаружения цикла информатике — это алгоритмическая проблема поиска первой периодической точки на орбите и периода орбиты.

Фиксированные точки

Если x = f ( x ) для некоторого x из X (то есть период орбиты x равен 1 ), то x называется фиксированной точкой итерированной последовательности. Набор фиксированных точек часто обозначается как Fix ( f ) . Существует ряд теорем о неподвижной точке , которые гарантируют существование неподвижных точек в различных ситуациях, включая теорему Банаха о неподвижной точке и теорему Брауэра о неподвижной точке .

Существует несколько методов ускорения сходимости последовательностей, создаваемых итерациями с фиксированной точкой . Например, метод Эйткена, примененный к повторяющейся фиксированной точке, известен как метод Стеффенсена и обеспечивает квадратичную сходимость.

Ограничивающее поведение

После итерации можно обнаружить, что существуют множества, которые сжимаются и сходятся к одной точке. В таком случае точка, к которой сходится, называется притягивающей фиксированной точкой . И наоборот, итерация может создать впечатление, что точки расходятся от одной точки; это было бы в случае нестабильной фиксированной точки .

Когда точки орбиты сходятся к одному или нескольким пределам, набор точек накопления орбиты известен как предельный набор или ω-предельный набор .

Идеи притяжения и отталкивания обобщаются аналогичным образом; можно разделить итерации на стабильные множества и нестабильные множества в соответствии с поведением небольших окрестностей при итерации. Также см. бесконечные композиции аналитических функций .

Возможны и другие ограничивающие модели поведения; например, блуждающие точки — это точки, которые удаляются и никогда не возвращаются даже близко к тому месту, где они начали.

Инвариантная мера

Если рассматривать эволюцию распределения плотности, а не динамику отдельных точек, то предельное поведение задается инвариантной мерой . Его можно представить как поведение облака точек или облака пыли при повторяющихся итерациях. Инвариантная мера является собственным состоянием оператора Рюэля-Фробениуса-Перрона или оператора переноса , соответствующего собственному значению, равному 1. Меньшие собственные значения соответствуют нестабильным, распадающимся состояниям.

В общем, поскольку повторная итерация соответствует сдвигу, оператору переноса и сопряженному с ним оператору Купмана можно интерпретировать как операторов сдвига действие на пространстве сдвига . Теория подсдвигов конечного типа дает общее представление о многих итерированных функциях, особенно о тех, которые приводят к хаосу.

Дробные итерации и потоки, а также отрицательные итерации

g : R → R — тривиальный функциональный корень пятой степени ж : Р ⁺ → R ⁺ , ж ( Икс ) знак равно грех( Икс ) . Вычисление f ( π ⁄ 6 ) = 1 ⁄ 2 = г ⁵ ( π ⁄ 6 ) показано.

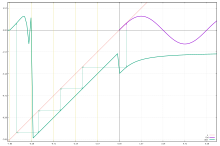
Понятие ф ^{1/ н} следует использовать с осторожностью, когда уравнение g ^н ( x ) = f ( x ) имеет несколько решений, что обычно имеет место, как в уравнении Бэббиджа функциональных корней тождественного отображения. Например, для n = 2 и f ( x ) = 4 x − 6 , g ( x ) = 6 − 2 x и g ( x ) = 2 x − 2 являются решениями; поэтому выражение f ^1/2 ( x ) не обозначает уникальную функцию, так же как числа имеют несколько алгебраических корней. Тривиальный корень f всегда можно получить, если f область определения можно достаточно расширить, ср. картина. Обычно выбираются корни, принадлежащие изучаемой орбите.

Можно определить дробную итерацию функции: например, полуитерация функции f — это функция g такая, что g ( g ( x )) = f ( x ) . Эту функцию g ( x ) можно записать, используя индексное обозначение как f ^1/2 ( х ) . Аналогично, f ^1/3 ( x ) — функция, определенная так, что f ^1/3 ( ж ^1/3 ( ж ^1/3 ( Икс ))) знак равно ж ( Икс ) , а ж ^2/3 ( x ) может быть определен как равный f ^1/3 ( ж ^1/3 ( x )) и т. д., и все это основано на упомянутом ранее принципе, что f ^м ○ ж ^н = е ^{м + н} . Эту идею можно обобщить так, что количество итераций n становится непрерывным параметром , своего рода непрерывным «временем» непрерывной орбиты .

В таких случаях систему называют потоком ( см. раздел о сопряжении ниже).

Если функция является биективной (и, следовательно, обладает обратной функцией), то отрицательные итерации соответствуют обратным функциям и их композициям. Например, ф ⁻¹ ( x ) является нормальной инверсией f , а f ⁻² ( x ) является обратным, составленным из самого себя, т.е. f ⁻² ( Икс ) знак равно ж ⁻¹ ( ж ⁻¹ ( х )) . Дробно-отрицательные итерации определяются аналогично дробно-положительным; например, ф ^−1/2 ( x ) определяется так, что f ^−1/2 ( ж ^−1/2 ( Икс )) = ж ⁻¹ ( x ) или, что то же самое, такой, что f ^−1/2 ( ж ^1/2 ( Икс )) = ж ⁰ ( Икс ) знак равно Икс .

Некоторые формулы для дробной итерации

Один из нескольких методов нахождения формулы ряда для дробной итерации с использованием фиксированной точки заключается в следующем.

1. Сначала определите фиксированную точку для функции такой, что f ( a ) = a .
2. Определить f ^н ( a ) = a для всех n, принадлежащих действительным числам. В каком-то смысле это наиболее естественное дополнительное условие, которое можно наложить на дробные итерации.
3. Развернуть f ^н ( x ) вокруг фиксированной точки a как ряд Тейлора , $$f^{n}(x)=f^{n}(a)+(x-a)\left.{\frac {d}{dx}}f^{n}(x)\right|_{x=a}+{\frac {(x-a)^{2}}{2}}\left.{\frac {d^{2}}{dx^{2}}}f^{n}(x)\right|_{x=a}+\cdots$$
4. Расширить $$f^{n}(x)=f^{n}(a)+(x-a)f'(a)f'(f(a))f'(f^{2}(a))\cdots f'(f^{n-1}(a))+\cdots$$
5. на Замените f ^к ( a ) = a , для любого k , $$f^{n}(x)=a+(x-a)f'(a)^{n}+{\frac {(x-a)^{2}}{2}}(f''(a)f'(a)^{n-1})\left(1+f'(a)+\cdots +f'(a)^{n-1}\right)+\cdots$$
6. Используйте геометрическую прогрессию для упрощения терминов. $$f^{n}(x)=a+(x-a)f'(a)^{n}+{\frac {(x-a)^{2}}{2}}(f''(a)f'(a)^{n-1}){\frac {f'(a)^{n}-1}{f'(a)-1}}+\cdots$$ Существует особый случай, когда f '(a) = 1 , $$f^{n}(x)=x+{\frac {(x-a)^{2}}{2}}(nf''(a))+{\frac {(x-a)^{3}}{6}}\left({\frac {3}{2}}n(n-1)f''(a)^{2}+nf'''(a)\right)+\cdots$$

Это можно продолжать бесконечно, хотя и неэффективно, поскольку последние условия становятся все более сложными. Более систематическая процедура описана в следующем разделе, посвященном сопряжению .

Пример 1

Например, установка f ( x ) = Cx + D дает фиксированную точку a = D /(1 − C ) , поэтому приведенная выше формула завершается просто $$f^{n}(x)={\frac {D}{1-C}}+\left(x-{\frac {D}{1-C}}\right)C^{n}=C^{n}x+{\frac {1-C^{n}}{1-C}}D~,$$что тривиально проверить.

Пример 2

Найдите значение ${\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{\cdots }}}$ где это делается n раз (и, возможно, интерполированные значения, когда n не является целым числом). У нас есть f ( x ) = √ 2 ^х . Неподвижной точкой является a = f (2) = 2 .

Итак, положим x = 1 и f ^н (1) расширенное вокруг значения фиксированной точки 2, тогда представляет собой бесконечную серию, $${\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{\cdots }}}=f^{n}(1)=2-(\ln 2)^{n}+{\frac {(\ln 2)^{n+1}((\ln 2)^{n}-1)}{4(\ln 2-1)}}-\cdots$$что, учитывая только первые три члена, верно до первого десятичного знака, когда n положительно. См. также Тетрация : f. ^н (1) = ^н √ 2 . Использование другой фиксированной точки a = f (4) = 4 приводит к расходимости ряда.

Для n = −1 ряд вычисляет обратную функцию ⁠2 + пер х / пер 2 ⁠ .

Пример 3

С функцией f ( x ) = x ^б , разверните вокруг фиксированной точки 1, чтобы получить ряд $$f^{n}(x)=1+b^{n}(x-1)+{\frac {1}{2}}b^{n}(b^{n}-1)(x-1)^{2}+{\frac {1}{3!}}b^{n}(b^{n}-1)(b^{n}-2)(x-1)^{3}+\cdots ~,$$что представляет собой просто ряд Тейлора для x ^{( б н )} расширился примерно на 1.

Сопряжение

Если f и g — две итерированные функции и существует гомеоморфизм h такой, что g = h ⁻¹ ○ f ○ h , то f и g называются топологически сопряженными .

Очевидно, что топологическая сопряженность сохраняется при итерации, так как g ^н = час ⁻¹ ○ ж ^н ○ час . Таким образом, если можно решить одну итерированную систему функций, у него также есть решения для всех топологически сопряженных систем. Например, карта палаток топологически сопряжена с логистической картой . В частном случае, принимая f ( x ) = x + 1 , имеем итерацию g ( x ) = h ⁻¹ ( час ( x ) + 1) как

г ^н ( Икс ) знак равно час ⁻¹ ( час ( x ) + n ) для любой функции h .

Сделав замену x = h ⁻¹ ( y ) = φ ( y ) дает

g ( φ ( y )) = φ ( y +1) — форма, известная как уравнение Абеля .

Даже в отсутствие строгого гомеоморфизма вблизи неподвижной точки, взятой здесь за точку x = 0, f (0) = 0, часто можно решить Уравнение Шредера для функции Ψ, которое делает f ( x ) локально сопряженным с простой дилатацией, g ( x ) = f '(0) x , то есть

ж ( Икс ) знак равно Ψ ⁻¹ ( ж '(0) Ψ( Икс )) .

Таким образом, его итерационная орбита, или поток, при соответствующих условиях (например, f '(0) ≠ 1 ) представляет собой сопряженную орбиту монома,

P.S. ⁻¹ ( ж '(0) ^н Ψ( x )) ,

где n в этом выражении служит простым показателем степени: функциональная итерация сведена к умножению! Здесь, однако, показатель степени n больше не обязательно должен быть целым или положительным и представляет собой непрерывное «время» эволюции для всей орбиты: моноид ) последовательности Пикара (ср. полугруппа преобразований обобщился до полной непрерывной группы .

Итерирует функцию синуса ( синяя ) в первом полупериоде. Полуитерационный ( оранжевый ), т. е. функциональный квадратный корень синуса; функциональный квадратный корень из этого, четверть итерации (черный) над ним; и дальнейшие дробные итерации до 1/64. Функции под синусоидом ( синий ) представляют собой шесть целочисленных итераций ниже него, начиная со второй итерации ( красный ) и заканчивая 64-й итерацией. Зеленый треугольник конверта представляет собой предельную нулевую итерацию, пилообразная функция служит отправной точкой, ведущей к синусоидальной функции. Пунктирная линия представляет собой отрицательную первую итерацию, т. е. обратную синусоиду (арксину). (С сайта общей педагогики. Обозначения см. в [2] .)

Этот метод (пертурбативное определение главной собственной функции Ψ, ср. матрица Карлемана ) эквивалентен алгоритму предыдущего раздела, хотя на практике является более мощным и систематическим.

Цепи Маркова

Если функция линейна и может быть описана стохастической матрицей , то есть матрицей, сумма строк или столбцов которой равна единице, то итерированная система известна как цепь Маркова .

Примеры

Есть много хаотичных карт . К хорошо известным итеративным функциям относятся множество Мандельброта и системы итерированных функций .

Эрнст Шредер , в 1870 году разработал специальные случаи логистического отображения , такие как хаотический случай f ( x ) = 4 x (1 − x ) , так что Ψ( x ) = arcsin( √ x ) ² , следовательно, f ^н ( х ) = грех (2 ^н дугсин( √ x )) ² .

Нехаотический случай, который Шрёдер также проиллюстрировал своим методом f ( x ) = 2 x (1 − x ) , дал Ψ ( x ) = − ⁠ 1 / 2 ⁠ ln(1 - 2 x ) и, следовательно, f ^н ( Икс ) знак равно - ⁠ 1 / 2 ⁠ ((1 - 2 Икс ) ^{2 н} − 1) .

Если f — действие элемента группы на множество, то итерированная функция соответствует свободной группе .

Большинство функций не имеют явных общих выражений в замкнутой форме для n -й итерации. В таблице ниже перечислены некоторые это делать. Обратите внимание, что все эти выражения действительны даже для нецелых и отрицательных n , а также для неотрицательных целых n .

$f(x)$	$f^{n}(x)$
$x+b$	$x+nb$
$ax+b\ (a\neq 1)$	$a^{n}x+{\frac {a^{n}-1}{a-1}}b$
$ax^{b}\ (b\neq 1)$	$a^{\frac {b^{n}-1}{b-1}}x^{b^{n}}$
$ax^{2}+bx+{\frac {b^{2}-2b}{4a}}$ (см. примечание)	${\frac {2\alpha ^{2^{n}}-b}{2a}}$ где: $\alpha ={\frac {2ax+b}{2}}$
$ax^{2}+bx+{\frac {b^{2}-2b-8}{4a}}$ (см. примечание)	${\frac {2\alpha ^{2^{n}}+2\alpha ^{-2^{n}}-b}{2a}}$ где: $\alpha ={\frac {2ax+b\pm {\sqrt {(2ax+b)^{2}-16}}}{4}}$
${\frac {ax+b}{cx+d}}$ ( дробное линейное преобразование )	${\frac {a}{c}}+{\frac {bc-ad}{c}}\left[{\frac {(cx-a+\alpha )\alpha ^{n-1}-(cx-a+\beta )\beta ^{n-1}}{(cx-a+\alpha )\alpha ^{n}-(cx-a+\beta )\beta ^{n}}}\right]$ где: $\alpha ={\frac {a+d+{\sqrt {(a-d)^{2}+4bc}}}{2}}$ $\beta ={\frac {a+d-{\sqrt {(a-d)^{2}+4bc}}}{2}}$
$g^{-1}{\Big (}h{\bigl (}g(x){\bigr )}{\Big )}$	$g^{-1}{\Bigl (}h^{n}{\bigl (}g(x){\bigr )}{\Bigr )}$
$g^{-1}{\bigl (}g(x)+b{\bigr )}$ (общее уравнение Абеля )	$g^{-1}{\bigl (}g(x)+nb{\bigr )}$
${\sqrt {x^{2}+b}}$	${\sqrt {x^{2}+bn}}$
$g^{-1}{\Bigl (}a\ g(x)+b{\Bigr )}\ (a\neq 1\vee b=0)$	$g^{-1}{\Bigl (}a^{n}g(x)+{\frac {a^{n}-1}{a-1}}b{\Bigr )}$
${\sqrt {ax^{2}+b}}$	${\sqrt {a^{n}x^{2}+{\frac {a^{n}-1}{a-1}}b}}$
$T_{m}(x)=\cos(m\arccos x)$ ( Полином Чебышева для целого числа m )	$T_{mn}=\cos(m^{n}\arccos x)$

Примечание: эти два особых случая топора ² + bx + c — единственные случаи, которые имеют решение в замкнутой форме. Выбор b = 2 = – a и b = 4 = – a соответственно, еще больше сводит их к нехаотичным и хаотичным логистическим случаям, обсуждавшимся перед таблицей.

Некоторые из этих примеров связаны между собой простыми сопряжениями.

Средства обучения

Итерированные функции можно изучать с помощью дзета-функции Артина – Мазура и трансфер-операторов .

В информатике

В информатике итерированные функции встречаются как частный случай рекурсивных функций , которые, в свою очередь, закрепляют изучение таких широких тем, как лямбда-исчисление , или более узких, таких как денотатационная семантика компьютерных программ.

Определения в терминах итерированных функций

Два важных функционала можно определить в терминах итерированных функций. Это суммирование :

$\left\{b+1,\sum _{i=a}^{b}g(i)\right\}\equiv \left(\{i,x\}\rightarrow \{i+1,x+g(i)\}\right)^{b-a+1}\{a,0\}$

и эквивалентный продукт:

$\left\{b+1,\prod _{i=a}^{b}g(i)\right\}\equiv \left(\{i,x\}\rightarrow \{i+1,xg(i)\}\right)^{b-a+1}\{a,1\}$

Функциональная производная

Функциональная производная итерированной функции задается рекурсивной формулой:

${\frac {\delta f^{N}(x)}{\delta f(y)}}=f'(f^{N-1}(x)){\frac {\delta f^{N-1}(x)}{\delta f(y)}}+\delta (f^{N-1}(x)-y)$

Уравнение передачи данных Лия

См. Также: Оператор сдвига § Функции действительной переменной.

Итерированные функции возникают при разложении в ряд комбинированных функций, таких как g ( f ( x )) .

Учитывая скорость итерации или бета-функцию (физика) ,

$v(x)=\left.{\frac {\partial f^{n}(x)}{\partial n}}\right|_{n=0}$

для н ^й итерации функции f , мы имеем

$g(f(x))=\exp \left[v(x){\frac {\partial }{\partial x}}\right]g(x).$

Например, для жесткой адвекции, если f ( x ) = x + t , то v ( x ) = t . Следовательно, g ( x + t ) = exp( t ∂/∂ x ) g ( x ) , действие оператора простого сдвига .

И наоборот, можно указать f ( x ) для произвольного v ( x ) с помощью общего уравнения Абеля , обсуждавшегося выше:

$f(x)=h^{-1}(h(x)+1),$

где

$h(x)=\int {\frac {1}{v(x)}}\,dx.$

Это очевидно, если отметить, что

$f^{n}(x)=h^{-1}(h(x)+n)~.$

Тогда для непрерывного индекса итерации t , теперь записанного в виде нижнего индекса, это равнозначно знаменитой экспоненциальной реализации Ли непрерывной группы:

$e^{t~{\frac {\partial ~~}{\partial h(x)}}}g(x)=g(h^{-1}(h(x)+t))=g(f_{t}(x)).$

Начальной скорости потока v достаточно для определения всего потока, учитывая эту экспоненциальную реализацию, которая автоматически обеспечивает общее решение функционального уравнения перевода ,

$f_{t}(f_{\tau }(x))=f_{t+\tau }(x)~.$

См. также

• Иррациональное вращение
• Итерированная система функций
• Итерационный метод
• Номер вращения
• Теорема Сарковского
• Дробное исчисление
• Рекуррентное отношение
• Уравнение Шредера
• Функциональный квадратный корень
• Функция Абеля
• Уравнение Шредера
• Уравнение Бетчера
• Бесконечные композиции аналитических функций
• Поток (математика)
• Тетрация
• Функциональное уравнение

Внешние ссылки

• Гилл, Джон (январь 2017 г.). «Букварь по элементарной теории бесконечных композиций комплексных функций» . Государственный университет Колорадо.