Тетрация

Не путать с титрованием .

О повторной тетрации см. Пентация .

Раскраска голоморфной тетрации доменов ${}^{z}e$, где оттенок функции представляет аргумент , а яркость представляет величину

${}^{n}x$, для n = 2, 3, 4, ... , демонстрирующий сходимость к бесконечно повторяемой экспоненте между двумя точками

В математике основанная тетрация (или гипер-4 ) — это операция, на итерированном или многократном возведении в степень . не существует Стандартного обозначения тетрации , хотя обозначение стрелки вверх Кнута $\uparrow \uparrow$ и левый показатель ^х б являются общими.

Согласно определению как повторное возведение в степень, ${^{n}a}$ означает ${a^{a^{\cdot ^{\cdot ^{a}}}}}$, где n копий a повторяются посредством возведения в степень справа налево, т. е. применения возведения в степень $n-1$ раз. n называется «высотой» функции, а a — «базой», аналогично возведению в степень. Это можно было бы прочитать как « энная тетрация » .

Это следующая гипероперация после возведения в степень , но перед пентацией . Слово было придумано Рубеном Луи Гудштейном из тетра- (четыре) и итерации .

Тетрация также определяется рекурсивно как

${a\uparrow \uparrow n}:={\begin{cases}1&{\text{if }}n=0,\\a^{a\uparrow \uparrow (n-1)}&{\text{if }}n>0,\end{cases}}$

позволяя предпринимать попытки распространить тетрацию на ненатуральные числа, такие как действительные и комплексные числа .

Две обратные тетрации называются суперкорнем и суперлогарифмом , аналогично корню n-й степени и логарифмическим функциям. Ни одна из трех функций не является элементарной .

Тетрация используется для обозначения очень больших чисел .

Введение

Здесь показаны первые четыре гипероперации , причем тетрация считается четвертой в серии. Последовательность унарных операций , определяемая как $a'=a+1$, считается нулевой операцией.

1. Добавление
   $$a+n=a+\underbrace {1+1+\cdots +1} _{n}$$
   n экземпляров по 1 добавлены к объединенному последовательно.
2. Умножение
   $$n\times a=\underbrace {a+a+\cdots +a} _{n}$$
   n экземпляров объединяются путем сложения .
3. Возведение в степень
   $$a^{n}=\underbrace {a\times a\times \cdots \times a} _{n}$$
   n экземпляров объединяются путем умножения.
4. Тетрация
   $${^{n}a}=\underbrace {a^{a^{\cdot ^{\cdot ^{a}}}}} _{n}$$
   n копий объединяются возведением в степень справа налево.

Обратите внимание, что вложенные показатели обычно интерпретируются сверху вниз: $a^{b^{c}}$ означает $a^{\left(b^{c}\right)}$ и не $\left(a^{b}\right)^{c}.$

Преемственность, $a_{n+1}=a_{n}+1$, — самая основная операция; при добавлении ( $a+n$) является основной операцией, для сложения натуральных чисел ее можно рассматривать как цепную последовательность $n$ преемники $a$; умножение ( $a\times n$) также является основной операцией, хотя для натуральных чисел ее аналогично можно рассматривать как цепное сложение, включающее $n$ количество $a$. Возведение в степень можно рассматривать как цепное умножение, включающее $n$ количество $a$ и тетрация ( $^{n}a$) как скованная сила, включающая $n$ цифры $a$. Каждая из вышеперечисленных операций определяется путем итерации предыдущей; однако, в отличие от предыдущих операций, тетрация не является элементарной функцией .

Параметр $a$ называется базовым , а параметр $n$ можно назвать высотой . В исходном определении тетрации параметр высоты должен быть натуральным числом; например, было бы нелогично сказать: «три возвели на себя отрицательно пять раз» или «четыре возвели на себя половину времени». Однако так же, как сложение, умножение и возведение в степень можно определить способами, допускающими расширение действительных и комплексных чисел, было предпринято несколько попыток обобщить тетрацию на отрицательные числа, действительные числа и комплексные числа. Один из таких способов сделать это — использовать рекурсивное определение тетрации; для любого положительного реального $a>0$ и неотрицательное целое число $n\geq 0$, мы можем определить $\,\!{^{n}a}$ рекурсивно как:

${^{n}a}:={\begin{cases}1&{\text{if }}n=0\\a^{\left(^{(n-1)}a\right)}&{\text{if }}n>0\end{cases}}$

Рекурсивное определение эквивалентно многократному возведению в степень натуральной высоты; однако это определение допускает расширение на другие высоты, такие как $^{0}a$, $^{-1}a$, и $^{i}a$ а также – многие из этих расширений являются областями активных исследований.

Терминология

Существует множество терминов для обозначения тетрации, каждый из которых имеет определенную логику, но некоторые из них по той или иной причине не стали широко использоваться. Вот сравнение каждого термина с его обоснованием и контробоснованием.

• Термин тетрация , введенный Гудштейном в его статье 1947 года «Трансфинитные ординалы в рекурсивной теории чисел». (обобщающее рекурсивное базовое представление, используемое в теореме Гудштейна, для использования операций более высокого уровня), получило доминирование. Оно также было популяризировано в книге Руди Ракера « Бесконечность и разум» .
• Термин «суперэкспоненциализация» был опубликован Бромером в его статье «Суперэкспоненциализация» в 1987 году. Ранее его использовал Эд Нельсон в своей книге «Предикативная арифметика», Princeton University Press, 1986.
• Термин «гипердержава» — это естественная комбинация слов «гипер» и «сила» , которая удачно описывает тетратацию. Проблема заключается в значении слова «гипер» по отношению к последовательности гиперопераций . При рассмотрении гиперопераций термин «гипер» относится ко всем рангам, а термин «супер» относится к 4-му рангу или тетрации. Таким образом, с учетом этих соображений гиперсила вводит в заблуждение, поскольку речь идет только о тетрации.
• Термин силовая башня иногда используется в форме «энергетическая башня порядка n » для ${\ \atop {\ }}{{\underbrace {a^{a^{\cdot ^{\cdot ^{a}}}}} } \atop n}$. Возведение в степень легко неверно истолковать: обратите внимание, что операция возведения в степень правоассоциативна (см. ниже ). Тетрация — это повторяющееся возведение в степень (назовем эту правоассоциативную операцию ^), начиная с верхней правой части выражения с экземпляра a^a (назовем это значение c). Возведение в степень следующего левого a (назовем это «следующим основанием» b) означает работу влево после получения нового значения b^c. Двигаясь влево, используйте следующий a слева как базовый b и оцените новый b^c. «Спуститься вниз по башне» по очереди, с новым большим значением c на следующем шаге вниз.

Частично из-за некоторой общей терминологии и схожей символики обозначений тетрацию часто путают с тесно связанными функциями и выражениями. Вот несколько связанных терминов:

Термины, связанные с тетрацией

Терминология	Форма
Тетрация	$a^{a^{\cdot ^{\cdot ^{a^{a}}}}}$
Итерированные экспоненты	$a^{a^{\cdot ^{\cdot ^{a^{x}}}}}$
Вложенные экспоненты (также башни)	$a_{1}^{a_{2}^{\cdot ^{\cdot ^{a_{n}}}}}$
Бесконечные экспоненты (также башни)	$a_{1}^{a_{2}^{a_{3}^{\cdot ^{\cdot ^{\cdot }}}}}$

В первых двух выражениях a — это основание , а количество раз, когда a появляется, — это высота (добавьте единицу вместо x ). В третьем выражении n — высота , но основания у всех разные.

Необходимо соблюдать осторожность при обращении к повторяющимся экспонентам, поскольку выражения этой формы принято называть повторным возведением в степень, что является неоднозначным, поскольку это может означать либо повторяющиеся степени , либо повторенные экспоненты .

Обозначения

Существует множество различных стилей обозначений, которые можно использовать для выражения тетрации. Некоторые обозначения также можно использовать для описания других гиперопераций , тогда как некоторые ограничиваются тетрацией и не имеют непосредственного расширения.

Стили обозначений для тетрации

Имя	Форма	Описание
Обозначения Руди Ракера	$\,{}^{n}a$	Используется Маурером [1901] и Гудстейном [1947]; Руди Ракера « Книга Бесконечность и разум» популяризировала эту систему обозначений.
Обозначение Кнута со стрелкой вверх	${\begin{aligned}a{\uparrow \uparrow }n\\a{\uparrow }^{2}n\end{aligned}}$	Позволяет расширять, добавляя больше стрелок или, что еще более эффективно, индексированную стрелку.
Обозначение цепной стрелки Конвея	$a\rightarrow n\rightarrow 2$	Позволяет расширять за счет увеличения числа 2 (эквивалентно расширениям, указанным выше), а также, что еще более эффективно, за счет расширения цепочки.
функция Аккермана	${}^{n}2=\operatorname {A} (4,n-3)+3$	Допускает особый случай $a=2$ записать через функцию Аккермана.
Итерированная экспоненциальная запись	$\exp _{a}^{n}(1)$	Позволяет простое расширение итерированных экспонент от начальных значений, отличных от 1.
Обозначения Хушмана	${\begin{aligned}&\operatorname {uxp} _{a}n\\[2pt]&a^{\frac {n}{}}\end{aligned}}$	Используется М. Х. Хушмандом [2006].
гиперопераций Обозначения	${\begin{aligned}&a[4]n\\[2pt]&H_{4}(a,n)\end{aligned}}$	Позволяет расширение путем увеличения числа 4; это дает семейство гиперопераций .
Обозначение двойной каретки	a^^n	Поскольку стрелка вверх используется идентично курсору ( ^), тетрацию можно записать как ( ^^); удобно для ASCII .

В одном из приведенных выше обозначений используется итерированная экспоненциальная запись; в целом это определяется следующим образом:

$\exp _{a}^{n}(x)=a^{a^{\cdot ^{\cdot ^{a^{x}}}}}$ с н а с.

Обозначений для повторяющихся экспонент не так много, но вот некоторые из них:

Стили обозначений для повторяющихся экспонент

Имя	Форма	Описание
Стандартные обозначения	$\exp _{a}^{n}(x)$	Эйлер ввёл обозначение $\exp _{a}(x)=a^{x}$и обозначение итерации $f^{n}(x)$ существует примерно столько же времени.
Обозначение Кнута со стрелкой вверх	$(a{\uparrow }^{2}(x))$	Позволяет использовать сверхспособности и суперэкспоненциальную функцию за счет увеличения количества стрелок; используется в статье о больших числах .
Текстовые обозначения	exp_a^n(x)	На основе стандартных обозначений; удобно для ASCII .
J-обозначение	x^^:(n-1)x	Повторяет возведение в степень. См . J (язык программирования).
Обозначение бесконечного барьера	$a\uparrow \uparrow n|x$	Джонатан Бауэрс придумал это: и его можно распространить на более высокие гипероперации

Примеры

Из-за чрезвычайно быстрого роста тетрации большинство значений в следующей таблице слишком велики, чтобы их можно было записать в экспоненциальном представлении. В этих случаях для их выражения в десятичной системе используется итерированная экспоненциальная запись. Значения, содержащие десятичную точку, являются приблизительными.

Примеры тетрации

$x$	${}^{2}x$	${}^{3}x$	${}^{4}x$	${}^{5}x$	${}^{6}x$	${}^{7}x$
1	1	1	1	1	1	1
2	4 (2 2 )	16 (2 4 )	65,536 (2 16 )	2.00353 × 10 19,728	$\exp _{10}^{3}(4.29508)$ (10 6.03123×10 19,727 )	$\exp _{10}^{4}(4.29508)$ (10 10 6.03123×10 19,727 )
3	27 (3 3 )	7,625,597,484,987 (3 27 )	$\exp _{10}^{3}(1.09902)$ (1.25801 × 10 3,638,334,640,024 )	$\exp _{10}^{4}(1.09902)$	$\exp _{10}^{5}(1.09902)$	$\exp _{10}^{6}(1.09902)$
4	256 (4 4 )	1.34078 × 10 154 (4 256 )	$\exp _{10}^{3}(2.18726)$ (10 8.0723×10 153 )	$\exp _{10}^{4}(2.18726)$	$\exp _{10}^{5}(2.18726)$	$\exp _{10}^{6}(2.18726)$
5	3,125 (5 5 )	1.91101 × 10 2,184 (5 3,125 )	$\exp _{10}^{3}(3.33928)$ (10 1.33574×10 2,184 )	$\exp _{10}^{4}(3.33928)$	$\exp _{10}^{5}(3.33928)$	$\exp _{10}^{6}(3.33928)$
6	46,656 (6 6 )	2.65912 × 10 36,305 (6 46,656 )	$\exp _{10}^{3}(4.55997)$ (10 2.0692×10 36,305 )	$\exp _{10}^{4}(4.55997)$	$\exp _{10}^{5}(4.55997)$	$\exp _{10}^{6}(4.55997)$
7	823,543 (7 7 )	3.75982 × 10 695,974 (7 823,543 )	$\exp _{10}^{3}(5.84259)$ (3.17742 × 10 695,974 цифры)	$\exp _{10}^{4}(5.84259)$	$\exp _{10}^{5}(5.84259)$	$\exp _{10}^{6}(5.84259)$
8	16,777,216 (8 8 )	6.01452 × 10 15,151,335	$\exp _{10}^{3}(7.18045)$ (5.43165 × 10 15,151,335 цифры)	$\exp _{10}^{4}(7.18045)$	$\exp _{10}^{5}(7.18045)$	$\exp _{10}^{6}(7.18045)$
9	387,420,489 (9 9 )	4.28125 × 10 369,693,099	$\exp _{10}^{3}(8.56784)$ (4.08535 × 10 369,693,099 цифры)	$\exp _{10}^{4}(8.56784)$	$\exp _{10}^{5}(8.56784)$	$\exp _{10}^{6}(8.56784)$
10	10,000,000,000 (10 10 )	10 10,000,000,000	$\exp _{10}^{3}(10)$ (10 10,000,000,000 + 1 цифра)	$\exp _{10}^{4}(10)$	$\exp _{10}^{5}(10)$	$\exp _{10}^{6}(10)$

Замечание: Если х не отличается от 10 на порядки, то для всех $k\geq 3,~^{m}x=\exp _{10}^{k}z,~z>1~\Rightarrow ~^{m+1}x=\exp _{10}^{k+1}z'{\text{ with }}z'\approx z$. Например, $z-z'<1.5\cdot 10^{-15}{\text{ for }}x=3=k,~m=4$ в приведенной выше таблице, а в следующих строках разница еще меньше.

Расширения

Тетрацию можно расширить двумя разными способами; в уравнении $^{n}a\!$, как основание a , так и высоту n можно обобщить, используя определение и свойства тетрации. Хотя основание и высота могут быть расширены за пределы неотрицательных целых чисел на разные домены , включая ${^{n}0}$, сложные функции, такие как ${}^{n}i$и высоты бесконечного n , более ограниченные свойства тетрации уменьшают способность расширять тетратацию.

Расширение домена для баз

Базовый ноль

Экспоненциальная $0^{0}$ не определяется однозначно. Таким образом, тетрации $\,{^{n}0}$ не определены четко формулой, приведенной ранее. Однако, $\lim _{x\rightarrow 0}{}^{n}x$ четко определен и существует:

$\lim _{x\rightarrow 0}{}^{n}x={\begin{cases}1,&n{\text{ even}}\\0,&n{\text{ odd}}\end{cases}}$

Таким образом, мы могли последовательно определить ${}^{n}0=\lim _{x\rightarrow 0}{}^{n}x$. Это аналогично определению $0^{0}=1$.

В рамках этого расширения ${}^{0}0=1$, поэтому правило ${^{0}a}=1$ исходное определение все еще остается в силе.

Сложные базы

Тетрация по периоду

Тетрация побегом

Поскольку комплексные числа можно возводить в степени, тетрацию можно применять к основаниям вида z = a + bi (где a и b вещественные). Например, в ^н z при z = i тетратирование достигается за счет использования главной ветви натурального логарифма; используя формулу Эйлера, получаем соотношение:

$i^{a+bi}=e^{{\frac {1}{2}}{\pi i}(a+bi)}=e^{-{\frac {1}{2}}{\pi b}}\left(\cos {\frac {\pi a}{2}}+i\sin {\frac {\pi a}{2}}\right)$

Это предполагает рекурсивное определение для ^{п +1} i = a' + b'i при любом ^н я = а + би :

${\begin{aligned}a'&=e^{-{\frac {1}{2}}{\pi b}}\cos {\frac {\pi a}{2}}\\[2pt]b'&=e^{-{\frac {1}{2}}{\pi b}}\sin {\frac {\pi a}{2}}\end{aligned}}$

Можно получить следующие приблизительные значения:

Значения тетрации комплексных оснований

${\textstyle {}^{n}i}$	Приблизительная стоимость
${\textstyle {}^{1}i=i}$	я
${\textstyle {}^{2}i=i^{\left({}^{1}i\right)}}$	0.2079
${\textstyle {}^{3}i=i^{\left({}^{2}i\right)}}$	0,9472 + 0,3208 я
${\textstyle {}^{4}i=i^{\left({}^{3}i\right)}}$	0,0501 + 0,6021 я
${\textstyle {}^{5}i=i^{\left({}^{4}i\right)}}$	0,3872 + 0,0305 я
${\textstyle {}^{6}i=i^{\left({}^{5}i\right)}}$	0,7823 + 0,5446 я
${\textstyle {}^{7}i=i^{\left({}^{6}i\right)}}$	0,1426 + 0,4005 я
${\textstyle {}^{8}i=i^{\left({}^{7}i\right)}}$	0,5198 + 0,1184 я
${\textstyle {}^{9}i=i^{\left({}^{8}i\right)}}$	0,5686 + 0,6051 я

Решение обратной зависимости, как и в предыдущем разделе, дает ожидаемое ⁰ я = 1 и ⁻¹ i = 0 , с отрицательными значениями n, дающими бесконечные результаты на мнимой оси. На комплексной плоскости вся последовательность движется по спирали до предела 0,4383 + 0,3606 i , что можно интерпретировать как значение, при котором n бесконечно.

Такие последовательности тетрации изучаются со времен Эйлера, но мало изучены из-за их хаотичного поведения. Большинство опубликованных исследований исторически были сосредоточены на сходимости бесконечно повторяемой экспоненциальной функции. Текущим исследованиям во многом способствовало появление мощных компьютеров с программным обеспечением для фрактальной и символьной математики. Многое из того, что известно о тетрации, основано на общих знаниях о сложной динамике и конкретных исследованиях экспоненциальной карты.

Расширения домена на разную высоту

Бесконечная высота

$\textstyle \lim _{n\rightarrow \infty }{}^{n}x$ бесконечно повторяемой экспоненты сходится для базисов $\textstyle \left(e^{-1}\right)^{e}\leq x\leq e^{\left(e^{-1}\right)}$

Функция $\left|{\frac {\mathrm {W} (-\ln {z})}{-\ln {z}}}\right|$ на комплексной плоскости, показывающая действительную бесконечно повторяемую экспоненциальную функцию (черная кривая)

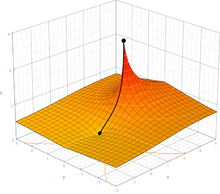
Тетрацию можно расширить до бесконечных высот; т.е. для определенных значений a и n в ${}^{n}a$, существует четко определенный результат для бесконечного n . Это связано с тем, что для оснований внутри определенного интервала тетрация сходится к конечному значению при стремлении высоты к бесконечности . Например, ${\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{\cdot ^{\cdot ^{\cdot }}}}}$ сходится к 2, и поэтому можно сказать, что оно равно 2. Тенденцию к 2 можно увидеть, оценив небольшую конечную башню:

${\begin{aligned}{\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{1.414}}}}}&\approx {\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{1.63}}}}\\&\approx {\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{1.76}}}\\&\approx {\sqrt {2}}^{{\sqrt {2}}^{1.84}}\\&\approx {\sqrt {2}}^{1.89}\\&\approx 1.93\end{aligned}}$

В общем, бесконечно повторяемая экспонента $x^{x^{\cdot ^{\cdot ^{\cdot }}}}\!\!$, определяемый как предел ${}^{n}x$ когда n стремится к бесконечности, сходится для e ^{− и} ≤ х ≤ е ^{1/ и} , примерно интервал от 0,066 до 1,44, результат, показанный Леонардом Эйлером . Предел, если он существует, является положительным вещественным решением уравнения y = x ^и . Таким образом, x = y ^{1/ и} . Предел, определяющий бесконечную экспоненту от x, не существует, когда x > e ^{1/ и} потому что максимум y ^{1/ и} это е ^{1/ и} . Предел также не существует, когда 0 < x < e ^{− и} .

Это можно распространить на комплексные числа z с помощью определения:

${}^{\infty }z=z^{z^{\cdot ^{\cdot ^{\cdot }}}}={\frac {\mathrm {W} (-\ln {z})}{-\ln {z}}}~,$

где W представляет собой W-функцию Ламберта .

Поскольку предел y = ^∞ x (если он существует на положительной вещественной линии, т.е. для e ^{− и} ≤ х ≤ е ^{1/ и} ) должно удовлетворять x ^и = y мы видим, что x ↦ y = ^∞ x — (нижняя ветвь) обратная функция y ↦ x = y ^{1/ и} .

Отрицательные высоты

Мы можем использовать рекурсивное правило для тетрации:

${^{k+1}a}=a^{\left({^{k}a}\right)},$

доказать ${}^{-1}a$:

$^{k}a=\log _{a}\left(^{k+1}a\right);$

на −1 Замена k дает

${}^{-1}a=\log _{a}\left({}^{0}a\right)=\log _{a}1=0$.

Меньшие отрицательные значения не могут быть точно определены таким способом. Подстановка -2 вместо k в том же уравнении дает

${}^{-2}a=\log _{a}\left({}^{-1}a\right)=\log _{a}0=-\infty$

который не совсем определен. Однако иногда их можно считать наборами.

Для $n=1$, любое определение $\,\!{^{-1}1}$ соответствует правилу, поскольку

${^{0}1}=1=1^{n}$ для любого $\,\!n={^{-1}1}$.

Реальные высоты

В настоящее время не существует общепринятого решения общей проблемы распространения тетрации на действительные или комплексные значения n . Однако существует множество подходов к этому вопросу, и различные подходы изложены ниже.

В общем, проблема состоит в том, чтобы для любого действительного a > 0 найти суперэкспоненциальную функцию. $\,f(x)={}^{x}a$ по вещественному x > −2, что удовлетворяет

• $\,{}^{-1}a=0$
• $\,{}^{0}a=1$
• $\,{}^{x}a=a^{\left({}^{x-1}a\right)}$для всех реально $x>-1.$

Чтобы найти более естественное расширение, обычно требуется одно или несколько дополнительных требований. Обычно это набор из следующего:

• Требование непрерывности (обычно именно это) ${}^{x}a$ непрерывен по обеим переменным для $x>0$).
• Требование дифференцируемости (может быть один, два, k раз или бесконечно дифференцируемым по x ).
• Требование регулярности ) , (подразумевающее дважды дифференцируемость по x которое:

  $\left({\frac {d^{2}}{dx^{2}}}f(x)>0\right)$ для всех $x>0$

Четвертое требование различается от автора к автору и в разных подходах. Существует два основных подхода к расширению тетрации до реальных высот; один основан на требовании регулярности , а другой — на требовании дифференцируемости . Эти два подхода кажутся настолько разными, что их невозможно согласовать, поскольку они дают несовместимые друг с другом результаты.

Когда $\,{}^{x}a$ определена для интервала длины один, вся функция легко следует для всех x > −2 .

реальных

$\,{}^{x}e$ используя линейное приближение

Линейная аппроксимация (решение требования непрерывности, приближение требования дифференцируемости) определяется выражением:

${}^{x}a\approx {\begin{cases}\log _{a}\left(^{x+1}a\right)&x\leq -1\\1+x&-1<x\leq 0\\a^{\left(^{x-1}a\right)}&0<x\end{cases}}$

следовательно:

Значения линейной аппроксимации

Приближение	Домен
${\textstyle {}^{x}a\approx x+1}$	для −1 < x < 0
${\textstyle {}^{x}a\approx a^{x}}$	для 0 < х < 1
${\textstyle {}^{x}a\approx a^{a^{(x-1)}}}$	для 1 < х < 2

и так далее. Однако он дифференцируем только кусочно; при целых значениях x производная умножается на $\ln {a}$. Оно непрерывно дифференцируемо для $x>-2$ тогда и только тогда, когда $a=e$. Например, используя эти методы ${}^{\frac {\pi }{2}}e\approx 5.868...$ и ${}^{-4.3}0.5\approx 4.03335...$

Основная теорема статьи Хушманда. утверждает: Пусть $0<a\neq 1$. Если $f:(-2,+\infty )\rightarrow \mathbb {R}$ является непрерывным и удовлетворяет условиям:

• $f(x)=a^{f(x-1)}\;\;{\text{for all}}\;\;x>-1,\;f(0)=1,$
• $f$ дифференцируема на (−1, 0) ,
• $f^{\prime }$ — неубывающая или невозрастающая функция на (−1, 0) ,
• $f^{\prime }\left(0^{+}\right)=(\ln a)f^{\prime }\left(0^{-}\right){\text{ or }}f^{\prime }\left(-1^{+}\right)=f^{\prime }\left(0^{-}\right).$

затем $f$ однозначно определяется уравнением

$f(x)=\exp _{a}^{[x]}\left(a^{(x)}\right)=\exp _{a}^{[x+1]}((x))\quad {\text{for all}}\;\;x>-2,$

где $(x)=x-[x]$ обозначает дробную часть x и $\exp _{a}^{[x]}$ это $[x]$- итерированная функция функции $\exp _{a}$.

Доказательство состоит в том, что из условий со второго по четвертое тривиально следует, что f — линейная функция на [−1, 0] .

Линейное приближение к естественной тетратионной функции ${}^{x}e$ непрерывно дифференцируема, но ее вторая производная не существует при целых значениях аргумента. Хушманд вывел для него еще одну теорему единственности, которая гласит:

Если $f:(-2,+\infty )\rightarrow \mathbb {R}$ является непрерывной функцией, которая удовлетворяет:

• $f(x)=e^{f(x-1)}\;\;{\text{for all}}\;\;x>-1,\;f(0)=1,$
• $f$ выпукла на (−1, 0) ,
• $f^{\prime }\left(0^{-}\right)\leq f^{\prime }\left(0^{+}\right).$

затем $f={\text{uxp}}$. [Здесь $f={\text{uxp}}$ это название Хушманда для линейного приближения к естественной функции тетрации.]

Доказательство во многом такое же, как и раньше; уравнение рекурсии гарантирует, что $f^{\prime }(-1^{+})=f^{\prime }(0^{+}),$ и тогда из условия выпуклости следует, что $f$ линейна на (−1, 0) .

Поэтому линейное приближение к естественной тетрации является единственным решением уравнения $f(x)=e^{f(x-1)}\;\;(x>-1)$ и $f(0)=1$ которая выпукла на (−1, +∞) . Все остальные достаточно дифференцируемые решения должны иметь точку перегиба на интервале (−1, 0) .

порядка для реальных

Сравнение линейного и квадратичного приближений (красным и синим соответственно) функции $^{x}0.5$, от x = −2 до x = 2

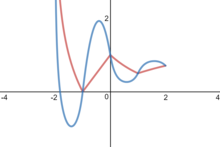
Помимо линейных приближений, квадратичная аппроксимация (требования дифференцируемости) определяется формулой:

${}^{x}a\approx {\begin{cases}\log _{a}\left({}^{x+1}a\right)&x\leq -1\\1+{\frac {2\ln(a)}{1\;+\;\ln(a)}}x-{\frac {1\;-\;\ln(a)}{1\;+\;\ln(a)}}x^{2}&-1<x\leq 0\\a^{\left({}^{x-1}a\right)}&x>0\end{cases}}$

который является дифференцируемым для всех $x>0$, но не дважды дифференцируема. Например, ${}^{\frac {1}{2}}2\approx 1.45933...$ Если $a=e$ это то же самое, что и линейное приближение.

Из-за способа расчета эта функция не «отменяется», в отличие от показателей степени, где $\left(a^{\frac {1}{n}}\right)^{n}=a$. А именно,

${}^{n}\left({}^{\frac {1}{n}}a\right)=\underbrace {\left({}^{\frac {1}{n}}a\right)^{\left({}^{\frac {1}{n}}a\right)^{\cdot ^{\cdot ^{\cdot ^{\cdot ^{\left({}^{\frac {1}{n}}a\right)}}}}}}} _{n}\neq a$.

Подобно квадратичному приближению существуют и кубические приближения и методы обобщения на приближения степени п , хотя они гораздо более громоздки.

Комплексные высоты

Чертеж аналитического расширения $f=F(x+{\rm {i}}y)$ тетрации в комплексную плоскость. Уровни $|f|=1,e^{\pm 1},e^{\pm 2},\ldots$ и уровни $\arg(f)=0,\pm 1,\pm 2,\ldots$ показаны толстыми кривыми.

В 2017 году было доказано что существует единственная функция F , которая является решением уравнения F ( z + 1) = exp( F ( z )) и удовлетворяет дополнительным условиям, что F (0) = 1 и F ( z ) приближается к точкам неподвижным логарифм (примерно ± 1,337 i ) при z приближении к ± i ∞ и что F голоморфен 0,318 во всей комплексной z -плоскости, за исключением части вещественной оси при z ≤ −2 . Это доказательство подтверждает предыдущую гипотезу . Построение такой функции было первоначально продемонстрировано Кнезером в 1950 году. Комплексная карта этой функции показана на рисунке справа. Доказательство также работает для других оснований, кроме e , если база больше, чем $e^{\frac {1}{e}}\approx 1.445$. Последующие работы распространили строительство на все базы комплекса.

Требование голоморфности тетрации важно для ее единственности. Многие функции S можно построить как

$S(z)=F\!\left(~z~+\sum _{n=1}^{\infty }\sin(2\pi nz)~\alpha _{n}+\sum _{n=1}^{\infty }{\Big (}1-\cos(2\pi nz){\Big )}~\beta _{n}\right)$

где α и β — вещественные последовательности, которые затухают достаточно быстро, чтобы обеспечить сходимость ряда , по крайней мере, при умеренных значениях Im z .

Функция S удовлетворяет уравнениям тетрации S ( z + 1) = exp( S ( z )) , S (0) = 1 , и если α _n и β _n приближаются к 0 достаточно быстро, она будет аналитической в ​​окрестности положительной точки. реальная ось. Однако если некоторые элементы { α } или { β } не равны нулю, то функция S имеет множество дополнительных особенностей и порезов на комплексной плоскости из-за экспоненциального роста sin и cos вдоль мнимой оси; чем меньше коэффициенты { α } и { β } , тем дальше эти особенности находятся от вещественной оси.

Таким образом, расширение тетрации на комплексную плоскость существенно для уникальности; вещественно -аналитическая тетрация не единственна.

Неэлементарная рекурсивность

Тетрация (ограничена $\mathbb {N} ^{2}$) не является элементарной рекурсивной функцией . По индукции можно доказать, что для каждой элементарной рекурсивной функции f существует константа c такая, что

$f(x)\leq \underbrace {2^{2^{\cdot ^{\cdot ^{x}}}}} _{c}.$

Обозначим правую часть через $g(c,x)$. Предположим противное, что тетрация элементарно рекурсивна. $g(x,x)+1$ также является элементарно рекурсивным. Согласно приведенному выше неравенству существует константа c такая, что $g(x,x)+1\leq g(c,x)$. Позволяя $x=c$, у нас это есть $g(c,c)+1\leq g(c,c)$, противоречие.

Обратные операции

Возведение в степень имеет две обратные операции; корни и логарифмы . Аналогично, обратные тетрации часто называют суперкорнем и суперлогарифмом ( фактически, все гипероперации, большие или равные 3, имеют аналогичные обратные); например, в функции ${^{3}}y=x$, двумя обратными являются суперкорень куба и основание суперлогарифма y x y .

Суперкорень

«Суперкорень» перенаправляется сюда. Чтобы узнать о каталоге, поддерживаемом некоторыми Unix-системами, см. super-root (computing) .

Суперкорень — это обратная операция тетрации по отношению к основанию: если $^{n}y=x$, то y является n- м суперкорнем из x ( ${\sqrt[{n}]{x}}_{s}$ или ${\sqrt[{4}]{x}}_{s}$).

Например,

$^{4}2=2^{2^{2^{2}}}=65{,}536$

таким образом, 2 — это четвертый суперкорень из 65 536.

Квадратный суперкорень

График $y={\sqrt {x}}_{s}$

Суперкорень 2-го порядка , квадратный суперкорень или суперквадратный корень имеют два эквивалентных обозначения: $\mathrm {ssrt} (x)$ и ${\sqrt {x}}_{s}$. Это инверсия $^{2}x=x^{x}$ и может быть представлен функцией Ламберта W :

$\mathrm {ssrt} (x)=e^{W(\ln x)}={\frac {\ln x}{W(\ln x)}}$

Функция также иллюстрирует отражающую природу функций корня и логарифма, поскольку приведенное ниже уравнение справедливо только тогда, когда $y=\mathrm {ssrt} (x)$:

${\sqrt[{y}]{x}}=\log _{y}x$

Как и квадратные корни , квадратный суперкорень из x может не иметь единственного решения. В отличие от квадратных корней, определение количества квадратных суперкорней из x может оказаться затруднительным. В общем, если $e^{-1/e}<x<1$, то x имеет два положительных квадратных суперкорня между 0 и 1; и если $x>1$, то x имеет один положительный квадратный суперкорень, больший 1. Если x положителен и меньше $e^{-1/e}$ у него нет действительных квадратных суперкорней, но приведенная выше формула дает счетное бесконечное число комплексных корней для любого конечного x, не равного 1. Функция использовалась для определения размера кластеров данных .

В $x=1$:

$$\mathrm {ssrt} (x)=1+(x-1)-(x-1)^{2}+{\frac {3}{2}}(x-1)^{3}-{\frac {17}{6}}(x-1)^{4}+{\frac {37}{6}}(x-1)^{5}-{\frac {1759}{120}}(x-1)^{6}+{\frac {13279}{360}}(x-1)^{7}+{\mathcal {O}}{\left((x-1)^{8}\right)}$$

Другие суперкорни

График $y={\sqrt[{3}]{x}}_{s}$

Для каждого целого числа n > 2 функция ^н x определен и увеличивается при x ≥ 1 , и ^н 1 = 1 , так что n -й суперкорень x , ${\sqrt[{n}]{x}}_{s}$, существует для x ≥ 1 .

Одной из более простых и быстрых формул суперкорня третьей степени является рекурсивная формула, если: x ^{х х} = a , а затем x ( n + 1) = exp (W (W ( x ( n ) ln ( a )))) , например x (0) = 1 .

Однако если линейное приближение, указанное выше , то используется $^{y}x=y+1$ если −1 < y ≤ 0 , поэтому $^{y}{\sqrt {y+1}}_{s}$ не может существовать.

Так же, как и для квадратного суперкорня, терминология для других суперкорней может быть основана на нормальных корнях : «кубические суперкорни» можно выразить как ${\sqrt[{3}]{x}}_{s}$; «4-й суперкорень» можно выразить как ${\sqrt[{4}]{x}}_{s}$; и « n -й суперкорень» равен ${\sqrt[{n}]{x}}_{s}$. Обратите внимание, что ${\sqrt[{n}]{x}}_{s}$ не может быть определен однозначно, поскольку может быть более одного n ^й корень. Например, x имеет один (действительный) суперкорень, если , и n нечетное до двух, n четное если .

Как и в случае с расширением тетрации на бесконечные высоты, суперкорень можно расширить до n = ∞ , и он корректно определен, если 1/ e ≤ x ≤ e . Обратите внимание, что $x={^{\infty }y}=y^{\left[^{\infty }y\right]}=y^{x},$ и таким образом, что $y=x^{1/x}$. Поэтому, когда оно четко определено, ${\sqrt[{\infty }]{x}}_{s}=x^{1/x}$ и, в отличие от обычной тетрации, является элементарной функцией . Например, ${\sqrt[{\infty }]{2}}_{s}=2^{1/2}={\sqrt {2}}$.

следует Из теоремы Гельфонда–Шнайдера , что суперкорень ${\sqrt {n}}_{s}$ для любого положительного целого числа n является либо целым, либо трансцендентным , и ${\sqrt[{3}]{n}}_{s}$ либо целое, либо иррациональное. Вопрос о том, являются ли иррациональные сверхкорни трансцендентными в последнем случае, остается открытым.

Суперлогарифм

Основная статья: Суперлогарифм

Как только непрерывное возрастающее (по x ) определение тетрации, ^х a , выбран соответствующий суперлогарифм $\operatorname {slog} _{a}x$ или $\log _{a}^{4}x$ определяется для всех действительных чисел x и a > 1 .

Функция slog _a   x удовлетворяет:

${\begin{aligned}\operatorname {slog} _{a}{^{x}a}&=x\\\operatorname {slog} _{a}a^{x}&=1+\operatorname {slog} _{a}x\\\operatorname {slog} _{a}x&=1+\operatorname {slog} _{a}\log _{a}x\\\operatorname {slog} _{a}x&\geq -2\end{aligned}}$

Открытые вопросы

Помимо проблем с расширениями тетрации, существует несколько открытых вопросов, касающихся тетрации, особенно когда речь идет об отношениях между системами счисления, такими как целые и иррациональные числа :

• Неизвестно, существует ли целое положительное число n, для которого ^н π или ^н е — целое число. В частности, неизвестно, является ли кто-либо из ⁴ π или ⁵ е — целое число.
• Неизвестно, является ли ^н q является рациональным для любого положительного целого числа n и положительного нецелого рационального q . Например, неизвестно, имеет ли положительный корень уравнения ⁴ x = 2 — рациональное число.
• Неизвестно, является ли ^и π или ^п Являемся ли мы рациональными или нет.

См. также

• функция Аккермана
• Обозначение большого О
• Двойная экспоненциальная функция
• Гипероперация
• Повторный логарифм
• Симметричная арифметика индекса уровня

Ссылки

• Дэниел Гейслер, Тетрация
• Иоаннис Галидакис, О расширении Hyper4 до нецелых чисел (без даты, 2006 г. или ранее) (более простой и легкий для чтения обзор следующей ссылки)
• Иоаннис Галидакис, О распространении гипер4 и нотации Кнута со стрелкой вверх на действительные числа (без даты, 2006 г. или ранее).
• Роберт Мунафо, Расширение функции Hyper4 на действительные числа (неформальное обсуждение распространения тетрации на действительные числа).
• Лоде Вандевенн, Тетрация квадратного корня из двух . (2004). (Попытайтесь распространить тетрацию на действительные числа.)
• Иоаннис Галидакис, Математика , (Окончательный список ссылок на исследования тетрации. Много информации о W-функции Ламберта, римановых поверхностях и аналитическом продолжении.)
• Джозеф МакДонелл, Некоторые критические точки функции сверхмощности .
• Дэйв Л. Ренфро, Веб-страницы для бесконечно повторяющихся экспонент
• Кнобель, Р. (1981). «Экспонента повторяется». Американский математический ежемесячник . 88 (4): 235–252. дои : 10.1080/00029890.1981.11995239 .
• Ганс Маурер, «О функции $y=x^{[x^{[x(\cdots )]}]}$ для целочисленного аргумента (обилия)». Сообщения Математического общества в Гамбурге 4 , (1901), стр. 33–50. (Ссылка на использование $\ {^{n}a}$ из статьи Кнобеля.)
• Четвертая операция
• Лука Морони, Странные свойства бесконечной энергетической башни ( https://arxiv.org/abs/1908.05559 )

Дальнейшее чтение

• Галидакис, Иоаннис; Вайсштейн, Эрик Вольфганг . «Энергетическая башня» . Математический мир . Проверено 5 июля 2019 г.