Теорема Тейлора
| Часть серии статей о |
| Исчисление |
|---|
В исчислении дает теорема Тейлора приближение -раз дифференцируемая функция вокруг заданной точки по многочлену степени , называемый -го порядка Полином Тейлора . Для гладкой функции полином Тейлора представляет собой усечение порядка ряда Тейлора функции. Полином Тейлора первого порядка представляет собой линейное приближение функции, а полином Тейлора второго порядка часто называют квадратичным приближением . [1] Существует несколько версий теоремы Тейлора, некоторые из которых дают явные оценки ошибки аппроксимации функции ее полиномом Тейлора.
Теорема Тейлора названа в честь математика Брука Тейлора , который изложил ее версию в 1715 году. [2] хотя более ранняя версия результата уже упоминалась в 1671 году Джеймсом Грегори . [3]
Теорема Тейлора преподается на вводных курсах исчисления и является одним из центральных элементарных инструментов математического анализа . Он дает простые арифметические формулы для точного вычисления значений многих трансцендентных функций, таких как показательная функция и тригонометрические функции .Это отправная точка изучения аналитических функций и имеет фундаментальное значение в различных областях математики, а также в численном анализе и математической физике . Теорема Тейлора также распространяется на многомерные и векторные функции. Он обеспечил математическую основу для некоторых знаковых ранних вычислительных машин: Чарльза Бэббиджа вычисляла разностная машина синусы, косинусы, логарифмы и другие трансцендентные функции путем численного интегрирования первых семи членов их ряда Тейлора.
Мотивация
[ редактировать ]
Если вещественная функция дифференцируема в точке , то оно имеет линейное приближение вблизи этой точки . Это означает, что существует функция h 1 ( x ) такая, что
Здесь
является линейным приближением для x вблизи точки a , график которой это касательная к графику в х = а . Ошибка в приближении:
Поскольку x стремится к a, эта ошибка стремится к нулю гораздо быстрее, чем , изготовление полезное приближение.

Для лучшего приближения к , мы можем подогнать квадратичный многочлен вместо линейной функции:
Вместо того, чтобы просто сопоставлять одну производную в , этот полином имеет одинаковые первую и вторую производные, что видно при дифференцировании.
Теорема Тейлора гарантирует, что квадратичное приближение находится в достаточно малой окрестности , более точное, чем линейное приближение. Конкретно,
Здесь ошибка приближения равна
что, учитывая предельное поведение , стремится к нулю быстрее, чем поскольку x стремится к a .

Точно так же мы могли бы получить еще лучшие приближения к f, если бы использовали полиномы более высокой степени, поскольку тогда мы можем сопоставить еще больше производных с f в выбранной базовой точке.
В общем случае ошибка приближения функции многочленом степени k будет стремиться к нулю гораздо быстрее, чем поскольку x стремится к a . Однако существуют функции, даже бесконечно дифференцируемые, для которых увеличение степени аппроксимирующего полинома не увеличивает точность аппроксимации: мы говорим, что такая функция не может быть аналитической при x = a : она не определяется (локально) выражением его производные на данный момент.
Теорема Тейлора имеет асимптотический характер: она лишь говорит нам, что ошибка в приближении -го порядка Полином Тейлора P k стремится к нулю быстрее, чем любой ненулевой -й степени Полином как . Он не говорит нам, насколько велика ошибка в какой-либо конкретной окрестности центра расширения, но для этой цели существуют явные формулы для остаточного члена (приведенные ниже), которые справедливы при некоторых дополнительных предположениях о регулярности f . Эти расширенные версии теоремы Тейлора обычно приводят к равномерным оценкам ошибки аппроксимации в небольшой окрестности центра расширения, но эти оценки не обязательно выполняются для слишком больших окрестностей, даже если функция f является аналитической . В этой ситуации, возможно, придется выбрать несколько полиномов Тейлора с разными центрами разложения, чтобы получить надежные аппроксимации Тейлора исходной функции (см. анимацию справа).
Остаток можно использовать несколькими способами:
- Оцените ошибку для полинома P k ( x ) степени k, оценивающего на заданном интервале ( a – r , a + r ). (Учитывая интервал и степень, мы находим ошибку.)
- Найдите наименьшую степень k, для которой полином P k ( x ) приближается с точностью до заданной погрешности на заданном интервале ( a − r , a + r ) . (По интервалу и допуску на ошибку находим степень.)
- Найдите наибольший интервал ( a − r , a + r ), на котором P k ( x ) приближается с точностью до заданной погрешности. (По степени и допуску ошибок находим интервал.)
Теорема Тейлора об одной действительной переменной
[ редактировать ]Формулировка теоремы
[ редактировать ]Точная формулировка самой основной версии теоремы Тейлора выглядит следующим образом:
Теорема Тейлора [4] [5] [6] — Пусть k ≥ 1 — целое и пусть f : R → R дифференцируема k раз в R. точке a ∈ функция число Тогда существует функция hk что : R → R такая,
и Это называется формой Пеано остатка .
Полином, фигурирующий в теореме Тейлора, — это Полином Тейлора -го порядка
функции f в точке a . Полином Тейлора — это уникальный полином «асимптотического наилучшего соответствия» в том смысле, что если существует функция h k : R → R и -го порядка полином p такой, что
тогда р = Pk . Теорема Тейлора описывает асимптотическое поведение остаточного члена
что является ошибкой аппроксимации при аппроксимации f полиномом Тейлора. Используя обозначение «маленькое о» , утверждение в теореме Тейлора читается как
Явные формулы остатка
[ редактировать ]При более строгих предположениях о регулярности f существует несколько точных формул для остаточного члена R k полинома Тейлора, наиболее распространенными из которых являются следующие.
Формы среднего значения остатка . Пусть f : R → R будет k + 1 раз дифференцируемым на открытом интервале с f ( к ) непрерывен на замкнутом интервале между и . [7] Затем
для некоторого действительного числа между и . Это Лагранжа форма [8] остатка.
Сходным образом,
для некоторого действительного числа между и . Это Коши форма [9] остатка.
Оба можно рассматривать как частные случаи следующего результата:
для некоторого действительного числа между и . Это Шлёмильха форма остатка (иногда называемая Шлемильхом - Роше ). Выбор является формой Лагранжа, а выбор является формой Коши.
Эти уточнения теоремы Тейлора обычно доказываются с использованием теоремы о среднем значении , откуда и название. Кроме того, обратите внимание, что это именно теорема о среднем значении, когда . Можно встретить и другие подобные выражения. Например, если G ( t ) непрерывна на замкнутом интервале и дифференцируема с ненулевой производной на открытом интервале между и , затем
на какое-то число между и . Эта версия охватывает формы остатка Лагранжа и Коши как частные случаи и доказывается ниже с использованием теоремы Коши о среднем значении . Форма Лагранжа получается, если взять а форма Коши получается, если взять .
Утверждение об интегральной форме остатка является более сложным, чем предыдущие, и требует понимания теории интегрирования Лебега для полной общности. Однако это справедливо и в смысле интеграла Римана при условии, что ( k + 1)-я производная от f непрерывна на замкнутом интервале [ a , x ].
Целая форма остатка [10] - Позволять быть абсолютно непрерывным на замкнутом интервале между и . Затем
Ввиду непрерывности f абсолютной ( к ) на замкнутом интервале между и , его производная f ( к +1) существует как L 1 -функция, и результат может быть доказан формальным вычислением с использованием фундаментальной теоремы исчисления и интегрирования по частям .
Оценки на остаток
[ редактировать ]На практике часто бывает полезно иметь возможность оценить остаточный член, появляющийся в приближении Тейлора, вместо того, чтобы иметь для него точную формулу. Предположим, что ( f k + 1) -раз непрерывно дифференцируема в интервале I, содержащем a . Предположим, что существуют вещественные константы q и Q такие, что
протяжении Я. на Тогда остаточный член удовлетворяет неравенству [11]
если x > a , и аналогичная оценка, если x < a . Это простое следствие лагранжевой формы остатка. В частности, если
на интервале I = ( a − r , a + r ) с некоторым , затем
для всех x ∈ ( а - р , а + р ). Второе неравенство называется равномерной оценкой , поскольку оно выполняется равномерно для всех x на интервале ( a − r , a + r ).
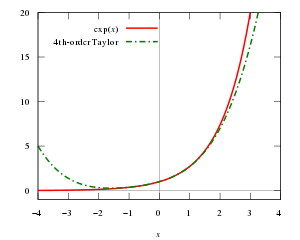
Пример
[ редактировать ]
Предположим, что мы хотим найти приближенное значение функции на интервале при этом обеспечивая погрешность аппроксимации не более 10 −5 . В этом примере мы притворяемся, что знаем только следующие свойства показательной функции:
| ( ★ ) |
Из этих свойств следует, что для всех и, в частности, . Следовательно Полином Тейлора -го порядка в и его остаточный член в форме Лагранжа равны
где какое-то число между 0 и x . Поскольку е х увеличивается на ( ★ ), мы можем просто использовать для оценить остаток на подинтервале . Чтобы получить верхнюю оценку остатка от , мы используем свойство для оценить
используя разложение Тейлора второго порядка. Затем мы решаем для e х сделать вывод, что
просто максимизируя числитель и минимизируя знаменатель . Объединив эти оценки для e х мы видим это
поэтому требуемая точность заведомо достигается, когда
(См. факториал или вычислите вручную значения и .) В заключение теорема Тейлора приводит к приближению
Например, это приближение дает десятичное выражение , исправьте до пяти десятичных знаков.
Связь с аналитичностью
[ редактировать ]Разложения Тейлора действительных аналитических функций
[ редактировать ]Пусть I ⊂ R — открытый интервал . По определению функция f : I → R является вещественно-аналитической , если она локально определяется сходящимся степенным рядом . что для каждого a ∈ I существует некоторое r > 0 и последовательность коэффициентов ck R ∈ Это означает , такие, что ( a − r , a + r ) ⊂ I и
В общем случае радиус сходимости степенного ряда можно вычислить по формуле Коши – Адамара.
Этот результат основан на сравнении с геометрическим рядом , и тот же метод показывает, что если степенной ряд, основанный на a, сходится для некоторого b ∈ R , он должен сходиться равномерно на замкнутом интервале , где . Здесь рассматривается только сходимость степенного ряда, и вполне может быть, что ( a − R , a + R ) выходит за пределы области определения I функции f .
Полиномы Тейлора действительной аналитической функции f в точке a представляют собой просто конечные отсечения
его локально определяющего степенного ряда, а соответствующие остаточные члены локально задаются аналитическими функциями
Здесь функции
также являются аналитическими, поскольку их определяющие степенные ряды имеют тот же радиус сходимости, что и исходный ряд. Предполагая, что [ a − r , a + r ] ⊂ I и r < R , все эти ряды сходятся равномерно на ( a − r , a + r ) . Естественно, в случае аналитических функций можно оценить остаточный член хвостом последовательности производных f′ ( a ) в центре разложения, но при использовании комплексного анализа возникает и другая возможность, которая описана ниже .
Теорема Тейлора и сходимость рядов Тейлора
[ редактировать ]Ряд Тейлора для f сходится в некотором интервале, в котором все его производные ограничены и не растут слишком быстро при стремлении k к бесконечности. (Однако, даже если ряд Тейлора сходится, он может не сходиться к f , как объясняется ниже; в этом случае f называется неаналитическим . )
Можно подумать о сериале Тейлора
бесконечно много раз дифференцируемой функции f : R → R как ее «полином Тейлора бесконечного порядка» в точке a . Теперь оценки остатка подразумевают, что если для любого r производные f известны как ограниченные над ( a − r , a + r ), то для любого порядка k и для любого r > 0 существует константа M k,r > 0 такое, что
| ( ★★ ) |
для каждого x ∈ ( а - р , а + р ). Иногда константы M k,r можно выбрать таким образом, чтобы M k,r было ограничено сверху для фиксированного r и всех k . Тогда ряд Тейлора функции f сходится равномерно к некоторой аналитической функции
(Сходимость также достигается, даже если M k,r не ограничена сверху, если оно растет достаточно медленно.)
Предельная функция T f по определению всегда аналитична, но она не обязательно равна исходной функции f , даже если f бесконечно дифференцируема. В этом случае мы говорим, что f — неаналитическая гладкая функция , например плоская функция :
используя цепное правило Повторно методом математической индукции , можно показать, что для любого k порядка
для некоторого многочлена p k степени 2( k − 1). Функция стремится к нулю быстрее, чем любой полином, поскольку , поэтому f бесконечно много раз дифференцируема и f ( к ) (0) = 0 для любого натурального числа k . Все приведенные выше результаты справедливы и в этом случае:
- Ряд Тейлора функции f сходится равномерно к нулевой функции T f ( x ) = 0, которая является аналитической со всеми коэффициентами, равными нулю.
- Функция f не равна этому ряду Тейлора и, следовательно, неаналитическая.
- Для любого порядка k ∈ N и радиуса r > 0 существует M k,r > 0, удовлетворяющий указанной выше границе остатка ( ★★ ).
Однако по мере увеличения k при фиксированном r значение M k,r растет быстрее, чем r к , и ошибка не стремится к нулю .
Теорема Тейлора в комплексном анализе
[ редактировать ]Теорема Тейлора обобщается на функции f : C → C , которые комплексно дифференцируемы в открытом подмножестве U ⊂ C комплексной плоскости . Однако его полезность затмевается другими общими теоремами комплексного анализа . А именно, более сильные версии связанных результатов можно вывести для комплексных дифференцируемых функций f : U → C, используя интегральную формулу Коши следующим образом.
Пусть r > 0 такое, что замкнутый диск B ( z , r ) ∪ S ( z , r содержится в U. ) Тогда интегральная формула Коши с положительной параметризацией γ ( t ) = z + re это круга S ( z , r ) с дает
Здесь все подынтегральные выражения непрерывны на окружности S ( z , r ), что и оправдывает дифференцирование под знаком интеграла. В частности, если f однажды комплексно дифференцируема на открытом множестве U деле она бесконечно много раз комплексно дифференцируема на U. , то на самом Также получены оценки Коши [12]
для любого z ∈ U и r > 0 такого, что B ( z , r ) ∪ S ( c , r ) ⊂ U . Из этих оценок следует, что комплексный ряд Тейлора
функции f сходится равномерно на любом открытом диске с в некоторую функцию T f . Кроме того, используя формулы контурного интеграла для производных f ( к ) ( с ),
поэтому любая комплексная дифференцируемая функция f в открытом множестве U ⊂ C на самом деле является комплексно-аналитической . Все сказанное здесь для вещественных аналитических функций справедливо и для комплексных аналитических функций с заменой открытого интервала I на открытое подмножество U ∈ C и a -центрированных интервалов ( a − r , a + r ) заменой c -центрированных дисков B ( в , р ). В частности, разложение Тейлора имеет вид
где остаточный член R k комплексно-аналитический. Методы комплексного анализа дают некоторые мощные результаты в отношении расширений Тейлора. Например, используя интегральную формулу Коши для любой положительно ориентированной жордановой кривой который параметризует границу региона , получаем выражения для производных f ( Дж ) ( c ), как указано выше, и немного изменив вычисление для T f ( z ) = f ( z ) , можно прийти к точной формуле
Важной особенностью здесь является то, что качество аппроксимации полиномом Тейлора в области доминируют значения самой функции f на границе . Аналогично, применяя оценки Коши к выражению ряда для остатка, получаем равномерные оценки
Пример
[ редактировать ]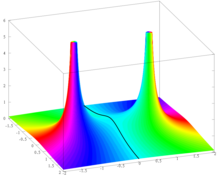
Функция
является вещественно аналитическим , то есть локально определяется своим рядом Тейлора. Эта функция была построена выше, чтобы проиллюстрировать тот факт, что некоторые элементарные функции не могут быть аппроксимированы полиномами Тейлора в слишком больших окрестностях центра разложения. Такое поведение легко понять в рамках комплексного анализа. А именно, функция f продолжается в мероморфную функцию
на компактифицированной комплексной плоскости. Он имеет простые полюса на и , и в другом месте оно аналитично. Теперь его ряд Тейлора с центром в точке на сходится любом круге B ( z0 z0 , r ) с r < | z − z 0 |, где тот же ряд Тейлора сходится в точке z ∈ C . Следовательно, ряд Тейлора для f с центром в точке 0 сходится на B (0, 1) и не сходится ни при каком z ∈ C , где | г | > 1 из-за полюсов в точках i и − i . По той же причине ряд Тейлора функции f с центром в точке 1 сходится на и не сходится ни при каком z ∈ C, таком, что .
Обобщения теоремы Тейлора
[ редактировать ]Дифференцируемость высшего порядка
[ редактировать ]Функция f : R н → R дифференцируемо ∈ в a R точке н тогда и только тогда, когда существует линейный функционал L : R н → R и функция h : R н → R такой, что
Если это так, то является (единственно определенным) f в дифференциалом точке a . Более того, тогда частные производные f , а существуют в точке a дифференциал f в точке a определяется выражением
Введение мультииндексной нотации
для α ∈ N н и x ∈ R н . Если все -го порядка Частные производные от f : R н → R непрерывны в точке a ∈ R н , то по теореме Клеро можно изменить порядок смешанных производных при a , поэтому обозначение
более высокого порядка для частных производных в этой ситуации оправдано. То же самое верно, если все частные производные ( k − 1 )-го порядка от f существуют в некоторой окрестности a и дифференцируемы в точке a . [13] Тогда мы говорим, что f k раз дифференцируема в точке a .
Теорема Тейлора для функций многих переменных
[ редактировать ]Используя обозначения предыдущего раздела, получаем следующую теорему.
Многомерная версия теоремы Тейлора [14] — Пусть f : R н → R — k -кратно непрерывно дифференцируемая функция в точке a ∈ R н . Тогда существуют функции h α : R н → R , где такой, что
Если функция f : R н → R k замкнутом + 1 раз непрерывно дифференцируем в шаре для некоторых , то можно вывести точную формулу остатка через ( k +1 )-го порядка частные производные от f в этой окрестности. [15] А именно,
В этом случае в силу непрерывности ( k +1 )-го порядка частных производных в компакте B сразу получаются равномерные оценки
Пример в двух измерениях
[ редактировать ]Например, полином Тейлора третьего порядка гладкой функции есть, обозначающий ,
Доказательства
[ редактировать ]Доказательство теоремы Тейлора для одной действительной переменной.
[ редактировать ]Позволять [16]
где, как и в формулировке теоремы Тейлора,
Достаточно показать, что
Доказательство здесь основано на неоднократном применении правила Лопиталя . Обратите внимание, что для каждого , . Следовательно, каждый из первых производные числителя в исчезает в , и то же самое относится и к знаменателю. Кроме того, поскольку условие, что функция быть раз дифференцируема в точке, требует дифференцируемости до порядка в окрестности указанной точки (это верно, поскольку дифференцируемость требует, чтобы функция была определена во всей окрестности точки), числитель и его производные дифференцируемы в окрестности . Ясно, что знаменатель также удовлетворяет указанному условию и, кроме того, не обращается в нуль, если , следовательно, все условия, необходимые для правила Лопиталя, выполнены и его применение оправдано. Так
где предпоследнее равенство следует из определения производной при .
Альтернативное доказательство теоремы Тейлора для одной действительной переменной
[ редактировать ]Позволять — любая непрерывная функция с действительным знаком, которую можно аппроксимировать полиномом Тейлора.
Шаг 1: Пусть и быть функциями. Набор и быть
Шаг 2: Свойства и :
Сходным образом,
Шаг 3. Используйте теорему Коши о среднем значении
Позволять и быть непрерывными функциями на . С поэтому мы можем работать с интервалом . Позволять и быть дифференцируемым на . Предполагать для всех .Тогда существует такой, что
Примечание: в и так
для некоторых .
Это также может быть выполнено для :
для некоторых .Это можно продолжать и дальше .
Это дает раздел в :
с
Набор :
Шаг 4: Замените обратно
По правилу власти повторяющиеся производные , , так:
Это приводит к:
Переставив, получим:
или потому что в конце концов:
Вывод средних форм остатка
[ редактировать ]Пусть G — любая вещественная функция, непрерывная на отрезке между и и дифференцируема с ненулевой производной на открытом интервале между и и определить
Для . Тогда по Коши о среднем значении теореме
| ( ★★★ ) |
для некоторых на открытом промежутке между и . Обратите внимание, что здесь числитель является в точности остатком полинома Тейлора для . Вычислить
подключите его к ( ★★★ ) и переставьте члены, чтобы найти это
Это форма остаточного члена, упомянутая после фактической формулировки теоремы Тейлора с остатком в форме среднего значения.Лагранжевую форму остатка можно найти выбором и форму Коши, выбрав .
Замечание. Используя этот метод, можно также восстановить целую форму остатка, выбрав
но требования к f, необходимые для использования теоремы о среднем значении, слишком строги, если кто-то стремится доказать утверждение в случае, когда f ( к ) только абсолютно непрерывен . использовать интеграл Римана Однако если вместо интеграла Лебега , предположения нельзя ослабить.
Вывод интегральной формы остатка
[ редактировать ]Благодаря абсолютной преемственности на замкнутом интервале между и его производная существует как -функция, и мы можем использовать фундаментальную теорему исчисления и интегрирования по частям . То же самое доказательство применимо и для интеграла Римана, предполагая, что непрерывна дифференцируема замкнутом интервале и на на открытом интервале между и , и это приводит к тому же результату, что и использование теоремы о среднем значении.
Основная теорема исчисления гласит, что
Теперь мы можем интегрировать по частям и снова использовать фундаментальную теорему исчисления, чтобы увидеть, что
что в точности является теоремой Тейлора с остатком в интегральной форме в случае . Общее утверждение доказывается с помощью индукции . Предположим, что
| ( уравнение 1 ) |
Интегрируя остаточный член по частям, приходим к
Подстановка этого в формулу ( eq1 ) показывает, что если это справедливо для значения , оно также должно выполняться для значения . Следовательно, поскольку оно справедливо для , оно должно выполняться для каждого положительного целого числа .
Вывод остатка многомерных полиномов Тейлора
[ редактировать ]Докажем частный случай, когда имеет непрерывные частные производные до порядка в каком-то закрытом шаре с центром . Стратегия доказательства состоит в том, чтобы применить случай теоремы Тейлора с одной переменной к ограничению к отрезку, примыкающему к и . [17] Параметризируйте отрезок между и к Применим версию теоремы Тейлора для одной переменной к функции :
Применение правила цепочки для нескольких переменных дает
где – полиномиальный коэффициент . С , мы получаем:
См. также
[ редактировать ]- Лемма Адамара
- Ряд Лорана – Степенной ряд с отрицательными степенями.
- Аппроксимант Паде - «лучшее» приближение функции рациональной функцией заданного порядка.
- Серия Newton – дискретный аналог производных
- Теория приближений - Теория получения приемлемо близких неточных математических расчетов.
- Аппроксимация функции - аппроксимация произвольной функции хорошо работающей.
Сноски
[ редактировать ]- ^ (2013). «Линейная и квадратичная аппроксимация». Дата обращения 6 декабря 2018 г.
- ^ Тейлор, Брук (1715). Methodus Incrementorum Directa et Inversa [ Прямой и обратный методы приращения ] (на латыни). Лондон. п. 21–23 (т. VII, Фем. 3, Кор. 2). Переведено на английский язык в Струйк, диджей (1969). Справочник по математике 1200–1800 гг . Кембридж, Массачусетс: Издательство Гарвардского университета. стр. 329–332.
- ^ Клайн 1972 , стр. 442, 464.
- ^ Дженокки, Анджело; Пеано, Джузеппе (1884), Дифференциальное исчисление и принципы интегрального исчисления , (N. 67, стр. XVII – XIX): Fratelli Bocca ed.
{{citation}}: CS1 maint: местоположение ( ссылка ) - ^ Спивак, Майкл (1994), Исчисление (3-е изд.), Хьюстон, Техас: Опубликуй или погибни, стр. 383, ISBN 978-0-914098-89-8
- ^ «Формула Тейлора» , Математическая энциклопедия , EMS Press , 2001 [1994]
- ^ Гипотеза f ( к ) непрерывен на замкнутом интервале между и является не лишним. Хотя f в k + 1 раз дифференцируема на открытом интервале между и подразумевает, что f ( к ) непрерывна на открытом интервале между и , это не означает, что f ( к ) непрерывен на замкнутом интервале между и , т.е. это не означает, что f ( к ) непрерывна концах на . этого интервала Рассмотрим, например, функцию f : [0,1] → R, определенную как равную на и с . Это не непрерывно в 0 , но непрерывно в . Более того, можно показать, что эта функция имеет первообразную . эта первообразная дифференцируема Следовательно , по , ее производная функция f ) непрерывна на отрезке ( ее производная f является не непрерывной на отрезке , но . Таким образом, в данном случае теорема неприменима.
- ^ Кляйн 1998 , §20.3; Апостол 1967 , §7.7.
- ^ Апостол 1967 , §7.7.
- ^ Апостол 1967 , §7.5.
- ^ Апостол 1967 , §7.6
- ^ Рудин 1987 , §10.26
- ^ Это следует из многократного применения теоремы о том, что если частные производные функции f существуют в окрестности a и непрерывны в точке a , то функция дифференцируема в точке a . См., например, Апостол 1974 , теорема 12.11.
- ^ Кенигсбергский анализ 2, с. 64 и далее.
- ^ Фолланд, ГБ «Производные высшего порядка и формула Тейлора с несколькими переменными» (PDF) . Кафедра математики | Университет Вашингтона . Проверено 21 февраля 2024 г.
- ^ Стромберг 1981
- ^ Хёрмандер 1976 , стр. 12–13.
Ссылки
[ редактировать ]- Апостол, Том (1967), Исчисление , Уайли, ISBN 0-471-00005-1 .
- Апостол, Том (1974), Математический анализ , Аддисон – Уэсли .
- Бартл, Роберт Г.; Шерберт, Дональд Р. (2011), Введение в реальный анализ (4-е изд.), Wiley, ISBN 978-0-471-43331-6 .
- Хёрмандер, Л. (1976), Линейные операторы с частными производными, Том 1 , Springer, ISBN 978-3-540-00662-6 .
- Клайн, Моррис (1972), Математическая мысль от древних до наших дней, Том 2 , Oxford University Press .
- Клайн, Моррис (1998), Исчисление: интуитивный и физический подход , Дувр, ISBN 0-486-40453-6 .
- Педрик, Джордж (1994), Первый курс анализа , Springer, ISBN 0-387-94108-8 .
- Стромберг, Карл (1981), Введение в классический реальный анализ , Уодсворт, ISBN 978-0-534-98012-2 .
- Рудин, Уолтер (1987), Реальный и комплексный анализ (3-е изд.), McGraw-Hill, ISBN 0-07-054234-1 .
- Тао, Теренс (2014), Анализ, Том I (3-е изд.), Книжное агентство Hindustan, ISBN 978-93-80250-64-9 .
- Доказательство теоремы Тейлора (PDF) , Китайский университет Гонконга .
Внешние ссылки
[ редактировать ]- Теорема Тейлора в ProofWiki
- Приближение косинуса рядами Тейлора при разрезании узла
- Trigonometric Taylor Expansion Интерактивный демонстрационный апплет
- Возвращение к серии Тейлора в Институте целостных численных методов
































































![{\textstyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70a2d2aa48bad27a96e8cad0fb1efd22f102b787)







![{\textstyle x\in [-1,0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c679bb820c0ff16e506ccbaf2fa3ca3a1c48835a)
![{\displaystyle [-1,0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a19442d946499667f5bd3ddf8478ca48a0ec38a)
![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)












![{\textstyle [a-r_{b},a+r_{b}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8f4fd7273a553214dae5eed8b71d1c24ad65a09)



![{\displaystyle {\begin{aligned}&h_{k}:(ar,a+r)\to \mathbb {R} \\[1ex]&h_{k}(x)=(xa)\sum _{j= 0}^{\infty }c_{k+1+j}\left(xa\right)^{j}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06bc79a4930ba957e7865e79d857e1713a921f97)








![{\displaystyle т\in [0,2\pi]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8dbc9ed8510c75442ce1d2e73f021258fc7e04c6)













































![{\displaystyle {\begin{aligned}\lim _{x\to a}{\frac {f(x)-P(x)}{(xa)^{k}}} &=\lim _{x\ to a}{\frac {{\frac {d}{dx}}(f(x)-P(x))}{{\frac {d}{dx}}(xa)^{k}}}\ \[1ex]&=\cdots \\[1ex]&=\lim _{x\to a}{\frac {{\frac {d^{k-1}}{dx^{k-1}}} (f(x)-P(x))}{{\frac {d^{k-1}}{dx^{k-1}}}(xa)^{k}}}\\[1ex]& = {\frac {1}{k!}}\lim _{x\to a}{\frac {f^{(k-1)}(x)-P^{(k-1)}(x) }{xa}}\\[1ex]&={\frac {1}{k!}}(f^{(k)}(a)-P^{(k)}(a))=0\end {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/702530141443e9d6fda222067ccfe3fbdf78db8e)










![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)

![{\displaystyle [а,х]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/692f0edd0d40232c8a69ed5de7b142e1e343eff7)


























![{\displaystyle т\in [a,x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/357000ec9c6100c2feacc3ca061fa2b3c854be00)












![{\displaystyle {\begin{aligned}\int _{a}^{x}{\frac {f^{(k+1)}(t)}{k!}}(xt)^{k}\, dt=&-\left[{\frac {f^{(k+1)}(t)}{(k+1)k!}}(xt)^{k+1}\right]_{a} ^{x}+\int _{a}^{x}{\frac {f^{(k+2)}(t)}{(k+1)k!}}(xt)^{k+1 }\,dt\\=&\ {\frac {f^{(k+1)}(a)}{(k+1)!}}(xa)^{k+1}+\int _{a }^{x}{\frac {f^{(k+2)}(t)}{(k+1)!}}(xt)^{k+1}\,dt.\end{aligned}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6389635717cc93be2b76539da45a18411376e16)















![{\displaystyle (0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e70f9c241f9faa8e9fdda2e8b238e288807d7a4)

