Сетка (многогранник)


В геометрии сеть гранями многогранника , — это совокупность непересекающихся ребрами соединенных многоугольников, на плоскости , которые можно сложить (вдоль ребер), чтобы стать многогранника . Многогранные сети являются полезным подспорьем при изучении многогранников и объемной геометрии в целом, поскольку они позволяют строить физические модели многогранников из такого материала, как тонкий картон. [1]
Ранний пример многогранных сетей появляется в работах Альбрехта Дюрера , чья книга 1525 года «Курс искусства измерения с помощью циркуля и линейки» ( Unterweysung der Messung mit dem Zyrkel und Rychtscheyd ) включала сети для платоновых тел и некоторых архимедовых тел. . [2] [3] Эти конструкции впервые назвал сетями в 1543 году Августин Хиршфогель . [4]
Существование и уникальность
[ редактировать ]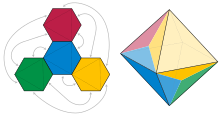
Для данного многогранника может существовать множество различных сетей, в зависимости от выбора того, какие ребра соединены, а какие разделены. Ребра, которые вырезаны из выпуклого многогранника для формирования сети, должны образовывать остовное дерево многогранника, но вырезание некоторых остовных деревьев может привести к самоперекрытию многогранника при развертывании, а не к формированию сети. [5] И наоборот, данная сеть может складываться в несколько различных выпуклых многогранников, в зависимости от углов, под которыми сложены ее края, и выбора того, какие ребра склеить. [6] Если дана сетка с образцом склейки ее ребер, такая, что каждая вершина полученной фигуры имеет положительный угловой дефект и сумма этих дефектов равна ровно 4 π , то обязательно существует ровно один многогранник, который можно сложенный из него; это теорема единственности Александрова . Однако сформированный таким образом многогранник может иметь грани, отличные от тех, которые указаны как часть сети: некоторые из сетевых многоугольников могут иметь складки поперек них, а некоторые ребра между чистыми многоугольниками могут оставаться развернутыми. Кроме того, одна и та же сеть может иметь несколько допустимых шаблонов склейки, что приводит к образованию разных сложенных многогранников. [7]
В 1975 году Шепард задался вопросом, имеет ли каждый выпуклый многогранник хотя бы одну сеть или простое развертывание ребер. [8] Этот вопрос, который также известен как гипотеза Дюрера или проблема развертывания Дюрера, остается без ответа. [9] [10] [11] Существуют невыпуклые многогранники, не имеющие сетей, и можно разделить грани каждого выпуклого многогранника (например, по разрезу ) так, чтобы множество разделенных граней имело сеть. [5] В 2014 году Мохаммад Гоми допускает сеть показал, что каждый выпуклый многогранник после аффинного преобразования . [12] Кроме того, в 2019 году Барвинок и Гоми показали, что обобщение гипотезы Дюрера неверно для псевдоребер : [13] т. е. сеть геодезических, соединяющих вершины многогранника и образующих граф с выпуклыми гранями.

Связанный с этим открытый вопрос заключается в том, имеет ли каждая сеть выпуклого многогранника « блуминг » — непрерывное несамопересекающееся движение из плоского состояния в сложенное, которое сохраняет каждую грань плоской на протяжении всего движения. [14]
Кратчайший путь
[ редактировать ]Кратчайший путь по поверхности между двумя точками на поверхности многогранника соответствует прямой линии на подходящей сети для подмножества граней, которых касается путь. Сеть должна быть такой, чтобы прямая линия полностью находилась внутри нее, и, возможно, придется рассмотреть несколько сетей, чтобы увидеть, какая из них дает кратчайший путь. Например, в случае куба , если точки находятся на соседних гранях, одним кандидатом на кратчайший путь является путь, пересекающий общее ребро; кратчайший путь такого типа находится с помощью сети, в которой две грани также смежны. Другие кандидаты на кратчайший путь проходят через поверхность третьей грани, примыкающей к обеим (их две), и соответствующие сети можно использовать для поиска кратчайшего пути в каждой категории. [15]
Задача о пауке и мухе — это развлекательная математическая головоломка, в которой нужно найти кратчайший путь между двумя точками кубоида.
Многогранные сети более высокой размерности
[ редактировать ]
Сеть 4-многогранника , четырехмерного многогранника , состоит из многогранных ячеек , соединенных своими гранями и занимающих все одно и то же трехмерное пространство, подобно тому, как многогранные грани сети многогранника соединены своими края и все занимают одну и ту же плоскость. Сеть тессеракта, четырехмерного гиперкуба , широко используется в картине Сальвадора Дали « Распятие (Corpus Hypercubus)» (1954). [16] Та же самая сеть тессеракта занимает центральное место в сюжете рассказа «И он построил кривой дом» Роберта Хайнлайна . [17]
Число комбинаторно различных сетей -мерные гиперкубы можно найти, представляя эти сети в виде дерева на узлы, описывающие шаблон, по которому пары граней гиперкуба склеиваются вместе, образуя сеть, вместе с идеальным сопоставлением на графе дополнений дерева, описывающего пары граней, противоположных друг другу в свернутом гиперкубе. Используя это представление, количество различных разверток гиперкубов размерностей 2, 3, 4,... было подсчитано как
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Веннингер, Магнус Дж. (1971), Модели многогранников , Издательство Кембриджского университета
- ^ Дюрер, Альбрехт (1525), Инструкция по измерению с помощью Zyrkel и Rychtscheyd , Нюрнберг: Мюнхен, Süddeutsche Monatheft, стр. 139–152 . Английский перевод с комментариями на Штраус, Уолтер Л. (1977), Руководство художника , Нью-Йорк
{{citation}}: CS1 maint: отсутствует местоположение издателя ( ссылка ) - ↑ Шрайбер, Фишер и Штернат утверждают, что раньше Дюрера Леонардо да Винчи нарисовал несколько сетей для Пачоли » Луки «Божественной пропорции , включая сеть для правильного додекаэдра. Однако их нельзя найти ни в онлайн-копиях первого печатного издания этой работы 1509 года , ни в Женевской рукописи 1498 года 210 , поэтому это утверждение следует считать непроверенным. Видеть: Шрайбер, Питер; Фишер, Гизела ; Стернат, Мария Луиза (июль 2008 г.), «Новый взгляд на повторное открытие архимедовых тел в эпоху Возрождения», Архив истории точных наук , 62 (4): 457–467, JSTOR 41134285
- ^ Фридман, Майкл (2018), История складывания в математике: математизация полей , Science Networks. Исторические исследования, том. 59, Биркхойзер, с. 8, номер домена : 10.1007/978-3-319-72487-4 , ISBN 978-3-319-72486-7
- ^ Jump up to: Перейти обратно: а б Демейн, Эрик Д .; О'Рурк, Джозеф (2007), «Глава 22. Развертывание ребер многогранников», Геометрические алгоритмы складывания: связи, оригами, многогранники , Cambridge University Press, стр. 306–338
- ^ Малкевич, Джозеф, «Сети: инструмент для представления многогранников в двух измерениях» , тематические колонки , Американское математическое общество , получено 14 мая 2014 г.
- ^ Демейн, Эрик Д .; Демейн, Мартин Л .; Любив, Анна ; О'Рурк, Джозеф (2002), «Перечисление свертываний и разверток между многоугольниками и многогранниками», Graphs and Combinatorics , 18 (1): 93–104, arXiv : cs.CG/0107024 , doi : 10.1007/s003730200005 , MR 1892436 , S2CID 1489
- ^ Шепард, GC (1975), «Выпуклые многогранники с выпуклыми сетями», Mathematical Proceedings of the Cambridge Philosophical Society , 78 (3): 389–403, Bibcode : 1975MPCPS..78..389S , doi : 10.1017/s0305004100051860 , MR 0390 915 , S2CID 122287769
- ^ Вайсштейн, Эрик В. , «Гипотеза Шепарда» , MathWorld
- ^ Москович, Д. (4 июня 2012 г.), «Гипотеза Дюрера» , Открытый сад проблем.
- ^ Гоми, Мохаммад (01 января 2018 г.), «Проблема развертывания Дюрера для выпуклых многогранников», Уведомления Американского математического общества , 65 (1): 25–27, doi : 10.1090/noti1609
- ^ Гоми, Мохаммад (2014), «Аффинные развертки выпуклых многогранников», Geom. Тополь. , 18 (5): 3055–3090, arXiv : 1305.3231 , Bibcode : 2013arXiv1305.3231G , doi : 10.2140/gt.2014.18.3055 , S2CID 16827957
- ^ Барвинок, Николай; Гоми, Мохаммад (03 апреля 2019 г.), «Псевдокраевые развертки выпуклых многогранников», Дискретная и вычислительная геометрия , 64 (3): 671–689, arXiv : 1709.04944 , doi : 10.1007/s00454-019-00082-1 , ISSN 0179-5376 , S2CID 37547025
- ^ Миллер, Эзра; Пак, Игорь (2008), «Метрическая комбинаторика выпуклых многогранников: разрезные локусы и неперекрывающиеся развертки», Discrete & Computational Geometry , 39 (1–3): 339–388, doi : 10.1007/s00454-008-9052-3 , MR 2383765
- ^ О'Рурк, Джозеф (2011), Как сложить: математика связей, оригами и многогранников , Cambridge University Press, стр. 115–116, ISBN 9781139498548
- ^ Кемп, Мартин (1 января 1998 г.), «Измерения Дали», Nature , 391 (6662): 27, Бибкод : 1998Natur.391...27K , doi : 10.1038/34063 , S2CID 5317132
- ^ Хендерсон, Линда Дэлримпл (ноябрь 2014 г.), «Научная фантастика, искусство и четвертое измерение», в Эммер, Мишель (редактор), Imagine Math 3: Между культурой и математикой , Springer International Publishing, стр. 69–84, doi : 10.1007/978-3-319-01231-5_7

