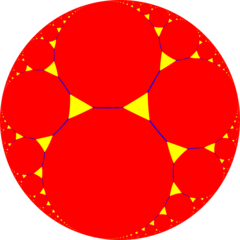
Шестиугольная сотовая плитка
| Шестиугольная сотовая плитка | |
|---|---|
 Перспективная проекция в рамках модели диска Пуанкаре | |
| Тип | Гиперболические обычные соты Паракомпактный однородный сотовый |
| Символы Шлефли | {6,3,3} т{3,6,3} 2т{6,3,6} 2т{6,3 [3] } т{3 [3,3] } |
| Диаграммы Кокстера | |
| Клетки | {6,3} |
| Лица | шестигранник {6} |
| Краевая фигура | треугольник {3} |
| Вершинная фигура |  тетраэдр {3,3} |
| Двойной | Тетраэдрические соты порядка 6 |
| Группы Кокстера | , [3,3,6] , [3,6,3] , [6,3,6] , [6,3 [3] ] , [3 [3,3] ] |
| Характеристики | Обычный |
В области гиперболической геометрии шестиугольная мозаика является одной из 11 правильных паракомпактных сот в трехмерном гиперболическом пространстве . Он паракомпактен , поскольку имеет ячейки , состоящие из бесконечного числа граней. Каждая ячейка представляет собой шестиугольную мозаику , вершины которой лежат на орисфере — поверхности в гиперболическом пространстве, приближающейся к единственной идеальной точке на бесконечности.
Символ Шлефли шестиугольных сот — {6,3,3}. Поскольку значение шестиугольной мозаики равно {6,3}, в этой соте есть три таких шестиугольных мозаики, сходящихся на каждом ребре. Поскольку символом Шлефли тетраэдра является {3,3}, вершинной фигурой этой соты является тетраэдр. Таким образом, в каждой вершине этой соты встречаются четыре шестиугольных мозаики, в каждой вершине встречаются шесть шестиугольников и в каждой вершине встречаются четыре ребра. [1]
Изображения
[ редактировать ]Если смотреть в перспективе за пределами модели диска Пуанкаре , изображение выше показывает одну шестиугольную ячейку мозаики внутри сот и ее орисферу среднего радиуса (оросфера, падающая с краевыми средними точками). В этой проекции шестиугольники становятся бесконечно малыми по направлению к бесконечной границе, асимптотически приближаясь к одной идеальной точке. Его можно рассматривать как похожее на апейрогональное замощение порядка 3 , {∞,3} из H 2 , с орициклами, описывающими вершины апейрогонов .
| {6,3,3} | {∞,3} |
|---|---|
 | 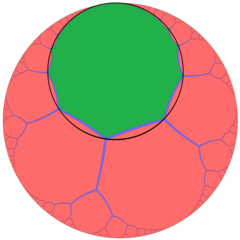 |
| Одна шестиугольная ячейка сотовой мозаики | Апейрогон 3-го порядка с зеленым апейрогоном и его орициклом. |
Симметричные конструкции
[ редактировать ]
Всего он состоит из пяти отражательных конструкций из пяти связанных групп Кокстера, все с четырьмя зеркалами, и только первое из них является правильным: ![]()
![]()
![]()
![]()
![]()
![]()
![]() [6,3,3],
[6,3,3], ![]()
![]()
![]()
![]()
![]()
![]()
![]() [3,6,3],
[3,6,3], ![]()
![]()
![]()
![]()
![]()
![]()
![]() [6,3,6],
[6,3,6], ![]()
![]()
![]()
![]()
![]() [6,3 [3] ] и [3 [3,3] ]
[6,3 [3] ] и [3 [3,3] ] ![]()
![]()
![]() , имеющие в 1, 4, 6, 12 и 24 раза большие фундаментальные домены соответственно . В разметках подгрупп нотации Коксетера они связаны следующим образом: [6,(3,3) * ] (удалить 3 зеркала, индекс 24 подгруппы); [3,6,3 * ] или [3 * ,6,3] (удалить 2 зеркала, индекс 6 подгруппы); [1 + ,6,3,6,1 + ] (удалить два ортогональных зеркала, подгруппа индекса 4); все они изоморфны [3 [3,3] ]. Кольцевые диаграммы Кокстера:
, имеющие в 1, 4, 6, 12 и 24 раза большие фундаментальные домены соответственно . В разметках подгрупп нотации Коксетера они связаны следующим образом: [6,(3,3) * ] (удалить 3 зеркала, индекс 24 подгруппы); [3,6,3 * ] или [3 * ,6,3] (удалить 2 зеркала, индекс 6 подгруппы); [1 + ,6,3,6,1 + ] (удалить два ортогональных зеркала, подгруппа индекса 4); все они изоморфны [3 [3,3] ]. Кольцевые диаграммы Кокстера: ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]() и
и ![]()
![]()
![]() , представляющие разные типы (цвета) шестиугольных мозаик в конструкции Витгофа .
, представляющие разные типы (цвета) шестиугольных мозаик в конструкции Витгофа .
Связанные многогранники и соты
[ редактировать ]Шестиугольная мозаика представляет собой правильную гиперболическую соту в трехмерном пространстве и одну из 11 паракомпактных ячеек.
| 11 паракомпактных стандартных сот | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 {6,3,3} |  {6,3,4} |  {6,3,5} |  {6,3,6} |  {4,4,3} |  {4,4,4} | ||||||
 {3,3,6} |  {4,3,6} |  {5,3,6} |  {3,6,3} |  {3,4,4} | |||||||
Это одна из 15 однородных паракомпактных сот в группе [6,3,3] Кокстера, наряду с ее двойником, тетраэдрическими сотами 6-го порядка .
| [6,3,3] семейные соты |
|---|
Это часть последовательности правильных полихор , которые включают 5-клеточное {3,3,3}, тессеракт {4,3,3} и 120-клеточное {5,3,3} евклидова 4-мерного пространства. наряду с другими гиперболическими сотами, содержащими тетраэдрические вершинные фигуры .
| {p,3,3} соты |
|---|
Он также является частью последовательности правильных сот формы {6,3,p}, каждая из которых состоит из шестиугольных ячеек мозаики:
| {6,3,p} соты |
|---|
Выпрямленные шестиугольные соты для плитки
[ редактировать ]| Выпрямленные шестиугольные соты для плитки | |
|---|---|
| Тип | Паракомпактный однородный сотовый |
| Символы Шлефли | г{6,3,3} или т 1 {6,3,3} |
| Диаграммы Кокстера | |
| Клетки | {3,3} г{6,3} |
| Лица | треугольник {3} шестигранник {6} |
| Вершинная фигура |  треугольная призма |
| Группы Кокстера | , [3,3,6] , [3,3 [3] ] |
| Характеристики | Вершинно-транзитивный, реберно-транзитивный |
Выпрямленные шестиугольные соты мозаики , t 1 {6,3,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() имеет тетраэдрические и тригексагональные грани мозаики с треугольной фигурой вершины призмы .
имеет тетраэдрические и тригексагональные грани мозаики с треугольной фигурой вершины призмы . ![]()
![]()
![]()
![]()
![]() полусимметричная конструкция чередует два типа тетраэдров.
полусимметричная конструкция чередует два типа тетраэдров.
| Шестиугольная сотовая плитка | Выпрямленные шестиугольные соты для плитки |
|---|---|
 |  |
| Связанные Н 2 мозаика | |
| Апейрогональная мозаика порядка 3 | Триапейрогональная черепица |
 |   |
Усеченные шестиугольные соты для черепицы
[ редактировать ]| Усеченные шестиугольные соты для черепицы | |
|---|---|
| Тип | Паракомпактный однородный сотовый |
| Символ Шлефли | т{6,3,3} или т 0,1 {6,3,3} |
| Диаграмма Кокстера | |
| Клетки | {3,3} т{6,3} |
| Лица | треугольник {3} двенадцатиугольник {12} |
| Вершинная фигура |  треугольная пирамида |
| Группы Кокстера | , [3,3,6] |
| Характеристики | Вершинно-транзитивный |
Усеченная шестиугольная черепица-соты , t 0,1 {6,3,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() имеет тетраэдрические и усеченные шестиугольные грани мозаики, с треугольной пирамиды фигурой вершины .
имеет тетраэдрические и усеченные шестиугольные грани мозаики, с треугольной пирамиды фигурой вершины .
Это похоже на двумерную гиперболическую усеченную апейрогональную мозаику третьего порядка , t{∞,3} с апейрогональными и треугольными гранями:
Разрезанные шестиугольные соты для черепицы
[ редактировать ]| Разрезанные шестиугольные соты для черепицы Двуусеченные тетраэдрические соты порядка 6 | |
|---|---|
| Тип | Паракомпактный однородный сотовый |
| Символ Шлефли | 2т{6,3,3} или т 1,2 {6,3,3} |
| Диаграмма Кокстера | |
| Клетки | т{3,3} т{3,6} |
| Лица | треугольник {3} шестигранник {6} |
| Вершинная фигура | 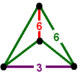 двуугольный дисфеноид |
| Группы Кокстера | , [3,3,6] , [3,3 [3] ] |
| Характеристики | Вершинно-транзитивный |
Битусеченные шестиугольные замощенные соты или битусеченные тетраэдрические соты 6-го порядка , t 1,2 {6,3,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() имеет усеченный тетраэдр и шестиугольные ячейки мозаики с дисфеноида двуугольной фигурой вершины .
имеет усеченный тетраэдр и шестиугольные ячейки мозаики с дисфеноида двуугольной фигурой вершины .
Соты из изогнутых шестиугольных плиток
[ редактировать ]| Соты из изогнутых шестиугольных плиток | |
|---|---|
| Тип | Паракомпактный однородный сотовый |
| Символ Шлефли | рр{6,3,3} или т 0,2 {6,3,3} |
| Диаграмма Кокстера | |
| Клетки | г{3,3} рр{6,3} {}×{3} |
| Лица | треугольник {3} квадрат {4} шестигранник {6} |
| Вершинная фигура | 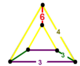 клин |
| Группы Кокстера | , [3,3,6] |
| Характеристики | Вершинно-транзитивный |
, Соты зубчатой шестиугольной черепицы t 0,2 {6,3,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() имеет октаэдр , ромбитригексагональную мозаику и треугольные призматические ячейки с клиновидной вершиной .
имеет октаэдр , ромбитригексагональную мозаику и треугольные призматические ячейки с клиновидной вершиной .
Скошенные шестиугольные соты для черепицы
[ редактировать ]| Скошенные шестиугольные соты для черепицы | |
|---|---|
| Тип | Паракомпактный однородный сотовый |
| Символ Шлефли | tr{6,3,3} или t 0,1,2 {6,3,3} |
| Диаграмма Кокстера | |
| Клетки | т{3,3} тр{6,3} {}×{3} |
| Лица | треугольник {3} квадрат {4} шестигранник {6} двенадцатиугольник {12} |
| Вершинная фигура |  зеркальная клиновидная кость |
| Группы Кокстера | , [3,3,6] |
| Характеристики | Вершинно-транзитивный |
Конусно -усеченные шестиугольные соты , t 0,1,2 {6,3,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() имеет усеченный тетраэдр , усеченную тригексагональную мозаику и треугольные призматические ячейки с зеркальной клиновидной вершиной .
имеет усеченный тетраэдр , усеченную тригексагональную мозаику и треугольные призматические ячейки с зеркальной клиновидной вершиной .
Стержневые шестиугольные соты для черепицы
[ редактировать ]| Стержневые шестиугольные соты для черепицы | |
|---|---|
| Тип | Паракомпактный однородный сотовый |
| Символ Шлефли | т 0,3 {6,3,3} |
| Диаграмма Кокстера | |
| Клетки | {3,3} {6,3} {}×{6} {}×{3} |
| Лица | треугольник {3} квадрат {4} шестигранник {6} |
| Вершинная фигура |  неправильная треугольная антипризма |
| Группы Кокстера | , [3,3,6] |
| Характеристики | Вершинно-транзитивный |
Стержень шестиугольной черепицы соты , t 0,3 {6,3,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() имеет тетраэдр , шестиугольную мозаику , шестиугольную призму и треугольные ячейки призмы с неправильной антипризмы треугольной фигурой вершины .
имеет тетраэдр , шестиугольную мозаику , шестиугольную призму и треугольные ячейки призмы с неправильной антипризмы треугольной фигурой вершины .
Соты из цитрусовых шестиугольных плиток
[ редактировать ]| Соты из цитрусовых шестиугольных плиток | |
|---|---|
| Тип | Паракомпактный однородный сотовый |
| Символ Шлефли | т 0,1,3 {6,3,3} |
| Диаграмма Кокстера | |
| Клетки | рр{3,3} {}х{3} {}х{12} т{6,3} |
| Лица | треугольник {3} квадрат {4} двенадцатиугольник {12} |
| Вершинная фигура | равнобедренно-трапециевидная пирамида |
| Группы Кокстера | , [3,3,6] |
| Характеристики | Вершинно-транзитивный |
Сусчато -усеченная шестиугольная черепица-соты , t 0,1,3 {6,3,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() имеет кубооктаэдр , треугольную призму , двенадцатиугольную призму и усеченные шестиугольные ячейки мозаики, с равнобедренно-трапециевидной пирамиды фигурой вершины .
имеет кубооктаэдр , треугольную призму , двенадцатиугольную призму и усеченные шестиугольные ячейки мозаики, с равнобедренно-трапециевидной пирамиды фигурой вершины .
Ранцикантеллярные шестиугольные соты для плитки
[ редактировать ]| Ранцикантеллярные шестиугольные соты для плитки неусеченные тетраэдрические соты порядка 6 | |
|---|---|
| Тип | Паракомпактный однородный сотовый |
| Символ Шлефли | т 0,2,3 {6,3,3} |
| Диаграмма Кокстера | |
| Клетки | т{3,3} {}x{6} рр{6,3} |
| Лица | треугольник {3} квадрат {4} шестигранник {6} |
| Вершинная фигура |  равнобедренно-трапециевидная пирамида |
| Группы Кокстера | , [3,3,6] |
| Характеристики | Вершинно-транзитивный |
Стыковые шестиугольные черепичные соты или сусечатые тетраэдрические соты 6-го порядка , t 0,2,3 {6,3,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() имеет усеченный тетраэдр , шестиугольную призму и ромбитригексагональные ячейки замощения, с равнобедренно-трапециевидной пирамиды фигурой вершины .
имеет усеченный тетраэдр , шестиугольную призму и ромбитригексагональные ячейки замощения, с равнобедренно-трапециевидной пирамиды фигурой вершины .
Всеусеченные шестиугольные соты для плитки
[ редактировать ]| Всеусеченные шестиугольные соты для плитки Всеусеченные тетраэдрические соты порядка 6 | |
|---|---|
| Тип | Паракомпактный однородный сотовый |
| Символ Шлефли | т 0,1,2,3 {6,3,3} |
| Диаграмма Кокстера | |
| Клетки | тр{3,3} {}x{6} {}х{12} тр{6,3} |
| Лица | квадрат {4} шестигранник {6} двенадцатиугольник {12} |
| Вершинная фигура | 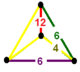 неправильный тетраэдр |
| Группы Кокстера | , [3,3,6] |
| Характеристики | Вершинно-транзитивный |
Всеусеченные шестиугольные соты или всеусеченные тетраэдрические соты 6-го порядка , t 0,1,2,3 {6,3,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() имеет усеченный октаэдр , шестиугольную призму , додекагональную призму и усеченные тригексагональные ячейки мозаики с неправильной тетраэдра фигурой вершины .
имеет усеченный октаэдр , шестиугольную призму , додекагональную призму и усеченные тригексагональные ячейки мозаики с неправильной тетраэдра фигурой вершины .
См. также
[ редактировать ]- Выпуклые однородные соты в гиперболическом пространстве
- Регулярные мозаики гиперболического трехмерного пространства
- Паракомпактные однородные соты
- Перемежающиеся шестиугольные соты для плитки
Ссылки
[ редактировать ]- ^ Коксетер Красота геометрии , 1999, Глава 10, Таблица III
- Коксетер , Правильные многогранники , 3-е. изд., Dover Publications, 1973. ISBN 0-486-61480-8 . (Таблицы I и II: Правильные многогранники и соты, стр. 294–296)
- Красота геометрии: двенадцать эссе (1999), Dover Publications, LCCN 99-35678 , ISBN 0-486-40919-8 (Глава 10, Обычные соты в гиперболическом пространстве , архивировано 10 июня 2016 г. в Wayback Machine ) Таблица III
- Джеффри Р. Уикс. Форма пространства, 2-е издание ISBN 0-8247-0709-5 (главы 16–17: Геометрии трехмерных многообразий I, II)
- Н. В. Джонсон, Р. Келлерхалс , Дж. Г. Рэтклифф, С. Т. Чанц, Размер гиперболического симплекса Кокстера , Группы преобразований (1999), Том 4, Выпуск 4, стр. 329–353 [1] [2]
- Н. В. Джонсон, Р. Келлерхалс , Дж. Г. Рэтклифф, С. Т. Чанц, Классы соизмеримости гиперболических групп Кокстера , (2002) H 3 :стр130. [3]
Внешние ссылки
[ редактировать ]- Джон Баэз , Visual Insight : {6,3,3} Honeycomb (15 марта 2014 г.)
- Джон Баэз , Visual Insight : {6,3,3} Соты в верхней половине пространства (15 сентября 2013 г.)
- Джон Баэз , Visual Insight : Усеченные соты {6,3,3} (01 декабря 2016 г.)