Целочисленный раздел

Эта статья о разбиении целого числа. Информацию о группировке элементов набора см. в разделе Разделение набора . Для исчисления разделов множеств см. Бесконечную комбинаторику .

Диаграммы Юнга соответствуют разбиениям натуральных чисел от 1 до 8. Они устроены так, что изображения при отражении относительно главной диагонали квадрата являются сопряженными разбиениями.

Разделы n с наибольшей частью k

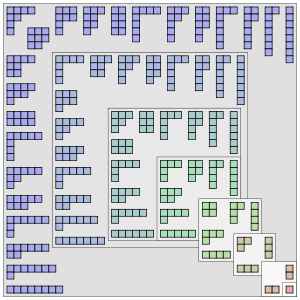
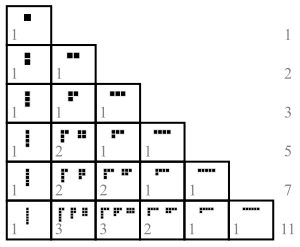
В теории чисел и комбинаторике разбиение , неотрицательного целого числа n также называемое целочисленным разбиением , представляет собой способ записи n в виде суммы положительных целых чисел . Две суммы, отличающиеся только порядком слагаемых, считаются одним и тем же разбиением. (Если порядок имеет значение, сумма становится композицией . ) Например, число 4 можно разделить пятью различными способами:

4

3 + 1

2 + 2

2 + 1 + 1

1 + 1 + 1 + 1

Единственное разбиение нуля — это пустая сумма, не имеющая частей.

Зависящая от порядка композиция 1 + 3 — это тот же раздел, что и 3 + 1 , а две разные композиции 1 + 2 + 1 и 1 + 1 + 2 представляют тот же раздел, что и 2 + 1 + 1 .

Отдельное слагаемое в разделе называется частью . Число разделов n определяется статистической суммой p ( n ) . Итак, р (4) = 5 . Обозначение λ ⊢ n означает, что λ является разбиением n .

Разделы можно графически визуализировать с помощью диаграмм Юнга или диаграмм Феррера . Они встречаются в ряде разделов математики и физики , включая изучение симметричных многочленов и симметрической группы , а также в теории представлений групп в целом.

Примеры

Семь разделов из 5

• 5
• 4 + 1
• 3 + 2
• 3 + 1 + 1
• 2 + 2 + 1
• 2 + 1 + 1 + 1
• 1 + 1 + 1 + 1 + 1

Некоторые авторы рассматривают разбиение как убывающую последовательность слагаемых, а не как выражение со знаком плюс. Например, раздел 2 + 2 + 1 вместо этого можно записать в виде кортежа (2, 2, 1) или в еще более компактной форме (2 ² , 1) где верхний индекс указывает количество повторений детали.

Это обозначение кратности для раздела можно альтернативно записать как $1^{m_{1}}2^{m_{2}}3^{m_{3}}\cdots$, где m ₁ — количество единиц, m ₂ — количество двоек и т. д. (Компоненты с m _i = 0 можно опускать.) Например, в этих обозначениях разбиения из 5 записываются $5^{1},1^{1}4^{1},2^{1}3^{1},1^{2}3^{1},1^{1}2^{2},1^{3}2^{1}$, и $1^{5}$.

Схематические изображения перегородок

Существует два распространенных схематических метода представления разделов: диаграммы Феррера, названные в честь Нормана Маклеода Феррерса , и диаграммы Янга, названные в честь Альфреда Янга . Оба имеют несколько возможных соглашений; здесь мы используем английскую систему обозначений , при этом диаграммы выравниваются по левому верхнему углу.

Диаграмма Феррера

Раздел 6+4+3+1 числа 14 можно представить следующей схемой:

14 кругов выстроены в 4 ряда, каждый размером с часть перегородки. Схемы 5-ти перегородок номера 4 показаны ниже:

4	=	3 + 1	=	2 + 2	=	2 + 1 + 1	=	1 + 1 + 1 + 1

Диаграмма Янга

Основная статья: Диаграмма Янга

Альтернативным визуальным представлением целочисленного раздела является его диаграмма Юнга (часто также называемая диаграммой Феррера). Вместо того, чтобы представлять разбиение точками, как на диаграмме Феррера, на диаграмме Янга используются прямоугольники или квадраты. Таким образом, диаграмма Юнга для разбиения 5 + 4 + 1 имеет вид

в то время как диаграмма Феррера для того же раздела имеет вид

Хотя этот, казалось бы, тривиальный вариант не заслуживает отдельного упоминания, диаграммы Юнга оказываются чрезвычайно полезными при изучении симметричных функций и теории представления групп : заполнение ячеек диаграмм Юнга числами (или иногда более сложными объектами), подчиняющимися различным правилам. приводит к семейству объектов, называемых таблицами Юнга , и эти таблицы имеют комбинаторное и теоретико-представление значение. , представляющий собой тип фигуры, состоящей из соединенных вместе соседних квадратов Диаграммы Юнга представляют собой особый вид полимино .

Функция разделения

Использование метода Эйлера для нахождения p (40): линейка со знаками плюс и минус (серый прямоугольник) перемещается вниз, соответствующие части добавляются или вычитаются. Положения знаков задаются разностью чередующихся натуральных (синих) и нечетных (оранжевых) чисел. В файле SVG наведите указатель мыши на изображение, чтобы переместить линейку.

Основная статья: Статистическая сумма (теория чисел)

Функция разделения $p(n)$ подсчитывает части неотрицательного целого числа $n$. Например, $p(4)=5$ потому что целое число $4$ имеет пять разделов $1+1+1+1$, $1+1+2$, $1+3$, $2+2$, и $4$.Значения этой функции для $n=0,1,2,\dots$ являются:

1, 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, 135, 176, 231, 297, 385, 490, 627, 792, 1002, 1255, 1575, 1958, 2436, 3010, 3718, 4565, 5604, ... (последовательность A000041 в OEIS ).

функция Производящая ​ $p$ является

$\sum _{n=0}^{\infty }p(n)q^{n}=\prod _{j=1}^{\infty }\sum _{i=0}^{\infty }q^{ji}=\prod _{j=1}^{\infty }(1-q^{j})^{-1}.$

асимптотические Выражение в замкнутой форме для статистической суммы неизвестно, но оно имеет как разложения , которые точно аппроксимируют ее, так и рекуррентные соотношения, с помощью которых ее можно точно вычислить. Он растет как экспоненциальная функция квадратного корня из своего аргумента. следующее:

$p(n)\sim {\frac {1}{4n{\sqrt {3}}}}\exp \left({\pi {\sqrt {\frac {2n}{3}}}}\right)$ как $n\to \infty$

В 1937 году Ганс Радемахер нашел способ представить статистическую сумму. $p(n)$ сходящимся рядом

$$p(n)={\frac {1}{\pi {\sqrt {2}}}}\sum _{k=1}^{\infty }A_{k}(n){\sqrt {k}}\cdot {\frac {d}{dn}}\left({{\frac {1}{\sqrt {n-{\frac {1}{24}}}}}\sinh \left[{{\frac {\pi }{k}}{\sqrt {{\frac {2}{3}}\left(n-{\frac {1}{24}}\right)}}}\,\,\,\right]}\right)$$

где

$$A_{k}(n)=\sum _{0\leq m<k,\;(m,k)=1}e^{\pi i\left(s(m,k)-2nm/k\right)}.$$

и $s(m,k)$ есть сумма Дедекинда .

Мультипликативная обратная производящая функция — это функция Эйлера ; Эйлера по теореме о пятиугольных числах эта функция представляет собой знакопеременную сумму степеней пятиугольных чисел своего аргумента.

$p(n)=p(n-1)+p(n-2)-p(n-5)-p(n-7)+\cdots$

Шриниваса Рамануджан обнаружил, что статистическая сумма имеет нетривиальные закономерности в модульной арифметике , известные теперь как сравнения Рамануджана . Например, всякий раз, когда десятичное представление $n$ заканчивается на цифру 4 или 9, количество разделов $n$ будет делиться на 5.

Ограниченные разделы

И в комбинаторике, и в теории чисел часто изучаются семейства разбиений, на которые распространяются различные ограничения. В этом разделе рассматриваются некоторые такие ограничения.

Сопряженные и самосопряженные разделы

Если перевернуть схему разбиения 6 + 4 + 3 + 1 вдоль его главной диагонали, то получим еще одно разбиение из 14:

	↔
6 + 4 + 3 + 1	=	4 + 3 + 3 + 2 + 1 + 1

Превратив строки в столбцы, мы получим разбиение 4 + 3 + 3 + 2 + 1 + 1 числа 14. Такие разбиения называются сопряженными друг другу. В случае числа 4 разбиения 4 и 1+1+1+1 являются сопряженными парами, а разбиения 3+1 и 2+1+1 сопряжены друг другу. Особый интерес представляют разбиения, например 2+2, которые сами по себе являются сопряженными. Такие разбиения называются самосопряженными .

Утверждение : количество самосопряженных разделов равно количеству разделов с различными нечетными частями.

Доказательство (схема) : Важнейшее наблюдение состоит в том, что каждую нечетную часть можно « сложить » посередине, чтобы сформировать самосопряженную диаграмму:

↔

Затем можно получить биекцию между набором разделов с различными нечетными частями и набором самосопряженных разделов, как иллюстрируется следующим примером:

	↔
9 + 7 + 3	=	5 + 5 + 4 + 3 + 2
Расст. странный		самосопряженный

Нечетные и отдельные части

Среди 22 разделов числа 8 есть 6, которые содержат только нечетные части :

• 7 + 1
• 5 + 3
• 5 + 1 + 1 + 1
• 3 + 3 + 1 + 1
• 3 + 1 + 1 + 1 + 1 + 1
• 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1

В качестве альтернативы мы могли бы подсчитать разделы, в которых ни одно число не встречается более одного раза. Такой раздел называется разделом, состоящим из отдельных частей . Если посчитать разбиения 8 на отдельные части, то тоже получим 6:

• 8
• 7 + 1
• 6 + 2
• 5 + 3
• 5 + 2 + 1
• 4 + 3 + 1

Это общее свойство. Для каждого положительного числа количество разделов с нечетными частями равно количеству разделов с различными частями, обозначаемому q ( n ). Этот результат был доказан Леонардом Эйлером в 1748 году. и позже была обобщена как теорема Глейшера .

Для каждого типа ограниченного раздела существует соответствующая функция количества разделов, удовлетворяющих данному ограничению. Важным примером является q ( n ) (разделение на отдельные части). Первые несколько значений q ( n ) (начиная с q (0)=1):

1, 1, 1, 2, 2, 3, 4, 5, 6, 8, 10, ... (последовательность A000009 в OEIS ).

для Производящая функция q ( n ) определяется выражением

$\sum _{n=0}^{\infty }q(n)x^{n}=\prod _{k=1}^{\infty }(1+x^{k})=\prod _{k=1}^{\infty }{\frac {1}{1-x^{2k-1}}}.$

Теорема о пятиугольных числах дает возврат для q :

q ( ​​k ) знак равно a _k + q ( k - 1) + q ( k - 2) - q ( k - 5) - q ( k - 7) + q ( k - 12) + q ( k - 15) - q ( ​​k − 22) − ...

где a _k равно (−1) ^м если к = 3 м ² − m для некоторого целого числа m и равно 0 в противном случае.

Ограниченный размер или количество деталей

Основная статья: Треугольник номеров разделов

Если взять сопряженные числа, то количество p _k ( n ) разбиений n ровно на k частей равно количеству разбиений n, в которых наибольшая часть имеет размер k . Функция p _k ( n ) удовлетворяет рекуррентному правилу

п _k ( п ) знак равно п _k ( п - k ) + п _{k -1} ( п - 1)

с начальными значениями p ₀ (0) = 1 и p _k ( n ) = 0, если n ≤ 0 или k ≤ 0 и n и k не равны нулю.

Функцию p ( n ) можно восстановить с помощью

$p(n)=\sum _{k=0}^{n}p_{k}(n).$

Одна из возможных производящих функций для таких разделов при фиксированном k и переменной n :

$\sum _{n\geq 0}p_{k}(n)x^{n}=x^{k}\prod _{i=1}^{k}{\frac {1}{1-x^{i}}}.$

В более общем смысле, если T — набор положительных целых чисел, то количество разделов n , все части которых принадлежат T , имеет производящую функцию

$\prod _{t\in T}(1-x^{t})^{-1}.$

Это можно использовать для решения проблем с внесением сдачи (где набор T указывает доступные монеты). В качестве двух частных случаев можно отметить, что количество разбиений n , в которых все части равны 1 или 2 (или, что то же самое, количество разбиений n на 1 или 2 части), равно

$\left\lfloor {\frac {n}{2}}+1\right\rfloor ,$

а количество разбиений n, в которых все части равны 1, 2 или 3 (или, что то же самое, количество разбиений n не более чем на три части), является ближайшим к ( n + 3) целым числом. ² / 12.

Разбиения в прямоугольнике и

Основная статья: Биномиальный коэффициент Гаусса

Также можно одновременно ограничить количество и размер деталей. Пусть p ( N , M ; n ) обозначает количество разбиений n не более чем на M частей, каждая из которых имеет размер не более N . Эквивалентно, это разбиения, диаграмма Юнга которых помещается внутри M × N. прямоугольника Существует рекуррентное соотношение

$$p(N,M;n)=p(N,M-1;n)+p(N-1,M;n-M)$$

получено, наблюдая, что $p(N,M;n)-p(N,M-1;n)$ подсчитывает разбиения n ровно на M частей размером не более N , а вычитание 1 из каждой части такого разбиения дает разбиение n - M не более чем на M частей.

Биномиальный коэффициент Гаусса определяется как:

$${k+\ell \choose \ell }_{q}={k+\ell \choose k}_{q}={\frac {\prod _{j=1}^{k+\ell }(1-q^{j})}{\prod _{j=1}^{k}(1-q^{j})\prod _{j=1}^{\ell }(1-q^{j})}}.$$

Биномиальный коэффициент Гаусса связан с производящей функцией p ( N , M ; n ) равенством

$$\sum _{n=0}^{MN}p(N,M;n)q^{n}={M+N \choose M}_{q}.$$

и

Основная статья: Площадь Дерфи

Ранг k раздела — это наибольшее число такое , что раздел содержит не менее k частей размером не менее k . Например, разбиение 4 + 3 + 3 + 2 + 1 + 1 имеет ранг 3, поскольку оно содержит 3 части с числом ≥ 3, но не содержит 4 частей с числом ≥ 4. В диаграмме Феррера или диаграмме Юнга разбиения ранга r квадрат r × r записей в левом верхнем углу известен как квадрат Дерфи :

Квадрат Дёрфи находит применение в комбинаторике для доказательства различных тождеств разбиения. Он также имеет некоторое практическое значение в виде индекса Хирша .

(или рангом Дайсона) иногда называют и другую статистику Рангом разбиения , а именно разность $\lambda _{k}-k$ для разбиения из k частей с наибольшей частью $\lambda _{k}$. Эта статистика (не имеющая отношения к описанной выше) появляется при изучении сравнений Рамануджана .

Решетка Янга

Основная статья: Решетка Юнга

На разбиениях существует естественный частичный порядок , задаваемый включением диаграмм Юнга. Этот частично упорядоченный набор известен как решетка Юнга . Решетка была первоначально определена в контексте теории представлений где она используется для описания неприводимых представлений симметрических групп Sn _n для всех , вместе с их свойствами ветвления в нулевой характеристике. Его чисто комбинаторные свойства также подверглись серьезному изучению; в частности, это мотивирующий пример дифференциального ЧУУ .

Случайные разделы

Существует глубокая теория случайных разбиений, выбранных в соответствии с равномерным распределением вероятностей на симметричной группе посредством соответствия Робинсона-Шенстеда . В 1977 году Логан и Шепп, а также Вершик и Керов показали, что диаграмма Юнга типичного большого разбиения становится асимптотически близкой к графику некоторой аналитической функции, минимизирующей некоторый функционал. В 1988 году Байк, Дейфт и Йоханссон расширили эти результаты, чтобы определить распределение самой длинной возрастающей подпоследовательности случайной перестановки с точки зрения распределения Трейси – Уидома . Окуньков связал эти результаты с комбинаторикой римановых поверхностей и теорией представлений.

См. также

• Ранг раздела , другое понятие ранга
• Рукоятка перегородки
• Порядок доминирования
• Факторизация
• Целочисленная факторизация
• Раздел набора
• Звезды и полосы (комбинаторика)
• Плоская перегородка
• Вежливое число , определяемое делением на последовательные целые числа.
• Мультипликативный раздел
• Двенадцатикратный путь
• Формула выборки Юэнса
• Получить формулу Бруно
• Многораздельность
• Личности Ньютона
• Функция наименьших деталей
• Разделение Гольдбаха — это разбиение четного числа на простые числа (см. гипотезу Гольдбаха ).
• Статистическая сумма Костанта

Ссылки

• Абрамовиц, Милтон ; Стегун, Ирен (1964). Справочник по математическим функциям с формулами, графиками и математическими таблицами . Министерство торговли США, Национальное бюро стандартов. ISBN  0-486-61272-4 .
• Эндрюс, Джордж Э. (1976). Теория разделов . Издательство Кембриджского университета. ISBN  0-521-63766-Х .
• Эндрюс, Джордж Э.; Эрикссон, Киммо (2004). Целочисленные разделы . Издательство Кембриджского университета. ISBN  0-521-60090-1 .
• Апостол, Том М. (1990) [1976]. Модульные функции и ряды Дирихле в теории чисел . Тексты для аспирантов по математике . Том. 41 (2-е изд.). Нью-Йорк и др.: Springer-Verlag . ISBN  0-387-97127-0 . Збл   0697.10023 . (См. главу 5, где представлено современное педагогическое введение в формулу Радемахера) .
• Бона, Миклош (2002). Прогулка по комбинаторике: введение в перечисление и теорию графов . Мировое научное издательство. ISBN  981-02-4900-4 . (элементарное введение в тему целочисленных разделов, включая обсуждение графов Феррера)
• Харди, штат Джорджия ; Райт, Э.М. (2008) [1938]. Введение в теорию чисел . Под редакцией Д. Р. Хита-Брауна и Дж. Х. Сильвермана . Предисловие Эндрю Уайлса . (6-е изд.). Оксфорд: Издательство Оксфордского университета . ISBN  978-0-19-921986-5 . МР   2445243 . Збл   1159.11001 .
• Лемер, Д.Х. (1939). «Об остатке и сходимости ряда для статистической суммы» . Пер. амер. Математика. Соц . 46 : 362–373. дои : 10.1090/S0002-9947-1939-0000410-9 . МР   0000410 . Збл   0022.20401 . Предоставляет основную формулу (без производных), остаток и старую форму для A _k ( n ).)
• Гупта, Хансрадж; Гвитер, CE; Миллер, JCP (1962). Королевское математическое общество. Таблицы . Том. 4. Таблицы разделов. (Есть текст, почти полная библиография, но они (и Абрамовиц) пропустили формулу Сельберга для A _k ( n ), которая есть у Уайтмена.)
• Макдональд, Ян Г. (1979). Симметричные функции и полиномы Холла . Оксфордские математические монографии. Издательство Оксфордского университета . ISBN  0-19-853530-9 . Збл   0487.20007 . (См. раздел I.1)
• Натансон, МБ (2000). Элементарные методы теории чисел . Тексты для аспирантов по математике. Том. 195. Шпрингер-Верлаг . ISBN  0-387-98912-9 . Збл   0953.11002 .
• Радемахер, Ганс (1974). Сборник статей Ганса Радемахера . Том v II. MIT Press. стр. 100–07, 108–22, 460–75.
• Сотой, Маркус Дю. (2003). Музыка простых чисел . Нью-Йорк: Perennial-HarperCollins. ISBN  9780066210704 .
• Стэнли, Ричард П. (1999). Перечислительная комбинаторика . Том. 1 и 2. Издательство Кембриджского университета. ISBN  0-521-56069-1 .
• Уайтмен, Алабама (1956). «Сумма, связанная с рядом для статистической суммы» . Тихоокеанский математический журнал . 6 (1): 159–176. дои : 10.2140/pjm.1956.6.159 . Збл   0071.04004 . (Обеспечивает формулу Сельберга. Более старая форма - это конечное разложение Фурье Сельберга.)

Внешние ссылки

• «Разбиение» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Калькулятор разделов и составов
• Вайсштейн, Эрик В. «Перегородка» . Математический мир .
• Уилф, Герберт С. Лекции по целочисленным разбиениям (PDF) , заархивировано (PDF) из оригинала 24 февраля 2021 г. , получено 28 февраля 2021 г.
• Счет с разбиениями со ссылками на таблицы в Электронной энциклопедии целочисленных последовательностей.
• Запись о целочисленных разделах в FindStat базе данных
• Модуль Integer::Partition Perl из CPAN
• Быстрые алгоритмы создания целочисленных разделов
• Генерация всех разделов: сравнение двух кодировок
• Грайм, Джеймс (28 апреля 2016 г.). «Перегородки — Числофил» (видео) . Брэйди Харан . Архивировано из оригинала 11 декабря 2021 г. Проверено 5 мая 2016 г.