Сет (музыка)

Набор набор ( высоты тона , набор классов высоты , класс набора , форма набора , род набора , набор высоты тона ) в теории музыки , как и в математике и в общем языке, представляет собой совокупность объектов. В музыкальных контекстах этот термин традиционно применяется чаще всего к наборам высот или высотных классов , но теоретики распространили его использование на другие типы музыкальных объектов, так что можно говорить о наборах длительностей или тембров . , например, [2]
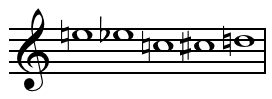

Набор сам по себе не обязательно обладает какой-либо дополнительной структурой, такой как упорядочение или перестановка . Тем не менее, с музыкальной точки зрения часто важно рассматривать наборы, оснащенные отношением порядка (называемые сегментами ); в таких контекстах голые наборы для большей выразительности часто называют «неупорядоченными». [4]
Наборы из двух элементов называются диадами , наборы из трех элементов — трихордами (иногда «триадами», хотя это легко спутать с традиционным значением слова «триада »). Наборы высших мощностей называются тетрахордами (или тетрадами), пентахордами (или пентадами), гексахордами (или гексадами), гептахордами (септахордами или, иногда, смешением латинского и греческого корней, «септахордами»), [5] октахорды (октады), нонахорды (нонады), декашорды (декады), ундекахорды и, наконец, додекахорды .
Набор временных точек — это набор длительности , в котором расстояние в единицах времени между точками атаки или временными точками представляет собой расстояние в полутонах между классами высоты тона. [6]
Серийный
[ редактировать ]Однако в теории серийной музыки некоторые авторы [ ласковые слова ] (особенно Милтон Бэббит [7] [ нужна страница ] [ нужна цитата для проверки ] ) используют термин «набор» там, где другие использовали бы «ряд» или «серию», а именно для обозначения упорядоченного набора (например, двенадцатитонового ряда ), используемого для структурирования произведения. Эти авторы [ ласковые слова ] говорят о «двенадцати наборах тонов», «наборах моментов времени», «производных наборах» и т. д. (См. ниже.) Это использование термина «набор», отличное от описанного выше (и упоминаемого в термине «набор»). теория множеств »).
Для этих авторов [ ласковые слова ] форма набора (или форма строки ) — это особое расположение такого упорядоченного набора: простая форма (исходный порядок), инверсная (перевернутая), ретроградная (назад) и ретроградная инверсная (назад и вверх ногами). [2]
Производный набор — это тот, который генерируется или выводится из последовательных операций над подмножеством, например, , Веберна Концерт соч. 24, в котором последние три подмножества являются производными от первого: [8]
Это можно представить численно как целые числа от 0 до 11:
0 11 3 4 8 7 9 5 6 1 2 10
Первое подмножество (BB ♭ D):
0 11 3 prime-form, interval-string = ⟨−1 +4⟩
Второй подмножество (E ♭ GF ♯ ), являющееся ретроградной инверсией первого, транспонировано на один полутон вверх:
3 11 0 retrograde, interval-string = ⟨−4 +1⟩ mod 12 3 7 6 inverse, interval-string = ⟨+4 −1⟩ mod 12 + 1 1 1 ------ = 4 8 7
Третий подмножество (G ♯ EF), являющееся ретроградным по отношению к первому, транспонировано вверх (или вниз) на шесть полутонов:
3 11 0 retrograde + 6 6 6 ------ 9 5 6
И четвертый подмножество (CC ♯ A), являющееся инверсией первого, транспонировано на один полутон вверх:
0 11 3 prime form, interval-vector = ⟨−1 +4⟩ mod 12 0 1 9 inverse, interval-string = ⟨+1 −4⟩ mod 12 + 1 1 1 ------- 1 2 10
Таким образом, каждый из четырех трихордов (наборов из трех нот) отображает взаимосвязь, которую можно сделать очевидной с помощью любой из четырех операций последовательного ряда, и, таким образом, создает определенные инварианты . Эти неизменности в серийной музыке аналогичны использованию общих тонов и общих аккордов в тональной музыке. [ нужна ссылка ]
Несерийный
[ редактировать ]


Фундаментальная концепция непоследовательного набора заключается в том, что он представляет собой неупорядоченный набор классов высоты тона . [9]
Нормальная форма набора — это наиболее компактное упорядочение звуков в наборе. [10] Томлин определяет «самый компактный» порядок как тот, при котором «самый большой из интервалов между любыми двумя последовательными шагами находится между первым и последним из перечисленных шагов». [10] Например, набор (0,2) ( большая секунда ) находится в нормальной форме, а набор (0,10) ( малая седьмая часть , инверсия большой секунды) — нет, его нормальная форма равна (10,0 ).
Вместо «исходной» (нетранспонированной, неинвертированной) формы набора, простую форму можно считать либо нормальной формой набора, либо нормальной формой его инверсии, в зависимости от того, какая из них более плотно упакована. [11] Форте (1973) и Ран (1980) называют простые формы множества наиболее левоупакованными из возможных версий множества. Форте упаковывает слева, а Ран упаковывает справа («уменьшая маленькие числа» вместо «уменьшая большие числа... меньшими»). [12] ). В течение многих лет считалось, что существует только пять случаев, когда эти два алгоритма различаются. [13] Однако в 2017 году теоретик музыки Ян Ринг обнаружил, что существует шестой класс множеств, в котором алгоритмы Форте и Рана приходят к разным простым формам. [14] Ян Ринг также разработал гораздо более простой алгоритм вычисления простой формы множества: [14] который дает те же результаты, что и более сложный алгоритм, ранее опубликованный Джоном Раном.
Векторы
[ редактировать ]См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Уиттолл, Арнольд (2008). Кембриджское введение в сериализм , стр.165. Нью-Йорк: Издательство Кембриджского университета. ISBN 978-0-521-68200-8 (пбк).
- ^ Перейти обратно: а б Виттлих, Гэри (1975). «Наборы и процедуры упорядочения в музыке двадцатого века», «Аспекты музыки двадцатого века» , стр.475. Виттлих, Гэри (ред.). Энглвуд Клиффс, Нью-Джерси: Прентис-Холл. ISBN 0-13-049346-5 .
- ^ Уиттолл (2008), стр.127.
- ^ Моррис, Роберт (1987). Композиция с высотой тона: теория композиционного дизайна , стр.27. Издательство Йельского университета. ISBN 0-300-03684-1 .
- ^ Например, Ран (1980), 140.
- ^ Виттлих (1975), стр.476.
- ↑ См. любые его сочинения о двенадцатитоновой системе, практически все из которых перепечатаны в «Сборнике эссе Милтона Бэббита» , С. Пелеса и др., под ред. Издательство Принстонского университета, 2003. ISBN 0-691-08966-3 .
- ^ Виттлих (1975), стр.474.
- ^ Джон Ран , Основная атональная теория (Нью-Йорк: Лонгман; Лондон и Торонто: Prentice Hall International, 1980), стр. 27–28. ISBN 0-582-28117-2 (Лонгман); ISBN 0-02-873160-3 (Prentice Hall International). Перепечатано в 1987 г. (Нью-Йорк: Schirmer Books; Лондон: Collier Macmillan, 1980), стр.27. ISBN 0-02-873160-3 .
- ^ Перейти обратно: а б Томлин, Джей. «Все о теории множеств: что такое нормальная форма?» , ДжейТомлин.com .
- ^ Томлин, Джей. «Все о теории множеств: что такое простая форма?» , ДжейТомлин.com .
- ^ Нельсон, Пол (2004). «Два алгоритма вычисления простой формы» . ComposerTools.com . Архивировано из оригинала 23 декабря 2017 года.
{{cite web}}: CS1 maint: неподходящий URL ( ссылка ) - ^ Цао, Мин (2007). Абстрактные музыкальные интервалы: теория групп для композиции и анализа , стр.99, №32. ISBN 9781430308355 . Алгоритмы приведены в книге Моррис, Роберт (1991). Конспекты занятий по теории атональной музыки , стр.103. Музыка Лягушачьего Пика.
- ^ Перейти обратно: а б «Этюд музыкальных гамм Яна Ринга» .
Дальнейшее чтение
[ редактировать ]- Шуйер, Михель (2008). Анализ атональной музыки: теория множеств высоты звука и ее контексты . ISBN 978-1-58046-270-9 .
Внешние ссылки
[ редактировать ]- «Калькулятор теории множеств» , JayTomlin.com . Вычисляет нормальную форму, простую форму, число Форте и вектор интервального класса для заданного набора и наоборот.
- « Калькулятор ПК , MtA.Ca. »
