Сумматор (электроника)

Суммар лето или , , ^[1] представляет собой цифровую схему , выполняющую сложение чисел. Во многих компьютерах и других типах процессоров сумматоры используются в арифметико-логических устройствах (АЛУ). Они также используются в других частях процессора, где используются для вычисления адресов , индексов таблиц , операторов увеличения и уменьшения и подобных операций.

Хотя сумматоры могут быть созданы для многих представлений чисел , таких как двоично-десятичное число или избыточное число-3 , наиболее распространенные сумматоры работают с двоичными числами .В тех случаях, когда дополнение до двух или дополнение до единиц используется для представления отрицательных чисел , преобразовать сумматор в сумматор-вычитатель тривиально .Другие представления чисел со знаком требуют больше логики вокруг базового сумматора.

История [ править ]

Джордж Стибиц изобрел 2-битный двоичный сумматор ( модель К ) в 1937 году.

Двоичные суммы [ править ]

Полусумматор [ править ]

Полусумматор . складывает две одиночные двоичные цифры $A$ и $B$ . Он имеет два выхода: sum ( $S$ ) и нести ( $C$ ). Сигнал переноса представляет собой переполнение следующей цифры многозначного сложения. Значение суммы $2C+S$ . Самая простая конструкция полусумматора, изображенная справа, включает в себя логический элемент исключающее ИЛИ для $S$ и вентиль И для $C$ . Булева логика суммы (в данном случае $S$ ) будет $A\oplus B$ тогда как для переноса ( $C$ ) будет $A\cdot B$ . С добавлением логического элемента ИЛИ для объединения выходов переноса два полусумматора можно объединить в полный сумматор. ^[2] Полусумматор складывает два входных бита и генерирует перенос и сумму, которые являются двумя выходами полусумматора. Входные переменные полусумматора называются битами добавления и сложения. Выходными переменными являются сумма и перенос.

Таблица истинности для полусумматора:

Входы		Выходы
А	Б	C _выход	С
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

Различные цифровые логические схемы с полусумматором:

Полусумматор в действии.
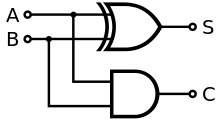
Схема полусумматора, реализованная с одним логическим элементом XOR и одним логическим элементом AND .
Схема полусумматора, реализованного с пятью вентилями И-НЕ .
Схематическое обозначение 1-битного полусумматора.

Полный сумматор [ править ]

Полный сумматор складывает двоичные числа и учитывает входящие и исходящие значения. Однобитный полный сумматор складывает три однобитных числа, часто записываемых как $A$ , $B$ , и $C_{in}$ ; $A$ и $B$ являются операндами, и $C_{in}$ немного перенесен с предыдущего, менее значимого этапа. ^[3] Полный сумматор обычно является компонентом каскада сумматоров, которые складывают 8, 16, 32 и т. д. битные двоичные числа. Схема выдает двухбитовый выходной сигнал. Выходной перенос и сумма обычно представляются сигналами $C_{out}$ и $S$ , где сумма равна $2C_{out}+S$ .

Полный сумматор можно реализовать разными способами, например, с помощью специальной схемы транзисторного уровня или состоящей из других вентилей. Наиболее распространенная реализация:

S=A\oplus B\oplus C_{in}

C_{out}=(A\cdot B)+(C_{in}\cdot (A\oplus B))

Приведенные выше выражения для $S$ и $C_{in}$ может быть получена с помощью карты Карно для упрощения таблицы истинности.

В этой реализации последний логический элемент ИЛИ перед выходным сигналом переноса может быть заменен логическим элементом исключающее ИЛИ без изменения результирующей логики. Это потому, что когда A и B оба равны 1, член $(A\oplus B)$ всегда 0, и, следовательно, $(C_{in}\cdot (A\oplus B))$ может быть только 0. Таким образом, входы последнего элемента ИЛИ никогда не могут быть одновременно 1 (это единственная комбинация, для которой выходы ИЛИ и XOR различаются).

Благодаря свойству функциональной полноты вентилей И-НЕ и ИЛИ-НЕ, полный сумматор также может быть реализован с использованием девяти вентилей И-НЕ . ^[4] или девять ворот NOR .

Использование только двух типов вентилей удобно, если схема реализуется с использованием простых интегральных микросхем, которые содержат только один тип вентилей на кристалл.

Полный сумматор можно составить и из двух полусумматоров, соединив $A$ и $B$ на вход одного полусумматора, затем принимая его сумму на выходе $S$ в качестве одного из входов второго полусумматора и $C_{in}$ в качестве другого входа, и, наконец, выходы переноса двух полусумматоров подключаются к логическому элементу ИЛИ. Сумма на выходе второго полусумматора является окончательной суммой на выходе ( $S$ ) полного сумматора, а выходной сигнал логического элемента ИЛИ является конечным выходом переноса ( $C_{out}$ ). Критический путь полного сумматора проходит через оба вентиля XOR и заканчивается в бите суммы. $S$ . Предполагая, что для завершения вентиля XOR требуется 1 задержка, задержка, вызванная критическим путем полного сумматора, равна:

T_{\text{FA}}=2\cdot T_{\text{XOR}}=2D

Критический путь переноса проходит через один логический элемент «ИСКЛЮЧАЮЩЕЕ ИЛИ» в сумматоре и через 2 логических элемента (И и ИЛИ) в блоке переноса, и поэтому, если для завершения логических элементов «И» или «ИЛИ» требуется 1 задержка, задержка составит:

T_{\text{c}}=T_{\text{XOR}}+T_{\text{AND}}+T_{\text{OR}}=D+D+D=3D

Таблица истинности для полного сумматора:

Входы			Выходы
А	Б	С _в	C _выход	С
0	0	0	0	0
0	0	1	0	1
0	1	0	0	1
0	1	1	1	0
1	0	0	0	1
1	0	1	1	0
1	1	0	1	0
1	1	1	1	1

Инвертирование всех входов полного сумматора также инвертирует все его выходы, что можно использовать при разработке быстрых сумматоров с пульсирующим переносом, поскольку нет необходимости инвертировать перенос. ^[5]

Различные цифровые логические схемы с полным сумматором:

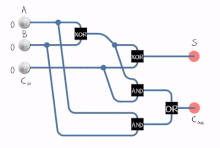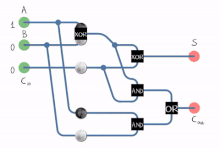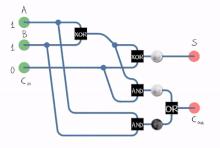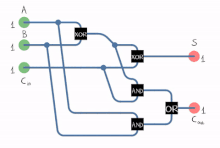
Полный сумматор в действии.
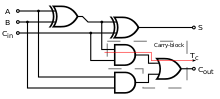
Схема полного сумматора, реализованная с двумя логическими элементами исключающее ИЛИ , двумя логическими элементами И и одним логическим элементом ИЛИ .
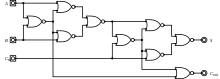
Схема полного сумматора, реализованного с девятью вентилями И-НЕ .
Схема полного сумматора, реализованного с девятью вентилями ИЛИ .
Полный сумматор с инвертированными выходами и однотранзисторной задержкой распространения переноса в КМОП ^[5]
Схематический символ 1-битного полного сумматора с C _входом и C, _{выходом} нарисованными по бокам блока, чтобы подчеркнуть их использование в многобитном сумматоре.

поддерживающие несколько битов , Сумматоры

Сумматор с пульсирующим переносом [ править ]

Десятичный четырехзначный сумматор с пульсирующим переносом. FA = полный сумматор, HA = полусумматор.

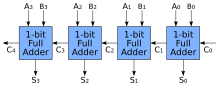
Можно создать логическую схему, используя несколько полных сумматоров для сложения N -битных чисел. Каждый полный сумматор вводит $C_{in}$ , который является $C_{out}$ предыдущего сумматора. Этот тип сумматора называется сумматором со пульсирующим переносом (RCA), поскольку каждый бит переноса «переносится» к следующему полному сумматору. Первый (и только первый) полный сумматор можно заменить полусумматором (при условии, что $C_{in}=0$ ).

Схема сумматора с пульсирующим переносом проста, что позволяет сократить время проектирования; однако сумматор со пульсирующим переносом работает относительно медленно, поскольку каждый полный сумматор должен ожидать вычисления бита переноса на основе предыдущего полного сумматора. Задержку вентиля можно легко рассчитать, проверив полную схему сумматора. Каждый полный сумматор требует трех уровней логики. В 32-битном сумматоре со пульсирующим переносом имеется 32 полных сумматора, поэтому задержка критического пути (наихудший случай) равна 3 (от входа до переноса в первом сумматоре) + 31 × 2 (для распространения переноса в последних сумматорах) = 65 задержки на воротах. ^[6]Общее уравнение для наихудшего случая задержки для n- битного сумматора с пульсациями переноса, учитывающее как сумму, так и биты переноса, выглядит следующим образом:

T_{\text{CRA}}(n)=T_{\text{HA}}+(n-1)\cdot T_{\text{c}}+T_{\text{s}}=

T_{\text{FA}}+(n-1)\cdot T_{c}=

3D+(n-1)\cdot 2D=(2n+1)\cdot D

Конструкция с переменной полярностью переноса и оптимизированными вентилями И-ИЛИ-Инверт может работать примерно в два раза быстрее. ^[7]^[5]

Сумматор с переносом вперед [ править ]

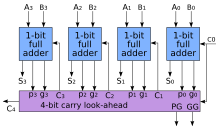
Чтобы сократить время вычислений, инженеры разработали более быстрые способы сложения двух двоичных чисел с помощью сумматоров с упреждающим переносом (CLA). Они работают, создавая два сигнала ( $P$ и $G$ ) для каждой битовой позиции, в зависимости от того, распространяется ли перенос из менее значимой битовой позиции (по крайней мере, один вход имеет значение 1), генерируется в этой битовой позиции (оба входных сигнала равны 1) или уничтожается в этой битовой позиции (оба входы 0). В большинстве случаев $P$ это просто сумма на выходе полусумматора и $G$ — выход переноса того же сумматора. После $P$ и $G$ генерируются, создаются переносы для каждой битовой позиции. Некоторые продвинутые архитектуры с упреждающим переносом — это манчестерская цепочка переноса , сумматор Брента-Кунга (BKA), ^[8] и сумматор Когге – Стоуна (KSA). ^[9]^[10]

Некоторые другие архитектуры многобитных сумматоров разбивают сумматор на блоки. Можно изменять длину этих блоков в зависимости от задержки распространения цепей, чтобы оптимизировать время вычислений. Эти блочные сумматоры включают в себя сумматор с пропуском переноса (или обходом переноса), который будет определять $P$ и $G$ значения для каждого блока, а не для каждого бита, и сумматор выбора переноса , который предварительно генерирует сумму и значения переноса для любого возможного входа переноса (0 или 1) в блок, используя мультиплексоры для выбора соответствующего результата, когда бит переноса известно.

Объединив несколько сумматоров с переносом вперед, можно создать еще более крупные сумматоры. Это можно использовать на нескольких уровнях для создания еще более крупных сумматоров. Например, следующий сумматор представляет собой 64-битный сумматор, который использует четыре 16-битных CLA с двумя уровнями блоков прогнозируемого переноса .

Другие конструкции сумматора включают сумматор с выбором переноса , сумматор условной суммы , сумматор с пропуском переноса и сумматор с полным переносом.

Сумматоры переноса-сохранения [ править ]

Если схема сложения предназначена для вычисления суммы трех или более чисел, может оказаться выгодным не распространять результат переноса. Вместо этого используются трехвходовые сумматоры, генерирующие два результата: сумму и перенос. Сумма и перенос могут быть поданы на два входа последующего трехзначного сумматора, не дожидаясь распространения сигнала переноса. Однако после всех этапов сложения необходимо использовать обычный сумматор (такой как пульсирующий перенос или просмотр вперед) для объединения окончательной суммы и результатов переноса.

Компрессоры 3:2 [ править ]

Полный сумматор можно рассматривать как компрессор с потерями 3:2 : он суммирует три однобитных входных сигнала и возвращает результат в виде одного двухбитного числа; то есть он отображает 8 входных значений в 4 выходных значения. Так, например, двоичный ввод 101 приводит к выводу 1 + 0 + 1 = 10 (десятичное число 2). Выполнение представляет собой первый бит результата, а сумма представляет собой нулевой бит. Аналогичным образом, полусумматор можно использовать в качестве компрессора с потерями 2:2 , сжимая четыре возможных входных сигнала в три возможных выходных сигнала.

Такие компрессоры можно использовать для ускорения суммирования трех и более слагаемых. Если количество слагаемых равно трем, макет известен как сумматор переноса-сохранения . Если количество слагаемых равно четырем и более, необходимо более одного слоя компрессоров, и возможны различные конструкции схемы: наиболее распространенными являются Дадды и деревья Уоллеса . Этот тип схем чаще всего используется в схемах умножителей , поэтому эти схемы также известны как умножители Дадды и Уоллеса.

Квантовые сумматоры [ править ]

Используя только Тоффоли и CNOT квантовые логические элементы , можно создавать квантовые полные и полусумматоры. ^[11]^[12]^[13] Те же самые схемы могут быть реализованы и в классических обратимых вычислениях , поскольку и CNOT, и Тоффоли также являются классическими логическими вентилями .

Поскольку квантовое преобразование Фурье имеет низкую сложность схемы , его также можно эффективно использовать для сложения чисел. ^[14]^[15]

Аналоговые сумматоры [ править ]

Как и в двоичных сумматорах, объединение двух входных токов эффективно складывает эти токи. В рамках ограничений аппаратного обеспечения недвоичные сигналы (т.е. с основанием выше 2) могут складываться для вычисления суммы. Также известный как «суммирующий усилитель», ^[16] этот метод можно использовать для уменьшения количества транзисторов в дополнительной схеме.

См. также [ править ]

Двоичный множитель
вычитатель
Электронный микшер — для добавления аналоговых сигналов.

Ссылки [ править ]

^ Сингх, Аджай Кумар (2010). Проектирование цифровых СБИС . Прентис Холл Индия. п. 321. ИСБН 9788120341876 – через Google Книги.
^ Ланкастер, Джеффри А. (2004). Проектирование и разработка программного обеспечения Excel HSC . Паскаль Пресс. п. 180. ИСБН 978-1-74125175-3 .
^ Мано, М. Моррис (1979). Цифровая логика и компьютерный дизайн . Прентис-Холл . стр. 119–123 . ISBN 978-0-13-214510-7 .
^ Теджа, Рави (15 апреля 2021 г.), Схемы половинного и полного сумматора , получено 27 июля 2021 г.
^ Jump up to: Перейти обратно: ^а ^б ^с Фишер, П. «Простые схемные блоки» (PDF) . Гейдельбергский университет. Архивировано из оригинала (PDF) 5 сентября 2021 г. Проверено 05 сентября 2021 г.
^ Сатпати, Пинаки (2016). Проектирование и реализация сумматора Carry Select с использованием T-Spice . Якорное академическое издательство. п. 22. ISBN 978-3-96067058-2 .
^ Берджесс, Нил (2011). Быстрые сумматоры с пульсирующим переносом в КМОП СБИС стандартных ячеек . 20-й симпозиум IEEE по компьютерной арифметике . стр. 103–111.
^ Брент, Ричард Пирс ; Кунг, Сян Те (март 1982 г.). «Обычная схема для параллельных сумматоров» . Транзакции IEEE на компьютерах . С-31 (3): 260–264. дои : 10.1109/TC.1982.1675982 . ISSN 0018-9340 . S2CID 17348212 . Архивировано из оригинала 24 сентября 2017 года.
^ Когге, Питер Майкл ; Стоун, Гарольд С. (август 1973 г.). «Параллельный алгоритм эффективного решения общего класса рекуррентных уравнений». Транзакции IEEE на компьютерах . С-22 (8): 786–793. дои : 10.1109/TC.1973.5009159 . S2CID 206619926 .
^ Рейндерс, Неле; Деэн, Вим (2015). Проектирование энергоэффективных цифровых схем сверхнизкого напряжения . Аналоговые схемы и обработка сигналов (1-е изд.). Чам, Швейцария: Springer International Publishing AG, Швейцария . дои : 10.1007/978-3-319-16136-5 . ISBN 978-3-319-16135-8 . ISSN 1872-082X . LCCN 2015935431 .
^ Фейнман, Ричард П. (1986). «Квантово-механические компьютеры». Основы физики . 16 (6). Springer Science and Business Media LLC: 507–531. Бибкод : 1986FoPh...16..507F . дои : 10.1007/bf01886518 . ISSN 0015-9018 . S2CID 122076550 .
^ «Пример кода: квантовый полный сумматор» . QuTech (Технологический университет Делфта (TU Delft) и Нидерландская организация прикладных научных исследований (TNO)).
^ Дибьенду Чаттерджи, Ариджит Рой (2015). «Схема квантового полусумматора на основе трансмонов» . Успехи теоретической и экспериментальной физики . 2015 (9): 093А02. Бибкод : 2015PTEP.2015i3A02C . дои : 10.1093/ptep/ptv122 .
^ Дрейпер, Томас Г. (7 августа 2000 г.). «Дополнение о квантовом компьютере». arXiv : Quant-ph/0008033 .
^ Руис-Перес, Лидия; Хуан Карлос, Гарсия-Эскартин (2 мая 2017 г.). «Квантовая арифметика с квантовым преобразованием Фурье». Квантовая обработка информации . 16 (6): 152. arXiv : 1411.5949v2 . Бибкод : 2017QuIP...16..152R . дои : 10.1007/s11128-017-1603-1 . S2CID 10948948 .
^ «Суммирующий усилитель представляет собой сумматор напряжения на операционном усилителе» . 22 августа 2013 г.

Дальнейшее чтение [ править ]

Лю, Цо-Кай; Хохулин, Кейт Р.; Шиау, Лих-Эр; Мурога, Сабуро (январь 1974 г.). «Оптимальные однобитные полные сумматоры с различными типами вентилей». Транзакции IEEE на компьютерах . С-23 (1). Лаборатории Белла: IEEE : 63–70. дои : 10.1109/TC.1974.223778 . ISSN 0018-9340 . S2CID 7746693 .
Лай, Хун Чи; Мурога, Сабуро (сентябрь 1979 г.). «Минимальные двоичные параллельные сумматоры с вентилями NOR (NAND)». Транзакции IEEE на компьютерах . С-28 (9). IEEE : 648–659. дои : 10.1109/TC.1979.1675433 . S2CID 23026844 .
Мид, Карвер; Конвей, Линн (1980) [декабрь 1979 г.]. Введение в системы СБИС (1-е изд.). Ридинг, Массачусетс, США: Аддисон-Уэсли . Бибкод : 1980aw...book.....M . ISBN 978-0-20104358-7 . Проверено 12 мая 2018 г.
Давио, Марк; Дешан, Жан-Пьер; Тайзе, Андре (1983). Цифровые системы с реализацией алгоритмов (1-е изд.). Исследовательская лаборатория Philips , Брюссель, Бельгия: John Wiley & Sons , межнаучное издание Wiley. ISBN 978-0-471-10413-1 . LCCN 82-2710 .
Гослинг, Джон (январь 1971 г.). «Обзор методов высокоскоростного сложения». Учеб. ИЭЭ . 188 (1): 29–35. дои : 10.1049/piee.1971.0004 .

Внешние ссылки [ править ]

СМИ, связанные с сумматорами (цифровыми схемами), на Викискладе?
8-битный полный сумматор и вычитатель — демонстрация интерактивного полного сумматора, встроенного в JavaScript исключительно для учебных целей.
Интерактивные демонстрации половинных и полных сумматоров в HTML5
Ширрифф, Кен (ноябрь 2020 г.). «Реверс-инжиниринг схемы упреждающего переноса в процессоре Intel 8008» .

[1] Сингх, Аджай Кумар (2010). Проектирование цифровых СБИС . Прентис Холл Индия. п. 321. ИСБН 9788120341876 – через Google Книги.

[Lancaster_2004-2] Ланкастер, Джеффри А. (2004). Проектирование и разработка программного обеспечения Excel HSC . Паскаль Пресс. п. 180. ИСБН 978-1-74125175-3 .

[Mano_1979-3] Мано, М. Моррис (1979). Цифровая логика и компьютерный дизайн . Прентис-Холл . стр. 119–123 . ISBN 978-0-13-214510-7 .

[4] Теджа, Рави (15 апреля 2021 г.), Схемы половинного и полного сумматора , получено 27 июля 2021 г.

[Fischer-5] Jump up to: Перейти обратно: ^а ^б ^с Фишер, П. «Простые схемные блоки» (PDF) . Гейдельбергский университет. Архивировано из оригинала (PDF) 5 сентября 2021 г. Проверено 05 сентября 2021 г.

[Adder-6] Сатпати, Пинаки (2016). Проектирование и реализация сумматора Carry Select с использованием T-Spice . Якорное академическое издательство. п. 22. ISBN 978-3-96067058-2 .

[Burgess_2011-7] Берджесс, Нил (2011). Быстрые сумматоры с пульсирующим переносом в КМОП СБИС стандартных ячеек . 20-й симпозиум IEEE по компьютерной арифметике . стр. 103–111.

[Brent-Kung_1982-8] Брент, Ричард Пирс ; Кунг, Сян Те (март 1982 г.). «Обычная схема для параллельных сумматоров» . Транзакции IEEE на компьютерах . С-31 (3): 260–264. дои : 10.1109/TC.1982.1675982 . ISSN 0018-9340 . S2CID 17348212 . Архивировано из оригинала 24 сентября 2017 года.

[Kogge-Stone_1973-9] Когге, Питер Майкл ; Стоун, Гарольд С. (август 1973 г.). «Параллельный алгоритм эффективного решения общего класса рекуррентных уравнений». Транзакции IEEE на компьютерах . С-22 (8): 786–793. дои : 10.1109/TC.1973.5009159 . S2CID 206619926 .

[ULVD_2015-10] Рейндерс, Неле; Деэн, Вим (2015). Проектирование энергоэффективных цифровых схем сверхнизкого напряжения . Аналоговые схемы и обработка сигналов (1-е изд.). Чам, Швейцария: Springer International Publishing AG, Швейцария . дои : 10.1007/978-3-319-16136-5 . ISBN 978-3-319-16135-8 . ISSN 1872-082X . LCCN 2015935431 .

[11] Фейнман, Ричард П. (1986). «Квантово-механические компьютеры». Основы физики . 16 (6). Springer Science and Business Media LLC: 507–531. Бибкод : 1986FoPh...16..507F . дои : 10.1007/bf01886518 . ISSN 0015-9018 . S2CID 122076550 .

[12] «Пример кода: квантовый полный сумматор» . QuTech (Технологический университет Делфта (TU Delft) и Нидерландская организация прикладных научных исследований (TNO)).

[13] Дибьенду Чаттерджи, Ариджит Рой (2015). «Схема квантового полусумматора на основе трансмонов» . Успехи теоретической и экспериментальной физики . 2015 (9): 093А02. Бибкод : 2015PTEP.2015i3A02C . дои : 10.1093/ptep/ptv122 .

[14] Дрейпер, Томас Г. (7 августа 2000 г.). «Дополнение о квантовом компьютере». arXiv : Quant-ph/0008033 .

[15] Руис-Перес, Лидия; Хуан Карлос, Гарсия-Эскартин (2 мая 2017 г.). «Квантовая арифметика с квантовым преобразованием Фурье». Квантовая обработка информации . 16 (6): 152. arXiv : 1411.5949v2 . Бибкод : 2017QuIP...16..152R . дои : 10.1007/s11128-017-1603-1 . S2CID 10948948 .

[16] «Суммирующий усилитель представляет собой сумматор напряжения на операционном усилителе» . 22 августа 2013 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]