16-ячеечная сотовая связь

16-ячеечная сотовая связь
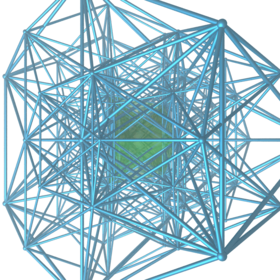Перспективная проекция : первый слой соседних 16-клеточных граней.
Тип	Обычный 4-сотовый Униформа 4-сотовая
Семья	Альтернативные соты гиперкуба
Символ Шлефли	{3,3,4,3}
Диаграммы Кокстера	= =
4-гранный тип	{3,3,4}
Тип ячейки	{3,3}
Тип лица	{3}
Краевая фигура	куб
Вершинная фигура	24-ячеечный
Группа Коксетера	${\tilde {F}}_{4}$ = [3,3,4,3]
Двойной	{3,4,3,3}
Характеристики	вершинно-транзитивный , реберно-транзитивный , грани-транзитивный , клеточно-транзитивный , 4-гранный-транзитивный

В четырехмерной евклидовой геометрии соты из 16 ячеек являются одной из трех регулярных мозаик , заполняющих пространство (или сот ), представленных символом Шлефли {3,3,4,3} и построенных с помощью 4-мерной упаковки 16-клеточные грани , по три вокруг каждой грани.

Его двойником являются соты из 24 ячеек . Его вершинная фигура представляет собой 24-клеточную фигуру . Расположение вершин называется _{B 4} , D ₄ или F ₄ решеткой . ^[1]^[2]

Альтернативные названия

Гексадекахорные тетрасоты/соты
Демитессерактические тетрасоты / соты

Координаты

Вершины можно размещать во всех целочисленных координатах (i,j,k,l), чтобы сумма координат была четной.

Д ₄Решетка

Вершинное расположение сот из 16 ячеек называется D ₄ решеткой или решеткой F ₄ . ^[2] Вершины этой решетки являются центрами 3-сфер в самой плотной известной упаковке равных сфер в 4-пространстве; ^[3] его число поцелуев — 24, что также совпадает с числом поцелуев в R. ⁴, как доказал Олег Мусин в 2003 году. ^[4]^[5]

Соответствующий Д ⁺
₄ решетка (также называемая D ²
₄ ) может быть построена объединением двух решеток D ₄ и идентична решетке C ₄ : ^[6]

∪

=

Поцелуйный номер для D ⁺
₄ это 2 ³ = 8, (2 ^{п – 1} для n < 8, 240 для n = 8 и 2 n ( n – 1) для n > 8). ^[7]

Соответствующий Д ^*
₄ решетка (также называемая D ⁴
₄ и С ²
₄ ) может быть построена объединением всех четырех решеток D ₄ , но она идентична D ₄ решетке : это также 4-мерная объемноцентрированная куба , объединение двух 4-кубических сот в двойных положениях. ^[8]

∪

=

∪

.

Поцелуйное число D ^*
₄Решетка _{(и решетка D 4} ) равна 24 ^[9] а его мозаика Вороного представляет собой соты из 24 ячеек , , содержащий все выпрямленные 16-ячеечные ( 24-клеточные ) ячейки Вороного , или . ^[10]

Симметричные конструкции

Есть три различные конструкции симметрии этой мозаики. Каждая симметрия может быть представлена различным расположением цветных 16-клеточных граней.

Группа Коксетера	Символ Шлефли	Диаграмма Кокстера	Вершинная фигура Симметрия	Фасеты /краска
${\tilde {F}}_{4}$ = [3,3,4,3]	{3,3,4,3}		[3,4,3], порядок 1152	24: 16-ячеечный
${\tilde {B}}_{4}$ = [3 ^1,1,3,4]	= ч{4,3,3,4}	=	[3,3,4], порядок 384	16+8: 16-ячеечный
${\tilde {D}}_{4}$ = [3 ^1,1,1,1]	{3,3 ^1,1,1} = ч{4,3,3 ^1,1}	=	[3 ^1,1,1], заказ 192	8+8+8: 16 ячеек
2×½ ${\tilde {C}}_{4}$ = [[(4,3,3,4,2 ⁺)]]	хт _0.4 {4,3,3,4}			8+4+4: 4-полукуб 8: 16-ячеечный

Связанные соты

Он связан с правильными гиперболическими 5-мерными 5-ортоплексными сотами {3,3,3,4,3} с 5-ортоплексными гранями, правильным 4-мерным многогранником с 24 ячейками {3,4,3} с октаэдрическая (3-ортоплекс) ячейка и куб {4,3} с квадратными гранями (2-ортоплекс).

У него есть двумерный аналог {3,6} , и как альтернативная форма ( демитессерактические соты , h{4,3,3,4}) он связан с чередующимися кубическими сотами .

Эта сота — одна из 20 однородных сот, построенных ${\tilde {D}}_{5}$ Группа Кокстера , все, кроме трех, повторяются в других семействах благодаря расширенной симметрии, что видно по графической симметрии колец в диаграммах Кокстера – Дынкина . 20 перестановок перечислены с наивысшим расширенным отношением симметрии:

Соты D5
Extended symmetry	Extended diagram	Extended group	Honeycombs
[3^1,1,3,3^1,1]		${\tilde {D}}_{5}$
<[3^1,1,3,3^1,1]> ↔ [3^1,1,3,3,4]	↔	${\tilde {D}}_{5}$ ×2₁ = ${\tilde {B}}_{5}$	, , , , , ,
[[3^1,1,3,3^1,1]]		${\tilde {D}}_{5}$ ×2₂	,
<2[3^1,1,3,3^1,1]> ↔ [4,3,3,3,4]	↔	${\tilde {D}}_{5}$ ×4₁ = ${\tilde {C}}_{5}$	, , , , ,
[<2[3^1,1,3,3^1,1]>] ↔ [[4,3,3,3,4]]	↔	${\tilde {D}}_{5}$ ×8 = ${\tilde {C}}_{5}$ ×2	, ,

См. также

Правильные и однородные соты в 4-мерном пространстве:

Примечания

^ «Решетка F4» .
^ Перейти обратно: ^а ^б «Решетка Д4» .
^ Конвей и Слоан, Сферические упаковки, решетки и группы , 1.4 n-мерные упаковки, стр.9
^ Конвей и Слоан, Упаковки сфер, решетки и группы , 1.5 Краткое изложение результатов задачи упаковки сфер, стр. 12
^ О. Р. Мусин (2003). «Проблема двадцати пяти сфер». Расс. Математика. Сурв . 58 (4): 794–795. Бибкод : 2003РуМаС..58..794М . дои : 10.1070/RM2003v058n04ABEH000651 .
^ Конвей и Слоан, Сферические упаковки, решетки и группы , 7.3 Упаковка D ₃⁺, стр.119
^ Конвей и Слоан, Сферические упаковки, решетки и группы , с. 119
^ Конвей и Слоан, Сферические упаковки, решетки и группы , 7.4 Двойственная решетка D ₃^*, стр.120
^ Конвей и Слоан, Сферические упаковки, решетки и группы , с. 120
^ Конвей и Слоан, Сферические упаковки, решетки и группы , с. 466

Ссылки

Коксетер, Правильные многогранники HSM (3-е издание, 1973 г.), Дуврское издание, ISBN 0-486-61480-8
- стр. 154–156: Частичное усечение или чередование, представленное префиксом h : h{4,4} = {4,4}; ч{4,3,4} = {3 ^1,1,4}, ч{4,3,3,4} = {3,3,4,3}, ...
Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
Георгий Ольшевский, Равномерные паноплоидные тетракомбы , Рукопись (2006) (Полный список из 11 выпуклых однородных мозаик, 28 выпуклых однородных сот и 143 выпуклых однородных тетракомб)
Клитцинг, Ричард. «4D евклидовы мозаики» . x3o3o4o3o - шестнадцатеричный - O104
Конвей Дж. Х., Слоан Н. Дж. Х. (1998). Сферические упаковки, решетки и группы (3-е изд.). ISBN 0-387-98585-9 .

v т и Основные выпуклые правильные и однородные соты размеров 2–9.
Космос	Семья	${\tilde {A}}_{n-1}$	${\tilde {C}}_{n-1}$	${\tilde {B}}_{n-1}$	${\tilde {D}}_{n-1}$	${\tilde {G}}_{2}$ / ${\tilde {F}}_{4}$ / ${\tilde {E}}_{n-1}$
И ²	Равномерная укладка плитки	{3 ^[3]}	д ₃	HD ₃	квартал ₃	Шестиугольный
И ³	Равномерные выпуклые соты	{3 ^[4]}	д ₄	HD ₄	4 _{квартала}
И ⁴	Униформа 4-сотовая	{3 ^[5]}	д ₅	hδ ₅	qδ ₅	24-ячеистые соты
И ⁵	Униформа 5-сотовая	{3 ^[6]}	д ₆	HD ₆	qδ ₆
И ⁶	Униформа 6-сотовая	{3 ^[7]}	д ₇	hδ ₇	qδ ₇	2 ₂₂
И ⁷	Униформа 7-сотовая	{3 ^[8]}	д ₈	hδ ₈	8 _{кварталов}	1 ₃₃ • 3 ₃₁
И ⁸	Униформа 8-сотовая	{3 ^[9]}	д ₉	HD ₉	qδ ₉	1 ₅₂ • 2 ₅₁ • 5 ₂₁
И ⁹	Униформа 9-сотовая	{3 ^[10]}	д ₁₀	HD ₁₀	10 _{кварталов}
И ¹⁰	Униформа 10-сотовая	{3 ^[11]}	д ₁₁	HD ₁₁	qδ ₁₁
И ^{п -1}	Равномерный ( n -1)- сотовый	{3 ^[н]}	δ _н	hδ _н	qδ _н	1 _{лиц 2} • 2 _{лиц 1} • лиц ₂₁

[1] «Решетка F4» .

[www2.research.att.com-2] Перейти обратно: ^а ^б «Решетка Д4» .

[3] Конвей и Слоан, Сферические упаковки, решетки и группы , 1.4 n-мерные упаковки, стр.9

[4] Конвей и Слоан, Упаковки сфер, решетки и группы , 1.5 Краткое изложение результатов задачи упаковки сфер, стр. 12

[Musin-5] О. Р. Мусин (2003). «Проблема двадцати пяти сфер». Расс. Математика. Сурв . 58 (4): 794–795. Бибкод : 2003РуМаС..58..794М . дои : 10.1070/RM2003v058n04ABEH000651 .

[6] Конвей и Слоан, Сферические упаковки, решетки и группы , 7.3 Упаковка D ₃⁺, стр.119

[7] Конвей и Слоан, Сферические упаковки, решетки и группы , с. 119

[8] Конвей и Слоан, Сферические упаковки, решетки и группы , 7.4 Двойственная решетка D ₃^*, стр.120

[9] Конвей и Слоан, Сферические упаковки, решетки и группы , с. 120

[10] Конвей и Слоан, Сферические упаковки, решетки и группы , с. 466

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]