Введение в электромагнетизм

Эта статья о концептуальном понимании темы. Более подробное математическое рассмотрение см. в разделе «Электромагнетизм» .

Электромагнетизм – одна из фундаментальных сил природы. Вначале электричество и магнетизм изучались отдельно и рассматривались как отдельные явления. Ганс Христиан Эрстед обнаружил, что эти два явления связаны между собой: электрические токи порождают магнетизм. Майкл Фарадей обнаружил обратное: магнетизм может вызывать электрические токи, а Джеймс Клерк Максвелл объединил все это в единую теорию электромагнетизма . Уравнения Максвелла также указывали на существование электромагнитных волн , а эксперименты Генриха Герца подтвердили это, сделав радио возможным . Максвелл также правильно постулировал, что свет представляет собой форму электромагнитной волны, что сделало всю оптику отраслью электромагнетизма. Радиоволны отличаются от света только тем, что длина волны первых значительно больше, чем у вторых. Альберт Эйнштейн показал, что магнитное поле возникает в результате релятивистского движения электрического поля и, следовательно, магнетизм — это всего лишь побочный эффект электричества. Современная теоретическая трактовка электромагнетизма представляет собой квантовое поле в квантовой электродинамике .

Во многих ситуациях, представляющих интерес для электротехники , нет необходимости применять квантовую теорию для получения правильных результатов. Классическая физика по-прежнему является точным приближением в большинстве ситуаций, связанных с макроскопическими объектами. За некоторыми исключениями, квантовая теория необходима только на атомном уровне , и можно применить более простую классическую трактовку. Дальнейшие упрощения лечения возможны в ограниченных ситуациях. Электростатика имеет дело только со стационарными электрическими зарядами , поэтому магнитные поля не возникают и не рассматриваются. Постоянные магниты можно описать безотносительно к электричеству или электромагнетизму. Теория цепей имеет дело с электрическими сетями , в которых поля в основном сосредоточены вокруг проводников с током . В таких схемах можно обойтись даже без уравнений Максвелла и использовать более простые формулировки. С другой стороны, квантовая трактовка электромагнетизма важна в химии . Химические реакции и химическая связь являются результатом квантово-механических процессов. взаимодействие электронов вокруг атомов . Квантовые соображения также необходимы для объяснения поведения многих электронных устройств, например туннельного диода .

Электрический заряд

Закон Кулона говорит нам, что одноименные заряды отталкиваются, а противоположные заряды притягиваются.

Электромагнетизм является одной из фундаментальных сил природы наряду с гравитацией , сильным и слабым взаимодействием . В то время как гравитация действует на все вещи, имеющие массу , электромагнетизм действует на все вещи, имеющие электрический заряд . Более того, поскольку существует закон сохранения массы, согласно которому масса не может быть создана или уничтожена, существует также сохранение заряда , что означает, что заряд в закрытой системе (где заряды не покидают и не входят) должен оставаться постоянным. Фундаментальным законом, описывающим силу гравитации, действующую на массивный объект в классической физике, является закон гравитации Ньютона . Аналогично, закон Кулона — это фундаментальный закон, описывающий силу, с которой заряженные объекты действуют друг на друга. Оно определяется формулой

$F=k_{\text{e}}{q_{1}q_{2} \over r^{2}}$

где F — сила, k _e — постоянная Кулона , q ₁ и q ₂ — величины двух зарядов, а r ² есть квадрат расстояния между ними. Оно описывает тот факт, что одноименные заряды отталкивают друг друга, тогда как противоположные заряды притягивают друг друга, и что чем сильнее заряды частиц, тем сильнее сила, которую они оказывают друг на друга. Этот закон также представляет собой закон обратных квадратов , который означает, что при увеличении расстояния между двумя частицами сила, действующая на них, уменьшается в четыре раза.

Электрические и магнитные поля

Линии электрического поля направлены от положительных зарядов к отрицательным.

Сила, действующая на положительный заряд электрическим полем (слева) и магнитным полем (справа), в совокупности дает силу Лоренца .

В физике поля — это объекты, которые взаимодействуют с материей и могут быть описаны математически, присвоив значение каждой точке пространства и времени. Векторные поля — это поля, которым присвоено как числовое значение, так и направление в каждой точке пространства и времени. Электрические заряды создают векторное поле, называемое электрическим полем . Числовое значение электрического поля, также называемое напряженностью электрического поля, определяет силу электрической силы, которую заряженная частица будет чувствовать в поле, а направление поля определяет, в каком направлении будет действовать сила. направление электрического поля совпадает с направлением силы, действующей на положительные заряды, и противоположно направлению силы, действующей на отрицательные заряды. Поскольку положительные заряды отталкиваются другими положительными зарядами и притягиваются к отрицательным зарядам, это означает, что электрические поля направлены от положительных зарядов к отрицательным зарядам. Эти свойства электрического поля заключены в уравнении электрической силы, действующей на заряд, записанной через электрическое поле: $$F=qE$$где F — сила, действующая на заряд в электрическом поле E. q

Помимо создания электрического поля, заряженные частицы будут создавать магнитное поле , когда они находятся в состоянии движения, которое будет ощущаться другими зарядами, находящимися в движении (а также постоянными магнитами ). Направление силы, действующей на движущийся заряд со стороны магнитного поля, перпендикулярно как направлению движения, так и направлению силовых линий магнитного поля и может быть найдено по правилу правой руки . Сила силы определяется уравнением $$F=qvB\sin \theta$$где F — сила, действующая на заряд q со скоростью v в магнитном поле B , направленном в направлении угла θ от направления движения заряда.

Если нет заряда, окруженного замкнутой поверхностью, то количество электрического поля, втекающего в нее, должно в точности компенсироваться электрическим полем, вытекающим из нее.

Поскольку поток магнитного поля из замкнутой поверхности должен компенсироваться потоком в нее, магниты должны иметь как северный, так и южный полюса, которые нельзя разделить на монополи.

Сочетание электрических и магнитных сил, действующих на заряженную частицу, называется силой Лоренца . Классический электромагнетизм полностью описывается силой Лоренца вместе с набором уравнений, называемых уравнениями Максвелла . Первое из этих уравнений известно как закон Гаусса . Он описывает электрическое поле, создаваемое заряженными частицами и распределением зарядов . Согласно закону Гаусса, поток (или поток) электрического поля через любую замкнутую поверхность пропорционален количеству заряда, заключенного в этой поверхности. Это означает, что чем больше заряд, тем больше создаваемое электрическое поле. Это также имеет и другие важные последствия. Например, этот закон означает, что если нет заряда, окруженного поверхностью, то либо электрическое поле отсутствует вообще, либо, если заряд есть вблизи замкнутой поверхности, но за ее пределами, поток электрического поля в поверхность должна в точности компенсироваться с истечением с поверхности. Второе из уравнений Максвелла известно как закон Гаусса для магнетизма и, как и первый закон Гаусса, описывает поток, но вместо электрического потока он описывает магнитный поток . Согласно закону магнетизма Гаусса поток магнитного поля через замкнутую поверхность всегда равен нулю. Это означает, что при наличии магнитного поля поток в замкнутую поверхность всегда будет компенсироваться потоком из замкнутой поверхности. Этот закон также называют «отсутствием магнитных монополей», поскольку он означает, что любой магнитный поток, вытекающий из замкнутой поверхности, должен течь обратно в нее, а это означает, что положительные и отрицательные магнитные полюса должны собраться вместе в магнитный диполь и никогда не могут быть разделены на две части. магнитные монополи . В этом отличие от электрических зарядов, которые могут существовать как отдельные положительные и отрицательные заряды.

Правило правого хвата для прямой проволоки (слева) и спиральной проволоки (справа). Электрический ток, проходящий через провод, намотанный на железный сердечник, может создать электромагнит .

Третье из уравнений Максвелла называется законом Ампера-Максвелла . Он утверждает, что магнитное поле может быть создано электрическим током . Направление магнитного поля определяется правилом правой руки Ампера . Если провод прямой, то магнитное поле обвивается вокруг него, как сомкнутые пальцы в правиле правой руки. Если провод смотан в катушки, то магнитное поле внутри катушек направлено по прямой линии, как вытянутый большой палец в правиле правого хвата. Когда электрический ток используется для создания магнита таким образом, его называют электромагнитом . В электромагнитах часто используется провод, скрученный в соленоид вокруг железного сердечника, который усиливает магнитное поле, создаваемое из-за намагничивания железного сердечника. Расширение закона Максвеллом гласит, что изменяющееся во времени электрическое поле также может генерировать магнитное поле. Точно так же закон индукции Фарадея утверждает, что магнитное поле может производить электрический ток. Например, магнит, вдвигаемый и вынимаемый из катушки с проводами, может создавать в катушках электрический ток, пропорциональный силе магнита, а также количеству витков и скорости, с которой магнит вставляется и извлекается из катушки. катушки. Этот принцип важен для трансформаторов , которые используются для преобразования токов высокого напряжения в низкое и наоборот. Они необходимы для преобразования электроэнергии из сети высокого напряжения в электричество низкого напряжения, которое можно безопасно использовать в домах. Формулировка закона Максвеллом представлена ​​в уравнении Максвелла-Фарадея — четвертом и последнем из уравнений Максвелла, — которое гласит, что изменяющееся во времени магнитное поле создает электрическое поле.

Электромагнитный спектр

Вместе уравнения Максвелла составляют единую единую теорию электрического и магнитного полей, и работу Максвелла по созданию этой теории назвали «вторым великим объединением в физике» после первого великого объединения закона всемирного тяготения Ньютона . Решение уравнений Максвелла в свободном пространстве (где нет зарядов и токов) приводит к волновым уравнениям, соответствующим электромагнитным волнам (как с электрическими, так и с магнитными компонентами), движущимся со скоростью света . Наблюдение того, что эти волновые решения имеют скорость волны, точно равную скорости света, привело Максвелла к гипотезе, что свет является формой электромагнитного излучения, и к предположению, что может существовать другое электромагнитное излучение с другими длинами волн. Существование электромагнитного излучения было доказано Генрихом Герцем в серии экспериментов с 1886 по 1889 год, в которых он обнаружил существование радиоволн . Полный электромагнитный спектр (в порядке возрастания частоты) состоит из радиоволн, микроволн , инфракрасного излучения , видимого света , ультрафиолетового света , рентгеновских лучей и гамма-лучей .

Лабораторный каркас

Система покоя электрона

Дальнейшее объединение электромагнетизма произошло со специальной теорией относительности Эйнштейна . Согласно специальной теории относительности, наблюдатели, движущиеся с разной скоростью относительно друг друга, занимают разные системы отсчета . Если один наблюдатель движется относительно другого наблюдателя, то он испытывает сокращение длины , когда неподвижные объекты кажутся движущемуся наблюдателю ближе друг к другу, чем наблюдателю в состоянии покоя. Следовательно, если электрон движется с той же скоростью, что и ток в нейтральном проводе, то они воспринимают текущие электроны в проводе как неподвижные относительно него, а положительные заряды - как сжатые вместе. В лабораторных условиях электрон движется и поэтому ощущает магнитную силу тока в проводе, но поскольку провод нейтрален, он не ощущает электрической силы. электрона Но в системе покоя положительные заряды кажутся ближе друг к другу по сравнению с текущими электронами, и поэтому провод кажется положительно заряженным. Следовательно, в системе покоя электрона он не ощущает магнитной силы (поскольку он не движется в своей собственной системе отсчёта), но ощущает электрическую силу, возникающую из-за положительно заряженного провода. Этот результат теории относительности доказывает, что магнитные поля — это просто электрические поля в другой системе отсчета (и наоборот), и поэтому они являются разными проявлениями одного и того же основного поля. электромагнитное поле .

Проводники, изоляторы и цепи

Дирижеры

Заряды в идеальном проводнике перестраиваются так, что электрическое поле внутри всегда равно нулю.

Проводник – это материал, который позволяет электронам легко течь. Наиболее эффективными проводниками обычно являются металлы , поскольку их довольно точно можно описать моделью свободных электронов , в которой электроны делокализуются из атомных ядер , оставляя положительные ионы окруженными облаком свободных электронов. Примеры хороших проводников включают медь , алюминий и серебро . Провода в электронике часто изготавливаются из меди.

Основными свойствами проводников являются:

1. Электрическое поле внутри идеального проводника равно нулю. Поскольку заряды могут свободно перемещаться в проводнике, когда на них воздействует внешнее электрическое поле, они перестраиваются так, что поле, создаваемое их конфигурацией, в точности нейтрализует внешнее электрическое поле внутри проводника.
2. Электрический потенциал везде одинаков внутри проводника и постоянен по всей поверхности проводника. Это следует из первого утверждения, поскольку поле внутри проводника везде равно нулю и, следовательно, потенциал постоянен и внутри проводника.
3. Электрическое поле перпендикулярно поверхности проводника. Если бы это было не так, поле имело бы ненулевой компонент на поверхности проводника, что заставляло бы заряды в проводнике перемещаться до тех пор, пока этот компонент поля не стал бы равен нулю.
4. Чистый электрический поток через поверхность пропорционален заряду, заключенному в поверхности. Это повторение закона Гаусса .

В некоторых материалах электроны связаны с атомными ядрами и поэтому не могут свободно перемещаться, но энергия, необходимая для их освобождения, невелика. В этих материалах, называемых полупроводниками , проводимость низкая при низких температурах, но при повышении температуры электроны получают больше тепловой энергии , и проводимость увеличивается. Кремний является примером полупроводников, которые можно использовать для создания солнечных элементов , которые становятся тем более проводящими, чем больше энергии они получают от фотонов Солнца.

Сверхпроводники — это материалы, которые практически не оказывают сопротивления потоку электронов при охлаждении ниже определенной критической температуры. Сверхпроводимость можно объяснить только квантовомеханическим принципом Паули, который гласит, что никакие два фермиона (электрон — это разновидность фермиона) не могут занимать одно и то же квантовое состояние . В сверхпроводниках ниже определенной температуры электроны образуют связанные пары бозонов , которые не следуют этому принципу, а это означает, что все электроны могут попасть на один и тот же энергетический уровень и двигаться вместе равномерно в токе.

Изоляторы

В диэлектрическом материале электрическое поле может поляризовать материал.

Изоляторы представляют собой материалы, обладающие высоким сопротивлением потоку электронов, поэтому их часто используют для покрытия проводящих проводов в целях безопасности. В изоляторах электроны прочно связаны с атомными ядрами, и энергия, необходимая для их освобождения, очень высока, поэтому они не могут свободно двигаться и сопротивляются движению, вызванному внешним электрическим полем. Однако некоторые изоляторы, называемые диэлектриками , могут поляризоваться под воздействием внешнего электрического поля, так что заряды мгновенно смещаются, образуя диполи , которые создают положительную и отрицательную стороны. Диэлектрики используются в конденсаторах, чтобы позволить им хранить больше электрической потенциальной энергии в электрическом поле между пластинами конденсатора.

Конденсаторы

Конденсатор с параллельными пластинами

Конденсатор — это электронный компонент , который сохраняет электрическую потенциальную энергию в электрическом поле между двумя противоположно заряженными проводящими пластинами. Если одна из проводящих пластин имеет плотность заряда + Q/A , а другая - - Q/A , где A - площадь пластин, то между ними возникнет электрическое поле. Разность потенциалов между двумя параллельными пластинами V можно определить математически как

$V={Qd \over \varepsilon _{0}A}$

где d - расстояние между пластинами и ${\textstyle \varepsilon _{0}}$ - диэлектрическая проницаемость свободного пространства . Способность конденсатора сохранять электрическую потенциальную энергию измеряется емкостью, которая определяется как ${\textstyle C=Q/V}$ а для конденсатора с параллельными пластинами это

$C={\varepsilon _{0}A \over d}$

Если между пластинами поместить диэлектрик, то диэлектрическая проницаемость свободного пространства умножается на проницаемость и емкость увеличивается. относительную диэлектрическую Максимальная энергия, которую может сохранить конденсатор, пропорциональна емкости и квадрату разности потенциалов между обкладками.

$E={\frac {1}{2}}CV^{2}$

Индукторы

Индуктор — это электронный компонент, который сохраняет энергию в магнитном поле внутри катушки с проводом. Проволочная катушка с током индуцирует магнитное поле в соответствии с законом цепи Ампера . Чем больше ток I , тем больше энергия, запасенная в магнитном поле, и тем меньше индуктивность , которая определяется ${\textstyle L=\Phi _{B}/I}$ где ${\textstyle \Phi _{B}}$ — магнитный поток, создаваемый катушкой с проводом. Индуктивность является мерой сопротивления цепи изменению тока, поэтому катушки индуктивности с высокой индуктивностью также можно использовать для противодействия переменному току .

Другие компоненты схемы

Компонент	Основная функция	Схематическое обозначение
Резистор	Препятствует прохождению тока
Батарея	Действует как источник питания
Источник постоянного напряжения	Действует как источник постоянного тока (DC), постоянного тока, направленного в одном направлении.
Источник переменного напряжения	Действует как источник переменного тока (AC), переменного тока, который периодически меняет направление.
Диод	Позволяет току легко течь в одном направлении, но не в другом.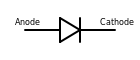
Конденсатор	Сохраняет энергию в электрических полях, сохраняет заряд, пропускает переменный ток низкой частоты.
Индуктор	Хранит энергию в магнитных полях, сопротивляется изменению тока

Окружные законы

Правило соединения Кирхгофа (вверху):

Я ₁ + Я ₂ + Я ₃ = Я ₄ + Я ₅

Правило петли Кирхгофа (ниже):

В ₁ + В ₂ + В ₃ + В ₄ = 0

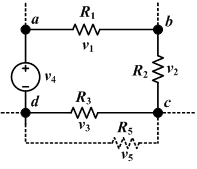
Теория цепей имеет дело с электрическими сетями , в которых поля в основном сосредоточены вокруг проводников с током . В таких цепях можно использовать простые законы цепей вместо того, чтобы выводить все поведение цепей непосредственно из электромагнитных законов. Закон Ома устанавливает связь между током I и напряжением V цепи, вводя величину, известную как сопротивление R.

Закон Ома: $I=V/R$

Мощность определяется как $P=IV$ поэтому закон Ома можно использовать, чтобы определить мощность цепи в терминах других величин.

$P=IV=V^{2}/R=I^{2}R$

Правило соединения Кирхгофа гласит, что ток, входящий в соединение (или узел), должен быть равен току, выходящему из узла. Это происходит из-за сохранения заряда , поскольку ток определяется как поток заряда с течением времени. Если ток разделяется при выходе из соединения, сумма результирующих разделенных токов равна входящей в цепь.

Правило петли Кирхгофа гласит, что сумма напряжений в замкнутом контуре вокруг цепи равна нулю. Это происходит из-за того, что электрическое поле консервативно , а это означает, что независимо от выбранного пути потенциал в точке не изменится, когда вы вернетесь туда.

Правила также могут подсказать нам, как складывать такие величины, как ток и напряжение в последовательных и параллельных цепях .

В последовательных цепях ток остается одинаковым для каждого компонента, а напряжения и сопротивления складываются:

$V_{tot}=V_{1}+V_{2}+V_{3}+\ldots \qquad R_{tot}=R_{1}+R_{2}+R_{3}+\ldots \qquad I=I_{1}=I_{2}=I_{3}=\ldots$

Для параллельных цепей напряжение остается одинаковым для каждого компонента, а токи и сопротивления связаны, как показано:

$V_{tot}=V_{1}=V_{2}=V_{3}=\ldots \qquad {1 \over R_{tot}}={1 \over R_{1}}+{1 \over R_{2}}+{1 \over R_{3}}+\ldots \qquad I_{tot}=I_{1}+I_{2}+I_{3}+\ldots$

См. также

• Список учебников по электромагнетизму