Д 6 Многогранник
Эта статья включает список литературы , связанную литературу или внешние ссылки , но ее источники остаются неясными, поскольку в ней отсутствуют встроенные цитаты . ( февраль 2023 г. ) |
 6-демикуб |  6-ортоплекс |
В 6-мерной геометрии существует 47 однородных многогранников с симметрией D6 , из которых 16 уникальных и 31 общий с симметрией B6 . Существуют две правильные формы: 6-ортоплекс и 6-демикуб с 12 и 32 вершинами соответственно.
Их можно визуализировать как симметричные ортогональные проекции в плоскостях Кокстера группы D 6 Кокстера и других подгрупп.
Графики
[ редактировать ]Симметричные ортогональные проекции этих 16 многогранников можно построить в плоскостях D 6 , D 5 , D 4 , D 3 , A 5 , A 3 , Кокстера . AK k имеет симметрию [k+1] , D ] имеет симметрию [2(k-1) . B 6 также включен, хотя в этих многогранниках существует только половина его симметрии [12].
Каждый из этих 16 многогранников показан в этих 7 плоскостях симметрии, с нарисованными вершинами и ребрами, а вершины окрашены в соответствии с количеством перекрывающихся вершин в каждой проективной позиции.
| # | Кокстера Плоские графы | Диаграмма Кокстера Имена | ||||||
|---|---|---|---|---|---|---|---|---|
| Б 6 [12/2] | Д 6 [10] | Д 5 [8] | Д 4 [6] | Д 3 [4] | AА5 [6] | AА3 [4] | ||
| 1 |  |  | 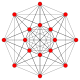 | 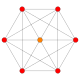 | 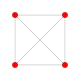 | 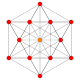 | 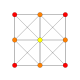 | 6-демикуб Гемигексеракт (хакс) |
| 2 |  |  |  |  |  |  |  | кантик 6-куб Усеченный полугексеракт (такс) |
| 3 |  |  |  |  |  |  |  | рунчич 6-куб. Малый ромбовидный полугексеракт (сиракс) |
| 4 |  |  |  |  |  |  |  | стерический 6-куб Малый призматический гемигексеракт (софакс) |
| 5 |  |  |  |  |  |  |  | пентик 6-кубовый Мелкоклеточный полугексеракт (сохакс) |
| 6 |  |  |  |  |  |  |  | рунцикантический 6-кубовый Большой ромбовидный полугексеракт (гирхакс) |
| 7 |  |  |  |  |  |  |  | стерикантический 6-кубовый Призматоусеченный гемигексеракт (питакс) |
| 8 |  |  |  |  |  |  |  | стерирунный 6-куб. Призматоромбовидный полугексеракт (прогакс) |
| 9 |  |  |  |  |  |  |  | Стерикантический 6-кубовый Целлитусеченный гемигексеракт (катикс) |
| 10 |  |  |  |  |  |  |  | Пентирунчик 6-кубовый Целлиромбовидный гемигексеракт (крохакс) |
| 11 |  |  |  |  |  |  |  | Пентистерик 6-кубовый Целлипризматический гемигексеракт (кофикс) |
| 12 |  |  |  |  |  |  |  | Стерилизатор 6-кубовый Большой призматический гемигексеракт (гофакс) |
| 13 |  |  |  |  |  |  |  | Пентирунсикантик 6-кубовый Целлигреатор ромбовидный полугексеракт (кагрохакс) |
| 14 |  |  |  |  |  |  |  | Пентистерикантический 6-куб. Целлипизматоусеченный гемигексеракт (каптикс) |
| 15 |  |  |  |  |  |  |  | Пентистерирунковый 6-куб. Целлипризматор ромбовидный полугексеракт (капрогакс) |
| 16 |  | 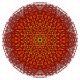 |  |  |  |  |  | Пентистерирунцикантический 6-кубовый Большой клеточный гемигексеракт (гочакс) |
Ссылки
[ редактировать ]- ХСМ Коксетер :
- HSM Coxeter, Правильные многогранники , 3-е издание, Дувр, Нью-Йорк, 1973 г.
- Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380-407, МР 2,10]
- (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559-591]
- (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
- Н. В. Джонсон : Теория однородных многогранников и сот , доктор философии. Диссертация, Университет Торонто, 1966 г.
- Клитцинг, Ричард. «6D однородные многогранники (полипеты)» .