Удлиненный купол

Набор удлиненных куполов
Пример пятиугольной формы
Лица	n треугольников 3n квадратов 1 н-гон 1 2n-угольник
Края	9н
Вершины	5н
Группа симметрии	C nv , [n], (*nn)
Ротационная группа	С н , [н] + , (нн)
Двойной многогранник
Характеристики	выпуклый

В геометрии представляют вытянутые купола собой бесконечное множество многогранников, построенных путем присоединения n-угольного купола к 2n-угольной призме .

Есть три удлиненных купола , которые представляют собой тела Джонсона , состоящие из правильных треугольников, квадратов и пятиугольников. Высшие формы можно построить с помощью равнобедренных треугольников. Присоединение треугольной призмы к кубу также образует многогранник, но имеет две пары копланарных граней, поэтому не является телом Джонсона. Высшие формы могут быть построены без правильных граней.

Формы

	имя	лица
	удлиненный двуугольный купол	2 треугольника, 6+1 квадрата
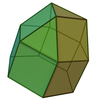	удлиненный треугольный купол ( J18 )	3+1 треугольников, 9 квадратов, 1 шестиугольник
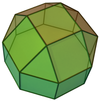	удлиненный квадратный купол ( J19 )	4 треугольника, 12+1 квадрат, 1 восьмиугольник
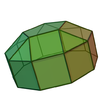	удлиненный пятиугольный купол ( J20 )	5 треугольников, 15 квадратов, 1 пятиугольник, 1 десятиугольник.
	удлиненный шестиугольный купол	6 треугольников, 18 квадратов, 1 шестиугольник, 1 двенадцатиугольник.

См. также

• Гироудлиненный бикупола

Ссылки

• Норман В. Джонсон , «Выпуклые тела с правильными гранями», Canadian Journal of Mathematics, 18 , 1966, страницы 169–200. Содержит исходное перечисление 92 тел и гипотезу об отсутствии других.
• Виктор А. Залгаллер (1969). Выпуклые многогранники с правильными гранями . Консультантское бюро. Нет ISBN. Первое доказательство того, что тел Джонсона всего 92.