Усеченный трапецоэдр

Набор n -угольных усеченных трапецоэдров
Пример: пятиугольный усеченный трапецоэдр ( правильный додекаэдр )
Лица	2 n -сторонних многоугольника , 2 n пятиугольников
Края	6 н
Вершины	4 n
Обозначение Конвея	t4dA4 t5dA5 t6dA6
Группа симметрии	Д н д , [2 + ,2 n ], (2* n ), порядка 4 n
Группа вращения	Д н , [2,n] + , (22 n ), порядок 2 n
Двойной многогранник	гироудлиненные бипирамиды
Характеристики	выпуклый

В геометрии n - угольный усеченный трапецоэдр — это многогранник, образованный n -угольным трапецоэдром с n -угольными пирамидами , усеченными его полярной оси из двух вершин .

Вершины существуют в виде 4 n- угольников в четырех параллельных плоскостях с переменной ориентацией в середине, образующей пятиугольники .

Правильный додекаэдр — наиболее распространенный многогранник этого класса, являющийся платоновым телом с 12 конгруэнтными пятиугольными гранями.

Усеченный трапецоэдр имеет все вершины с тремя гранями. Это означает, что двойственные многогранники , набор гировытянутых дипирамид , имеют все треугольные грани. Например, икосаэдр является двойником додекаэдра .

Формы

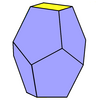
• Треугольный усеченный трапецоэдр ( тело Дюрера ) – 6 пятиугольников, 2 треугольника, двойная гировытянутая треугольная дипирамида.
• Усеченно-квадратный трапецоэдр – 8 пятиугольников, 2 квадрата, двойная гировытянутая квадратная дипирамида.
• Усеченный пятиугольный трапецоэдр или правильный додекаэдр - 12 пятиугольных граней, двойной икосаэдр.
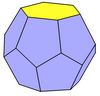
• Усеченный шестиугольный трапецоэдр – 12 пятиугольников, 2 шестиугольника, двойная гировытянутая шестиугольная дипирамида.
• ...
• Усеченный n -угольный трапецоэдр – 2 n пятиугольников, 2 n- угольника, двойные гировытянутые дипирамиды.

См. также

• Уменьшенный трапецоэдр

Внешние ссылки

• Обозначение Конвея для многогранников. Попробуйте: «t n dA n », где n = 4,5,6... пример «t5dA5» — додекаэдр.