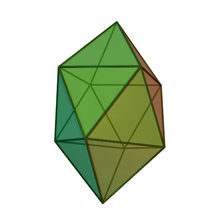
Гироудлиненная квадратная бипирамида

Гироудлиненная квадратная бипирамида
Тип	Гироудлиненная бипирамида , Дельтаэдр , Джонсон 16 ​ – 17 ​ – 18 ​
Лица	16 треугольников
Края	24
Вершины	10
Конфигурация вершин	$2\times (3^{4})+8\times (3^{5})$
Группа симметрии	$D_{4d}$
Двойной многогранник	Усеченный квадратный трапецоэдр
Характеристики	выпуклый
Сеть

В геометрии гировытянутая квадратная бипирамида представляет собой многогранник с 16 треугольными гранями. ее можно построить из квадратной антипризмы , прикрепив две равносторонние квадратные пирамиды к каждой ее квадратной грани . Эту же форму еще называют гексакаидекадельтаэдр. , гекадекадельтаэдр , или квадратная антипризма тетракиса ; эти фамилии означают многогранник с 16 треугольными гранями. Это пример дельтаэдра и тела Джонсона .

Двойной многогранник гировытянутой квадратной бипирамиды представляет собой квадратный усеченный трапецоэдр с восемью пятиугольниками и двумя квадратами в качестве граней. Гироудлиненная квадратная пирамида появляется в химии как основа двуглавой квадратной антипризматической молекулярной геометрии , а в математической оптимизации как решение проблемы Томсона .

Строительство

Как и другие гироудлиненные бипирамиды , гироудлиненная квадратная бипирамида может быть построена путем прикрепления двух равносторонних квадратных пирамид к квадратным граням квадратной антипризмы ; этот процесс известен как гироудлинение . Эти пирамиды покрывают каждый квадрат, заменяя его четырьмя равносторонними треугольниками , так что получившийся многогранник имеет в качестве граней 16 равносторонних треугольников. Многогранник, гранями которого являются только равносторонние треугольники, называется дельтаэдром . Существует всего восемь различных выпуклых дельтаэдров, один из которых представляет собой гировытянутую квадратную бипирамиду. В более общем смысле, выпуклый многогранник, в котором все грани правильные, является телом Джонсона , а каждый выпуклый дельтаэдр — телом Джонсона. Гироудлиненная квадратная бипирамида нумеруется среди тел Джонсона как $J_{17}$.

Одна из возможных систем декартовых координат для вершин гировытянутой квадратной бипирамиды, придающая ей длину ребра 2, следующая: $${\begin{aligned}\left(\pm 1,\pm 1,2^{-1/4}\right),\qquad &\left(\pm {\sqrt {2}},0,-2^{-1/4}\right),\\\left(0,\pm {\sqrt {2}},-2^{-1/4}\right),\qquad &\left(0,0,\pm \left(2^{-1/4}+{\sqrt {2}}\right)\right).\end{aligned}}$$

Характеристики

Площадь поверхности гировытянутой квадратной бипирамиды в 16 раз больше площади равностороннего треугольника, то есть: $$4{\sqrt {3}}a^{2}\approx 6.928a^{2},$$а объем гировытянутой квадратной бипирамиды получается путем ее разрезания на две равносторонние квадратные пирамиды и одну квадратную антипризму, а затем сложения их объемов: $${\frac {{\sqrt {2}}+{\sqrt {4+3{\sqrt {2}}}}}{3}}a^{3}\approx 1.428a^{3}.$$

3D модель гировытянутой квадратной бипирамиды

Он имеет ту же трехмерную группу симметрии, что и квадратная антипризма, группа двугранная $D_{4d}$ порядка 8. Его двугранный угол аналогичен гироудлиненной квадратной пирамиде путем расчета суммы равносторонней квадратной пирамиды и угла квадратной антипризмы следующим образом:

• двугранный угол равносторонней квадратной пирамиды между двумя соседними треугольниками, приблизительно $109.47^{\circ }$
• двугранный угол квадратной антипризмы между двумя соседними треугольниками, примерно $127.55^{\circ }$
• двугранный угол между двумя соседними треугольниками на ребре, где равносторонняя квадратная пирамида прикреплена к квадратной антипризме, равен $158.57^{\circ }$, для чего путем сложения двугранных углов между квадратом и треугольником пирамиды и антипризмы.

Двойной многогранник гиродолговатой квадратной бипирамиды представляет собой квадратный усеченный трапецоэдр . Он состоит из восьми пятиугольников и двух квадратов.

Приложение

Гироудлиненную квадратную бипирамиду можно представить в геометрии химических соединений как кластер атомов, окружающий центральный атом в виде многогранника, а состав такого кластера представляет собой двуглавую квадратную антипризматическую молекулярную геометрию . Он имеет 10 вершин и 24 ребра, что соответствует закрытому многограннику с $2n+2$ скелетные электроны. Примером является анион карбида карбонила никеля Ni ₁₀ C(CO). ²⁻
₁₈ , химическое соединение с 22 скелетными электронами, десятью вершинами Ni(CO) ₂ и дефицитом двух монооксидов углерода .

о Задача Томсона конфигурации минимальной энергии $n$ заряженные частицы на сфере. Минимальное решение, известное $n=10$ помещает точки в вершины гировытянутой квадратной бипирамиды, вписанной в сферу .