Гироудлиненная бипирамида
| Гироудлиненная бипирамида | |
|---|---|
 Пятиугольная гировытянутая бипирамида представляет собой правильный икосаэдр . | |
| Лица | 4 n треугольников |
| Края | 6 н |
| Вершины | 2н 2 + |
| Группа симметрии | Д н д , [2 + ,2 n ], (2* n ), порядка 4 n |
| Группа вращения | Д н , [2, н ] + , (22 n ), порядок 2 n |
| Двойной многогранник | усеченные трапецииэдры |
| Характеристики | выпуклый |
В геометрии представляют гироудлиненные бипирамиды собой бесконечное множество многогранников , построенных путем удлинения n- угольной бипирамиды путем вставки n -угольной антипризмы между ее конгруэнтными половинками .
Формы
[ редактировать ]Три члена множества могут быть дельтаэдрами , то есть целиком построенными из равносторонних треугольников : гировытянутая квадратная бипирамида , тело Джонсона ; икосаэдр ; , платоново тело а гировытянутая треугольная бипирамида , если она составлена из равносторонних треугольников, но из-за копланарных граней, не является строго выпуклой. Если пары треугольников слились в ромбы, его можно рассматривать как тригональный трапецоэдр . Остальные элементы могут быть построены из равнобедренных треугольников.
| н | 3 | 4 | 5 | 6 | н |
|---|---|---|---|---|---|
| Тип | Копланарный | Равносторонний | Обычный | Копланарный | |
| Форма | Гироудлиненная треугольная бипирамида | Гироудлиненная квадратная бипирамида | Гироудлиненная пятиугольная бипирамида ( икосаэдр ) | Гироудлиненная шестиугольная бипирамида | Гироудлиненная бипирамида |
| Изображение |  |  |  | 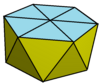 | |
| Лица | 12 | 16 | 20 | 24 | 4 n |
| Двойной | Треугольный усеченный трапецоэдр | Квадратный усеченный трапецоэдр | Пятиугольный усеченный трапецоэдр ( Додекаэдр ) | Шестиугольный усеченный трапецоэдр | Усеченные трапецииэдры |
См. также
[ редактировать ]Внешние ссылки
[ редактировать ]- Обозначение Конвея для многогранников. Попробуйте: «k n A n », где n = 4,5,6... пример «k5A5» — икосаэдр.