Арифметико-логический блок

В вычислительной технике арифметико -логическое устройство ( АЛУ ) представляет собой комбинационную цифровую схему , которая выполняет арифметические и побитовые операции над целыми двоичными числами . ^[1]^[2] В этом отличие от блока с плавающей запятой (FPU), который работает с числами с плавающей запятой . Это фундаментальный строительный блок многих типов вычислительных схем, включая центральный процессор (ЦП) компьютеров, FPU и графические процессоры (GPU). ^[3]

Входными данными для АЛУ являются данные, с которыми нужно работать, называемые операндами , и код, указывающий операцию, которую необходимо выполнить; Выход АЛУ является результатом выполненной операции. Во многих конструкциях АЛУ также имеет входы или выходы состояния, или и то, и другое, которые передают информацию о предыдущей операции или текущей операции соответственно между АЛУ и внешними регистрами состояния .

Сигналы

АЛУ имеет множество входных и выходных цепей , которые представляют собой электрические проводники, используемые для передачи цифровых сигналов между АЛУ и внешней схемой. Когда АЛУ работает, внешние схемы подают сигналы на входы АЛУ, и в ответ АЛУ генерирует и передает сигналы во внешние схемы через свои выходы.

Данные

Базовый АЛУ имеет три параллельные шины данных, состоящие из двух входных операндов ( A и B ) и выходного результата ( Y ). Каждая шина данных представляет собой группу сигналов, передающих одно целое двоичное число. Обычно ширины шин A, B и Y (количество сигналов, составляющих каждую шину) идентичны и соответствуют собственному размеру слова внешней схемы (например, инкапсулирующего ЦП или другого процессора).

Код операции

представляет Входной код операции собой параллельную шину, которая передает в АЛУ код выбора операции, который представляет собой перечислимое значение , определяющее желаемую арифметическую или логическую операцию, которую должно выполнить АЛУ. Размер кода операции (ширина шины) определяет максимальное количество отдельных операций, которые может выполнить АЛУ; например, четырехбитный код операции может определять до шестнадцати различных операций ALU. Как правило, код операции ALU — это не то же самое, что код операции машинного языка , хотя в некоторых случаях он может быть напрямую закодирован как битовое поле внутри кода операции машинного языка.

Статус

Выходы

Выходы состояния представляют собой различные отдельные сигналы, которые передают дополнительную информацию о результате текущей операции АЛУ. АЛУ общего назначения обычно имеют сигналы состояния, такие как:

Вынос , который передает перенос в результате операции сложения, заимствование в результате операции вычитания или бит переполнения в результате операции двоичного сдвига.
Ноль , который указывает, что все биты Y являются логическим нулем.
Negative указывает на то, что результат арифметической операции отрицательный.
Переполнение , которое указывает, что результат арифметической операции вышел за числовой диапазон Y.
Четность , которая указывает, является ли четное или нечетное количество битов в Y логической единицей.

По завершении каждой операции АЛУ выходные сигналы состояния обычно сохраняются во внешних регистрах, чтобы сделать их доступными для будущих операций АЛУ (например, для реализации арифметики с множественной точностью ) или для управления условным ветвлением . Набор битовых регистров, в которых хранятся выходные данные состояния, часто рассматривается как один многоразрядный регистр, который называется «регистром состояния» или «регистром кода состояния».

Входы

Входы состояния позволяют предоставлять дополнительную информацию АЛУ при выполнении операции. Обычно это одиночный бит переноса, который является сохраненным переносом из предыдущей операции АЛУ.

Работа схемы

Комбинационная логическая схема интегральной схемы 74181 , раннего четырехбитного АЛУ, с логическими элементами.

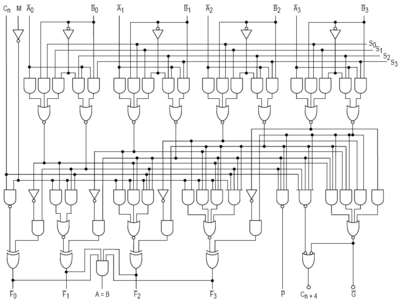
АЛУ представляет собой комбинационную логическую схему, что означает, что его выходные данные будут изменяться асинхронно в ответ на изменения входных данных. При нормальной работе стабильные сигналы подаются на все входы АЛУ, и когда проходит достаточно времени (известное как « задержка распространения ») для распространения сигналов через схему АЛУ, результат работы АЛУ появляется на АЛУ. выходы. Внешняя схема, подключенная к АЛУ, отвечает за обеспечение стабильности входных сигналов АЛУ на протяжении всей операции и за предоставление достаточного времени для распространения сигналов через АЛУ перед выборкой результата АЛУ.

В общем, внешняя схема управляет АЛУ, подавая сигналы на его входы. Обычно внешняя схема использует последовательную логику для управления работой АЛУ, которая регулируется тактовым сигналом достаточно низкой частоты, чтобы обеспечить достаточно времени для выхода АЛУ для стабилизации в наихудших условиях.

Например, ЦП начинает операцию сложения АЛУ, направляя операнды из их источников (которые обычно являются регистрами ) на входы операндов АЛУ, в то время как блок управления одновременно применяет значение к входу кода операции АЛУ, настраивая его для выполнения сложения. В то же время ЦП также направляет выходные данные результата АЛУ в регистр назначения, который получит сумму. Входным сигналам АЛУ, которые остаются стабильными до следующего тактового сигнала, разрешается распространяться через АЛУ и в регистр назначения, пока ЦП ожидает следующего тактового сигнала. Когда поступает следующий тактовый сигнал, регистр назначения сохраняет результат ALU, и, поскольку операция ALU завершена, входы ALU могут быть настроены для следующей операции ALU.

Функции

АЛУ обычно поддерживают ряд основных арифметических и побитовых логических функций. Базовые АЛУ общего назначения обычно включают в свой репертуар следующие операции: ^[1]^[2]^[4]

Арифметические операции

Сложение : A и B суммируются, и сумма появляется в точке Y и выполнении.
Сложение с переносом : A, B и перенос суммируются, и сумма отображается в точках Y и перенос.
Вычитание : B вычитается из A (или наоборот), и разница появляется в точке Y и выполнении. Для этой функции исполнение фактически является индикатором «заимствования». Эту операцию также можно использовать для сравнения величин A и B; в таких случаях вывод Y может быть проигнорирован процессором, которого интересуют только биты состояния (особенно нулевые и отрицательные), возникающие в результате операции.
Вычитание с заимствованием : B вычитается из A (или наоборот) с заимствованием (переносом), и разница появляется в точках Y и выполнения (заимствованием).
Дополнение до двух : A (или B) вычитается из нуля, и разница появляется в Y.
Приращение : A (или B) увеличивается на единицу, и результирующее значение отображается как Y.
Декремент : A (или B) уменьшается на единицу, и результирующее значение отображается как Y.
Прохождение : все биты A (или B) отображаются неизмененными в позиции Y. Эта операция обычно используется для определения четности операнда или того, является ли он нулевым или отрицательным, или для загрузки операнда в регистр процессора.

Побитовые логические операции

AND : побитовое И A и B появляется в Y.
OR : побитовое ИЛИ A и B появляется в Y.
Исключающее-ИЛИ : побитовое исключающее ИЛИ A и B появляется в Y.
Дополнение до единиц : все биты A (или B) инвертируются и появляются в Y.

Операции сдвига битов

Примеры битового сдвига для восьмибитного АЛУ
Тип	Левый	Верно
Арифметический сдвиг
Логический сдвиг
Поворот
Поворот через перенос

Операции сдвига ALU приводят к сдвигу операнда A (или B) влево или вправо (в зависимости от кода операции), и сдвинутый операнд появляется в позиции Y. Простые ALU обычно могут смещать операнд только на одну битовую позицию, тогда как более сложные ALU используют бочкообразные сдвигатели , которые позволяют им сдвигать операнд на произвольное количество бит за одну операцию. Во всех операциях однобитового сдвига бит, сдвинутый из операнда, появляется при выполнении; значение бита, сдвинутого в операнд, зависит от типа сдвига.

Арифметический сдвиг : операнд рассматривается как целое число с дополнением до двух , что означает, что наиболее значимый бит является «знаковым» битом и сохраняется.
Логический сдвиг : в операнд сдвигается логический ноль. Это используется для сдвига целых чисел без знака.
Поворот : операнд рассматривается как кольцевой буфер битов, поэтому его младшие и старшие биты эффективно соседствуют.
Ротация через перенос : бит переноса и операнд вместе обрабатываются как кольцевой буфер битов.

Приложения

Арифметика с множественной точностью

В вычислениях целочисленной арифметики арифметика с множественной точностью — это алгоритм, который работает с целыми числами, превышающими размер слова ALU. Для этого алгоритм рассматривает каждый операнд как упорядоченный набор фрагментов размера ALU, упорядоченных от наиболее значимого (MS) к наименее значимому (LS) или наоборот. Например, в случае 8-битного АЛУ 24-битное целое число 0x123456 будет рассматриваться как набор из трех 8-битных фрагментов: 0x12 (РС), 0x34, и 0x56 (ЛС). Поскольку размер фрагмента точно соответствует размеру слова ALU, ALU может напрямую работать с этим «куском» операнда.

Алгоритм использует ALU для непосредственной работы с определенными фрагментами операндов и, таким образом, генерирует соответствующий фрагмент («частичный») результата с множественной точностью. Каждый партиал при создании записывается в связанную область хранения, предназначенную для результата с множественной точностью. Этот процесс повторяется для всех фрагментов операндов, чтобы создать полную коллекцию частичных значений, что является результатом операции множественной точности.

В арифметических операциях (например, сложении, вычитании) алгоритм начинается с вызова операции ALU над LS-фрагментами операндов, тем самым создавая как частичный LS, так и бит выполнения. Алгоритм записывает часть в назначенное хранилище, тогда как конечный автомат процессора обычно сохраняет бит выполнения в регистр состояния ALU. Затем алгоритм переходит к следующему фрагменту коллекции каждого операнда и вызывает операцию ALU над этими фрагментами вместе с сохраненным битом переноса из предыдущей операции ALU, создавая таким образом еще одну (более значимую) часть и бит выполнения. Как и раньше, бит переноса сохраняется в регистре состояния, а частичный код записывается в назначенное хранилище. Этот процесс повторяется до тех пор, пока не будут обработаны все фрагменты операндов, в результате чего в хранилище сохраняется полный набор частичных значений, которые составляют арифметический результат с высокой точностью.

В операциях сдвига с множественной точностью порядок обработки фрагмента операнда зависит от направления сдвига. При операциях сдвига влево фрагменты сначала обрабатываются LS, поскольку бит LS каждого фрагмента, который передается через сохраненный бит переноса, должен быть получен из бита MS ранее сдвинутого влево менее значимого операнда. И наоборот, операнды сначала обрабатываются MS при операциях сдвига вправо, поскольку бит MS каждого фрагмента должен быть получен из бита LS ранее сдвинутого вправо, более значимого операнда.

В побитовых логических операциях (например, логическом И, логическом ИЛИ) фрагменты операндов могут обрабатываться в любом произвольном порядке, поскольку каждая часть зависит только от соответствующих фрагментов операнда (сохраненный бит переноса из предыдущей операции ALU игнорируется).

Сложные операции

Хотя АЛУ может быть спроектировано для выполнения сложных функций, в результате более высокая сложность схемы, стоимость, энергопотребление и больший размер во многих случаях делают это непрактичным. Следовательно, ALU часто ограничиваются простыми функциями, которые могут выполняться на очень высоких скоростях (т. е. с очень короткими задержками распространения), а схема внешнего процессора отвечает за выполнение сложных функций путем организации последовательности более простых операций ALU.

Например, вычисление квадратного корня числа может быть реализовано различными способами, в зависимости от сложности ALU:

Расчет за один такт : очень сложное АЛУ, которое вычисляет квадратный корень за одну операцию.
Конвейер вычислений : группа простых АЛУ, которая поэтапно вычисляет квадратный корень, при этом промежуточные результаты проходят через АЛУ, организованные как заводская производственная линия . Эта схема может принимать новые операнды до завершения предыдущих и выдавать результаты так же быстро, как и очень сложное АЛУ, хотя результаты задерживаются на сумму задержек распространения каскадов АЛУ. Дополнительные сведения см. в статье о конвейерной обработке инструкций .
Итеративный расчет : простой АЛУ, который вычисляет квадратный корень за несколько шагов под руководством блока управления .

Приведенные выше реализации переходят от самых быстрых и дорогих к самым медленным и наименее затратным. Квадратный корень вычисляется во всех случаях, но процессорам с простыми ALU потребуется больше времени для выполнения вычислений, поскольку необходимо выполнить несколько операций ALU.

Выполнение

АЛУ обычно реализуется либо как отдельная интегральная схема (ИС), например 74181 , либо как часть более сложной ИС. В последнем случае экземпляр ALU обычно создается путем синтеза его описания, написанного на VHDL , Verilog или каком-либо другом языке описания оборудования . Например, следующий код VHDL описывает очень простой 8-битный ALU:

entity alu is
port (  -- the alu connections to external circuitry:
  A  : in signed(7 downto 0);   -- operand A
  B  : in signed(7 downto 0);   -- operand B
  OP : in unsigned(2 downto 0); -- opcode
  Y  : out signed(7 downto 0));  -- operation result
end alu;

architecture behavioral of alu is
begin
 case OP is  -- decode the opcode and perform the operation:
 when "000" =>  Y <= A + B;   -- add
 when "001" =>  Y <= A - B;   -- subtract
 when "010" =>  Y <= A - 1;   -- decrement
 when "011" =>  Y <= A + 1;   -- increment
 when "100" =>  Y <= not A;   -- 1's complement
 when "101" =>  Y <= A and B; -- bitwise AND
 when "110" =>  Y <= A or B;  -- bitwise OR
 when "111" =>  Y <= A xor B; -- bitwise XOR
 when others => Y <= (others => 'X');
 end case;
end behavioral;

История

Математик Джон фон Нейман предложил концепцию ALU в 1945 году в отчете об основах нового компьютера под названием EDVAC . ^[5]

Стоимость, размер и энергопотребление электронных схем были относительно высокими на заре информационной эпохи . Следовательно, все ранние компьютеры имели последовательное АЛУ , которое оперировало одним битом данных за раз, хотя они часто предлагали программистам более широкий размер слова. Первым компьютером, имевшим несколько параллельных дискретных однобитовых схем ALU, был Whirlwind I 1951 года , в котором использовалось шестнадцать таких «математических блоков», что позволяло ему работать с 16-битными словами.

В 1967 году Fairchild представила первое ALU-подобное устройство, реализованное в виде интегральной схемы, Fairchild 3800, состоящее из восьмибитного арифметического устройства с аккумулятором. Он поддерживал только сложение и вычитание, но не поддерживал логические функции. ^[6]

Вскоре появились полноценные ALU на интегральных схемах, в том числе четырехбитные ALU, такие как Am2901 и 74181 . Эти устройства обычно были способны к « битовому срезу », то есть имели сигналы «переноса вперед», что облегчало использование нескольких взаимосвязанных микросхем ALU для создания ALU с более широким размером слова. Эти устройства быстро стали популярными и широко использовались в побитовых мини-компьютерах.

Микропроцессоры начали появляться в начале 1970-х годов. Несмотря на то, что транзисторы стали меньше, иногда на кристалле было недостаточно места для АЛУ полной ширины слова, и в результате в некоторых ранних микропроцессорах использовалось узкое АЛУ, которое требовало нескольких циклов на одну инструкцию машинного языка. Примером этого может служить популярный Zilog Z80 , который выполнял восьмибитное сложение с помощью четырехбитного АЛУ. ^[7] Со временем геометрия транзисторов еще больше уменьшилась, следуя закону Мура , и стало возможным создавать более широкие АЛУ на микропроцессорах.

Транзисторы современных интегральных схем (ИС) на несколько порядков меньше, чем у ранних микропроцессоров, что позволяет устанавливать на ИС весьма сложные АЛУ. Сегодня многие современные ALU имеют большую ширину слова и архитектурные усовершенствования, такие как бочкообразные переключатели и двоичные умножители , которые позволяют им выполнять за один такт операции, которые на более ранних ALU требовали нескольких операций.

АЛУ могут быть реализованы как механические , электромеханические или электронные схемы. ^[8]^{[ не удалось пройти проверку ]} и в последние годы были проведены исследования биологических ALU. ^[9]^[10] (например, на основе актина ). ^[11]

См. также

Ссылки

^ Перейти обратно: ^а ^б Атул П. Годзе; Дипали А. Годзе (2009). «3» . Проектирование цифровой логики . Технические публикации. стр. 9–3. ISBN 978-81-8431-738-1 . ^{[ постоянная мертвая ссылка ]}
^ Перейти обратно: ^а ^б Атул П. Годзе; Дипали А. Годзе (2009). «Приложение». Цифровые логические схемы . Технические публикации. стр. C–1. ISBN 978-81-8431-650-6 . ^{[ постоянная мертвая ссылка ]}
^ «1. Введение в компьютерную архитектуру. Проектирование встраиваемого оборудования, 2-е издание [Книга]» . www.oreilly.com . Проверено 3 сентября 2020 г.
^ Горовиц, Пол ; Уинфилд Хилл (1989). «14.1.1». Искусство электроники (2-е изд.). Издательство Кембриджского университета. стр. 990–. ISBN 978-0-521-37095-0 .
^ Филип Левис (8 ноября 2004 г.). «Джонатан фон Нейман и EDVAC» (PDF) . cs.berkeley.edu . стр. 1, 3. Архивировано из оригинала (PDF) 23 сентября 2015 года . Проверено 20 января 2015 г.
^ Шериф, Кен. «Внутри чипа ALU 74181: фотографии кристалла и реверс-инжиниринг» . Блог Кена Ширриффа . Проверено 7 мая 2024 г.
^ Кен Ширрифф. «Z-80 имеет 4-битное ALU. Вот как оно работает». 2013, righto.com
^ Рейф, Джон Х. (2009), «Механические вычисления: вычислительная сложность физических устройств» , Мейерс, Роберт А. (редактор), Энциклопедия сложности и системных наук , Нью-Йорк, Нью-Йорк: Springer, стр. 5466– 5482, номер домена : 10.1007/978-0-387-30440-3_325 , ISBN 978-0-387-30440-3 , получено 03 сентября 2020 г.
^ Линь, Чунь-Лян; Куо, Тин-Ю; Ли, Вэй-Сянь (14 августа 2018 г.). «Синтез блока управления биокомпьютера будущего» . Журнал биологической инженерии . 12 (1): 14. дои : 10.1186/s13036-018-0109-4 . ISSN 1754-1611 . ПМК 6092829 . ПМИД 30127848 .
^ Герд Хг Мо-Беренс. «Биологический микропроцессор, или как построить компьютер из биологических частей» .
^ Дас, Биплаб; Пол, Авиджит Кумар; Де, Дебашис (16 августа 2019 г.). «Разработка и вычисления нетрадиционного арифметико-логического устройства в актиновых квантовых клеточных автоматах» . Микросистемные технологии . 28 (3): 809–822. дои : 10.1007/s00542-019-04590-1 . ISSN 1432-1858 . S2CID 202099203 .

Дальнейшее чтение

Хван, Енох (2006). Цифровая логика и проектирование микропроцессоров с использованием VHDL . Томсон. ISBN 0-534-46593-5 .
Столлингс, Уильям (2006). Компьютерная организация и архитектура: проектирование для повышения производительности (7-е изд.). Пирсон Прентис Холл. ISBN 0-13-185644-8 .

Внешние ссылки

[A.P.GodseD.A.Godse2009-1] Перейти обратно: ^а ^б Атул П. Годзе; Дипали А. Годзе (2009). «3» . Проектирование цифровой логики . Технические публикации. стр. 9–3. ISBN 978-81-8431-738-1 . ^{[ постоянная мертвая ссылка ]}

[A.P.GodseD.A.Godse2009-2-2] Перейти обратно: ^а ^б Атул П. Годзе; Дипали А. Годзе (2009). «Приложение». Цифровые логические схемы . Технические публикации. стр. C–1. ISBN 978-81-8431-650-6 . ^{[ постоянная мертвая ссылка ]}

[3] «1. Введение в компьютерную архитектуру. Проектирование встраиваемого оборудования, 2-е издание [Книга]» . www.oreilly.com . Проверено 3 сентября 2020 г.

[hh-4] Горовиц, Пол ; Уинфилд Хилл (1989). «14.1.1». Искусство электроники (2-е изд.). Издательство Кембриджского университета. стр. 990–. ISBN 978-0-521-37095-0 .

[5] Филип Левис (8 ноября 2004 г.). «Джонатан фон Нейман и EDVAC» (PDF) . cs.berkeley.edu . стр. 1, 3. Архивировано из оригинала (PDF) 23 сентября 2015 года . Проверено 20 января 2015 г.

[6] Шериф, Кен. «Внутри чипа ALU 74181: фотографии кристалла и реверс-инжиниринг» . Блог Кена Ширриффа . Проверено 7 мая 2024 г.

[7] Кен Ширрифф. «Z-80 имеет 4-битное ALU. Вот как оно работает». 2013, righto.com

[8] Рейф, Джон Х. (2009), «Механические вычисления: вычислительная сложность физических устройств» , Мейерс, Роберт А. (редактор), Энциклопедия сложности и системных наук , Нью-Йорк, Нью-Йорк: Springer, стр. 5466– 5482, номер домена : 10.1007/978-0-387-30440-3_325 , ISBN 978-0-387-30440-3 , получено 03 сентября 2020 г.

[9] Линь, Чунь-Лян; Куо, Тин-Ю; Ли, Вэй-Сянь (14 августа 2018 г.). «Синтез блока управления биокомпьютера будущего» . Журнал биологической инженерии . 12 (1): 14. дои : 10.1186/s13036-018-0109-4 . ISSN 1754-1611 . ПМК 6092829 . ПМИД 30127848 .

[10] Герд Хг Мо-Беренс. «Биологический микропроцессор, или как построить компьютер из биологических частей» .

[11] Дас, Биплаб; Пол, Авиджит Кумар; Де, Дебашис (16 августа 2019 г.). «Разработка и вычисления нетрадиционного арифметико-логического устройства в актиновых квантовых клеточных автоматах» . Микросистемные технологии . 28 (3): 809–822. дои : 10.1007/s00542-019-04590-1 . ISSN 1432-1858 . S2CID 202099203 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]