Плоский модуль

В алгебре к плоским модулям относятся свободные модули , проективные модули и, в области главных идеалов , модули без кручения . Формально модуль M над кольцом R является плоским, если тензорное произведение над R с M сохраняет точные последовательности . Модуль является абсолютно плоским , если тензорное произведение с последовательностью дает точную последовательность тогда и только тогда, когда исходная последовательность точна.

Плоскостность была введена Жаном-Пьером Серром ( 1956 ) в его статье «Алгебричная геометрия и аналитическая геометрия» .

Определение

Левый модуль M над кольцом R является плоским, если выполнено следующее условие: для любого инъективного линейного отображения $\varphi :K\to L$ правых R -модулей отображение

$\varphi \otimes _{R}M:K\otimes _{R}M\to L\otimes _{R}M$

также инъективен, где $\varphi \otimes _{R}M$это карта индуцированный $k\otimes m\mapsto \varphi (k)\otimes m.$

Для этого определения достаточно ограничить инъекции $\varphi$ к включениям конечно порожденных идеалов в R .

Эквивалентно, R -модуль M является плоским, если тензорное произведение с M является точным функтором ; то есть если для каждой короткой точной -модулей R последовательности $0\rightarrow K\rightarrow L\rightarrow J\rightarrow 0,$ последовательность $0\rightarrow K\otimes _{R}M\rightarrow L\otimes _{R}M\rightarrow J\otimes _{R}M\rightarrow 0$тоже точно. (Это эквивалентное определение, поскольку тензорное произведение является точным правым функтором .)

Эти определения применимы и в том случае, если R — некоммутативное кольцо, а M — левый R -модуль; в этом случае K , L и J должны быть правыми R -модулями, а тензорные произведения не являются R вообще -модулями, а лишь абелевыми группами .

Характеристики

Плоскостность также можно охарактеризовать следующим эквациональным условием, означающим, что R - линейные отношения в M вытекают из линейных отношений в R .

Левый R -модуль M плоский тогда и только тогда, когда для любого линейного отношения

${\textstyle \sum _{i=1}^{m}r_{i}x_{i}=0}$

с $r_{i}\in R$ и $x_{i}\in M$, существуют элементы $y_{j}\in M$ и $a_{i,j}\in R,$ такой, что

${\textstyle \sum _{i=1}^{m}r_{i}a_{i,j}=0\qquad }$ для $j=1,\ldots ,n,$

и

${\textstyle x_{i}=\sum _{j=1}^{n}a_{i,j}y_{j}\qquad }$ для $i=1,\ldots ,m.$

Это эквивалентно определению n элементов модуля и линейной карты из $R^{n}$ этому модулю, который отображает стандартную основу $R^{n}$к n элементам. Это позволяет переписать предыдущую характеристику в терминах гомоморфизмов следующим образом.

R отображения -модуль M плоский тогда и только тогда, когда выполнено следующее условие: для всякого $f:F\to M,$ где $F$ является конечно порожденным свободным R -модулем, и для каждого конечно порожденного R -подмодуля $K$ из $\ker f,$ карта $f$ факторы через отображение g в свободный R -модуль $G$ такой, что $g(K)=0:$

Factor property of a flat module

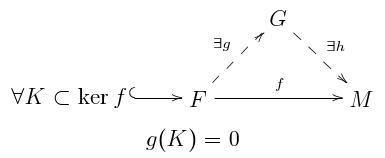
Отношения с другими свойствами модуля

Плоскостность связана с различными другими свойствами модуля, такими как свобода, проективность или отсутствие кручения. В частности, каждый плоский модуль не имеет кручения , каждый проективный модуль плоский и каждый свободный модуль проективен.

Существуют конечно порожденные модули , плоские и непроективные. Однако все конечно порожденные плоские модули проективны над наиболее часто рассматриваемыми кольцами. Более того, конечно порожденный модуль является плоским тогда и только тогда, когда он локально свободен , то есть все локализации в простых идеалах являются свободными модулями.

Частично это отражено на следующем рисунке.

Module properties in commutative algebra

Модули без кручения

Каждый плоский модуль не имеет скручивания . Это следует из приведенной выше характеристики в терминах отношений, принимая m = 1 .

Обратное справедливо для целых чисел и, в более общем смысле, для областей главных идеалов и дедекиндовых колец .

Область целостности, в которой каждый модуль без кручения плоский, называется областью Прюфера .

Свободные и проективные модули

Модуль M проективен тогда и только тогда , когда существует свободный модуль G и два линейных отображения. $i:M\to G$ и $p:G\to M$ такой, что $p\circ i=\mathrm {id} _{M}.$ В частности, всякий свободный модуль проективен (возьмем $G=M$ и $i=p=\mathrm {id} _{M}$).

Каждый проективный модуль плоский. Это можно доказать на основе приведенных выше характеристик плоскостности и проективности в терминах линейных отображений, взяв $g=i\circ f$ и $h=p.$

И наоборот, конечно порожденные плоские модули проективны при мягких условиях, которые обычно выполняются в коммутативной алгебре и алгебраической геометрии . Это делает концепцию плоскостности полезной в основном для модулей, которые не являются конечно сгенерированными.

Конечно определенный модуль (то есть фактор конечно порожденного свободного модуля по конечно порожденному подмодулю), который является плоским, всегда проективен. Это можно доказать, взяв f сюръективно и $K=\ker f$в приведенной выше характеристике плоскостности в терминах линейных отображений. Состояние $g(K)=0$ подразумевает существование линейного отображения $i:M\to G$ такой, что $i\circ f=g,$ и поэтому $h\circ i\circ f=h\circ g=f.$ Поскольку f сюръективно, то, таким образом, имеем $h\circ i=\mathrm {id} _{M},$ и M проективно.

Над нетеровым кольцом каждый конечно порожденный плоский модуль проективен, поскольку каждый конечно порожденный модуль конечно представим. Тот же результат верен и для области целостности , даже если она не нётерова.

На локальном кольце каждый конечно порожденный плоский модуль свободен.

Конечно порожденный плоский модуль, который не является проективным, можно построить следующим образом. Позволять $R=F^{\mathbb {N} }$— множество бесконечных последовательностей , члены которых принадлежат фиксированному полю F . Это коммутативное кольцо, в котором сложение и умножение определены покомпонентно. Это кольцо абсолютно плоское (т. е. каждый модуль плоский). Модуль $R/I,$ где I — идеал последовательностей с конечным числом ненулевых членов, таким образом, является плоским и конечно порожденным (только один генератор), но не проективным.

Непримеры

• Если I — идеал в нётеровом коммутативном кольце R , то $R/I$не является плоским модулем, за исключением случаев, когда I порождается идемпотентом ( то есть элементом, равным его квадрату). В частности, если R — область целостности , $R/I$ является плоским, только если $I$ равен R или является нулевым идеалом .
• В области целостности плоский модуль не имеет кручения . Таким образом, модуль, содержащий ненулевые элементы кручения, не является плоским. В частности $\mathbb {Q} /\mathbb {Z}$ и все поля положительных характеристик неплоские $\mathbb {Z}$-модули, где $\mathbb {Z}$ — кольцо целых чисел, а $\mathbb {Q}$ – поле рациональных чисел.

Прямые суммы, лимиты и продукты

Прямая сумма $\textstyle \bigoplus _{i\in I}M_{i}$ модулей является плоским тогда и только тогда, когда каждый $M_{i}$ плоский.

Прямым пределом флэта является флет. В частности, прямой предел свободных модулей является плоским. И наоборот, каждый плоский модуль можно записать как прямой предел конечно порожденных свободных модулей.

Прямые произведения плоских модулей вообще не обязательно должны быть плоскими. Фактически, для кольца R каждое прямое произведение плоских R -модулей является плоским тогда и только тогда, когда R — когерентное кольцо (т. е. каждый конечно порожденный идеал конечно представим).

Удлинители плоских колец

Кольцевой гомоморфизм $R\to S$является плоским , если S — плоский R -модуль для модульной структуры, индуцированной гомоморфизмом. Например, кольцо полиномов R [ t ] плоское над R для любого R. кольца

Для любого мультипликативного подмножества $S$ коммутативного кольца $R$, локализация $S^{-1}R$является плоской R - алгеброй (она проективна лишь в исключительных случаях). Например, $\mathbb {Q}$ плоский и не проективный относительно $\mathbb {Z} .$

Если $I$ является идеалом нетерова коммутативного кольца $R,$ завершение ​ ${\widehat {R}}$ из $R$ относительно $I$ плоский. Оно истинно плоское тогда и только тогда, когда $I$ содержится в Джекобсона радикале $A.$ (См. также кольцо Зариского .)

Местная собственность

В этом разделе R обозначает коммутативное кольцо . Если ${\mathfrak {p}}$ является простым R в , локализация идеалом ${\mathfrak {p}}$ как обычно обозначается ${\mathfrak {p}}$как индекс. То есть, $R_{\mathfrak {p}}=(R\setminus {\mathfrak {p}})^{-1}R,$ и, если M — R -модуль, $M_{\mathfrak {p}}=(R\setminus {\mathfrak {p}})^{-1}M=R_{\mathfrak {p}}\otimes _{R}M.$

Если M — R -модуль, то три следующих условия эквивалентны:

• $M$ это квартира $R$-модуль;
• $M_{\mathfrak {p}}$ это квартира $R_{\mathfrak {p}}$-модуль для каждого простого идеала ${\mathfrak {p}};$
• $M_{\mathfrak {m}}$ это квартира $R_{\mathfrak {m}}$-модуль для каждого максимального идеала ${\mathfrak {m}}.$

Это свойство является фундаментальным в коммутативной алгебре и алгебраической геометрии, поскольку оно сводит изучение плоскости к случаю локальных колец . Они часто выражаются в том, что плоскостность является локальным свойством .

Плоские морфизмы схем

Определение плоского морфизма схем непосредственно вытекает из локального свойства плоскости.

Морфизм $f:X\to Y$ схем , является плоским морфизмом если индуцированное отображение на локальных кольцах

${\mathcal {O}}_{Y,f(x)}\to {\mathcal {O}}_{X,x}$

является плоским гомоморфизмом колец для любой точки x из X .

Таким образом, свойства плоских (или точно плоских) гомоморфизмов колец естественным образом распространяются на геометрические свойства плоских морфизмов в алгебраической геометрии.

Например, рассмотрим квартиру $\mathbb {C} [t]$-алгебра $R=\mathbb {C} [t,x,y]/(xy-t)$(см. ниже). Включение $\mathbb {C} [t]\hookrightarrow R$ индуцирует плоский морфизм

$\pi :\operatorname {Spec} (R)\to \operatorname {Spec} (\mathbb {C} [t]).$

Каждое (геометрическое) волокно $\pi ^{-1}(t)$ представляет собой кривую уравнения $xy=t.$ (См. также плоскую дегенерацию и деформацию до нормального конуса .)

Позволять $S=R[x_{1},\dots ,x_{r}]$ — кольцо полиномов над коммутативным нётеровым кольцом $R$ и $f\in S$ненулевой делитель. Затем $S/fS$ плоский $R$ если и только если $f$ примитивен ( коэффициенты порождают единичный идеал). Примером является $\mathbb {C} [t,x,y]/(xy-t),$ который является плоским (и даже бесплатным) в течение $\mathbb {C} [t]$(геометрический смысл см. также ниже). Такие плоские расширения можно использовать для получения примеров плоских модулей, которые не являются бесплатными и не являются результатом локализации.

Верная плоскостность

Модуль является абсолютно плоским , если тензорное произведение с последовательностью дает точную последовательность тогда и только тогда, когда исходная последовательность точна. Хотя это понятие определено для модулей над необязательным коммутативным кольцом, оно используется в основном для коммутативных алгебр . Итак, это единственный случай, который здесь рассматривается, даже если некоторые результаты можно обобщить на случай модулей над некоммутативным кольцом.

В этой секции, $f\colon R\to S$ является кольцевым гомоморфизмом коммутативных колец, который дает $S$ структуры $R$-алгебра и $R$-модуль. Если $S$ это $R$-модуль плоский (или совершенно плоский), обычно говорят, что $S$ является плоским (или совершенно плоским) над $R,$ и это $f$ плоский (или совершенно плоский).

Если $S$ плоский $R,$ следующие условия эквивалентны.

• $S$ действительно плоский.
• Для каждого максимального идеала ${\mathfrak {m}}$ из $R$, надо ${\mathfrak {m}}S\neq S.$
• Если $M$ ненулевое значение $R$-модуль, то $M\otimes _{R}S\neq 0.$
• Для каждого простого идеала ${\mathfrak {p}}$ из $R,$ есть главный идеал ${\mathfrak {P}}$ из $S$ такой, что ${\mathfrak {p}}=f^{-1}({\mathfrak {P}}).$ Другими словами, карта $f^{*}\colon \operatorname {Spec} (S)\to \operatorname {Spec} (R)$ индуцированный $f$ на спектрах сюръективен.
• $f,$ является инъективным, и $R$ является чистым подкольцом $S;$ то есть, $M\to M\otimes _{R}S$ инъективен для каждого $R$-модуль $M$.

Из второго условия следует, что плоский локальный гомоморфизм локальных колец строго плоский. Из последнего условия следует, что $I=IS\cap R$ для каждого идеала $I$ из $R$ (брать $M=R/I$). В частности, если $S$ является нётеровым кольцом, то $R$ также нётеровский.

Предпоследнее условие можно сформулировать в следующей усиленной форме: $\operatorname {Spec} (S)\to \operatorname {Spec} (R)$ является субмерсивным , что означает, что Зарисского топология $\operatorname {Spec} (R)$ является топологии фактортопологией $\operatorname {Spec} (S)$ (это частный случай того, что таким свойством обладает точно плоский квазикомпактный морфизм схем. ). См. также Плоский морфизм § Свойства плоских морфизмов .

Примеры

• Кольцевой гомоморфизм $R\to S$ такой, что $S$является ненулевым свободным R -модулем, является строго плоским. Например:
  • Каждое расширение поля является абсолютно плоским. Это свойство неявно лежит в основе использования комплексификации для доказательства результатов в действительных векторных пространствах.
  • Кольцо многочленов является точно плоским расширением своего кольца коэффициентов.
  • Если $p\in R[x]$ — монический полином , включение $R\hookrightarrow R[t]/\langle p\rangle$ действительно плоский.
• Позволять $t_{1},\ldots ,t_{k}\in R.$ Прямой продукт $\textstyle \prod _{i}R[t_{i}^{-1}]$ локализаций ​ на $t_{i}$ верно плоская $R$ если и только если $t_{1},\ldots ,t_{k}$ сгенерировать идеал единичный $R$ (то есть, если $1$ представляет собой линейную комбинацию $t_{i}$).
• Прямая сумма локализаций $R_{\mathfrak {p}}$ из $R$ при всех своих простых идеалах является строго плоским модулем, который не является алгеброй, за исключением случаев, когда простых идеалов конечное число.

Два последних примера неявно лежат в основе широкого использования локализации в коммутативной алгебре и алгебраической геометрии.

• Для данного кольцевого гомоморфизма $f:A\to B,$ существует связанный комплекс, называемый комплексом Амицура :

$$0\to A{\overset {f}{\to }}B{\overset {\delta ^{0}}{\to }}B\otimes _{A}B{\overset {\delta ^{1}}{\to }}B\otimes _{A}B\otimes _{A}B\to \cdots$$

где кограничные операторы $\delta ^{n}$— чередующиеся суммы карт, полученные вставкой 1 в каждую точку; например, $\delta ^{0}(b)=b\otimes 1-1\otimes b$. Тогда (Гротендик) этот комплекс точен, если $f$ действительно плоский.

локальные

Вот одна из характеристик строго плоского гомоморфизма для не обязательно плоского гомоморфизма. Учитывая инъективный локальный гомоморфизм $(R,{\mathfrak {m}})\hookrightarrow (S,{\mathfrak {n}})$ такой, что ${\mathfrak {m}}S$ является ${\mathfrak {n}}$- первичный идеал , гомоморфизм $S\to B$является точно плоским тогда и только тогда, когда теорема перехода для него справедлива ; то есть для каждого ${\mathfrak {m}}$-первичный идеал ${\mathfrak {q}}$ из $R$, $\operatorname {length} _{S}(S/{\mathfrak {q}}S)=\operatorname {length} _{S}(S/{\mathfrak {m}}S)\operatorname {length} _{R}(R/{\mathfrak {q}}).$

Гомологическая характеристика с

Плоскостность также можно выразить с помощью функторов Tor — левых производных функторов тензорного произведения. левый $R$-модуль $M$ является плоским тогда и только тогда, когда

$\operatorname {Tor} _{n}^{R}(X,M)=0$ для всех $n\geq 1$ и все в порядке $R$-модули $X$).

На самом деле достаточно проверить, что первый член Tor равен нулю, т. е. M плоско тогда и только тогда, когда

$\operatorname {Tor} _{1}^{R}(N,M)=0$

для любого $R$-модуль $N$ или, еще более ограничительно, когда $N=R/I$ и $I\subset R$ — любой конечно порожденный идеал.

функтора Tor Используя длинные точные последовательности , можно легко доказать факты о короткой точной последовательности.

$0\to A{\overset {f}{\longrightarrow }}B{\overset {g}{\longrightarrow }}C\to 0$

Если $A$ и $C$ плоские, то и так $B$. Кроме того, если $B$ и $C$ плоские, то и так $A$. Если $A$ и $B$ плоские, $C$в целом не обязательно должен быть плоским. Однако, если $A$ чист ​ в $B$ и $B$ плоский, то $A$ и $C$ плоские.

Плоские разрешения

Плоское разрешение модуля $M$ представляет собой разрешение вида

$\cdots \to F_{2}\to F_{1}\to F_{0}\to M\to 0,$

где $F_{i}$все плоские модули. Любая свободная или проективная резолюция обязательно является плоской резолюцией. Плоские разрешения можно использовать для вычисления функтора Tor .

Длина что конечного плоского разрешения — это первый индекс n такой, $F_{n}$ ненулевое значение и $F_{i}=0$ для $i>n$. Если модуль $M$ допускает конечную плоскую резолюцию, минимальную длину среди всех конечных плоских резольвент $M$ называется его плоским размером и обозначили $\operatorname {fd} (M)$. Если $M$не допускает конечного плоского разрешения, то по соглашению плоская размерность называется бесконечной. В качестве примера рассмотрим модуль $M$ такой, что $\operatorname {fd} (M)=0$. В этой ситуации точность последовательности $0\to F_{0}\to M\to 0$ указывает на то, что стрелка в центре является изоморфизмом и, следовательно, $M$ сам по себе плоский.

В некоторых областях теории модулей плоское разрешение должно удовлетворять дополнительному требованию, чтобы каждое отображение было плоским предварительным покрытием ядра отображения справа. Для проективных резольвент это условие почти незаметно: проективное преднакрытие — это просто эпиморфизм проективного модуля. Эти идеи вдохновлены работой Ауслендера по приближениям. Эти идеи также знакомы из более распространенного понятия минимальных проективных резольвент, где каждое отображение должно быть проективным покрытием ядра отображения справа. Однако проективные покрытия вообще не обязательно должны существовать, поэтому минимальные проективные разрешения имеют лишь ограниченное применение в кольцах, таких как целые числа.

Плоские обложки

Хотя проективные покрытия модулей не всегда существуют, предполагалось, что для общих колец каждый модуль будет иметь плоское покрытие, то есть каждый модуль M будет эпиморфным образом плоского модуля F , таким что каждое отображение плоского модуля на M факторизуется через F , и любой эндоморфизм F над M является автоморфизмом. Гипотеза о плоском покрытии была впервые сформулирована в явном виде у Еноха ( 1981 , стр. 196). Гипотеза оказалась верной, решена положительно и доказана одновременно Л. Биканом, Р. Эль-Баширом и Э. Енохсом. Этому предшествовали важные вклады П. Эклофа, Дж. Трлифая и Дж. Сюй.

Поскольку плоские накрытия существуют для всех модулей над всеми кольцами, минимальные плоские резольвенты во многих случаях могут заменить минимальные проективные резольвенты. Измерение отклонения плоских резолюций от проективных резолюций называется относительной гомологической алгеброй и описано в таких классических работах, как Мак Лейн ( 1963 ), а также в более поздних работах, посвященных плоским резольвентам, таких как Енохс и Дженда ( 2000 ).

В конструктивной математике

Плоские модули приобретают все большее значение в конструктивной математике , где проективные модули менее полезны. Например, то, что все свободные модули проективны, эквивалентно полной аксиоме выбора , поэтому теоремы о проективных модулях, даже если они доказаны конструктивно, не обязательно применимы к свободным модулям. Напротив, для доказательства того, что свободные модули плоские, не требуется никакого выбора, поэтому теоремы о плоских модулях по-прежнему применимы.

См. также

• Общая плоскостность
• Плоский морфизм
• Регулярное кольцо фон Неймана – кольца, над которыми все модули плоские.
• Обычно плоское кольцо

Ссылки

• Артин. «Теория деформации» (PDF) . Архивировано (PDF) из оригинала 18 ноября 2019 года.
• Артин, Майкл (1999). «Некоммутативные кольца» (PDF) .
• Бикан, Л.; Эль Башир, Р.; Енохс, Э. (2001), «Все модули имеют плоские крышки», Bull. Лондонская математика. Соц. , 33 (4): 385–390, doi : 10.1017/S0024609301008104 , ISSN   0024-6093 , MR   1832549
• Картье, Пьер (1958). «Вопросы рациональности делителей в алгебраической геометрии» . Бюллетень Математического общества Франции (на французском языке). 86 : 177–251. дои : 10.24033/bsmf.1503 .
• Бурбаки, Николя . Коммутативная алгебра .
• Чейз, Стивен У. (1960), «Прямое произведение модулей», Transactions of the American Mathematical Society , 97 (3): 457–473, doi : 10.2307/1993382 , JSTOR   1993382 , MR   0120260
• Эйзенбуд, Дэвид (1995), Коммутативная алгебра , Тексты для аспирантов по математике , том. 150, Берлин, Нью-Йорк: Springer-Verlag , номер номера : 10.1007/978-1-4612-5350-1 , ISBN.  978-0-387-94268-1 , МР   1322960
• Енохс, Эдгар Э. (1981), «Инъективные и плоские покрытия, конверты и резольвенты», Израильский журнал математики , 39 (3): 189–209, doi : 10.1007/BF02760849 , ISSN   0021-2172 , MR   0636889 , S2CID   120567780
• Енохс, Эдгар Э.; Дженда, Овертаун М.Г. (2000), Относительная гомологическая алгебра , Изложения де Грюйтера по математике, том. 30, Берлин: Вальтер де Грюйтер и компания, номер номера : 10.1515/9783110803662 , ISBN.  978-3-11-016633-0 , МР   1753146
• Кунц, Эрнст (1969), «Характеристики регулярных локальных колец характеристики p », American Journal of Mathematics , 91 (3): 772–784, doi : 10.2307/2373351 , JSTOR   2373351 , MR   0252389
• Лам, Цит-Юэн (1999), Лекции по модулям и кольцам , Тексты для аспирантов по математике № 189, том. 189, Берлин, Нью-Йорк: Springer-Verlag , номер номера : 10.1007/978-1-4612-0525-8 , ISBN.  978-0-387-98428-5 , МР   1653294
• Лазар, Даниэль (1969), «Вокруг банальности» , Bulletin de la Société Mathématique de France , 97 : 81–128, doi : 10.24033/bsmf.1675
• Мак Лейн, Сондерс (1963), Гомология , Фундаментальные принципы математических наук, Том 114, Бостон, Массачусетс: Academic Press , MR   0156879.
• Мацумура, Хидеюки (1970), Коммутативная алгебра
• Мацумура, Хидеюки (1986). Коммутативная теория колец . Кембриджские исследования по высшей математике. Том. 8. Издательство Кембриджского университета. ISBN  0-521-36764-6 . МР   0879273 . Збл   0603.13001 .
• Мамфорд, Дэвид , Красная книга сортов и схем.
• Норткотт, Д.Г. (1984), Полилинейная алгебра , издательство Кембриджского университета , стр. 33, ISBN  978-0-521-26269-9
• Ричман, Фред (1997), «Плоская размерность, конструктивность и теорема о сизигиях Гильберта», New Zealand Journal of Mathematics , 26 (2): 263–273, ISSN   1171-6096 , MR   1601663
• SGA 1 , Exposé VIII – это основная ссылка (но она зависит от результата Жиро (1964), который заменил (в гораздо более общей форме) неопубликованное Exposé VII SGA1)
• Серр, Жан-Пьер (1956), «Алгебраическая геометрия и аналитическая геометрия» , Annales de l'Institut Fourier , 6 : 1–42, doi : 10.5802/aif.59 , ISSN   0373-0956 , MR   0082175