Инъекционный модуль

В математике , особенно в области абстрактной алгебры , известной как теория модулей , инъективный модуль — это модуль Q , который разделяет определенные желательные свойства с Z -модулем Q всех рациональных чисел . В частности, если Q — подмодуль какого-либо другого модуля, то он уже является прямым слагаемым этого модуля; Кроме того, для данного подмодуля модуля Y любой гомоморфизм модуля из этого подмодуля в Q может быть расширен до гомоморфизма всего Y в Q . Эта концепция двойственна концепции проективных модулей . Инъективные модули были введены в ( Baer 1940 ) и довольно подробно обсуждаются в учебнике ( Lam 1999 , §3).

Инъективные модули тщательно изучены, и в их терминах определяется множество дополнительных понятий: Инъективные когенераторы — это инъективные модули, которые точно представляют всю категорию модулей. Инъективные разрешения измеряют, насколько далек от инъективного модуль с точки зрения инъективной размерности, и представляют модули в производной категории . Инъективные оболочки являются максимальными существенными расширениями и оказываются минимальными инъективными расширениями. Над нетеровым кольцом каждый инъективный модуль является однозначно прямой суммой неразложимых модулей, и их структура хорошо понятна. Инъективный модуль над одним кольцом может не быть инъективным над другим, но существуют хорошо изученные методы замены колец, которые обрабатывают особые случаи. Кольца, которые сами по себе являются инъективными модулями, обладают рядом интересных свойств и включают в себя такие кольца, как групповые кольца конечных групп над полями . Инъективные модули включают делимые группы и обобщаются понятием инъективных объектов. в теории категорий .

Определение

Левый модуль Q над кольцом R инъективен, если он удовлетворяет одному (и, следовательно, всем) из следующих эквивалентных условий:

Если Q — подмодуль некоторого другого левого R -модуля M , то существует другой подмодуль K модуля M такой, что M — внутренняя прямая сумма Q и K , т. е. Q + K = M и Q ∩ K = {0}.
Любая короткая точная последовательность 0 → Q → M → K → 0 левых R -модулей расщепляется .
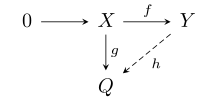
Если X и Y — левые R -модули, f : X → Y — инъективный гомоморфизм модулей и g : X → Q — произвольный гомоморфизм модулей, то существует гомоморфизм модулей h : Y → Q такой, что hf = g , т. е. такая, что следующая диаграмма коммутирует :

Контравариантный левых функтор Hom (-, Q ) из категории -модулей R в категорию абелевых групп точен Hom .

Инъективные правые R -модули определяются совершенно аналогично.

Примеры

Первые примеры

Тривиально, нулевой модуль {0} инъективен.

Для данного поля k каждое k - векторное пространство Q является инъективным k -модулем. Причина: если — V , мы можем найти базис Q Q и расширить его до базиса V. подпространство Новые расширяющиеся базисные векторы охватывают подпространство K пространства V а V является внутренней прямой суммой Q и K. , Обратите внимание, что прямое дополнение K к Q не определяется однозначно Q , и аналогично расширяющееся отображение h в приведенном выше определении обычно не уникально.

Рациональные числа Q (с добавлением) образуют инъективную абелеву группу (т. е. инъективный Z -модуль). Фактор -группа Q / Z и группа круга также являются инъективными Z -модулями. Фактор-группа Z / n Z при n > 1 инъективна как Z / n Z -модуль, но не инъективна как абелева группа.

Коммутативные примеры

В более общем смысле, для любой области целостности R с полем частных K R R -модуль K является инъективным R -модулем и даже наименьшим инъективным R содержащим -модулем , . Для любой дедекиндовой области фактормодуль K слагаемые / R также инъективен, а его неразложимые являются локализациями $R_{\mathfrak {p}}/R$ для ненулевых простых идеалов ${\mathfrak {p}}$ . Нулевой идеал также является простым и соответствует инъективному K . Таким образом, между простыми идеалами и неразложимыми инъективными модулями существует соответствие 1–1.

Особенно богатая теория коммутативных нётеровых колец принадлежит Эбену Матлису ( Lam 1999 , §3I). Каждый инъективный модуль однозначно представляет собой прямую сумму неразложимых инъективных модулей, а неразложимые инъективные модули однозначно идентифицируются как инъективные оболочки частных R / P , где P меняется по простому спектру кольца. Инъективная оболочка R / P как R -модуля канонически является RP _- модулем и является RP _- инъективной оболочкой R / P . Другими словами, достаточно рассмотреть локальные кольца . инъективной Кольцо эндоморфизмов оболочки R / P — это пополнение ${\hat {R}}_{P}$ R в P. ^[1]

Двумя примерами являются инъективная оболочка Z -модуля Z / p Z ( группа Прюфера ) и инъективная оболочка k [ x ]-модуля k (кольцо обратных многочленов). Последнее легко описать как k [ x , x ⁻¹]/ хк [ х ]. Этот модуль имеет базис, состоящий из «обратных мономов», то есть x ^{− п} для n = 0, 1, 2, …. Умножение на скаляры происходит так, как и ожидалось, а умножение на x ведет себя нормально, за исключением того, что x · 1 = 0. Кольцо эндоморфизмов — это просто кольцо формальных степенных рядов .

Артиновские примеры

Если G — конечная группа и k — поле с характеристикой 0, то в теории представлений групп показано , что любое подпредставление данного уже является прямым слагаемым данного. В переводе на язык модулей это означает, что все модули над групповой алгеброй kG инъективны. Если характеристика k не равна нулю, может помочь следующий пример.

Если A с единицей — ассоциативная алгебра над полем k с конечной размерностью над k , то Hom _k (−, k ) — двойственность между конечно порожденными левыми A -модулями и конечно порожденными правыми A -модулями. Следовательно, конечно порожденные инъективные левые A -модули — это в точности модули вида Hom _k ( P , k ), где P — конечно порожденный проективный правый A -модуль. Для симметричных алгебр двойственность особенно хорошо проявляется, и проективные и инъективные модули совпадают.

Для любого артинова кольца , как и для коммутативных колец , существует соответствие 1–1 между простыми идеалами и неразложимыми инъективными модулями. Соответствие в этом случае, пожалуй, еще проще: простой идеал — это аннулятор единственного простого модуля, а соответствующий неразложимый инъективный модуль — его инъективная оболочка . Для конечномерных алгебр над полями эти инъективные оболочки являются конечно-порожденными модулями ( Lam 1999 , §3G, §3J).

Вычисление инъективных оболочек

Если $R$ является нётеровым кольцом и ${\mathfrak {p}}$ является простым идеалом, множеством $E=E(R/{\mathfrak {p}})$ как инъективная оболочка. Инъективная оболочка $R/{\mathfrak {p}}$ над Артиновым кольцом $R/{\mathfrak {p}}^{k}$ можно вычислить как модуль $(0:_{E}{\mathfrak {p}}^{k})$ . Это модуль той же длины, что и $R/{\mathfrak {p}}^{k}$ . ^[2] В частности, для стандартного градуированного кольца $R_{\bullet }=k[x_{1},\ldots ,x_{n}]_{\bullet }$ и ${\mathfrak {p}}=(x_{1},\ldots ,x_{n})$ , $E=\oplus _{i}{\text{Hom}}(R_{i},k)$ является инъективным модулем, дающим инструменты для вычисления неразложимых инъективных модулей для артиновых колец над $k$ .

Самоинъективность

Местное кольцо Артина $(R,{\mathfrak {m}},K)$ инъективен сам по себе тогда и только тогда, когда $soc(R)$ представляет собой одномерное векторное пространство над $K$ . Это означает, что каждое локальное горенштейновское кольцо, которое также является артиновым, инъективно само по себе, поскольку имеет одномерный цоколь. ^[3] Простой не пример — кольцо $R=\mathbb {C} [x,y]/(x^{2},xy,y^{2})$ который имеет максимальный идеал $(x,y)$ и поле остатков $\mathbb {C}$ . Его цоколь $\mathbb {C} \cdot x\oplus \mathbb {C} \cdot y$ , который является двумерным. Поле вычетов имеет инъективную оболочку ${\text{Hom}}_{\mathbb {C} }(\mathbb {C} \cdot x\oplus \mathbb {C} \cdot y,\mathbb {C} )$ .

Модули над алгебрами Ли

Для алгебры Ли ${\mathfrak {g}}$ над полем $k$ характеристики 0, категория модулей ${\mathcal {M}}({\mathfrak {g}})$ имеет относительно простое описание своих инъективных модулей. ^[4] Используя универсальную обертывающую алгебру, любая инъективная ${\mathfrak {g}}$ -модуль может быть построен из ${\mathfrak {g}}$ -модуль

${\text{Hom}}_{k}(U({\mathfrak {g}}),V)$

для некоторых $k$ -векторное пространство $V$ . Обратите внимание, что это векторное пространство имеет ${\mathfrak {g}}$ -модульная структура из инъекции

${\mathfrak {g}}\hookrightarrow U({\mathfrak {g}})$

Фактически, каждый ${\mathfrak {g}}$ -модуль имеет инъекцию в некоторые ${\text{Hom}}_{k}(U({\mathfrak {g}}),V)$ и каждое инъективное ${\mathfrak {g}}$ -модуль — это прямое слагаемое некоторого ${\text{Hom}}_{k}(U({\mathfrak {g}}),V)$ .

Теория

Структурная теорема для коммутативных нётеровых колец

Над коммутативным нётеровым кольцом $R$ , каждый инъективный модуль является прямой суммой неразложимых инъективных модулей, а каждый неразложимый инъективный модуль является инъективной оболочкой поля вычетов в простом числе ${\mathfrak {p}}$ . То есть для инъективного $I\in {\text{Mod}}(R)$ , существует изоморфизм

$I\cong \bigoplus _{i}E(R/{\mathfrak {p}}_{i})$

где $E(R/{\mathfrak {p}}_{i})$ – инъективные оболочки модулей $R/{\mathfrak {p}}_{i}$ . ^[5] Кроме того, если $I$ является инъективной оболочкой некоторого модуля $M$ тогда ${\mathfrak {p}}_{i}$ являются ассоциированными простыми числами $M$ . ^[2]

Подмодули, факторы, произведения и суммы, теорема Басса-Паппа.

Любое произведение (даже бесконечного числа) инъективных модулей инъективно; и наоборот, если прямое произведение модулей инъективно, то каждый модуль инъективен ( Lam 1999 , стр. 61). Любая прямая сумма конечного числа инъективных модулей инъективна. В общем, подмодули, фактор-модули или бесконечные прямые суммы инъективных модулей не обязательно должны быть инъективными. Каждый подмодуль каждого инъективного модуля инъективен тогда и только тогда, когда кольцо артиново полупросто ( Golan & Head 1991 , стр. 152); каждый фактор-модуль каждого инъективного модуля инъективен тогда и только тогда, когда кольцо наследственно ( Lam 1999 , Th. 3.22).

Теорема Басса-Паппа утверждает, что каждая бесконечная прямая сумма правых (левых) инъективных модулей инъективна тогда и только тогда, когда кольцо нётерово справа (слева) ( Lam 1999 , стр. 80-81, Th 3.46). ^[6]

критерий Бэра

В оригинальной статье Бэра он доказал полезный результат, обычно известный как критерий Бэра, для проверки инъективности модуля: левый R -модуль Q инъективен тогда и только тогда, когда любой гомоморфизм g : I → Q, определенный на левом идеале I R может быть распространено на все R .

Используя этот критерий, можно показать, что Q — инъективная абелева группа (т. е. инъективный модуль над Z ). В более общем смысле абелева группа инъективна тогда и только тогда, когда она делима . В более общем смысле: модуль над областью главных идеалов инъективен тогда и только тогда, когда он делим (случай векторных пространств является примером этой теоремы, поскольку каждое поле является областью главных идеалов, и каждое векторное пространство является делимым). В случае общей области целостности у нас остается одно следствие: каждый инъективный модуль в области целостности делим.

Критерий Бэра был уточнен многими способами ( Голан и Хед 1991 , стр. 119), включая результат ( Смит 1981 и ( Вамос 1983 ) о том, что для коммутативного нётерова кольца достаточно рассматривать только простые идеалы I. ) Двойственный критерий Бэра, который дает тест на проективность, вообще говоря, ложен. Например, Z -модуль Q удовлетворяет двойственному критерию Бэра, но не является проективным.

Инъекционные когенераторы

Возможно, наиболее важным инъективным модулем является абелева группа Q / Z . Это инъективный когенератор в категории абелевых групп , что означает, что он инъективен и любой другой модуль содержится в достаточно большом произведении копий Q / Z . Так, в частности, каждая абелева группа является подгруппой инъективной. Весьма существенно, что это верно и для любого кольца: каждый модуль является подмодулем инъективного, или «категория левых R -модулей имеет достаточно инъективных». Чтобы доказать это, используются особенности абелевой группы Q / Z для построения инъективного когенератора в категории левых R -модулей.

Для левого R -модуля M так называемый «символьный модуль» M ⁺ = Hom _Z ( M , Q / Z ) — правый R -модуль, который демонстрирует интересную двойственность не между инъективными модулями и проективными модулями , а между инъективными модулями и плоскими модулями ( Enochs & Jenda 2000 , стр. 78–80). Для любого кольца R левый R -модуль плоский тогда и только тогда, когда его характерный модуль инъективен. Если R нетерово слева, то левый R -модуль инъективен тогда и только тогда, когда его характерный модуль плоский.

Инъективные оболочки

Инъективная оболочка модуля — это наименьший инъективный модуль, содержащий данный модуль, который был описан в ( Eckmann & Schopf 1953 ).

Можно использовать инъективные оболочки для определения минимального инъективного разрешения (см. ниже). Если каждый член инъективной резольвенты является инъективной оболочкой коядра предыдущего отображения, то инъективная резольвента имеет минимальную длину.

Инъективные разрешения

Каждый модуль M также имеет инъективную резольвенту : точную последовательность вида

0 → М → Я ⁰ → Я ¹ → Я ² → ...

где я ^дж являются инъективными модулями. Инъективные разрешения можно использовать для определения производных функторов, таких как функтор Ext .

Длина n конечной инъективной резольвенты — это первый индекс такой , что I ^н ненулевое значение, и я ^я = 0 для i больше n . Если модуль M допускает конечную инъективную резольвенту, минимальная длина среди всех конечных инъективных резольвент M называется его инъективной размерностью и обозначается id( M ). Если M не допускает конечной инъективной резольвенты, то по соглашению инъективная размерность называется бесконечной. ( Lam 1999 , §5C) В качестве примера рассмотрим модуль M такой, что id( M ) = 0. В этой ситуации точность последовательности 0 → M → I ⁰ → 0 указывает, что стрелка в центре является изоморфизмом и, следовательно, само M инъективно. ^[7]

Эквивалентно, инъективная размерность M — это минимальное целое число (если оно существует, иначе ∞) n такое, что Ext ^Н
_A (–, M ) = 0 для всех N > n .

Неразложимые

Каждый инъективный подмодуль инъективного модуля является прямым слагаемым, поэтому важно понимать неразложимые инъективные модули ( Lam 1999 , §3F).

Каждый неразложимый инъективный модуль имеет локальное кольцо эндоморфизмов . Модуль называется равномерным, если каждые два ненулевых подмодуля имеют ненулевое пересечение. Для инъективного модуля M следующие условия эквивалентны:

M неразложимо
M ненулевой и является инъективной оболочкой каждого ненулевого подмодуля.
М равномерный
M — инъективная оболочка однородного модуля.
M — инъективная оболочка равномерного циклического модуля.
M имеет локальное кольцо эндоморфизмов

Над нетеровым кольцом каждый инъективный модуль является прямой суммой (единственно определенных) неразложимых инъективных модулей. Над коммутативным нетеровым кольцом это дает особенно хорошее понимание всех инъективных модулей, описанных в ( Matlis 1958 ). Неразложимые инъективные модули — это инъективные оболочки модулей R / p для p — идеал кольца R. простой Более того, инъективная оболочка M группы R / p имеет возрастающую фильтрацию модулями Mn _, заданными аннуляторами идеалов p ^н, а M _{n +1} / M _n изоморфно как конечномерное векторное пространство над полем факторов k ( p ) R / p Hom _{R / p} ( p ^н/ п ^{п +1}, к ( п )).

Смена колец

Важно уметь рассматривать модули над подкольцами или факторкольцами , особенно, например, над полиномиальными кольцами . В общем, это сложно, но известен ряд результатов ( Лам 1999 , стр. 62).

Пусть S и R — кольца, а P — лево- R- , право -S -бимодуль , плоский как лево -R -модуль. Для любого инъективного правого S -модуля M множество гомоморфизмов модулей Hom _S ( P , M ) является инъективным правым R -модулем. То же самое утверждение, конечно, справедливо и после замены левых и правых атрибутов.

Например, если R — подкольцо S такое, что S — плоский R -модуль, то каждый инъективный S -модуль является инъективным R -модулем. В частности, если R — область целостности, а S — ее поле частных , то каждое векторное пространство над S является инъективным R -модулем. Аналогично, каждый инъективный R [ x ]-модуль является инъективным R -модулем.

В обратном направлении кольцевой гомоморфизм $f:S\to R$ превращает R в бимодуль слева- R и справа- S путем левого и правого умножения. Будучи свободным над самим собой, R также является плоским как левый R -модуль. Специализируя приведенное выше утверждение для P = R , оно говорит, что, когда M является инъективным правым S -модулем, коиндуцированный модуль $f_{*}M=\mathrm {Hom} _{S}(R,M)$ является инъективным правым R -модулем. Таким образом, коиндукция по f производит инъективные R -модули из инъективных S -модулей.

Для фактор-колец R / I замена колец также очень очевидна. - модуль R является R / I когда он аннулируется I. -модулем именно тогда , Подмодуль ann _I ( M ) = { m в M : im = 0 для всех i в I } является левым подмодулем левого R -модуля M и является наибольшим подмодулем M , который является R / I -модулем. Если M — инъективный левый R- модуль, то ann _I ( M ) — инъективный левый R / I -модуль. Применяя это к R = Z , I = n Z и M = Q / Z , получаем известный факт, что Z / n Z инъективен как модуль над собой. -модули легко Хотя преобразовать инъективные R -модули в инъективные R / I , этот процесс не преобразует инъективные R -резолюции в инъективные R / I -резолюции, а гомология полученного комплекса является одной из ранних и фундаментальных областей. изучения относительной гомологической алгебры.

В учебнике ( Ротман 1979 , стр. 103) есть ошибочное доказательство того, что локализация сохраняет инъективные формы, но контрпример был дан в ( Дейд 1981 ).

Самоинъекционные кольца

Каждое кольцо с единицей является свободным модулем и, следовательно, проективно как модуль над самим собой, но реже кольцо бывает инъективным как модуль над собой ( Lam 1999 , §3B). Если кольцо инъективно само над собой как правый модуль, то оно называется самоинъективным справа кольцом. Любая алгебра Фробениуса самоинъективна, но никакая область целостности , не являющаяся полем , не является самоинъективной. Каждый собственный фактор дедекиндовой области самоинъективен.

справа Нётерово , самоинъективное справа кольцо называется квазифробениусовым кольцом и является двусторонним артиновым и двусторонним инъективным ( Lam 1999 , Th. 15.1). Важным теоретико-модульным свойством квазифробениусовых колец является то, что проективные модули являются в точности инъективными модулями.

Обобщения и специализации

Инъективные объекты

говорят также Об инъективных объектах в категориях, более общих, чем категории модулей, например, в категориях функторов или в категориях пучков O _X -модулей над некоторым кольцевым пространством ( X ,O _X ). Используется следующее общее определение: объект Q категории C инъективен, если для любого мономорфизма f : X → Y в C и любого морфизма g : X → Q существует морфизм h : Y → Q такой, что hf = g .

Делимые группы

Понятие инъективного объекта в категории абелевых групп изучалось несколько независимо от инъективных модулей под термином делимая группа . Здесь Z -модуль M инъективен тогда и только тогда, когда n ⋅ M = M для любого ненулевого целого числа n . Здесь отношения между плоскими модулями , чистыми подмодулями и инъективными модулями более ясны, поскольку они просто относятся к определенным свойствам делимости элементов модуля целыми числами.

Чистые инъекции

В относительной гомологической алгебре свойство продолжения гомоморфизмов может потребоваться только для некоторых подмодулей, а не для всех. Например, чисто инъективный модуль — это модуль, в котором гомоморфизм чистого подмодуля может быть расширен на весь модуль.

Ссылки

Примечания

^ «Лемма 47.7.5 (08Z6) — Проект Stacks» . stacks.math.columbia.edu . Проверено 25 февраля 2020 г.
^ Jump up to: Перейти обратно: ^а ^б Айзенбуд. Введение в коммутативную алгебру . стр. 624, 625.
^ «Инъективные модули» (PDF) . п. 10.
^ Воган, Дэвид. «Когомологии алгебры Ли» (PDF) .
^ «Структура инъективных модулей над нётеровыми кольцами» .
^ Это теорема Басса -Паппа, см. ( Папп 1959 ) и ( Чейз 1960 )
^ Модуль, изоморфный инъективному модулю, конечно, инъективен.

Учебники

Андерсон, Фрэнк Уайли; Фуллер, Кент Р. (1992), Кольца и категории модулей , Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-0-387-97845-1 , получено 30 июля 2016 г.
Енохс, Эдгар Э.; Дженда, Овертаун М.Г. (2000), Относительная гомологическая алгебра , Изложения де Грюйтера по математике, том. 30, Берлин: Вальтер де Грюйтер и компания, номер документа : 10.1515/9783110803662 , ISBN. 978-3-11-016633-0 , МР 1753146
Голан, Джонатан С.; Хед, Том (1991), Модули и структура колец , Монографии и учебники по чистой и прикладной математике, том. 147, Марсель Деккер, ISBN 978-0-8247-8555-0 , МР 1201818
Лам, Цит-Юэн (1999), Лекции по модулям и кольцам , Тексты для выпускников по математике № 189, Берлин, Нью-Йорк: Springer-Verlag , doi : 10.1007/978-1-4612-0525-8 , ISBN 978-0-387-98428-5 , МР 1653294
Ротман, Джозеф Дж. (1979), Введение в гомологическую алгебру , Чистая и прикладная математика, том. 85, Бостон, Массачусетс: Academic Press , ISBN 978-0-12-599250-3 , МР 0538169

Первоисточники

Баер, Рейнхольд (1940), «Абелевы группы, которые являются прямыми слагаемыми каждой содержащей абелевой группы», Бюллетень Американского математического общества , 46 (10): 800–807, doi : 10.1090/S0002-9904-1940-07306-9 , МР 0002886 , Збл 0024.14902
Чейз, Стивен У. (1960), «Прямое произведение модулей», Труды Американского математического общества , 97 (3), Американское математическое общество, Vol. 97, № 3: 457–473, номер документа : 10.2307/1993382 , JSTOR 1993382 , MR 0120260.
Дейд, Эверетт К. (1981), «Локализация инъективных модулей», Journal of Algebra , 69 (2): 416–425, doi : 10.1016/0021-8693(81)90213-1 , MR 0617087
Экманн, Б .; Шопф, А. (1953), «Об инъективных модулях», Архив математики , 4 (2): 75–78, doi : 10.1007/BF01899665 , MR 0055978
Ламбек, Иоахим (1963), «О кольце частных Утуми» , Canadian Journal of Mathematics , 15 : 363–370, doi : 10.4153/CJM-1963-041-4 , ISSN 0008-414X , MR 0147509
Матлис, Эбен (1958), «Инъективные модули над нетеровыми кольцами», Pacific Journal of Mathematics , 8 : 511–528, doi : 10.2140/pjm.1958.8.511 , ISSN 0030-8730 , MR 0099360
Ософский, Б.Л. (1964), «О кольцевых свойствах инъективных оболочек», Canadian Mathematical Bulletin , 7 : 405–413, doi : 10.4153/CMB-1964-039-3 , ISSN 0008-4395 , MR 0166227
Папп, Золтан (1959), «Об алгебраически замкнутых модулях», Mathematical Publications Debrecen , 6 : 311–327, ISSN 0033-3883 , MR 0121390
Смит, П.Ф. (1981), «Инъективные модули и простые идеалы», Communications in Algebra , 9 (9): 989–999, doi : 10.1080/00927878108822627 , MR 0614468
Утуми, Юзо (1956), «О частных кольцах», Osaka Journal of Mathematics , 8 : 1–18, ISSN 0030-6126 , MR 0078966
Вамос, П. (1983), «Идеалы и модули, проверяющие инъективность», Communications in Algebra , 11 (22): 2495–2505, doi : 10.1080/00927878308822975 , MR 0733337

[1] «Лемма 47.7.5 (08Z6) — Проект Stacks» . stacks.math.columbia.edu . Проверено 25 февраля 2020 г.

[:0-2] Jump up to: Перейти обратно: ^а ^б Айзенбуд. Введение в коммутативную алгебру . стр. 624, 625.

[3] «Инъективные модули» (PDF) . п. 10.

[4] Воган, Дэвид. «Когомологии алгебры Ли» (PDF) .

[5] «Структура инъективных модулей над нётеровыми кольцами» .

[6] Это теорема Басса -Паппа, см. ( Папп 1959 ) и ( Чейз 1960 )

[7] Модуль, изоморфный инъективному модулю, конечно, инъективен.

[1]

[2]

[3]

[4]

[5]

[6]

[7]