Закон Планка

Не путать с соотношением Планка или принципом Планка .

Закон Планка точно описывает излучение черного тела. Здесь показано семейство кривых для разных температур. Классическая (черная) кривая расходится с наблюдаемой интенсивностью на высоких частотах (коротких волнах). Формула в единицах cgs

В физике ( закон Планка также закон излучения Планка) ) описывает спектральную плотность электромагнитного излучения, испускаемого черным телом, находящимся в тепловом равновесии при данной температуре T , когда нет чистого потока вещества или энергии между телом и его средой.

В конце XIX века физики не смогли объяснить, почему наблюдаемый спектр излучения черного тела , который к тому времени был точно измерен, значительно отличался на более высоких частотах от предсказанного существующими теориями. В 1900 году немецкий физик Макс Планк эвристически вывел формулу наблюдаемого спектра, предположив, что гипотетический электрически заряженный осциллятор в полости, содержащей излучение черного тела, может изменять свою энергию только с минимальным приращением E , которое было пропорционально частоте. связанной с ним электромагнитной волны . В то время как Планк первоначально рассматривал гипотезу о разделении энергии на приращения как математическую уловку, введенную просто для получения правильного ответа, другие физики, включая Альберта Эйнштейна, опирались на его работу, и теперь идея Планка признана имеющей фундаментальное значение для квантовой теории .

Закон

Каждое физическое тело самопроизвольно и непрерывно излучает электромагнитное излучение , а спектральное излучение тела B _ν описывает спектральную излучательную мощность на единицу площади, на единицу телесного угла и на единицу частоты для определенных частот излучения. Соотношение закона излучения Планка, приведенное ниже, показывает, что с ростом температуры полная излучаемая энергия тела увеличивается и пик излучаемого спектра смещается в сторону более коротких волн. Согласно закону распределения Планка, спектральная плотность энергии (энергия на единицу объема на единицу частоты) при данной температуре определяется выражением (единицы СИ): $$u_{\nu }(\nu ,T)={\frac {8\pi h\nu ^{3}}{c^{3}}}{\frac {1}{\exp \left({\frac {h\nu }{k_{\mathrm {B} }T}}\right)-1}}$$альтернативно, закон можно выразить для спектральной яркости тела для частоты ν при абсолютной температуре T (в единицах СГС ), заданной как: $$B_{\nu }(\nu ,T)={\frac {2h\nu ^{3}}{c^{2}}}{\frac {1}{\exp \left({\frac {h\nu }{k_{\mathrm {B} }T}}\right)-1}}$$где k _B — постоянная Больцмана , h — постоянная Планка , а c — скорость света в среде, будь то материал или вакуум. Единицами спектральной яркости B _ν в СГС являются эрг · с ⁻¹ · сэр ⁻¹ · см ⁻² · Гц ⁻¹ . Члены B и u связаны друг с другом коэффициентом ⁠ 4π / c ⁠ поскольку B не зависит от направления и излучение распространяется со скоростью c .Спектральная яркость также может быть выражена на единицу длины волны λ вместо единицы частоты. Кроме того, закон может быть выражен и в других терминах, например, в количестве фотонов, испускаемых на определенной длине волны, или в плотности энергии в объеме излучения.

В пределе низких частот (т.е. длинных волн) закон Планка стремится к закону Рэлея-Джинса , а в пределе высоких частот (т.е. малых длин волн) он стремится к приближению Вина .

Макс Планк разработал закон в 1900 году, используя только эмпирически определенные константы, а позже показал, что, выраженный как распределение энергии, это уникальное стабильное распределение излучения в термодинамическом равновесии . Как распределение энергии, это одно из семейства распределений теплового равновесия, которые включают распределение Бозе-Эйнштейна , распределение Ферми-Дирака и распределение Максвелла-Больцмана .

Излучение черного тела

Основная статья: Излучение черного тела

Солнце . приближается к излучателю черного тела Его эффективная температура составляет около 5777 К.

Черное тело — это идеализированный объект, который поглощает и излучает все частоты излучения. Вблизи термодинамического равновесия испускаемое излучение точно описывается законом Планка, и из-за его зависимости от температуры излучение Планка называется тепловым излучением, так что чем выше температура тела, тем больше излучения оно излучает на каждой длине волны.

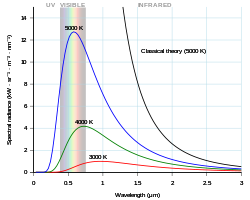
Планковское излучение имеет максимальную интенсивность на длине волны, которая зависит от температуры тела. Например, при комнатной температуре (~ 300 К ) тело излучает тепловое излучение, преимущественно инфракрасное и невидимое. При более высоких температурах количество инфракрасного излучения увеличивается и может ощущаться как тепло, а излучается более видимое излучение, поэтому тело светится заметно красным. При более высоких температурах тело становится ярко-желтым или сине-белым и испускает значительное количество коротковолнового излучения, включая ультрафиолетовые и даже рентгеновские лучи . Поверхность Солнца (~ 6000 К ) излучает большое количество как инфракрасного, так и ультрафиолетового излучения; его излучение достигает максимума в видимом спектре. Этот сдвиг, обусловленный температурой, называется законом смещения Вина .

Планковское излучение — это наибольшее количество излучения, которое любое тело, находящееся в тепловом равновесии, может излучать со своей поверхности, независимо от его химического состава или структуры поверхности. Прохождение излучения через границу раздела сред можно охарактеризовать излучательной способностью границы раздела (отношение фактической яркости к теоретической планковской радиации), обычно обозначаемой символом ε . Обычно он зависит от химического состава и физической структуры, от температуры, длины волны, угла прохождения и поляризации . Коэффициент излучения естественного интерфейса всегда находится в пределах от ε = 0 до 1.

Тело, которое взаимодействует с другой средой, которая имеет ε = 1 и поглощает все падающее на него излучение, называется черным телом. Поверхность черного тела можно смоделировать небольшим отверстием в стене большого помещения, температура которого поддерживается одинаковой, а непрозрачные стены не обладают идеальной отражающей способностью на каждой длине волны. В состоянии равновесия излучение внутри этой оболочки описывается законом Планка, как и излучение, выходящее из маленькой дыры.

Точно так же, как распределение Максвелла-Больцмана является уникальным распределением энергии максимальной энтропии для газа материальных частиц в состоянии теплового равновесия, так же и распределение Планка для газа фотонов . В отличие от материального газа, где массу и количество частиц играют роль, спектральная яркость, давление и плотность энергии фотонного газа при тепловом равновесии полностью определяются температурой.

Если фотонный газ не является планковским, второй закон термодинамики гарантирует, что взаимодействия (между фотонами и другими частицами или даже, при достаточно высоких температурах, между самими фотонами) приведут к изменению распределения энергии фотонов и приближению к планковскому распределению. При таком подходе к термодинамическому равновесию фотоны создаются или уничтожаются в нужном количестве и с нужными энергиями, чтобы заполнить полость с распределением Планка, пока они не достигнут равновесной температуры. Как будто газ представляет собой смесь суб-газов, по одному для каждого диапазона длин волн, и каждый суб-газ в конечном итоге достигает общей температуры.

Величина B _ν ( ν , T ) представляет собой спектральную яркость как функцию температуры и частоты. Его единицы измерения Вт · м. ⁻² · сэр ⁻¹ · Гц ⁻¹ в системе СИ . Бесконечно малая мощность B _ν ( ν , T ) cos θ dA d Ω dν излучается в направлении, описываемом углом θ от нормали к поверхности из бесконечно малой площади поверхности dA в бесконечно малый телесный угол d Ω в бесконечно малой полосе частот шириной dν с центром на частоте ν . Полная мощность, излучаемая в любой телесный угол, представляет собой интеграл от B _ν ( ν , T ) по этим трем величинам и определяется законом Стефана-Больцмана . Спектральная яркость планковского излучения черного тела имеет одно и то же значение для каждого направления и угла поляризации, поэтому черное тело называется ламбертовским излучателем .

Различные формы

Закон Планка можно встретить в нескольких формах в зависимости от соглашений и предпочтений различных научных областей. Различные формы закона спектральной яркости суммированы в таблице ниже. Формы слева чаще всего встречаются в экспериментальных областях , а формы справа чаще всего встречаются в теоретических областях .

Сияние, выраженное через различные спектральные переменные

с ч		с ч
переменная	распределение	переменная	распределение
Частота н	$B_{\nu }(\nu ,T)={\frac {2h\nu ^{3}}{c^{2}}}{\frac {1}{e^{h\nu /(k_{\mathrm {B} }T)}-1}}$	Угловая частота ой	$B_{\omega }(\omega ,T)={\frac {\hbar \omega ^{3}}{4\pi ^{3}c^{2}}}{\frac {1}{e^{\hbar \omega /(k_{\mathrm {B} }T)}-1}}$
Длина волны л	$B_{\lambda }(\lambda ,T)={\frac {2hc^{2}}{\lambda ^{5}}}{\frac {1}{e^{hc/(\lambda k_{\mathrm {B} }T)}-1}}$	Угловая длина волны и	$B_{y}(y,T)={\frac {\hbar c^{2}}{4\pi ^{3}y^{5}}}{\frac {1}{e^{\hbar c/(yk_{\mathrm {B} }T)}-1}}$
Волновое число с	$B_{\tilde {\nu }}({\tilde {\nu }},T)=2hc^{2}{\tilde {\nu }}^{3}{\frac {1}{e^{hc{\tilde {\nu }}/(k_{\mathrm {B} }T)}-1}}$	Угловое волновое число к	$B_{k}(k,T)={\frac {\hbar c^{2}k^{3}}{4\pi ^{3}}}{\frac {1}{e^{\hbar ck/(k_{\mathrm {B} }T)}-1}}$
Дробная полоса пропускания ln х	$B_{\ln x}(x,T)={\frac {2k_{\mathrm {B} }^{4}T^{4}}{h^{3}c^{2}}}{\frac {x^{4}}{e^{x}-1}}$

В формулировке дробной полосы пропускания ${\textstyle x={\frac {h\nu }{k_{\mathrm {B} }T}}={\frac {hc}{\lambda k_{\mathrm {B} }T}}}$, а интегрирование ведется по ${\textstyle \mathrm {d} (\ln x)=\mathrm {d} (\ln \nu )={\frac {\mathrm {d} \nu }{\nu }}=-{\frac {\mathrm {d} \lambda }{\lambda }}=-\mathrm {d} (\ln \lambda )}$.

Закон Планка также можно записать через спектральную плотность энергии ( u ), умножив B на ⁠ 4π / c ⁠ : $$u_{i}(T)={\frac {4\pi }{c}}B_{i}(T).$$

Спектральная плотность энергии, выраженная через различные спектральные переменные

с ч		с ч
переменная	распределение	переменная	распределение
Частота н	$u_{\nu }(\nu ,T)={\frac {8\pi h\nu ^{3}}{c^{3}}}{\frac {1}{e^{h\nu /(k_{\mathrm {B} }T)}-1}}$	Угловая частота ой	$u_{\omega }(\omega ,T)={\frac {\hbar \omega ^{3}}{\pi ^{2}c^{3}}}{\frac {1}{e^{\hbar \omega /(k_{\mathrm {B} }T)}-1}}$
Длина волны л	$u_{\lambda }(\lambda ,T)={\frac {8\pi hc}{\lambda ^{5}}}{\frac {1}{e^{hc/(\lambda k_{\mathrm {B} }T)}-1}}$	Угловая длина волны и	$u_{y}(y,T)={\frac {\hbar c}{\pi ^{2}y^{5}}}{\frac {1}{e^{\hbar c/(yk_{\mathrm {B} }T)}-1}}$
Волновое число с	$u_{\tilde {\nu }}({\tilde {\nu }},T)=8\pi hc{\tilde {\nu }}^{3}{\frac {1}{e^{hc{\tilde {\nu }}/(k_{\mathrm {B} }T)}-1}}$	Угловое волновое число к	$u_{k}(k,T)={\frac {\hbar ck^{3}}{\pi ^{2}}}{\frac {1}{e^{\hbar ck/(k_{\mathrm {B} }T)}-1}}$
Дробная полоса пропускания ln х	$u_{\ln x}(x,T)={\frac {8\pi k_{\mathrm {B} }^{4}T^{4}}{h^{3}c^{3}}}{\frac {x^{4}}{e^{x}-1}}$

Эти распределения представляют спектральную яркость чёрных тел — мощность, излучаемую излучающей поверхностью, на единицу проекции излучающей поверхности, на единицу телесного угла , на единицу спектра (частоту, длину волны, волновое число или их угловые эквиваленты, или дробную частоту или длину волны). . Поскольку излучение изотропно (т.е. не зависит от направления), мощность, излучаемая под углом к ​​нормали , пропорциональна проецируемой площади и, следовательно, косинусу этого угла согласно закону косинуса Ламберта , и неполяризована .

Соответствие форм спектральных переменных

Разные спектральные переменные требуют разных соответствующих форм выражения закона. В общем, нельзя переходить между различными формами закона Планка, просто заменяя одну переменную другой, поскольку при этом не будет учитываться, что разные формы имеют разные единицы измерения. Единицы длины волны и частоты обратны.

Соответствующие формы выражения родственны, поскольку выражают один и тот же физический факт: для определенного физического спектрального приращения излучается соответствующее определенное приращение физической энергии.

Это так, независимо от того, выражается ли это в терминах приращения частоты d ν или, соответственно, длины волны d λ или дробной полосы пропускания d ν / ν или d λ / λ . Введение знака минус может указывать на то, что увеличение частоты соответствует уменьшению длины волны.

Чтобы преобразовать соответствующие формы так, чтобы они выражали одну и ту же величину в одних и тех же единицах, мы умножаем на спектральное приращение. Тогда для конкретного приращения спектра конкретное приращение физической энергии можно записать $$B_{\lambda }(\lambda ,T)\,d\lambda =-B_{\nu }(\nu (\lambda ),T)\,d\nu ,$$что приводит к $$B_{\lambda }(\lambda ,T)=-{\frac {d\nu }{d\lambda }}B_{\nu }(\nu (\lambda ),T).$$

Кроме того, ν ( λ ) = ⁠ c / λ ⁠ , так что ⁠ dν / dλ ⁠ = − ⁠ ц / л ² ⁠ . Подстановка дает соответствие между формами частоты и длины волны с их разными размерностями и единицами измерения. Следовательно, $${\frac {B_{\lambda }(T)}{B_{\nu }(T)}}={\frac {c}{\lambda ^{2}}}={\frac {\nu ^{2}}{c}}.$$

Очевидно, положение максимума спектрального распределения закона Планка зависит от выбора спектральной переменной. Тем не менее, так сказать, эта формула означает, что форма спектрального распределения не зависит от температуры в соответствии с законом смещения Вина, как подробно описано ниже в § Свойства §§ Процентили .

Форма дробной полосы пропускания связана с другими формами соотношением

$B_{\ln x}=\nu B_{\nu }=\lambda B_{\lambda }$.

Первая и вторая константы излучения

В приведенных выше вариантах закона Планка варианты длины волны и волнового числа используют термины 2 hc ² и ⁠ hc / k _B ⁠, которые содержат только физические константы. Следовательно, эти члены сами по себе могут рассматриваться как физические константы. и поэтому называются первой постоянной излучения c _{1 L} и второй постоянной излучения c ₂ с

с _{1 L} = 2 hc ²

и

с ₂ = ⁠ hc / k _B ⁠ .

Используя константы излучения, с длиной волны вариант закона Планка можно упростить до $$L(\lambda ,T)={\frac {c_{1L}}{\lambda ^{5}}}{\frac {1}{\exp \left({\frac {c_{2}}{\lambda T}}\right)-1}}$$и вариант волнового числа может быть упрощен соответственно.

L используется здесь вместо B, потому что это символ SI, обозначающий спектральную яркость . L . в c _{1 L} относится к этому Эта ссылка необходима, потому что закон Планка можно переформулировать, чтобы получить спектральную яркость излучения M ( λ , T ), а не спектральную яркость L ( λ , T ) , и в этом случае c ₁ заменяет c _{1 L} на

c ₁ = 2π hc ² ,

так что закон Планка для спектральной мощности излучения можно записать как $$M(\lambda ,T)={\frac {c_{1}}{\lambda ^{5}}}{\frac {1}{\exp \left({\frac {c_{2}}{\lambda T}}\right)-1}}$$

По мере совершенствования методов измерения Генеральная конференция по мерам и весам пересмотрела свою оценку c ₂ ; см. в Планковском локусе § Международной температурной шкалы подробности .

Физика

Вымораживание генераторов высоких энергий

Закон Планка описывает уникальное и характерное спектральное распределение электромагнитного излучения в термодинамическом равновесии, когда нет чистого потока вещества или энергии. Его физику легче всего понять, рассматривая излучение в полости с жесткими непрозрачными стенками. Движение стен может повлиять на излучение. Если стенки непрозрачны, то термодинамическое равновесие не изолировано. Представляет интерес объяснить, как достигается термодинамическое равновесие. Есть два основных случая: (а) когда термодинамическое равновесие приближается к присутствию материи, когда стенки полости несовершенно отражают для каждой длины волны или когда стенки идеально отражают, в то время как полость содержит небольшое черное тело ( это был основной случай, рассмотренный Планком); или (б) когда приближение к равновесию происходит при отсутствии материи, когда стенки идеально отражают все длины волн, а полость не содержит материи. Для вещества, не заключенного в такую ​​полость, тепловое излучение можно приближенно объяснить соответствующим использованием закона Планка.

Классическая физика с помощью теоремы о равнораспределении привела к ультрафиолетовой катастрофе — предсказанию, что полная интенсивность излучения абсолютно черного тела бесконечна. Если дополнить классически неоправданное предположение о том, что по какой-то причине излучение конечно, классическая термодинамика дает объяснение некоторых аспектов распределения Планка, таких как закон Стефана-Больцмана и закон смещения Вина . В случае присутствия материи квантовая механика дает хорошее объяснение, как показано ниже в разделе, озаглавленном « Коэффициенты Эйнштейна» . Именно этот случай рассматривался Эйнштейном и сегодня используется в квантовой оптике. В случае отсутствия материи необходима квантовая теория поля, поскольку нерелятивистская квантовая механика с фиксированным числом частиц не дает достаточного объяснения.

Фотоны

Квантово-теоретическое объяснение закона Планка рассматривает излучение как газ безмассовых, незаряженных бозонных частиц, а именно фотонов, находящихся в термодинамическом равновесии . Фотоны рассматриваются как переносчики электромагнитного взаимодействия между электрически заряженными элементарными частицами. Число фотонов не сохраняется. Фотоны создаются или уничтожаются в нужном количестве и с нужными энергиями, чтобы заполнить полость с распределением Планка. Для фотонного газа, находящегося в термодинамическом равновесии, плотность внутренней энергии полностью определяется температурой; при этом давление целиком определяется плотностью внутренней энергии. Это отличается от случая термодинамического равновесия для материальных газов, для которых внутренняя энергия определяется не только температурой, но также независимо соответствующими числами различных молекул и, опять же, независимо специфическими характеристиками различных молекул. молекулы. Для разных материальных газов при данной температуре давление и плотность внутренней энергии могут изменяться независимо, поскольку разные молекулы могут независимо переносить разные энергии возбуждения.

Закон Планка возникает как предел распределения Бозе-Эйнштейна , распределения энергии, описывающего неинтерактивные бозоны в термодинамическом равновесии. В случае безмассовых бозонов, таких как фотоны и глюоны , химический потенциал равен нулю, и распределение Бозе-Эйнштейна сводится к распределению Планка. Существует еще одно фундаментальное равновесное распределение энергии: распределение Ферми-Дирака , которое описывает фермионы , такие как электроны, в тепловом равновесии. Эти два распределения различаются, поскольку несколько бозонов могут занимать одно и то же квантовое состояние, а несколько фермионов — нет. При низких плотностях количество доступных квантовых состояний на частицу велико, и эта разница становится несущественной. В пределе низкой плотности распределения Бозе-Эйнштейна и Ферми-Дирака сводятся к распределению Максвелла-Больцмана .

Закон теплового излучения Кирхгофа

Основная статья: Закон теплового излучения Кирхгофа

Закон теплового излучения Кирхгофа представляет собой сжатое и краткое описание сложной физической ситуации. Нижеследующее представляет собой вводный очерк этой ситуации и очень далек от строгого физического аргумента. Целью здесь является лишь суммирование основных физических факторов ситуации и основных выводов.

Спектральная зависимость теплового излучения

Существует разница между кондуктивной теплопередачей и радиационной теплопередачей . Радиационную теплопередачу можно фильтровать так, чтобы она пропускала только определенный диапазон частот излучения.

Общеизвестно, что чем горячее становится тело, тем больше тепла оно излучает на каждой частоте.

В полости непрозрачного тела с жесткими стенками, которые не обладают идеальной отражательной способностью ни на одной частоте, в термодинамическом равновесии существует только одна температура, и она должна быть общей для излучения каждой частоты.

Можно представить себе две такие полости, каждая из которых находится в своем изолированном радиационном и термодинамическом равновесии. Можно представить себе оптическое устройство, обеспечивающее радиационную передачу тепла между двумя полостями, фильтрованную так, чтобы пропускать только определенный диапазон излучательных частот. Если значения спектральной яркости излучений в полостях различаются в этой полосе частот, можно ожидать перехода тепла от более горячего к более холодному. Можно было бы предложить использовать такую ​​фильтрованную передачу тепла в такой полосе для привода тепловой машины. Если два тела имеют одинаковую температуру, второй закон термодинамики не позволяет тепловой машине работать. Можно сделать вывод, что для общей для двух тел температуры значения спектральной яркости в полосе пропускания также должны быть общими. Это должно соблюдаться для каждой полосы частот. Это стало ясно Бальфуру Стюарту, а затем Кирхгофу. Бальфур Стюарт экспериментально обнаружил, что из всех поверхностей одна из ламповой сажи излучает наибольшее количество теплового излучения для каждого качества излучения, судя по различным фильтрам.

Думая теоретически, Кирхгоф пошел немного дальше и указал, что это означает, что спектральная яркость, как функция частоты излучения, любой такой полости в термодинамическом равновесии должна быть уникальной универсальной функцией температуры. Он постулировал идеальное черное тело, которое взаимодействует с окружающей средой таким образом, чтобы поглощать все падающее на него излучение. Согласно принципу взаимности Гельмгольца, излучение изнутри такого тела будет беспрепятственно проходить непосредственно к его окружению, не отражаясь на границе раздела. В термодинамическом равновесии тепловое излучение, испускаемое таким телом, будет иметь уникальное универсальное спектральное излучение в зависимости от температуры. Это понимание лежит в основе закона теплового излучения Кирхгофа.

Связь между поглощательной способностью и излучательной способностью

Можно представить себе небольшое однородное сферическое материальное тело, обозначенное X, при температуре T _X , лежащее в поле излучения внутри большой полости со стенками из материала, обозначенного Y, температуре T _Y. при Тело X излучает собственное тепловое излучение. определенной частоте ν излучение, испускаемое из определенного поперечного сечения через центр X , в каком-то смысле в направлении, нормальном к этому поперечному сечению, может быть обозначено I _{ν , X} ( TX _На ) , что характерно для материала X. . На этой частоте мощность излучения от стенок в это поперечное сечение в противоположном направлении в этом направлении может быть обозначена ν _{, Y (} TY ) _ν , для температуры стенки TY _I . Для материала X , определяя поглощающую способность α _{ν , X , Y} ( TX _TY , ₎ ν долю этого падающего излучения, поглощенного , эта падающая энергия поглощается со скоростью α _{, , X X Y} ( TX _как , Т _Y ) я _{ν , Y} ( Т _Y ) .

Тогда скорость q ( ν , T _X , TY _{накопления энергии в одном} ) смысле в поперечном сечении тела может быть выражена $$q(\nu ,T_{X},T_{Y})=\alpha _{\nu ,X,Y}(T_{X},T_{Y})I_{\nu ,Y}(T_{Y})-I_{\nu ,X}(T_{X}).$$

Основополагающее открытие Кирхгофа, упомянутое выше, заключалось в том, что при термодинамическом равновесии при температуре T существует уникальное универсальное распределение излучения, ныне обозначаемое B _ν ( T ) , которое не зависит от химических характеристик материалов X и Y , что приводит к к очень ценному пониманию равновесия радиационного обмена любого тела вообще, а именно.

Когда существует термодинамическое равновесие при температуре T , излучение полости от стенок имеет то единственное универсальное значение, так что I _{ν , Y} ( TY ₎ = B _ν ( T ) . Далее, можно определить излучательную способность ε _{ν , X} ( T _X ) материала тела X так, чтобы при термодинамическом равновесии при температуре T _X = T было I _{ν , X} ( T _X ) = I _{ν , X} ( Т ) знак равно ε _{ν , Икс} ( Т ) B _ν ( Т ) .

Когда тепловое равновесие преобладает при температуре T = T _X = T _Y , скорость накопления энергии исчезает, так что ( ν , T X _, TY ) _q = 0 . Отсюда следует, что в термодинамическом равновесии T = TX _TY = , _когда , $$0=\alpha _{\nu ,X,Y}(T,T)B_{\nu }(T)-\epsilon _{\nu ,X}(T)B_{\nu }(T).$$

Кирхгоф указал, что из этого следует, что в термодинамическом равновесии T = TX _TY = , _когда , $$\alpha _{\nu ,X,Y}(T,T)=\epsilon _{\nu ,X}(T).$$

Вводя специальные обозначения α _{ν , X} ( T ) для поглощающей способности материала X при термодинамическом равновесии при температуре T (обоснованное открытием Эйнштейна, как указано ниже), получаем далее равенство $$\alpha _{\nu ,X}(T)=\epsilon _{\nu ,X}(T)$$в термодинамическом равновесии.

Продемонстрированное здесь равенство поглощательной способности и излучательной способности характерно для термодинамического равновесия при температуре T и, как правило, не следует ожидать его соблюдения, когда условия термодинамического равновесия не выполняются. Излучательная способность и поглощающая способность являются свойствами молекул материала по отдельности, но они по-разному зависят от распределения состояний молекулярного возбуждения в каждом конкретном случае из-за явления, известного как «вынужденное излучение», которое было открыто Эйнштейном. В тех случаях, когда материал находится в термодинамическом равновесии или в состоянии, известном как локальное термодинамическое равновесие, излучательная способность и поглощающая способность становятся равными. Очень сильное падающее излучение или другие факторы могут нарушить термодинамическое равновесие или локальное термодинамическое равновесие. Локальное термодинамическое равновесие в газе означает, что молекулярные столкновения намного перевешивают излучение и поглощение света при определении распределения состояний молекулярного возбуждения.

Кирхгоф указывал, что он не знает точного характера B _ν ( T ) , но считает важным его выяснить. Спустя четыре десятилетия после открытия Кирхгофом общих принципов его существования и характера, вклад Планка заключался в определении точного математического выражения этого равновесного распределения B _ν ( T ) .

Черное тело

Основная статья: Черное тело

В физике рассматривается идеальное черное тело, обозначенное здесь как B , определяемое как тело, которое полностью поглощает все падающее на него электромагнитное излучение на каждой частоте ν (отсюда и термин «черное»). Согласно закону теплового излучения Кирхгофа это означает, что для каждой частоты ν в термодинамическом равновесии при температуре T имеется α _{ν , B} ( T ) = ε _{ν , B} ( T ) = 1 , так что тепловое излучение от черное тело всегда равно полной величине, определенной законом Планка. Ни одно физическое тело не может излучать тепловое излучение, превышающее тепловое излучение черного тела, поскольку, если бы оно находилось в равновесии с полем излучения, оно излучало бы больше энергии, чем падало на него.

Хотя идеально черных материалов не существует, на практике можно точно аппроксимировать черную поверхность. Что касается материальной внутренней части, то тело из конденсированного вещества, жидкости, твердого тела или плазмы, имеющее определенную границу раздела с окружающей средой, является совершенно черным для излучения, если оно полностью непрозрачно. Это означает, что он поглощает все излучение, проникающее через границу тела с окружающей средой, и попадает в тело. Добиться этого на практике не так уж и сложно. С другой стороны, идеально черного интерфейса в природе не встречается. Идеально черный интерфейс не отражает излучение, а пропускает все, что на него падает, с любой стороны. Лучший практический способ создать эффективно черный интерфейс — это смоделировать «интерфейс» в виде небольшого отверстия в стенке большой полости в полностью непрозрачном твердом теле материала, которое не отражает идеально ни на одной частоте, со стенками, расположенными на одной частоте. контролируемая температура. Помимо этих требований, состав материала стен не ограничен. Излучение, попадающее в отверстие, практически не имеет возможности выйти из полости без поглощения при многократных ударах о ее стенки.

Косинусный закон Ламберта

Основная статья: косинусный закон Ламберта

Как объяснил Планк, Излучающее тело имеет внутреннюю часть, состоящую из материи, и границу раздела с прилегающей к нему соседней материальной средой, которая обычно является средой, изнутри которой наблюдается излучение с поверхности тела. Интерфейс не состоит из физической материи, а представляет собой теоретическую концепцию, математическую двумерную поверхность, совместное свойство двух смежных сред, строго говоря, не принадлежащее ни одной из них по отдельности. Такой интерфейс не может ни поглощать, ни излучать, поскольку не состоит из физической материи; но это место отражения и передачи излучения, поскольку это поверхность разрыва оптических свойств. Отражение и пропускание излучения на границе раздела подчиняются принципу взаимности Стокса–Гельмгольца .

В любой точке недр черного тела, находящегося внутри полости, находящейся в термодинамическом равновесии при температуре Т, излучение однородно, изотропно и неполяризовано. Черное тело поглощает все и не отражает ни одного падающего на него электромагнитного излучения. Согласно принципу взаимности Гельмгольца, излучение изнутри черного тела не отражается от его поверхности, а полностью передается наружу. Из-за изотропности излучения внутри тела спектральная яркость излучения, передаваемого из его внутренней части во внешнюю через его поверхность, не зависит от направления.

Это выражается в том, что излучение поверхности черного тела, находящегося в термодинамическом равновесии, подчиняется закону косинуса Ламберта. Это означает, что спектральный поток d Φ( dA , θ , d Ω, dν ) от заданного бесконечно малого элемента площади dA фактической излучающей поверхности черного тела, обнаруженный с заданного направления, составляющего угол θ с нормалью к фактическая излучающая поверхность в точке dA , в элементе телесного угла обнаружения d Ω с центром в направлении, указанном θ , в элементе полосы частот dν , может быть представлена ​​как $${\frac {d\Phi (dA,\theta ,d\Omega ,d\nu )}{d\Omega }}=L^{0}(dA,d\nu )\,dA\,d\nu \,\cos \theta$$где L ⁰ ( dA , dν ) обозначает поток на единицу площади на единицу частоты на единицу телесного угла, который площадь dA показала бы, если бы она была измерена в нормальном направлении θ = 0 .

Коэффициент cos θ присутствует, поскольку область, к которой непосредственно относится спектральная яркость, представляет собой проекцию фактической площади излучающей поверхности на плоскость, перпендикулярную направлению, указанному θ . Это причина названия косинусного закона .

Учитывая независимость направления спектральной яркости излучения поверхности черного тела, находящегося в термодинамическом равновесии, имеем L ⁰ ( dA , dν ) знак равно B _ν ( T ) и поэтому $${\frac {d\Phi (dA,\theta ,d\Omega ,d\nu )}{d\Omega }}=B_{\nu }(T)\,dA\,d\nu \,\cos \theta .$$

Таким образом, закон косинуса Ламберта выражает независимость направления спектральной яркости B _ν ( T ) поверхности черного тела, находящегося в термодинамическом равновесии.

Закон Стефана – Больцмана

Основная статья: закон Стефана – Больцмана

Полную мощность, излучаемую на единицу площади поверхности черного тела ( P ), можно найти путем интегрирования спектрального потока черного тела, найденного из закона Ламберта, по всем частотам и по телесным углам, соответствующим полусфере ( h ) над поверхностью. . $$P=\int _{0}^{\infty }d\nu \int _{h}d\Omega \,B_{\nu }\cos(\theta )$$

Бесконечно малый телесный угол можно выразить в сферических полярных координатах : $$d\Omega =\sin(\theta )\,d\theta \,d\phi .$$Так что: $$P=\int _{0}^{\infty }d\nu \int _{0}^{\tfrac {\pi }{2}}d\theta \int _{0}^{2\pi }d\phi \,B_{\nu }(T)\cos(\theta )\sin(\theta )=\sigma T^{4}$$где $$\sigma ={\frac {2k_{\mathrm {B} }^{4}\pi ^{5}}{15c^{2}h^{3}}}\approx 5.670400\times 10^{-8}\,\mathrm {J\,s^{-1}m^{-2}K^{-4}}$$ известна как константа Стефана-Больцмана .

Радиационный перенос

Основная статья: Перенос излучения

Уравнение переноса излучения описывает, как влияет излучение при его прохождении через материальную среду. Для частного случая, когда материальная среда находится в термодинамическом равновесии в окрестности точки среды, закон Планка имеет особое значение.

Для простоты можно рассматривать линейное установившееся состояние без рассеяния . Уравнение переноса излучения гласит, что для луча света, проходящего на небольшое расстояние d s , энергия сохраняется: изменение (спектральной) яркости этого луча ( I _ν ) равно количеству, удаленному материальной средой плюс сумма, полученная от материального носителя. Если поле излучения находится в равновесии с материальной средой, эти два вклада будут равны. Материальная среда будет иметь определенный коэффициент излучения и коэффициент поглощения .

Коэффициент поглощения α представляет собой дробное изменение интенсивности светового луча при прохождении расстояния d s и имеет единицы длины. ⁻¹ . Он состоит из двух частей: уменьшения за счет поглощения и увеличения за счет стимулированного излучения . Вынужденное излучение – это излучение материального тела, вызванное и пропорциональное приходящему излучению. Он включен в термин поглощения, поскольку, как и поглощение, он пропорционален интенсивности падающего излучения. Поскольку величина поглощения обычно изменяется линейно пропорционально плотности ρ материала , мы можем определить «коэффициент массового поглощения» κ _ν = ⁠ α / ρ ⁠, которое является свойством самого материала. изменение интенсивности светового луча из-за поглощения при прохождении им небольшого расстояния ds будет равно Тогда $$dI_{\nu }=-\kappa _{\nu }\rho I_{\nu }\,ds$$

«Коэффициент массового излучения» j _ν равен излучению единицы объема элемента малого объема, деленному на его массу (поскольку, что касается массового коэффициента поглощения, излучение пропорционально излучающей массе) и имеет единицы мощности⋅ телесный угол ⁻¹ ⋅frequency ⁻¹ ⋅density ⁻¹ . Как и коэффициент поглощения массы, он также является свойством самого материала. изменение светового луча при прохождении небольшого расстояния ds будет равно Тогда $$dI_{\nu }=j_{\nu }\rho \,ds$$

Тогда уравнение переноса излучения будет суммой этих двух вкладов: $${\frac {dI_{\nu }}{ds}}=j_{\nu }\rho -\kappa _{\nu }\rho I_{\nu }.$$

Если поле излучения находится в равновесии с материальной средой, то излучение будет однородным (независимо от положения), так что dI _ν = 0 и: $$\kappa _{\nu }B_{\nu }=j_{\nu }$$это еще одно утверждение закона Кирхгофа, связывающее два материальных свойства среды и приводящее к уравнению переноса излучения в точке, вокруг которой среда находится в термодинамическом равновесии: $${\frac {dI_{\nu }}{ds}}=\kappa _{\nu }\rho (B_{\nu }-I_{\nu }).$$

Коэффициенты Эйнштейна

Основная статья: Атомная спектральная линия

Принцип детального баланса гласит, что при термодинамическом равновесии каждый элементарный процесс уравновешивается своим обратным процессом.

В 1916 году Альберт Эйнштейн применил этот принцип на атомном уровне к случаю, когда атом излучает и поглощает излучение вследствие переходов между двумя конкретными энергетическими уровнями. давая более глубокое понимание уравнения переноса излучения и закона Кирхгофа для этого типа излучения. Если уровень 1 — это нижний энергетический уровень с энергией E ₁ , а уровень 2 — верхний энергетический уровень с энергией E ₂ , то частота ν излучаемого или поглощаемого излучения будет определяться частотным условием Бора: $$E_{2}-E_{1}=h\nu .$$

Если n ₁ и n ₂ — плотности числа атомов в состояниях 1 и 2 соответственно, то скорость изменения этих плотностей во времени будет обусловлена ​​тремя процессами:

Спонтанное излучение

$\left({\frac {dn_{1}}{dt}}\right)_{\mathrm {spon} }=A_{21}n_{2}$

Вынужденное излучение

$\left({\frac {dn_{1}}{dt}}\right)_{\mathrm {stim} }=B_{21}n_{2}u_{\nu }$

Фотопоглощение

$\left({\frac {dn_{2}}{dt}}\right)_{\mathrm {abs} }=B_{12}n_{1}u_{\nu }$

где u _ν — спектральная плотность энергии поля излучения. Три параметра A ₂₁ , B ₂₁ и B ₁₂ , известные как коэффициенты Эйнштейна, связаны с частотой фотонов ν, образующихся при переходе между двумя энергетическими уровнями (состояниями). В результате каждая линия спектра имеет свой собственный набор связанных коэффициентов. Когда атомы и поле излучения находятся в равновесии, яркость будет определяться законом Планка и, согласно принципу детального баланса, сумма этих скоростей должна быть равна нулю: $$0=A_{21}n_{2}+B_{21}n_{2}{\frac {4\pi }{c}}B_{\nu }(T)-B_{12}n_{1}{\frac {4\pi }{c}}B_{\nu }(T)$$

Поскольку атомы также находятся в равновесии, заселенности двух уровней связаны фактором Больцмана : $${\frac {n_{2}}{n_{1}}}={\frac {g_{2}}{g_{1}}}e^{-h\nu /k_{\mathrm {B} }T}$$где g ₁ и g ₂ — кратности соответствующих энергетических уровней. Объединение двух приведенных выше уравнений с требованием их справедливости при любой температуре дает два соотношения между коэффициентами Эйнштейна: $${\frac {A_{21}}{B_{21}}}={\frac {8\pi h\nu ^{3}}{c^{3}}}$$$${\frac {B_{21}}{B_{12}}}={\frac {g_{1}}{g_{2}}}$$так что знание одного коэффициента даст два других.

В случае изотропного поглощения и излучения коэффициент излучения ( j _ν ) и коэффициент поглощения ( κ _ν ), определенные в разделе о переносе излучения выше, могут быть выражены через коэффициенты Эйнштейна. Соотношения между коэффициентами Эйнштейна дадут выражение закона Кирхгофа, выраженного в разделе «Перенос излучения» выше, а именно: $$j_{\nu }=\kappa _{\nu }B_{\nu }.$$

Эти коэффициенты применимы как к атомам, так и к молекулам.

Характеристики

Пики

Основная статья: Закон смещения Вина

Распределения B _ν , B _ω , B _ν̃ и B _k достигают максимума при энергии фотона $$E=\left[3+W\left(-3e^{-3}\right)\right]k_{\mathrm {B} }T\approx 2.821\ k_{\mathrm {B} }T,$$где W — функция Ламберта W , а e — число Эйлера .

Однако распределение B _λ достигает максимума при другой энергии $$E=\left[5+W\left(-5e^{-5}\right)\right]k_{\mathrm {B} }T\approx 4.965\ k_{\mathrm {B} }T,$$Причина этого в том, что, как упоминалось выше, невозможно перейти от (например) B _ν к B _λ просто заменой ν на λ . Кроме того, нужно еще умножить на ${\textstyle \left|{d\nu }/{d\lambda }\right|=c/{\lambda ^{2}}}$, что смещает пик распределения в сторону более высоких энергий. Эти пики представляют собой энергию моды фотона при группировке с использованием интервалов одинакового размера по частоте или длине волны соответственно. Разделив hc ( 14 387,770 мкм·К ) на это выражение энергии, получим длину волны пика.

Спектральная яркость этих пиков определяется выражением:

${\begin{aligned}B_{\nu ,{\text{max}}}(T)&={\frac {2k_{\mathrm {B} }^{3}T^{3}x^{3}}{h^{2}c^{2}}}{\frac {1}{e^{x}-1}}\\&\approx 1.896\times 10^{-19}{\frac {\mathrm {W} }{\mathrm {m^{2}\cdot Hz\cdot sr} }}\times (T/\mathrm {K} )^{3}\\\end{aligned}}$

с $x=3+W(-3e^{-3}),$ и $${\begin{aligned}B_{\lambda ,{\text{max}}}(T)&={\frac {2k_{\mathrm {B} }^{5}T^{5}x^{5}}{h^{4}c^{3}}}{\frac {1}{e^{x}-1}}\\&\approx 4.096\times 10^{-6}{\frac {\text{W}}{{\text{m}}^{2}\cdot {\text{sr}}}}\times ~(T/{\text{K}})^{5}\end{aligned}}$$с $x=5+W(-5e^{-5}).$

Между тем, средняя энергия фотона абсолютно черного тела равна $$E=\left[{\frac {\pi ^{4}}{30\ \zeta (3)}}\right]k_{\mathrm {B} }T\approx 2.701\ k_{\mathrm {B} }T,$$где $\zeta$ — дзета-функция Римана .

Приближения

Логарифмические графики зависимости яркости от частоты для закона Планка (зеленый) в сравнении с законом Рэлея-Джинса (красный) и приближением Вина (синий) для черного тела при температуре 8 мК .

В пределе низких частот (т.е. длинных волн) закон Планка становится законом Рэлея – Джинса. $$B_{\nu }(T)\approx {\frac {2\nu ^{2}}{c^{2}}}k_{\mathrm {B} }T$$или $$B_{\lambda }(T)\approx {\frac {2c}{\lambda ^{4}}}k_{\mathrm {B} }T$$

Сияние увеличивается пропорционально квадрату частоты, иллюстрируя ультрафиолетовую катастрофу . В пределе высоких частот (т.е. малых длин волн) закон Планка стремится к приближению Вина : $$B_{\nu }(T)\approx {\frac {2h\nu ^{3}}{c^{2}}}e^{-{\frac {h\nu }{k_{\mathrm {B} }T}}}$$ или $$B_{\lambda }(T)\approx {\frac {2hc^{2}}{\lambda ^{5}}}e^{-{\frac {hc}{\lambda k_{\mathrm {B} }T}}}.$$

процентили

процентиль	λ Т (мкм·К)	λ k B T / hc
0.01%	910	0.0632
0.1%	1110	0.0771
1%	1448	0.1006
10%	2195	0.1526
20%	2676	0.1860
25.0%	2898	0.2014
30%	3119	0.2168
40%	3582	0.2490
41.8%	3670	0.2551
50%	4107	0.2855
60%	4745	0.3298
64.6%	5099	0.3544
70%	5590	0.3885
80%	6864	0.4771
90%	9376	0.6517
99%	22884	1.5905
99.9%	51613	3.5873
99.99%	113374	7.8799

Закон смещения Вина в более сильной форме утверждает, что форма закона Планка не зависит от температуры. Поэтому можно перечислить точки процентиля общего излучения, а также пики длины волны и частоты в форме, которая дает длину волны λ , разделенную на температуру T . Во втором столбце следующей таблицы перечислены соответствующие значения λT , то есть те значения x, для которых длина волны λ равна ⁠ x / T ⁠ микрометров в точке процентиля яркости, заданной соответствующей записью в первом столбце.

То есть 0,01% излучения приходится на длину волны ниже ⁠ 910 / Т ⁠ мкм, на 20% ниже ⁠ 2676 / T ⁠ мкм и т. д. Пики длины волны и частоты выделены жирным шрифтом и встречаются при 25,0% и 64,6% соответственно. Точка 41,8% представляет собой нейтральный по длине волны и частоте пик (т.е. пик мощности на единицу изменения логарифма длины волны или частоты). Это точки, в которых действует соответствующий закон Планка. ⁠ 1 / мин ⁵ , н ³ и ⁠ ν ² / л ² ⁠ соответственно, разделенное на exp ( ⁠ hν / k _B T ⁠ ) − 1 достигают максимума. Гораздо меньший разрыв в соотношении длин волн между 0,1% и 0,01% (1110 на 22% больше, чем 910), чем между 99,9% и 99,99% (113374 на 120% больше, чем 51613), отражает экспоненциальный затух энергии на коротких волнах (слева). конец) и полиномиальное затухание в конце.

Какой пик использовать, зависит от приложения. Традиционным выбором является пик длины волны на уровне 25,0%, определяемый законом смещения Вина в его слабой форме. Для некоторых целей более подходящей может оказаться медиана или 50%-ная точка, разделяющая общее излучение на две половины. Последний ближе к пику частоты, чем к пику длины волны, поскольку яркость падает экспоненциально на коротких длинах волн и только полиномиально на длинных. По той же причине нейтральный пик возникает на более короткой длине волны, чем медиана.

Солнечный спектр по сравнению с черным телом при температуре 5775 К.

процентиль	Солнце λ (мкм)	Черное тело на 5778К	288 К планета λ (мкм)
0.01%	0.203	0.157	3.16
0.1%	0.235	0.192	3.85
1%	0.296	0.251	5.03
10%	0.415	0.380	7.62
20%	0.484	0.463	9.29
25.0%	0.520	0.502	10.1
30%	0.556	.540	10.8
41.8%	0.650	0.635	12.7
50%	0.727	0.711	14.3
60%	0.844	0.821	16.5
64.6%	0.911	0.882	17.7
70%	1.003	0.967	19.4
80%	1.242	1.188	23.8
90%	1.666	1.623	32.6
99%	3.728	3.961	79.5
99.9%	8.208	8.933	179
99.99%	17.548	19.620	394

Сравнение с солнечным спектром

Солнечное излучение можно сравнить с излучением черного тела при температуре около 5778 К (но см. график). В таблице справа показано, как распределяется излучение черного тела при этой температуре, а также для сравнения, как распределяется солнечный свет. Также для сравнения показана планета, смоделированная как черное тело, излучающее номинальную температуру 288 К (15 ° C), что является репрезентативным значением сильно меняющейся температуры Земли. Его длины волн более чем в двадцать раз превышают длину волн Солнца, что указано в третьей колонке в микрометрах (тысячах нанометров).

То есть только 1% излучения Солнца приходится на длины волн короче 296 нм и только 1% — на длинах волн более 3728 нм. Если выразить это в микрометрах, то 98% солнечного излучения находится в диапазоне от 0,296 до 3,728 мкм. Соответствующие 98% энергии, излучаемой планетой с температурой 288 К, составляют от 5,03 до 79,5 мкм, что значительно превышает диапазон солнечного излучения (или ниже, если выражать его через частоты ν = ⁠ c / λ ⁠ вместо длин волн λ ).

Следствием этой разницы в длинах волн между солнечным и планетарным излучением, превышающей порядок величины, является то, что фильтры, предназначенные для пропускания одного и блокирования другого, легко построить. Например, окна, изготовленные из обычного стекла или прозрачного пластика, пропускают не менее 80% входящего солнечного излучения с температурой 5778 К, длина волны которого составляет менее 1,2 мкм, и при этом блокируют более 99% исходящего теплового излучения с температурой 288 К от 5 мкм и выше. при котором большинство видов стекла и пластика строительной толщины фактически непрозрачны.

Излучение Солнца – это излучение, достигающее верхних слоев атмосферы (TOA). Как видно из таблицы, излучение с длиной волны ниже 400 нм, или ультрафиолетовое , составляет около 8%, а излучение с длиной волны выше 700 нм, или инфракрасное , начинается примерно с отметки 48% и, таким образом, составляет 52% от общего количества. Следовательно, человеческому глазу видно только 40% инсоляции TOA. Атмосфера существенно сдвигает это процентное соотношение в пользу видимого света, поскольку поглощает большую часть ультрафиолета и значительное количество инфракрасного излучения.

Выводы

Фотонный газ

См. Также: Газ в ящике и фотонный газ.

Рассмотрим куб со стороной L с проводящими стенками, заполненными электромагнитным излучением, находящимся в тепловом равновесии при Т. температуре Если в одной из стен имеется небольшое отверстие, то излучение, испускаемое из отверстия, будет характерно для идеально черного тела . Сначала мы рассчитаем спектральную плотность энергии внутри резонатора, а затем определим спектральную яркость испускаемого излучения.

У стенок куба параллельная составляющая электрического поля и ортогональная составляющая магнитного поля должны исчезнуть. Аналогично волновой функции частицы в ящике можно обнаружить, что поля представляют собой суперпозиции периодических функций. Три длины волны λ ₁ , λ ₂ и λ ₃ в трех направлениях, ортогональных стенкам, могут быть: $$\lambda _{i}={\frac {2L}{n_{i}}},$$где n _i — положительные целые числа. Для каждого набора целых чисел n _i существует два линейно независимых решения (известных как моды). Две моды для каждого набора этих n _i соответствуют двум состояниям поляризации фотона, спин которого равен 1. Согласно квантовой теории, полная энергия моды определяется выражением:

$E_{n_{1},n_{2},n_{3}}\left(r\right)=\left(r+{\frac {1}{2}}\right){\frac {hc}{2L}}{\sqrt {n_{1}^{2}+n_{2}^{2}+n_{3}^{2}}}.$ ( 1 )

Число r можно интерпретировать как количество фотонов в моде. При r = 0 энергия моды не равна нулю. Эта вакуумная энергия электромагнитного поля ответственна за эффект Казимира . Далее мы рассчитаем внутреннюю энергию ящика при абсолютной температуре T .

Согласно статистической механике , равновесное распределение вероятностей по уровням энергии определенного режима определяется выражением: $$P_{r}={\frac {e^{-\beta E\left(r\right)}}{Z\left(\beta \right)}}.$$где мы используем обратную температуру $$\beta \ {\stackrel {\mathrm {def} }{=}}\ {\frac {1}{k_{\mathrm {B} }T}}.$$Знаменатель Z ( β ) является статистической суммой одного режима. Это делает Pr _как правильно нормализованным и может быть оценено $$Z\left(\beta \right)=\sum _{r=0}^{\infty }e^{-\beta E\left(r\right)}={\frac {e^{-\beta \varepsilon /2}}{1-e^{-\beta \varepsilon }}},$$с

$\varepsilon ={\frac {hc}{2L}}{\sqrt {n_{1}^{2}+n_{2}^{2}+n_{3}^{2}}}.$ ( 2 )

это энергия одного фотона. Среднюю энергию в режиме можно получить из статистической суммы : $$\left\langle E\right\rangle =-{\frac {d\log \left(Z\right)}{d\beta }}={\frac {\varepsilon }{2}}+{\frac {\varepsilon }{e^{\beta \varepsilon }-1}}.$$Эта формула, за исключением первого члена энергии вакуума, представляет собой частный случай общей формулы для частиц, подчиняющихся статистике Бозе – Эйнштейна . Поскольку ограничений на общее количество фотонов нет, химический потенциал равен нулю.

Если мы измеряем энергию относительно основного состояния, полная энергия в ящике получается путем суммирования ⟨ E ⟩ - ⁠ ε / 2 ⁠ по всем разрешенным однофотонным состояниям. Это можно сделать точно в термодинамическом пределе, когда L приближается к бесконечности. В этом пределе ε становится непрерывным, и тогда мы можем интегрировать ⟨ E ⟩ − ⁠ ε / 2 ⁠ по этому параметру. Чтобы таким образом вычислить энергию в ящике, нам нужно оценить, сколько состояний фотона существует в данном диапазоне энергий. Если мы запишем общее количество однофотонных состояний с энергиями между ε и ε + dε как g ( ε ) dε , где g ( ε ) — плотность состояний (которая оценивается ниже), то полная энергия будет равна

$U=\int _{0}^{\infty }{\frac {\varepsilon }{e^{\beta \varepsilon }-1}}g(\varepsilon )\,d\varepsilon .$ ( 3 )

Для расчета плотности состояний перепишем уравнение ( 2 ) следующим образом: $$\varepsilon \ {=}\ {\frac {hc}{2L}}n,$$где n - норма вектора n = ( n ₁ , n ₂ , n ₃ ) .

Для каждого вектора n с целочисленными компонентами, большими или равными нулю, существует два состояния фотона. Это означает, что количество фотонных состояний в определенной области n -пространства в два раза превышает объем этой области. Энергетический диапазон dε соответствует оболочке толщиной dn = ⁠ 2 L / hc ⁠ d ε в n -пространстве. Поскольку компоненты n должны быть положительными, эта оболочка охватывает октант сферы. Таким образом, количество фотонных состояний g ( ε ) dε в диапазоне энергий dε определяется выражением: $$g(\varepsilon )\,d\varepsilon =2{\frac {1}{8}}4\pi n^{2}\,dn={\frac {8\pi L^{3}}{h^{3}c^{3}}}\varepsilon ^{2}\,d\varepsilon .$$Подставив это в уравнение ( 3 ) и разделив на объем V = L ³ дает полную плотность энергии $${\frac {U}{V}}=\int _{0}^{\infty }u_{\nu }(T)\,d\nu ,$$где частотно-зависимая спектральная плотность энергии u _ν ( T ) определяется выражением $$u_{\nu }(T)={8\pi h\nu ^{3} \over c^{3}}{1 \over e^{h\nu /k_{\mathrm {B} }T}-1}.$$Поскольку излучение одинаково во всех направлениях и распространяется со скоростью света, спектральная яркость излучения, выходящего из маленького отверстия, равна $$B_{\nu }(T)={\frac {u_{\nu }(T)c}{4\pi }},$$что дает закон Планка $$B_{\nu }(T)={\frac {2h\nu ^{3}}{c^{2}}}~{\frac {1}{e^{h\nu /k_{\mathrm {B} }T}-1}}.$$Другие формы закона можно получить заменой переменных в интеграле полной энергии. Вышеприведенный вывод основан на Brehm & Mullin 1989 .

Дипольное приближение и коэффициенты Эйнштейна

Смотрите также: Коэффициенты Эйнштейна § Дипольное приближение

В невырожденном случае коэффициенты A и B можно рассчитать с использованием дипольного приближения нестационарной теории возмущений в квантовой механике. Вычисление A также требует второго квантования, поскольку полуклассическая теория не может объяснить спонтанное излучение, которое не стремится к нулю, когда возмущающее поле стремится к нулю. Таким образом, рассчитанные скорости перехода составляют (в единицах СИ):

$w_{i\rightarrow f}^{s.emi}={\frac {\omega _{if}^{3}e^{2}}{3\pi \epsilon _{0}\hbar c^{3}}}|\langle f|{\vec {r}}|i\rangle |^{2}=A_{if}$

$w_{i\rightarrow f}^{abs}={\frac {u(\omega _{fi})\pi e^{2}}{3\epsilon _{0}\hbar ^{2}}}|\langle f|{\vec {r}}|i\rangle |^{2}=B_{if}^{abs}u(\omega _{fi})$

$w_{i\rightarrow f}^{emi}={\frac {u(\omega _{if})\pi e^{2}}{3\epsilon _{0}\hbar ^{2}}}|\langle f|{\vec {r}}|i\rangle |^{2}=B_{if}^{emi}u(\omega _{if})$

Обратите внимание, что формула скорости перехода зависит от оператора дипольного момента. Для приближений более высокого порядка он включает квадрупольный момент и другие подобные члены. Таким образом, коэффициенты A и B (которые соответствуют распределению энергии по угловой частоте) равны:

$A_{ab}={\frac {\omega _{ab}^{3}e^{2}}{3\pi \epsilon _{0}\hbar c^{3}}}|\langle a|{\vec {r}}|b\rangle |^{2}$

$B_{ab}={\frac {\pi e^{2}}{3\epsilon _{0}\hbar ^{2}}}|\langle a|{\vec {r}}|b\rangle |^{2}$

где $\omega _{ab}={\frac {E_{a}-E_{b}}{\hbar }}$ а коэффициенты A и B удовлетворяют заданным соотношениям для невырожденного случая:

${\frac {B_{12}}{B_{21}}}=1$ и ${\frac {A_{if}}{B}}={\frac {\omega _{if}^{3}\hbar }{\pi ^{2}c^{3}}}$.

Еще одно полезное соотношение — это соотношение из распределения Максвелла, которое гласит, что количество частиц на энергетическом уровне $E$ пропорциональна показателю $\beta E$. Математически:

${\frac {N_{a}}{N_{b}}}={\frac {e^{-E_{a}\beta }}{e^{-E_{b}\beta }}}=e^{\omega _{ba}\hbar \beta }$

где $N_{a}$ и $N_{b}$ – число занятых энергетических уровней $E_{a}$ и $E_{b}$ соответственно, где $E_{b}>E_{a}$. Затем, используя: ${\frac {dN_{b}}{dt}}=-A_{ba}N_{b}-N_{b}u(\omega _{ba})B_{ba}+N_{a}u(\omega _{ba})B_{ab}=-N_{b}w_{b\rightarrow a}^{s.emi}-N_{b}w_{b\rightarrow a}^{emi}+N_{a}w_{a\rightarrow b}^{abs}$

Решение для $u$ для состояния равновесия ${\frac {dN_{b}}{dt}}=0$, и используя полученные соотношения, получаем Закон Планка:

$u_{\omega }(\omega ,T)={\frac {\omega ^{3}\hbar }{\pi ^{2}c^{3}}}{\frac {1}{e^{\omega \hbar \beta }-1}}$.

История

Бальфур Стюарт

В 1858 году Бальфур Стюарт описал свои эксперименты по изучению излучательной и поглощающей способности полированных пластин из различных веществ по сравнению со способностью черных поверхностей при той же температуре. Стюарт выбрал черные поверхности в качестве эталона из-за различных предыдущих экспериментальных открытий, особенно Пьера Прево и Джона Лесли . Он писал: «Сажа, которая поглощает все падающие на нее лучи и, следовательно, обладает величайшей поглощающей способностью, будет обладать и величайшей возможной излучающей силой».

Стюарт измерял мощность излучения с помощью термобатареи и чувствительного гальванометра, считываемого с помощью микроскопа. Его интересовало избирательное тепловое излучение, которое он исследовал с помощью пластинок веществ, которые излучали и поглощали избирательно для разных качеств излучения, а не максимально для всех качеств излучения. Он обсуждал эксперименты с точки зрения лучей, которые могли отражаться и преломляться и подчинялись принципу взаимности Гельмгольца (хотя он не использовал для него эпоним). В этой статье он не упомянул, что свойства лучей можно описать их длинами волн, и не использовал аппараты спектрального разрешения, такие как призмы или дифракционные решетки. Его работа носила количественный характер в рамках этих ограничений. Он проводил свои измерения при комнатной температуре и быстро, чтобы привести свои тела в состояние, близкое к тепловому равновесию, в котором они были подготовлены путем нагревания до равновесия с кипящей водой. Его измерения подтвердили, что вещества, которые избирательно излучают и поглощают, соблюдают принцип избирательного равенства излучения и поглощения при тепловом равновесии.

Стюарт предложил теоретическое доказательство того, что это должно иметь место отдельно для каждого выбранного качества теплового излучения, но его математические расчеты не были строго верными. По словам историка Д.М. Сигела: «Он не практиковал более сложные методы математической физики девятнадцатого века; он даже не использовал функциональные обозначения при работе со спектральными распределениями». В этой статье он не упомянул термодинамику, хотя и упомянул о сохранении vis viva . Он предположил, что его измерения подразумевают, что излучение поглощается и излучается частицами материи на всей глубине среды, в которой оно распространяется. Он применил принцип взаимности Гельмгольца для объяснения процессов взаимодействия материалов в отличие от процессов во внутреннем материале. Он пришел к выводу, что его эксперименты показали, что внутри помещения, находящегося в тепловом равновесии, лучистое тепло, отраженное и испускаемое вместе, оставляя любую часть поверхности, независимо от ее вещества, было таким же, как если бы оставило ту же самую часть поверхность, если бы она была сделана из ламповой сажи. Он не упомянул о возможности идеально отражающих стен; в частности, он отметил, что хорошо отполированные реальные физические металлы поглощают очень мало.

Густав Кирхгоф

В 1859 году, не зная о работах Стюарта, Густав Роберт Кирхгоф сообщил о совпадении длин волн спектрально разрешенных линий поглощения и излучения видимого света. Что важно для теплофизики, он также заметил, что яркие или темные линии были видны в зависимости от разницы температур между эмиттером и поглотителем.

Кирхгоф продолжил рассматривать тела, излучающие и поглощающие тепловое излучение, находящиеся в непрозрачной оболочке или полости, находящиеся в равновесии при температуре Т. Затем

Здесь использованы обозначения, отличные от Кирхгофа. Здесь мощность излучения E ( T , i ) обозначает размерную величину, полное излучение, испускаемое телом, обозначенным индексом i, при температуре T . Полный коэффициент поглощения a ( T , i ) этого тела безразмерен, это отношение поглощенного к падающему излучению в полости при T. температуре (В отличие от определения Бальфура Стюарта, определение Кирхгофа его коэффициента поглощения не относилось, в частности, к черной поверхности как к источнику падающего излучения.) Таким образом, соотношение ⁠ E ( T , i ) / a ( T , i ) ⁠ отношения излучаемой мощности к поглощению является размерной величиной с размерностями излучающей мощности, поскольку a ( T , i ) безразмерен. Также здесь специфичная для длины волны излучающая способность тела при температуре T обозначается E ( λ , T , i ) , а коэффициент поглощения для конкретной длины волны - a ( λ , T , i ) . И снова соотношение ⁠ E ( λ , T , i ) / a ( λ , T , i ) ⁠ отношения излучаемой мощности к поглощению является размерной величиной, имеющей размеры излучающей мощности.

Во втором отчете, сделанном в 1859 году, Кирхгоф объявил о новом общем принципе или законе, для которого он предложил теоретическое и математическое доказательство, хотя и не предложил количественных измерений мощности излучения. Его теоретическое доказательство было и до сих пор считается некоторыми авторами недействительным. Его принцип, однако, сохранился: он заключался в том, что для тепловых лучей одной и той же длины волны, находящихся в равновесии при данной температуре, отношение излучаемой мощности к коэффициенту поглощения, специфичное для длины волны, имеет одно и то же общее значение для всех тел, которые излучают и поглощать на этой длине волны. В символах закон гласил, что отношение длины волны ⁠ E ( λ , T , i ) / a ( λ , T , i ) ⁠ имеет одно и то же значение для всех тел, то есть для всех значений индекса i . В этом отчете не было упоминания о черных телах.

В 1860 году, еще не зная об измерениях Стюартом некоторых качеств излучения, Кирхгоф указал, что давно экспериментально установлено, что для полного теплового излучения невыбранного качества, испускаемого и поглощаемого телом, находящимся в равновесии, размерный коэффициент полного излучения ⁠ E ( T , i ) / a ( T , i ) ⁠ , имеет одно и то же значение, общее для всех тел, то есть для каждого значения индекса материала i . Опять же, без измерений мощности излучения или других новых экспериментальных данных, Кирхгоф затем предложил новое теоретическое доказательство своего нового принципа универсальности значения отношения длины волны. ⁠ E ( λ , Т , я ) / а ( λ , Т , я ) ⁠ в тепловом равновесии. Его свежее теоретическое доказательство было и до сих пор считается некоторыми авторами недействительным.

Но что еще более важно, он опирался на новый теоретический постулат об «идеально черных телах» , что и является причиной, по которой говорят о законе Кирхгофа. Такие черные тела демонстрировали полное поглощение своей бесконечно тонкой самой поверхностной поверхностью. Они соответствуют телам сравнения Бальфура Стюарта с внутренним излучением, покрытым ламповой сажей. Они не были более реалистичными совершенно черными телами, которые позднее рассматривал Планк. Черные тела Планка излучали и поглощали только материал, находящийся внутри них; их границы с прилегающими средами были лишь математическими поверхностями, не способными ни поглощать, ни излучать, а только отражать и передавать с преломлением.

Доказательство Кирхгофа рассматривало произвольное неидеальное тело с меткой i, а также различные идеальные черные тела с меткой BB . Требовалось, чтобы тела находились в полости в тепловом равновесии при Т. температуре Его доказательство имело целью показать, что соотношение ⁠ E ( λ , T , i ) / a ( λ , T , i ) ⁠ не зависело от природы i неидеального тела, каким бы частично прозрачным или частично отражающим оно ни было.

Его доказательство сначала утверждало, что для длины волны λ и при температуре T , при тепловом равновесии, все совершенно черные тела одного и того же размера и формы имеют одно и то же общее значение излучательной способности E ( λ , T , BB) с размерами власти. В его доказательстве отмечалось, что безразмерный коэффициент поглощения, относящийся к длине волны a ( λ , T , BB ) идеально черного тела, по определению равен точно 1. Тогда для идеально черного тела отношение коэффициента излучения к коэффициенту поглощения, зависящее от длины волны, равно 1. ⁠ E ( λ , T , BB) / a ( λ , T , BB) ⁠ — это снова просто E ( λ , T , BB) с размерностями мощности. Кирхгоф рассматривал последовательно тепловое равновесие с произвольным неидеальным телом и с совершенно черным телом того же размера и формы, находящимся в его полости в равновесии при Т. температуре Он утверждал, что потоки теплового излучения должны быть одинаковыми в каждом случае. Таким образом, он утверждал, что при тепловом равновесии соотношение ⁠ E ( λ , T , i ) / a ( λ , T , i ) ⁠ была равна E ( λ , T , BB) , которую теперь можно обозначить B _λ ( λ , T ) , непрерывную функцию, зависящую только от λ при фиксированной температуре T и возрастающей функции T при фиксированной длине волны λ , при низких температурах исчезающей для видимых, но не для более длинных волн, с положительными значениями для видимых длин волн при более высоких температурах, что не зависит от i природы произвольное неидеальное тело. (Геометрические факторы, подробно учтенные Кирхгофом, здесь не учитывались.)

Таким образом, закон теплового излучения Кирхгофа можно сформулировать : для любого материала, излучающего и поглощающего в термодинамическом равновесии при любой заданной температуре T , для каждой длины волны λ отношение излучательной мощности к коэффициенту поглощения имеет одно универсальное значение, которое характерно для идеально черное тело и является излучающей способностью, которую мы здесь обозначаем B _λ ( λ , T ) . (Для наших обозначений B _λ ( λ , T ) исходное обозначение Кирхгофа было просто e .)

Кирхгоф объявил, что определение функции B _λ ( λ , T ) является задачей первостепенной важности, хотя и признавал, что придется преодолеть экспериментальные трудности. Он предполагал, что, как и другие функции, не зависящие от свойств отдельных тел, это будет простая функция. Эту функцию B _λ ( λ , T ) иногда называли «функцией Кирхгофа (эмиссионной, универсальной)», хотя его точная математическая форма не будет известна еще сорок лет, пока он не будет открыт Планком в 1900 году. Теоретическое доказательство принципа универсальности Кирхгофа разрабатывалось и обсуждалось различными физиками в то же время и позже. Позже, в 1860 году, Кирхгоф заявил, что его теоретическое доказательство было лучше, чем доказательство Бальфура Стюарта, и в некоторых отношениях это было так. В статье Кирхгофа 1860 года не упоминался второй закон термодинамики и, конечно, не упоминалось понятие энтропии, которое в то время еще не было установлено. В более обстоятельном отчете в книге 1862 года Кирхгоф упомянул связь своего закона с «принципом Карно», который является формой второго закона.

По словам Хельге Крага, «квантовая теория обязана своим происхождением изучению теплового излучения, в частности, излучению «черного тела», которое Роберт Кирхгоф впервые определил в 1859–1860 годах».

Эмпирические и теоретические составляющие научной индукции закона Планка.

В 1860 году Кирхгоф предсказал экспериментальные трудности эмпирического определения функции, описывающей зависимость спектра черного тела как функции только от температуры и длины волны. Так и получилось. Чтобы получить достоверный результат, потребовалось около сорока лет разработки усовершенствованных методов измерения электромагнитного излучения.

В 1865 году Джон Тиндалл описал излучение от электрически нагретых нитей и углеродных дуг как видимое и невидимое. Тиндаль спектрально разложил излучение с помощью призмы из каменной соли, которая пропускала как тепло, так и видимые лучи, и измерил интенсивность излучения с помощью термобатареи.

В 1880 году Андре-Проспер-Поль Крова опубликовал диаграмму трехмерного вида графика силы теплового излучения в зависимости от длины волны и температуры. Он определил спектральную переменную с помощью призм. Он анализировал поверхность с помощью так называемых «изотермических» кривых, участков для одной температуры, со спектральной переменной по оси абсцисс и степенной переменной по ординате. Он провел плавные кривые через точки своих экспериментальных данных. Они имели один пик при спектральном значении, характерном для температуры, и падали по обе стороны от него в сторону горизонтальной оси. Такие спектральные участки широко показаны и сегодня.

В серии статей с 1881 по 1886 год Лэнгли сообщил об измерениях спектра теплового излучения с использованием дифракционных решеток и призм и самых чувствительных детекторов, которые он мог изготовить. Он сообщил, что существует пиковая интенсивность, которая увеличивается с температурой, что форма спектра не симметрична относительно пика, что наблюдается сильное падение интенсивности, когда длина волны короче приблизительного порогового значения для каждого при температуре, что приблизительная длина волны отсечки уменьшалась с увеличением температуры и что длина волны пиковой интенсивности уменьшалась с температурой, так что интенсивность сильно возрастала с температурой для коротких длин волн, которые были длиннее, чем приблизительное отсечка для температуры.

Прочитав Лэнгли, русский физик В. А. Майкельсон в 1888 году опубликовал рассмотрение идеи о том, что неизвестная функция излучения Кирхгофа может быть объяснена физически и сформулирована математически в терминах «полной неравномерности колебаний... атомов». В то время Планк не изучал внимательно радиацию и не верил ни в атомы, ни в статистическую физику. Майкельсон вывел формулу спектра температуры: $$I_{\lambda }=B_{1}\theta ^{\frac {3}{2}}\exp \left(-{\frac {c}{\lambda ^{2}\theta }}\right)\lambda ^{-6},$$где I _λ обозначает удельную интенсивность излучения на длине волны λ и температуре θ , и где B ₁ и c являются эмпирическими константами.

В 1898 году Отто Люммер и Фердинанд Курльбаум опубликовали отчет о своем источнике излучения в полости. Их конструкция практически без изменений используется для измерения радиации и по сей день. Это была платиновая коробочка, разделенная диафрагмами, внутренняя часть которой была почернена оксидом железа. Это был важный ингредиент для постепенно совершенствующихся измерений, которые привели к открытию закона Планка. Версия, описанная в 1901 году, имела внутреннюю часть, черненную смесью оксидов хрома, никеля и кобальта.

Важность источника излучения резонатора Люммера и Курльбаума заключалась в том, что он был экспериментально доступным источником излучения черного тела, в отличие от излучения просто экспонированного раскаленного твердого тела, которое было ближайшим доступным экспериментальным приближением к излучению черного тела. подходящий диапазон температур. Просто экспонированные раскаленные твердые тела, которые использовались ранее, излучали излучение с отклонениями от спектра черного тела, что делало невозможным определение истинного спектра черного тела в экспериментах.

Взгляды Планка, прежде чем эмпирические факты, привели его к открытию своего окончательного закона.

Планк впервые обратил внимание на проблему излучения черного тела в 1897 году. Теоретический и эмпирический прогресс позволил Люммеру и Прингсхайму написать в 1899 году, что имеющиеся экспериментальные данные примерно соответствуют закону удельной интенсивности Cλ. ⁻⁵ и ^{− c ⁄ λT} где C и c обозначают эмпирически измеримые константы, а λ и T обозначают длину волны и температуру соответственно. По теоретическим соображениям Планк в то время принял эту формулировку, которая эффективно отсекает короткие волны.

Густав Кирхгоф был учителем Макса Планка и предположил, что существует универсальный закон излучения черного тела, и это было названо «вызовом Кирхгофа». Планк, теоретик, считал, что Вильгельм Вин открыл этот закон, и Планк расширил работу Вина, представив ее в 1899 году на собрании Немецкого физического общества. Экспериментаторы Отто Люммер , Фердинанд Курльбаум , Эрнст Прингсхайм-старший и Генрих Рубенс провели эксперименты, которые, по-видимому, подтвердили закон Вина, особенно на более высоких частотах коротких волн, который Планк настолько полностью поддержал в Немецком физическом обществе, что его стали называть законом Вина-Планка. . Однако к сентябрю 1900 года экспериментаторы вне всякого сомнения доказали, что закон Вина-Планка не работает на более длинных волнах. Они представят свои данные 19 октября. Планку сообщил об этом его друг Рубенс, и он быстро создал формулу в течение нескольких дней. В июне того же года лорд Рэлей создал формулу, которая будет работать для коротких низкочастотных длин волн, основанная на широко распространенной теории равнораспределения . Поэтому Планк представил формулу, сочетающую в себе закон Рэлея (или аналогичную теорию равнораспределения) и закон Вина, которая будет соответствовать тому или иному закону в зависимости от длины волны, чтобы соответствовать экспериментальным данным. Однако, хотя это уравнение работало, сам Планк сказал, что, если он не сможет объяснить формулу, полученную на основе «счастливой интуиции», в формулу «истинного значения» в физике, она не будет иметь истинного значения. Планк объяснил, что после этого последовала самая тяжелая работа в его жизни. Планк не верил в атомы и не считал, что второй закон термодинамики должен быть статистическим, поскольку вероятность не дает абсолютного ответа, а закон энтропии Больцмана основывался на гипотезе атомов и был статистическим. Но Планк не смог найти способ согласовать свое уравнение черного тела с непрерывными законами, такими как волновые уравнения Максвелла. Итак, то, что Планк назвал «актом отчаяния», он обратился к атомному закону энтропии Больцмана, поскольку только он заставил его уравнение работать. Поэтому он использовал постоянную Больцмана k и свою новую константу h для объяснения закона излучения черного тела, который стал широко известен благодаря его опубликованной статье.

Нахождение эмпирического закона

Макс Планк сформулировал свой закон 19 октября 1900 г. как усовершенствование приближения Вина , опубликованного в 1896 году Вильгельмом Вином , которое соответствует экспериментальным данным на коротких длинах волн (высокие частоты), но отклоняется от них на длинных волнах (низкие частоты). В июне 1900 г. на основе эвристических теоретических соображений Рэлей предложил формулу то, что он предложил, можно проверить экспериментально. Было высказано предположение, что универсальная функция Стюарта–Кирхгофа может иметь вид c ₁ Tλ ⁻⁴ exp(– ⁠ c ₂ / λT ⁠ ) . Это не была знаменитая формула Рэлея–Джинса 8π k _B Tλ ⁻⁴ , который появился только в 1905 году, хотя для длинных волн, которые здесь актуальны, оно сводилось к последнему. По словам Кляйна, можно предположить, что Планк, вероятно, видел это предложение, хотя он не упоминал его в своих статьях 1900 и 1901 годов. Планк должен был знать о различных других предложенных формулах. 7 октября 1900 года Рубенс сообщил Планку, что в дополнительной области (длинноволновая, низкая частота) и только там формула Рэлея 1900 года хорошо соответствует наблюдаемым данным.

Для длинных волн эвристическая формула Рэлея 1900 года приблизительно означала, что энергия пропорциональна температуре: U _λ = const. Т. ​ Известно, что ⁠ dS / dU _λ ⁠ = ⁠ 1 / T ⁠ и это приводит к ⁠ dS / dU _λ ⁠ = ⁠ константа. / U _λ ⁠ и оттуда в ⁠ d ² S / dU _λ ² ⁠ = − ⁠ константа. / U _λ ² ⁠ для длинных волн. Но для коротких волн формула Вина приводит к ⁠ 1 / Т ⁠ = − const. ln U _λ + const. и оттуда в ⁠ d ² S / dU _λ ² ⁠ = − ⁠ константа. / U _λ ⁠ для коротких волн. Планк, возможно, объединил эти две эвристические формулы для длинных и коротких волн. вывести формулу $${\frac {d^{2}S}{dU_{\lambda }^{2}}}={\frac {\alpha }{U_{\lambda }(\beta +U_{\lambda })}}.$$

Это привело Планка к формуле $$B_{\lambda }(T)={\frac {C\lambda ^{-5}}{e^{\frac {c}{\lambda T}}-1}},$$где Планк использовал символы C и c для обозначения эмпирических констант аппроксимации.

Планк отправил этот результат Рубенсу, который сравнил его с данными своих наблюдений и Курльбаума и обнаружил, что он удивительно хорошо подходит для всех длин волн. 19 октября 1900 года Рубенс и Курльбаум кратко сообщили о соответствии данным: и Планк добавил короткую презентацию, чтобы дать теоретическое описание своей формулы. В течение недели Рубенс и Курльбаум предоставили более полный отчет о своих измерениях, подтверждающий закон Планка. Их метод спектрального разрешения более длинноволнового излучения назывался методом остаточных лучей. Лучи неоднократно отражались от полированных поверхностей кристаллов, а лучи, прошедшие весь процесс, были «остаточными» и имели длину волны, преимущественно отражаемую кристаллами из подходящего конкретного материала.

Попытка найти физическое объяснение закона

Смотрите также: соотношение Планка

Как только Планк обнаружил эмпирически соответствующую функцию, он построил физический вывод этого закона. Его мысли вращались вокруг энтропии, а не непосредственно вокруг температуры. Планк рассматривал полость с идеально отражающими стенками; внутри полости имеется конечное число различных, но одинаково составленных резонансных колеблющихся тел определенной величины, причем несколько таких осцилляторов на каждой из конечного числа характеристических частот. Эти гипотетические осцилляторы были для Планка чисто воображаемыми теоретическими исследовательскими зондами, и он сказал о них, что такие осцилляторы не обязательно должны «реально существовать где-то в природе, при условии, что их существование и их свойства согласуются с законами термодинамики и электродинамики». Планк не придавал никакого определенного физического значения своей гипотезе резонансных осцилляторов, а скорее предложил ее как математический аппарат, который позволил ему вывести единственное выражение для спектра черного тела, которое соответствовало эмпирическим данным на всех длинах волн. Он предварительно упомянул о возможной связи таких осцилляторов с атомами . В некотором смысле осцилляторы соответствовали углеродной пылинке Планка; размер пятнышка может быть небольшим независимо от размера полости при условии, что пятнышко эффективно преобразует энергию между модами длины волны излучения.

Частично следуя эвристическому методу расчета, впервые разработанному Больцманом для молекул газа, Планк рассмотрел возможные способы распределения электромагнитной энергии по различным режимам своих гипотетических генераторов заряженного материала. Это принятие вероятностного подхода вслед за Больцманом было для Планка радикальным изменением его прежней позиции, которая до этого сознательно выступала против такого мышления, предложенного Больцманом. По словам Планка, «я считал [квантовую гипотезу] чисто формальным предположением и не придавал ей особого значения, за исключением того, что я получил положительный результат при любых обстоятельствах и любой ценой». Эвристически Больцман распределил энергию по произвольным чисто математическим квантам ϵ , которые он начал стремиться к нулю по величине, поскольку конечная величина ϵ служила только для того, чтобы обеспечить возможность точного подсчета ради математического расчета вероятностей, и не имела никакого значения. физическое значение. Говоря о новой универсальной константе природы h , Планк предположил, что в нескольких генераторах каждой из конечного числа характеристических частот полная энергия распределяется по каждому в целом кратном определенной физической единице энергии ϵ , характерной для соответствующей характеристической частоты. Его новая универсальная константа природы h теперь известна как постоянная Планка .

Планк объяснил дальше что соответствующая определенная единица энергии ϵ должна быть пропорциональна соответствующей характеристической частоте колебаний ν гипотетического генератора, и в 1901 году он выразил это с помощью константы пропорциональности h : $$\epsilon =h\nu .$$

Планк не предполагал, что свет, распространяющийся в свободном пространстве, квантуется. Идея квантования свободного электромагнитного поля была развита позже и в конечном итоге включена в то, что мы сейчас знаем как квантовую теорию поля .

В 1906 году Планк признал, что его воображаемые резонаторы, обладающие линейной динамикой, не дают физического объяснения передачи энергии между частотами. Современная физика, следуя Эйнштейну, объясняет преобразование частот в присутствии атомов их квантовой возбудимостью. Планк считал, что в полости с идеально отражающими стенками и без присутствия материи электромагнитное поле не может обмениваться энергией между частотными компонентами. Это происходит из-за линейности уравнений Максвелла . Современная квантовая теория поля предсказывает, что в отсутствие материи электромагнитное поле подчиняется нелинейным уравнениям и в этом смысле взаимодействует с самим собой. Такое взаимодействие в отсутствие материи еще не было измерено напрямую, поскольку оно потребовало бы очень высоких интенсивностей и очень чувствительных и малошумящих детекторов, которые все еще находятся в процессе создания. Планк считал, что поле без взаимодействий не подчиняется и не нарушает классический принцип равнораспределения энергии. и вместо этого остается точно таким, каким оно было при введении, а не превращается в поле черного тела. Таким образом, линейность его механических предположений не позволила Планку найти механическое объяснение максимизации энтропии термодинамически равновесного поля теплового излучения. Вот почему ему пришлось прибегнуть к вероятностным аргументам Больцмана.

Закон Планка можно рассматривать как осуществление предсказания Густава Кирхгофа о том, что его закон теплового излучения имеет важнейшее значение. В своем зрелом изложении своего собственного закона Планк предложил тщательное и подробное теоретическое доказательство закона Кирхгофа: теоретическое доказательство, которое до тех пор иногда обсуждалось, отчасти потому, что оно, как говорили, опиралось на нефизические теоретические объекты, такие как идеально поглощающая бесконечно тонкая черная поверхность Кирхгофа.

Последующие события

Лишь через пять лет после того, как Планк сделал свое эвристическое предположение об абстрактных элементах энергии или действия, Альберт Эйнштейн в 1905 году придумал реально существующие кванты света. как революционное объяснение излучения черного тела, фотолюминесценции, фотоэлектрического эффекта и ионизации газов ультрафиолетовым светом. В 1905 году «Эйнштейн полагал, что теорию Планка невозможно согласовать с идеей квантов света, и эту ошибку он исправил в 1906 году». Вопреки убеждениям Планка того времени, Эйнштейн предложил модель и формулу, согласно которой свет излучается, поглощается и распространяется в свободном пространстве в виде квантов энергии, локализованных в точках пространства. В качестве введения к своим рассуждениям Эйнштейн резюмировал планковскую модель гипотетических резонансных материальных электрических осцилляторов как источников и поглотителей излучения, но затем предложил новый аргумент, не связанный с этой моделью, но частично основанный на термодинамическом аргументе Вина, в котором Планк формула ϵ = hν не играла роли. Эйнштейн дал энергетическое содержание таких квантов в виде ⁠ Рβν / Н ⁠ . Таким образом, Эйнштейн противоречил волновой теории света, которой придерживался Планк. В 1910 году, критикуя рукопись, присланную ему Планком, зная, что Планк был постоянным сторонником специальной теории относительности Эйнштейна, Эйнштейн писал Планку: «Мне кажется абсурдным иметь энергию, непрерывно распределяемую в пространстве, без предположения об эфире».

По словам Томаса Куна , только в 1908 году Планк более или менее принял часть аргументов Эйнштейна в пользу физической дискретности в физике теплового излучения в отличие от абстрактной математической дискретности. Еще в 1908 году, рассматривая предложение Эйнштейна о квантовом распространении, Планк высказал мнение, что такой революционный шаг, возможно, не нужен. До этого Планк был последовательным в своем убеждении, что дискретность квантов действия нельзя обнаружить ни в его резонансных генераторах, ни в распространении теплового излучения. Кун писал, что в более ранних работах Планка и в его монографии 1906 года: нет «упоминания о разрыве, [ни] разговоров об ограничении энергии осциллятора, [ни о] какой-либо формуле типа U = nhν ». Кун отметил, что его исследование статей Планка 1900 и 1901 годов и его монографии 1906 года привели его к «еретическим» выводам, вопреки широко распространенным предположениям других, которые видели сочинения Планка только с точки зрения более поздних, анахроничных точек зрения. Выводы Куна, относящиеся к периоду до 1908 года, когда Планк последовательно придерживался своей «первой теории», были приняты другими историками.

Во втором издании своей монографии в 1912 году Планк поддержал свое несогласие с предложением Эйнштейна о квантах света. Он довольно подробно предположил, что поглощение света его виртуальными материальными резонаторами может быть непрерывным, происходящим с постоянной скоростью в состоянии равновесия, в отличие от квантового поглощения. Только излучение было квантовым. Иногда ее называли «второй теорией» Планка.

Лишь в 1919 году Планк в третьем издании своей монографии более или менее принял свою «третью теорию», согласно которой как излучение, так и поглощение света являются квантовыми.

Яркий термин « ультрафиолетовая катастрофа » был дан Паулем Эренфестом в 1911 году в связи с парадоксальным результатом, заключающимся в том, что полная энергия в полости стремится к бесконечности, когда теорема о равнораспределении классической статистической механики (ошибочно) применяется к излучению черного тела. Но это не входило в мысли Планка, поскольку он не пытался применить доктрину равнораспределения: когда он сделал свое открытие в 1900 году, он не заметил никакой «катастрофы». Впервые это было отмечено лордом Рэлеем в 1900 году. а затем в 1901 году сэр Джеймс Джинс ; и позже, в 1905 году, Эйнштейном, когда он хотел поддержать идею о том, что свет распространяется как дискретные пакеты, позже названные «фотонами», и Рэлеем и Джинс.

В 1913 году Бор дал еще одну формулу с другим физическим смыслом для величины hν . В отличие от формул Планка и Эйнштейна, формула Бора явно и категорически относится к энергетическим уровням атомов. Формула Бора была W _{τ 2} − W _{τ 1} = hν , где W _{τ 2} и W _{τ 1} обозначают энергетические уровни квантовых состояний атома с квантовыми числами τ ₂ и τ ₁ . Символ ν обозначает частоту кванта излучения, который может излучаться или поглощаться при переходе атома между этими двумя квантовыми состояниями. В отличие от модели Планка, частота $\nu$ не имеет непосредственного отношения к частотам, которые могли бы описывать сами эти квантовые состояния.

Позже, в 1924 году, Сатьендра Нат Бозе разработал теорию статистической механики фотонов, которая позволила теоретически вывести закон Планка. Само слово «фотон» было изобретено еще позже, Г. Н. Льюисом в 1926 г. которые ошибочно полагали, что фотоны сохраняются, вопреки статистике Бозе-Эйнштейна; тем не менее слово «фотон» было принято для выражения постулата Эйнштейна о пакетной природе распространения света. В электромагнитном поле, изолированном в вакууме в сосуде с идеально отражающими стенками, как это рассматривал Планк, фотоны действительно сохранялись бы в соответствии с моделью Эйнштейна 1905 года, но Льюис имел в виду поле фотонов, рассматриваемое как система, замкнутая с относительно весомой материи, но открыт для обмена электромагнитной энергией с окружающей системой весомой материи, и он ошибочно полагал, что фотоны все еще сохраняются, сохраняясь внутри атомов.

В конечном итоге закон Планка об излучении черного тела способствовал развитию концепции Эйнштейна о квантах света, несущих линейный импульс. что стало фундаментальной основой развития квантовой механики .

Вышеупомянутая линейность механических предположений Планка, не учитывающая энергетических взаимодействий между частотными компонентами, была заменена в 1925 году оригинальной квантовой механикой Гейзенберга. В своей статье, представленной 29 июля 1925 года, теория Гейзенберга объяснила вышеупомянутую формулу Бора 1913 года. Она признала нелинейные осцилляторы моделями атомных квантовых состояний, допуская энергетическое взаимодействие между их собственными многочисленными внутренними дискретными частотными компонентами Фурье в тех случаях, когда испускания или поглощения квантов излучения. Частота кванта излучения представляла собой частоту определенной связи между внутренними метастабильными колебательными квантовыми состояниями атома. В то время Гейзенберг ничего не знал о матричной алгебре, но Макс Борн прочитал рукопись статьи Гейзенберга и осознал матричный характер теории Гейзенберга. Затем Борн и Джордан опубликовали явно матричную теорию квантовой механики, основанную на оригинальной квантовой механике Гейзенберга, но по форме явно отличающуюся от нее; именно матричная теория Борна и Жордана сегодня называется матричной механикой. Объяснение Гейзенбергом осцилляторов Планка как нелинейных эффектов, проявляющихся как фурье-моды переходных процессов излучения или поглощения излучения, показало, почему осцилляторы Планка, рассматриваемые как устойчивые физические объекты, которые можно было бы представить в классической физике, не дали адекватного объяснения. объяснение явлений.

В настоящее время для описания энергии кванта света часто встречается формула E = ħω , где ħ = ⁠ h / 2π ⁠ , а ω = 2π ν обозначает угловую частоту, и реже эквивалентная формула E = hν . Это утверждение о реально существующем и распространяющемся кванте света, основанное на утверждении Эйнштейна, имеет физический смысл, отличный от приведенного выше утверждения Планка ϵ = hν об абстрактных единицах энергии, которые должны быть распределены среди его гипотетических резонансных материальных осцилляторов.

Статья Хельге Крага, опубликованная в журнале Physics World, дает отчет об этой истории.

См. также

• Коэффициент излучения
• Сияние
• Уравнение Сакумы – Хаттори

Ссылки

Библиография

• Адкинс, CJ (1983). Равновесная термодинамика (3-е изд.). Издательство Кембриджского университета . ISBN  978-0-521-25445-8 .
• Эндрюс, Дэвид (2000). Введение в физику атмосферы . Издательство Кембриджского университета. ISBN  0511800770 .
• Бор, Н. (1913). «О строении атомов и молекул» (PDF) . Философский журнал . 26 (153): 1–25. Бибкод : 1913PMag...26..476B . дои : 10.1080/14786441308634993 .
• Борен, CF ; Клотио, Э.Э. (2006). Основы атмосферной радиации . Вайли-ВЧ . ISBN  978-3-527-40503-9 .
• Больцман, Л. (1878). «О связи между вторым законом механической теории тепла и вероятностным расчетом, соответственно, теоремами о тепловом равновесии». Отчеты о заседании математического и естественнонаучного класса Императорской Академии наук в Вене . 76 (2): 373–435.
• Борн, М .; Вольф, Э. (1999). Принципы оптики (7-е изд.). Издательство Кембриджского университета . ISBN  978-0-521-64222-4 .
• Борн, М .; Джордан, П. (1925). «О квантовой механике». Журнал физики . 34 (1): 858–888. Бибкод : 1925ZPhy...34..858B . дои : 10.1007/BF01328531 . S2CID   186114542 . Частично переведено как «О квантовой механике» в ван дер Варден, БЛ (1967). Источники квантовой механики . Издательство Северной Голландии . стр. 277–306.
• Бозе, Сатьендра Натх (1924). «Закон Планка и квантовая гипотеза света». Журнал физики (на немецком языке). 26 (1): 178–181. Бибкод : 1924ZPhy...26..178B . дои : 10.1007/BF01327326 . S2CID   186235974 .
• Брем, Джей-Джей; Маллин, WJ (1989). Введение в структуру материи . Уайли . ISBN  978-0-471-60531-7 .
• Бриллюэн, Л. (1970). Пересмотр теории относительности . Академическая пресса . ISBN  978-0-12-134945-5 .
• Каниу, Дж. (1999). Пассивное инфракрасное обнаружение: теория и приложения . Спрингер . ISBN  978-0-7923-8532-5 .
• Чандрасекхар, С. (1960) [1950]. Перенос излучения (пересмотренное переиздание). Дуврские публикации . ISBN  978-0-486-60590-6 .
• Коттон, А. (1899). «Современный статус закона Кирхгофа». Астрофизический журнал . 9 : 237–268. Бибкод : 1899ApJ.....9..237C . дои : 10.1086/140585 .
• Крова, АПП (1880). «Исследование излучения, испускаемого раскаленными телами. Оптическое измерение высоких температур» . Анналы химии и физики . Серия 5. 19 : 472–550.
• Дугал, RC (1976). «Изложение формулы излучения Планка (учебное пособие)». Физическое образование . 11 (6): 438–443. Бибкод : 1976PhyEd..11..438D . дои : 10.1088/0031-9120/11/6/008 . S2CID   250881729 .
• Эренфест, П. (1911). «Какие особенности квантовой гипотезы света играют существенную роль в теории теплового излучения?» . Анналы физики . 36 (11): 91–118. Стартовый код : 1911АнП...341...91Э . дои : 10.1002/andp.19113411106 .
• Эренфест, П .; Камерлинг-Оннес, Х. (1914). «Упрощенный вывод формулы из теории комбинаций, которую Планк положил в основу своей теории излучения». Труды Королевской голландской академии наук в Амстердаме . 17 (2): 870–873. Бибкод : 1914KNAB...17..870E .
• Эйнштейн, А. (1905). «Об эвристическом взгляде на образование и преобразование света» . Анналы физики . 17 (6): 132–148. Бибкод : 1905АнП...322..132Е . дои : 10.1002/andp.19053220607 . Переведено на Аронс, AB; Пеппард, МБ (1965). «Предложение Эйнштейна о концепции фотона: перевод статьи Annalen der Physik 1905 года» (PDF) . Американский журнал физики . 33 (5): 367. Бибкод : 1965AmJPh..33..367A . дои : 10.1119/1.1971542 . Архивировано из оригинала (PDF) 4 марта 2016 года . Проверено 19 апреля 2011 г.
• Эйнштейн, А. (1916). «К квантовой теории излучения». Объявления Физического общества Цюриха . 18 :47–62. и почти идентичная версия Эйнштейн, А. (1917). «К квантовой теории излучения». Физический журнал . 18 :121-128. Бибкод : 1917PhyZ...18..121E . Переведено на тер Хаар, Д. (1967). «К квантовой теории излучения» . Старая квантовая теория . Пергамон Пресс . стр. 167–183. LCCN   66029628 . См. также [1] .
• Эйнштейн, А. (1993). Собрание сочинений Альберта Эйнштейна . Том. 3. Английский перевод Бека, издательство А. Принстонского университета . ISBN  978-0-691-10250-4 .
• Фейнман, Р.П .; Лейтон, РБ ; Сэндс, М. (1963). Фейнмановские лекции по физике, том 1 . Аддисон-Уэсли . ISBN  978-0-201-02010-6 .
• Фишер, Т. (1 ноября 2011 г.). «Темы: Вывод закона Планка» . ТермальныйХАБ . Проверено 19 июня 2015 г.
• Гаофэн Шао; Юкао Лу; Дориан А.Х. Ханаор; Шэн Цуй; Цзянь Цзяо; Сяодун Шен (2019). «Повышение стойкости к окислению высокоэмиссионных покрытий на волокнистой керамике для многоразовых космических систем» . Коррозионная наука . 146 . Эльзевир: 233–246. arXiv : 1902.03943 . дои : 10.1016/j.corsci.2018.11.006 . S2CID   118927116 . HAL Id: hal-02308467 – через архивы HAL.
• Гуди, РМ; Юнг, Ю.Л. (1989). Атмосферная радиация: теоретические основы (2-е изд.). Издательство Оксфордского университета . ISBN  978-0-19-510291-8 .
• Гуггенхайм, Э.А. (1967). Термодинамика. Расширенное лечение для химиков и физиков (5-е исправленное изд.). Издательская компания Северной Голландии .
• Хакен, Х. (1981). Свет (Переиздание). Амстердам: Издательство Северной Голландии . ISBN  978-0-444-86020-0 .
• Хапке, Б. (1993). Теория отражения и эмиссионная спектроскопия . Издательство Кембриджского университета , Кембридж, Великобритания. ISBN  978-0-521-30789-5 .
• Гейзенберг, В. (1925). «О квантово-теоретической интерпретации кинематических и механических связей». Журнал физики . 33 (1): 879–893. Бибкод : 1925ZPhy...33..879H . дои : 10.1007/BF01328377 . S2CID   186238950 . Переведено как «Квантово-теоретическая переинтерпретация кинематических и механических отношений» на английском языке. ван дер Варден, БЛ (1967). Источники квантовой механики . Издательство Северной Голландии . стр. 261–276.
• Гейзенберг, В. (1930). Физические основы квантовой теории . Эккарт, К.; Хойт, ФК (перевод). Издательство Чикагского университета .
• Германн, А. (1971). Генезис квантовой теории . Нэш, CW (перевод). МТИ Пресс . ISBN  978-0-262-08047-7 . перевод ранней истории квантовой теории (1899–1913) , Physik Verlag, Мосбах/Баден, 1969.
• Хеттнер, Г. (1922). «Значение работы Рубена для формулы излучения Планка» . естественные науки . 10 (48): 1033–1038. Бибкод : 1922NW.....10.1033H . дои : 10.1007/BF01565205 . S2CID   46268714 .
• Джаммер, М. (1989). Концептуальное развитие квантовой механики (второе изд.). Издательство Томаш / Американский институт физики . ISBN  978-0-88318-617-6 .
• Яух, Дж. М.; Рорлих, Ф. (1980) [1955]. Теория фотонов и электронов. Релятивистская квантовая теория поля заряженных частиц с половинным спином (второе издание второго изд.). Спрингер . ISBN  978-0-387-07295-1 .
• Джинсы, Дж. Х. (1901). «Распределение молекулярной энергии». Философские труды Королевского общества А. 196 (274–286): 397–430. Бибкод : 1901RSPTA.196..397J . дои : 10.1098/rsta.1901.0008 . JSTOR   90811 .
• Джинсы, Дж. Х. (1905а). «XI. О разделении энергии между материей и эфиром» . Философский журнал . 10 (55): 91–98. дои : 10.1080/14786440509463348 .
• Джинсы, Дж. Х. (1905b). «О применении статистической механики к общей динамике материи и эфира» . Труды Королевского общества А. 76 (510): 296–311. Бибкод : 1905RSPSA..76..296J . дои : 10.1098/rspa.1905.0029 . JSTOR   92714 .
• Джинсы, Дж. Х. (1905c). «Сравнение двух теорий радиации» . Природа . 72 (1865): 293–294. Бибкод : 1905Natur..72..293J . дои : 10.1038/072293d0 . S2CID   3955227 .
• Джинсы, Дж. Х. (1905d). «О законах радиации» . Труды Королевского общества А. 76 (513): 545–552. Бибкод : 1905RSPSA..76..545J . дои : 10.1098/rspa.1905.0060 . JSTOR   92704 .
• Джеффрис, Х. (1973). Научный вывод (3-е изд.). Издательство Кембриджского университета . ISBN  978-0-521-08446-8 .
• Кангро, Х. (1976). Ранняя история закона излучения Планка . Тейлор и Фрэнсис . ISBN  978-0-85066-063-0 .
• Карплюс, Р.; Нойман, М. (1951). «Рассеяние света светом». Физический обзор . 83 (4): 776–784. Бибкод : 1951PhRv...83..776K . дои : 10.1103/PhysRev.83.776 .
• Кирхгоф, Г. Р. (1860a). «О линиях Фраунгофера». Ежемесячные отчеты Королевской прусской академии наук в Берлине : 662–665.
• Кирхгоф, Г. Р. (1860b). «О связи между испусканием и поглощением света и тепла». Ежемесячные отчеты Королевской прусской академии наук в Берлине : 783–787.
• Кирхгоф, Г. Р. (1860c). «О связи между излучательной способностью и способностью тел поглощать тепло и свет» . Анналы физики и химии . 109 (2): 275–301. Бибкод : 1860АнП...185..275К . дои : 10.1002/andp.18601850205 . Перевод Гатри Ф. как Кирхгоф, Г. Р. (1860). «О соотношении излучающей и поглощающей способностей различных тел по свету и теплу». Философский журнал . Серия 4. 20 : 1–21.
• Кирхгоф, Г.Р. (1862), «О взаимосвязи между излучательной способностью и способностью тел поглощать тепло и свет», Сборник статей , Иоганн Амброзиус Барт , стр. 571–598.
• Киттель, К. ; Кремер, Х. (1980). Теплофизика (2-е изд.). У. Х. Фриман . ISBN  978-0-7167-1088-2 .
• Кляйн, MJ (1962). «Макс Планк и начало квантовой теории». Архив истории точных наук . 1 (5): 459–479. дои : 10.1007/BF00327765 . S2CID   121189755 .
• Краг, Х. (1999). Квантовые поколения. История физики двадцатого века . Издательство Принстонского университета . ISBN  978-0-691-01206-3 .
• Краг, Х. (декабрь 2000 г.). «Макс Планк: сопротивляющийся революционер» . Мир физики . 13 (12): 31–36. дои : 10.1088/2058-7058/13/12/34 .
• Крамм, Герхард; Мёльдерс, Н. (2009). «Закон излучения черного тела Планка: представление в различных областях и определение соответствующей размерной постоянной». Журнал Калькуттского математического общества . 5 (1–2): 27–61. arXiv : 0901.1863 . Бибкод : 2009arXiv0901.1863K .
• Кун, Т.С. (1978). Теория черного тела и квантовый разрыв . Издательство Оксфордского университета . ISBN  978-0-19-502383-1 .
• Ландсберг, PT (1961). Термодинамика с квантовыми статистическими иллюстрациями . Издательство Интерсайенс .
• Ландсберг, PT (1978). Термодинамика и статистическая механика . Издательство Оксфордского университета . ISBN  978-0-19-851142-7 .
• Льюис, Дж. Н. (1926). «Сохранение фотонов». Природа . 118 (2981): 874–875. Бибкод : 1926Natur.118..874L . дои : 10.1038/118874a0 . S2CID   4110026 .
• Лаудон, Р. (2000). Квантовая теория света (3-е изд.). Издательство Оксфордского университета . ISBN  978-0-19-850177-0 .
• Лоуэн, АН; Бланш, Г. (1940). «Таблицы излучения Планка и фотонных функций». Журнал Оптического общества Америки . 30 (2): 70. Бибкод : 1940JOSA...30...70L . дои : 10.1364/JOSA.30.000070 .
• Ламмер, О. ; Курльбаум, Ф. (1898). «Электрически отожженное «абсолютно черное» тело и измерение его температуры». Переговоры Немецкого физического общества . 17 :106-111.
• Ламмер, О. ; Прингсхайм, Э. (1899). «1. Распределение энергии в спектре черного тела и голой платины; 2. Определение температуры твердых светящихся тел». Переговоры Немецкого физического общества . 1 :215-235.
• Ламмер, О. ; Курльбаум, Ф. (1901). «Электрически отожженное «черное» тело» . Анналы физики . 310 (8): 829–836. Бибкод : 1901АнП...310..829Л . дои : 10.1002/andp.19013100809 .
• Мандель, Л .; Вольф, Э. (1995). Оптическая когерентность и квантовая оптика . Издательство Кембриджского университета . ISBN  978-0-521-41711-2 .
• Мехра, Дж .; Рехенберг, Х. (1982). Историческое развитие квантовой теории . Том. 1. Шпрингер-Верлаг . ISBN  978-0-387-90642-3 .
• Мессия, А. (1958). Квантовая механика . Теммер, Г.Г. (пер.). Уайли .
• Майкельсон, Вирджиния (1888 г.). «Теоретический очерк о распределении энергии в спектрах твердых тел» . Философский журнал . Серия 5. 25 (156): 425–435. дои : 10.1080/14786448808628207 .
• Михалас, Д. ; Вайбель-Михалас, Б. (1984). Основы радиационной гидродинамики . Издательство Оксфордского университета . ISBN  978-0-19-503437-0 .
• Милн, Э.А. (1930). «Термодинамика звезд». Справочник по астрофизике . 3 (1): 63–255.
• Мор, П.Дж.; Тейлор, Б.Н.; Ньюэлл, Д.Б. (2012). «Рекомендуемые CODATA значения фундаментальных физических констант: 2010 г.» (PDF) . Обзоры современной физики . 84 (4): 1527–1605. arXiv : 1203.5425 . Бибкод : 2012РвМП...84.1527М . CiteSeerX   10.1.1.150.1225 . дои : 10.1103/RevModPhys.84.1527 . S2CID   103378639 .
• Палтридж, Джорджия Вирджиния ; Платт, CMR (1976). Радиационные процессы в метеорологии и климатологии . Эльзевир . ISBN  978-0-444-41444-1 .
• Пашен, Ф. (1895). «О законах в спектрах твердых тел и о новом определении температуры Солнца». Новости Королевского общества наук в Геттингене (математическо-физический класс) : 294–304.
• Паули, В. (1973). Энц, CP (ред.). Волновая механика . Маргулис, С.; Льюис, HR (перевод). МТИ Пресс . ISBN  978-0-262-16050-6 .
• Планк, М. (1900а). «Об улучшении спектрального уравнения Вина» . Переговоры Немецкого физического общества . 2 :202-204. Переведено на тер Хаар, Д. (1967). «Об улучшении уравнения Вина для спектра» (PDF) . Старая квантовая теория . Пергамон Пресс . стр. 79–81. LCCN   66029628 .
• Планк, М. (1900b). «К теории закона распределения энергии в нормальном спектре» . Переговоры Немецкого физического общества . 2 :237-245. Переведено на тер Хаар, Д. (1967). «К теории закона распределения энергии нормального спектра» (PDF) . Старая квантовая теория . Пергамон Пресс . п. 82. LCCN   66029628 .
• Планк, М. (1900c). «Энтропия и температура лучистого тепла» . Анналы физики . 306 (4): 719–737. Бибкод : 1900АнП...306..719П . дои : 10.1002/andp.19003060410 .
• Планк, М. (1900d). «О необратимых радиационных процессах» . Анналы физики . 306 (1): 69–122. Стартовый код : 1900АнП...306...69П . дои : 10.1002/andp.19003060105 .
• Планк, М. (1901). «О законе распределения энергии в нормальном спектре» . Анналы физики . 4 (3): 553–563. Стартовый код : 1901АнП...309..553П . дои : 10.1002/andp.19013090310 . Переведено на Андо, К. «О законе распределения энергии в нормальном спектре» (PDF) . Архивировано из оригинала (PDF) 6 октября 2011 года . Проверено 13 октября 2011 г.
• Планк, М. (1906). Лекции по теории теплового излучения . Иоганн Амброзиус Барт . LCCN07004527   .
• Планк, М. (1914). Теория теплового излучения . Перевод Масиуса М. (2-е изд.). Сын П. Блэкистона и компания OL   7154661M .
• Планк, М. (1915). Восемь лекций по теоретической физике, прочитанных в Колумбийском университете в 1909 году (PDF) . Перевод Уиллса, AP Нью-Йорк: издательство Колумбийского университета . Проверено 11 мая 2020 г. - через Project Gutenberg.
• Планк, М. (1943). «К истории открытия физического кванта действия». естественные науки . 31 (14–15): 153–159. Стартовый код : 1943NW.....31..153P . дои : 10.1007/BF01475738 . S2CID   44899488 .
• Рэлей, Лорд (1900). «LIII. Замечания о законе полного излучения» . Философский журнал . Серия 5. 49 (301): 539–540. дои : 10.1080/14786440009463878 .
• Рэлей, Лорд (1905). «Динамическая теория газов и излучения» . Природа . 72 (1855): 54–55. Бибкод : 1905Natur..72...54R . дои : 10.1038/072054c0 . S2CID   4057048 .
• Разавы, М. (2011). Квантовая механика Гейзенберга . Всемирная научная . ISBN  978-981-4304-10-8 .
• Рубенс, Х .; Курльбаум, Ф. (1900а). «Об излучении чёрным телом длинных волн». Переговоры Немецкого физического общества . 2 :181.
• Рубенс, Х .; Курльбаум, Ф. (1900b). «Об испускании длинноволновых тепловых лучей черным телом при различных температурах». Труды Королевской прусской академии наук в Берлине : 929–941. Переведено на Рубенс, Х .; Курльбаум, Ф. (1901). «О тепловом излучении длинных волн, испускаемом черными телами при различных температурах» . Астрофизический журнал . 14 : 335–348. Бибкод : 1901ApJ....14..335R . дои : 10.1086/140874 .
• Рыбицкий, ГБ; Лайтман, AP (1979). Радиационные процессы в астрофизике . Джон Уайли и сыновья . ISBN  978-0-471-82759-7 .
• Шарков, Е.А. (2003). «Излучение черного тела» (PDF) . Пассивное микроволновое дистанционное зондирование Земли . Спрингер . ISBN  978-3-540-43946-2 .
• Шифф, Л.И. (1949). Квантовая механика . МакГроу-Хилл .
• Ширмахер, А. (2001). Экспериментальная теория: доказательства закона излучения Кирхгофа до и после Планка . Мюнхенский центр истории науки и техники .
• Швингер, Дж. (2001). Энглерт, Б.-Г. (ред.). Квантовая механика: символика атомных измерений . Спрингер . ISBN  978-3-540-41408-7 .
• Скалли, Миссури ; Зубайри, М.С. (1997). Квантовая оптика . Издательство Кембриджского университета . ISBN  978-0-521-43458-4 .
• Сигел, DM (1976). «Бальфур Стюарт и Густав Роберт Кирхгоф: два независимых подхода к «закону излучения Кирхгофа» ». Исида . 67 (4): 565–600. дои : 10.1086/351669 . ПМИД   794025 . S2CID   37368520 .
• Сигел, Р .; Хауэлл, младший (2002). Теплопередача теплового излучения, Том 1 (4-е изд.). Тейлор и Фрэнсис . ISBN  978-1-56032-839-1 .
• Зоммерфельд, А. (1923). Атомная структура и спектральные линии . Брозе, HL (перевод) (из 3-го немецкого изд.). Метуэн .
• Стеле, П. (1994). Порядок, Хаос, Порядок. Переход от классической к квантовой физике . Издательство Оксфордского университета . ISBN  978-0-19-507513-7 .
• Стюарт, Б. (1858). «Отчет о некоторых экспериментах по лучистому теплу» . Труды Королевского общества Эдинбурга . 22 : 1–20. дои : 10.1017/S0080456800031288 . S2CID   122316368 .
• тер Хаар, Д. (1967). Старая квантовая теория . Пергамон Пресс . ЛЦН   66-029628 .
• Торнтон, Северная Каролина; Рекс, А.Ф. (2002). Современная физика . Томсон Обучение . ISBN  978-0-03-006049-6 .
• Тиса, Л. (1966). Обобщенная термодинамика . МТИ Пресс .
• Томмазини, Д.; Феррандо, Ф.; Мишинель, Х.; Секо, М. (2008). «Обнаружение фотон-фотонного рассеяния в вакууме на эксаваттных лазерах». Физический обзор А. 77 (1): 042101. arXiv : quant-ph/0703076 . Бибкод : 2008PhRvA..77a2101M . дои : 10.1103/PhysRevA.77.012101 .
• Тиндаль, Дж. (1865a). «О световом и темном излучении» . Анналы физики и химии . 200 (1): 36–53. Нагрудный код : 1865АнП...200...36Т . дои : 10.1002/andp.18652000103 .
• Тиндаль, Дж. (1865b). Теплота рассматривается как способ движения . Д. Эпплтон и компания .
• Вена, В. (1896). «О распределении энергии в спектре излучения черного тела» . Анналы физики и химии . 294 (8): 662–669. Бибкод : 1896АнП...294..662Вт . дои : 10.1002/andp.18962940803 .
• Уилсон, А.Х. (1957). Термодинамика и статистическая механика . Издательство Кембриджского университета .

Внешние ссылки

• Краткое изложение радиации
• Излучение черного тела - интерактивная симуляция игры с законом Планка.
• Статья в Scienceworld о законе Планка