Гиперкубические соты

Обычная квадратная плитка . 1 цвет	Кубические соты правильной формы. 1 цвет
Квадратная плитка в виде шахматной доски 2 цвета	Кубическая сотовая шахматная доска. 2 цвета
Расширенная квадратная плитка 3 цвета	Расширенные кубические соты 4 цвета
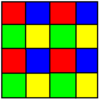4 цвета	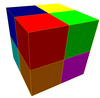8 цветов

В геометрии гиперкубические соты — это семейство правильных сот ( мозаиц ) в $n$ - мерных пространствах с символами Шлефли ${4,3...3,4}$ и содержащее симметрию группы Коксетера $R n$ (или $B ~ n -1$ ) для $n \geq 3$ .

Мозаика строится из 4 $n$ - гиперкубов на гребень . Вершинная фигура представляет собой перекрестный многогранник ${3...3,4}.$

Гиперкубические соты самодвойственны .

Коксетер назвал это семейство $δ n+1,$ что означает $n$ -мерные соты.

Классы конструкции Wythoff по размерам

Конструкция Витгофа — это метод построения однородного многогранника или плоской мозаики.

Двумя основными формами сот гиперкуба являются правильная форма с одинаковыми гиперкубическими гранями и одна полуправильная форма с чередующимися гранями гиперкуба, как шахматная доска .

Третья форма создается в результате операции расширения , примененной к обычной форме, создавая грани вместо всех элементов меньшей размерности. Например, расширенные кубические соты имеют кубические ячейки, центрированные на исходных кубах, на исходных гранях, на исходных краях, на исходных вершинах, создавая ячейки 4 цветов вокруг вершины с шагом 1:3:3:1.

Ортотопические соты представляют собой семейство, топологически эквивалентное кубическим сотам, но с более низкой симметрией, в котором каждое из трех осевых направлений может иметь разную длину ребер. Фасеты представляют собой гиперпрямоугольники , также называемые ортотопами; в 2-х и 3-х измерениях ортотопами являются прямоугольники и кубоиды соответственно.

$δ н$	Имя	Символы Шлефли	Диаграммы Кокстера-Динкина
$δ н$	Имя	Символы Шлефли	Ортотопический ${\infty} (н) (2 м$ цвета, $m < n)$	Обычный ( Расширенный ) ${4,3 п -1,4}$ (1 цвет, $n$ цветов)	шахматная доска ${4,3 н -4,3 1,1}$ (2 цвета)
$д 2$	Апейрогон	${\infty}$
$д 3$	Квадратная плитка	${\infty} (2) {4,4}$
$д 4$	Кубические соты	${\infty} (3) {4,3,4} {4,3 1,1}$
$д 5$	4-кубовые соты	${\infty} (4) {4,3 2,4} {4,3,3 1,1}$
$д 6$	5-кубовые соты	${\infty} (5) {4,3 3,4} {4,3 2,3 1,1}$
$д 7$	6-кубовые соты	${\infty} (6) {4,3 4,4} {4,3 3,3 1,1}$
$д 8$	7-кубовые соты	${\infty} (7) {4,3 5,4} {4,3 4,3 1,1}$
$д 9$	8-кубовые соты	${\infty} (8) {4,3 6,4} {4,3 5,3 1,1}$
$δ н$	$n$ - гиперкубические соты	${\infty} (н) {4,3 n-3,4} {4,3 n-4,3 1,1}$	...

См. также

Ссылки

Коксетер, Правильные многогранники HSM (3-е издание, 1973 г.), Дуврское издание, ISBN 0-486-61480-8
1. стр. 122–123. (Решетка гиперкубов γ _n образует кубические соты , δ _n+1 )
2. стр. 154–156: Частичное усечение или чередование, представленное префиксом h : h{4,4}={4,4}; ч{4,3,4}={3 ^1,1,4}, ч{4,3,3,4}={3,3,4,3}
3. п. 296, Таблица II: Правильные соты, δ _n+1

v т и Основные выпуклые правильные и однородные соты размеров 2–9.
Космос	Семья	${\tilde {A}}_{n-1}$	${\tilde {C}}_{n-1}$	${\tilde {B}}_{n-1}$	${\tilde {D}}_{n-1}$	${\tilde {G}}_{2}$ / ${\tilde {F}}_{4}$ / ${\tilde {E}}_{n-1}$
И ²	Равномерная укладка плитки	{3 ^[3]}	д ₃	HD ₃	квартал ₃	Шестиугольный
И ³	Равномерные выпуклые соты	{3 ^[4]}	д ₄	HD ₄	4 _{квартала}
И ⁴	Униформа 4-сотовая	{3 ^[5]}	д ₅	hδ ₅	qδ ₅	24-ячеистые соты
И ⁵	Униформа 5-сотовая	{3 ^[6]}	д ₆	HD ₆	qδ ₆
И ⁶	Униформа 6-сотовая	{3 ^[7]}	д ₇	hδ ₇	qδ ₇	2 ₂₂
И ⁷	Униформа 7-сотовая	{3 ^[8]}	д ₈	hδ ₈	8 _{кварталов}	1 ₃₃ • 3 ₃₁
И ⁸	Униформа 8-сотовая	{3 ^[9]}	д ₉	HD ₉	qδ ₉	1 ₅₂ • 2 ₅₁ • 5 ₂₁
И ⁹	Униформа 9-сотовая	{3 ^[10]}	д ₁₀	HD ₁₀	10 _{кварталов}
И ¹⁰	Униформа 10-сотовая	{3 ^[11]}	д ₁₁	HD ₁₁	qδ ₁₁
И ^{п -1}	Равномерный ( n -1)- сотовый	{3 ^[н]}	δ _н	hδ _н	qδ _н	1 _{лиц 2} • 2 _{лиц 1} • лиц ₂₁