Квадрик
В математике квадрика или квадрика поверхность ( квадрика гиперповерхность в более высоких измерениях ) является обобщением конических сечений ( эллипсов , парабол и гипербол ). Это гиперповерхность (размерности D ) в ( D + 1) -мерном пространстве, определяемая как нулевое множество второй неприводимого полинома от степени D + 1 переменных; например, D = 1 в случае конических сечений. Когда определяющий многочлен не является абсолютно неприводимым , нулевое множество обычно не считается квадрикой, хотя его часто называют вырожденной квадрикой или приводимой квадрикой .
Таким образом, в координатах x 1 , x 2 , ..., x D +1 общая квадрика определяется алгебраическим уравнением [1]
что можно компактно записать в векторной и матричной записи как:
где x = ( x 1 , x 2 , ..., x D +1 ) строка — вектор- , x Т — транспонирование x , (вектор-столбец), Q — ( D 1) × ( D + 1) матрица P + — ( D + 1) -мерный вектор-строка, а R — скалярная константа. Значения Q , P и R часто считаются действительными или комплексными числами , но квадрика может быть определена для любого поля .
Квадрика — это аффинное алгебраическое многообразие или, если оно приводимо, аффинное алгебраическое множество . Квадрики также могут быть определены в проективных пространствах ; см. § Нормальную форму проективных квадрик ниже.
Евклидова плоскость
[ редактировать ]Поскольку размерность евклидовой плоскости равна двум, квадрики в евклидовой плоскости имеют размерность один и, таким образом, представляют собой плоские кривые . Их называют коническими сечениями , или кониками .

Евклидово пространство
[ редактировать ]В трехмерном евклидовом пространстве квадрики имеют размерность два и известны как квадратичные поверхности . Их квадратные уравнения имеют вид
где являются действительными числами, и по крайней мере одно из A , B и C не равно нулю.
Квадрикические поверхности классифицируются и называются по их форме, которая соответствует орбитам при аффинных преобразованиях . То есть, если аффинное преобразование отображает квадрику на другую, они принадлежат к одному и тому же классу, имеют одно и то же имя и множество свойств.
Теорема о главной оси показывает, что для любой (возможно, приводимой) квадрики подходящая замена декартовых координат или, что то же самое, евклидово преобразование позволяет привести уравнению квадрики к уникальной простой форме, в которой сразу виден класс квадрики. Эта форма называется нормальной формой уравнения, поскольку две квадрики имеют одинаковую нормальную форму тогда и только тогда, когда существует евклидово преобразование, переводящее одну квадрику в другую. Нормальные формы следующие:
где равны 1, –1 или 0, за исключением который принимает только значение 0 или 1.
Каждая из этих 17 нормальных форм [2] соответствует одной орбите при аффинных преобразованиях. В трех случаях реальных точек нет: ( воображаемый эллипсоид ), ( воображаемый эллиптический цилиндр ) и (пара комплексно-сопряженных параллельных плоскостей, приводимая квадрика). В одном случае, воображаемом конусе , имеется единственная точка ( ). Если у одного есть линия (фактически две комплексно-сопряженные пересекающиеся плоскости). Для имеется две пересекающиеся плоскости (приводимая квадрика). Для у одного есть двойной самолет. Для имеется две параллельные плоскости (приводимая квадрика).
Таким образом, среди 17 нормальных форм есть девять истинных квадрик: конус, три цилиндра (часто называемые вырожденными квадриками) и пять невырожденных квадрик ( элллипсоид , параболоид и гиперболоид ), которые подробно описаны в следующих таблицах. Восемь оставшихся квадрик — это воображаемый эллипсоид (без вещественной точки), воображаемый цилиндр (без вещественной точки), воображаемый конус (одна действительная точка) и приводимые квадрики, которые разложены в двух плоскостях; Таких разложенных квадрик пять, в зависимости от того, различны они или нет, параллельны или нет, вещественны или комплексно сопряжены.
| Невырожденные действительные квадратичные поверхности | ||
|---|---|---|
| Эллипсоид | 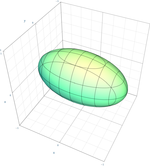 | |
| Эллиптический параболоид | 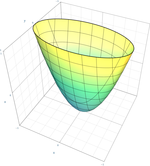 | |
| Гиперболический параболоид |  | |
| Гиперболоид одного листа или Гиперболический гиперболоид | 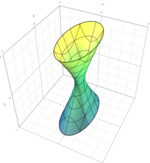 | |
| Гиперболоид из двух листов или Эллиптический гиперболоид | 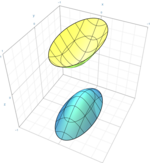 | |
| Вырожденные действительные квадратичные поверхности | ||
|---|---|---|
| Эллиптический конус или Коническая квадрика |  | |
| Эллиптический цилиндр |  | |
| Гиперболический цилиндр | 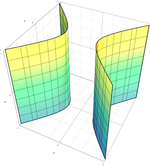 | |
| Параболический цилиндр | 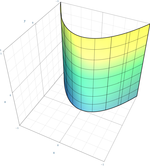 | |
Когда два или более параметров канонического уравнения равны, получается квадрика вращения , которая остается инвариантной при вращении вокруг оси (или бесконечного числа осей, в случае сферы).
| Квадрики революции | ||
|---|---|---|
| Сплющенные и вытянутые сфероиды (частные случаи эллипсоида) |   | |
| Сфера (частный случай сфероида) |  | |
| Круговой параболоид (частный случай эллиптического параболоида) |  | |
| Гиперболоид вращения одного листа (частный случай гиперболоида одного листа) |  | |
| Гиперболоид вращения двух листов (частный случай двухлистного гиперболоида) | 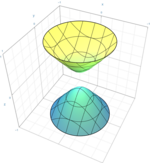 | |
| Круглый конус (частный случай эллиптического конуса) | 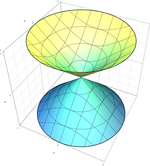 | |
| Круглый цилиндр (частный случай эллиптического цилиндра) |  | |
Определение и основные свойства
[ редактировать ]Аффинная квадрика — это множество нулей многочлена второй степени. Если не указано иное, предполагается, что полином имеет действительные коэффициенты, а нули — это точки в евклидовом пространстве . Однако большинство свойств остаются верными, когда коэффициенты принадлежат любому полю , а точки принадлежат аффинному пространству . Как обычно в алгебраической геометрии , часто бывает полезно рассматривать точки над алгебраически замкнутым полем, содержащим полиномиальные коэффициенты, обычно комплексные числа , когда коэффициенты действительны.
Многие свойства становится легче сформулировать (и доказать) путем расширения квадрики до проективного пространства посредством проективного завершения , состоящего из добавления точек на бесконечности . Технически, если
является многочленом второй степени, определяющим аффинную квадрику, то его проективное пополнение определяется путем усреднения p в
(это полином, поскольку степень p равна двум). Точками проективного пополнения являются точки проективного пространства, проективные координаты которых являются нулями P .
Итак, проективная квадрика — это множество нулей в проективном пространстве однородного многочлена второй степени.
Поскольку описанный выше процесс гомогенизации можно обратить вспять, установив X 0 = 1 :
часто бывает полезно не отличать аффинную квадрику от ее проективного пополнения и говорить об аффинном уравнении или проективном уравнении квадрики. Однако это не полная эквивалентность; это вообще тот случай, что будет включать точки с , которые не являются также решениями потому что эти точки в проективном пространстве соответствуют точкам «на бесконечности» в аффинном пространстве.
Уравнение
[ редактировать ]Квадрика в аффинном пространстве размерности n — это множество нулей многочлена степени 2. То есть это множество точек, координаты которых удовлетворяют уравнению
где многочлен p имеет вид
для матрицы с и работает от 0 до . Когда характеристика поля , коэффициентов не равна двум, как правило предполагается; эквивалентно . Когда характеристика поля коэффициентов равна двум, как правило, предполагается, когда ; эквивалентно имеет верхнюю треугольную форму .
Уравнение можно сократить, так как матричное уравнение
с
Уравнение проективного пополнения практически идентично:
с
уравнения определяют квадрику как алгебраическую гиперповерхность размерности Эти n – 1 и степени два в пространстве размерности n .
Квадрика называется невырожденной, если матрица является обратимым .
Невырожденная квадрика неособа в том смысле, что ее проективное пополнение не имеет особой точки (цилиндр неособ в аффинном пространстве, но это вырожденная квадрика, имеющая особую точку на бесконечности).
Особыми точками вырожденной квадрики являются точки, проективные координаты которых принадлежат нулевому пространству матрицы A .
Квадрика приводима тогда и только тогда, когда ранг A равен единице (случай двойной гиперплоскости) или двум (случай двух гиперплоскостей).
Нормальная форма проективных квадрик
[ редактировать ]В реальном проективном пространстве , согласно закону инерции Сильвестра , неособая квадратичная форма P ( X ) может быть приведена в нормальную форму
с помощью подходящего проективного преобразования (нормальные формы сингулярных квадрик могут иметь как нули, так и ±1 в качестве коэффициентов). Для двумерных поверхностей (размерность D = 2) в трехмерном пространстве существует ровно три невырожденных случая:
Первый случай — пустое множество.
Второй случай порождает эллипсоид, эллиптический параболоид или двухлистный гиперболоид в зависимости от того, разрезает ли выбранная плоскость на бесконечности квадрику в пустом множестве, в точке или в невырожденной конике соответственно. Все они имеют положительную гауссову кривизну .
Третий случай порождает гиперболический параболоид или однолистный гиперболоид в зависимости от того, разрезает ли плоскость на бесконечности две прямые или невырожденную конику соответственно. Это двулинейчатые поверхности отрицательной гауссовой кривизны.
Вырожденная форма
генерирует эллиптический цилиндр, параболический цилиндр, гиперболический цилиндр или конус, в зависимости от того, пересекает ли плоскость на бесконечности его точку, линию, две прямые или невырожденную конику соответственно. Это однолинейчатые поверхности нулевой гауссовой кривизны.
Мы видим, что проективные преобразования не смешивают гауссовы кривизны разных знаков. Это справедливо для поверхностей общего назначения. [3]
В комплексном проективном пространстве все невырожденные квадрики становятся неотличимы друг от друга.
Рациональная параметризация
[ редактировать ]Для неособой точки А квадрики прямая, проходящая через А, либо касается квадрики, либо пересекает квадрику ровно в одной другой точке (как обычно, прямая, содержащаяся в квадрике, считается касательной, так как она содержится в касательной гиперплоскости ). Это означает, что прямые, проходящие через А и не касающиеся квадрики, находятся во взаимно однозначном соответствии с точками квадрики, не принадлежащими касательной гиперплоскости в А. точке Выражение точек квадрики через направление соответствующей прямой дает параметрические уравнения следующего вида.
В случае конических сечений (квадричных кривых) эта параметризация устанавливает биекцию между проективным коническим сечением и проективной прямой ; эта биекция является изоморфизмом алгебраических кривых . В более высоких размерностях параметризация определяет бирациональное отображение , которое представляет собой биекцию между плотными открытыми подмножествами квадрики и проективным пространством той же размерности (рассматриваемая топология является обычной в случае вещественной или комплексной квадрики, или топология Зарисского во всех случаях). являются точками пересечения квадрики и ее касательной гиперплоскости в точке A. Точки квадрики, не входящие в образ этой биекции ,
В аффинном случае параметризация представляет собой рациональную параметризацию вида
где – координаты точки квадрики, являются параметрами, а являются полиномами степени не выше двух.
В проективном случае параметризация имеет вид
где – проективные координаты точки квадрики, являются параметрами, а являются однородными многочленами второй степени.
От одной параметризации к другой можно перейти, полагая и
Для вычисления параметризации и доказательства того, что степени соответствуют заявленным, в аффинном случае можно поступить следующим образом. Аналогично можно поступить и в проективном случае.
Пусть q — квадратичный многочлен, определяющий квадрику, и — координатный вектор данной точки квадрики (так, Позволять - координатный вектор точки квадрики, подлежащей параметризации, и — вектор, определяющий направление, используемое для параметризации (здесь не учитываются направления, последняя координата которых равна нулю; это означает, что некоторые точки аффинной квадрики не параметризуются; часто говорят, что они параметризуются точками, находящимися на бесконечности в пространство параметров). Точки пересечения квадрики и линии направления проходя через точки такой, что
для некоторого значения скаляра Это уравнение второй степени за исключением значений такая, что прямая касается квадрики (при этом степень равна единице, если прямая не входит в квадрику, или уравнение принимает вид в противном случае). Коэффициенты и имеют соответственно степень не более первой и второй в Поскольку постоянный коэффициент уравнение становится линейным при делении на и его единственным решением является частное многочлена степени не выше одной на многочлен степени не выше двух. Подставив это решение в выражение получаем искомую параметризацию в виде дробей многочленов степени не выше двух.
Пример: круг и сферы.
[ редактировать ]Рассмотрим квадрику уравнения
Для это единичный круг ; для это единичная сфера ; в более высоких измерениях это единичная гиперсфера .
Суть принадлежит квадрике (выбор этой точки среди других подобных точек является лишь вопросом удобства). Итак, уравнение предыдущего раздела становится
Расширяя квадраты, упрощая постоянные члены, деля на и решение в получается
Подставив это в и упрощая выражение последней координаты, получаем параметрическое уравнение
Путем гомогенизации получаем проективную параметризацию
Непосредственная проверка показывает, что это индуцирует биекцию между точками квадрики такую, что и точки такие, что в проективном пространстве параметров. С другой стороны, все значения такой, что и дать точку
В случае конических сечений ( ), существует ровно одна точка с и между окружностью и проективной прямой имеется биекция.
Для есть много моментов с и, следовательно, множество значений параметров для точки С другой стороны, остальные точки квадрики, для которых (и таким образом ) невозможно получить ни при каком значении параметров. Эти точки являются точками пересечения квадрики и ее касательной плоскости в точке В данном конкретном случае эти точки имеют невещественные комплексные координаты, но достаточно изменить один знак в уравнении квадрики, чтобы получить вещественные точки, которые не получаются при результирующей параметризации.
Рациональные точки
[ редактировать ]Квадрика над полем определяется если коэффициенты его уравнения принадлежат Когда это поле Из рациональных чисел можно предположить, что коэффициенты являются целыми , очистив знаменатели .
Точка квадрики, определенной над полем считается рациональным если его координаты принадлежат Рациональная точка над полем действительных чисел называется действительной точкой.
Рациональная точка зрения называется просто рациональной точкой . Очистив знаменатели, можно предположить и вообще предполагается, что проективные координаты рациональной точки (в квадрике, определенной над ) являются целыми числами. Кроме того, очищая знаменатели коэффициентов, обычно предполагается, что все коэффициенты уравнения квадрики и полиномы, встречающиеся при параметризации, являются целыми числами.
Таким образом, нахождение рациональных точек проективной квадрики равносильно решению диофантова уравнения .
Учитывая рациональную точку A над квадрикой над полем F , параметризация, описанная в предыдущем разделе, обеспечивает рациональные точки, когда параметры находятся в F , и, наоборот, каждая рациональная точка квадрики может быть получена из параметров в F , если точка не находится в касательной гиперплоскости в A. точке
Отсюда следует, что если квадрика имеет рациональную точку, у нее есть много других рациональных точек (бесконечно много, если F бесконечно), и эти точки могут быть сгенерированы алгоритмически, как только будет известна одна из них.
Как сказано выше, в случае проективных квадрик, определенных над параметризация принимает вид
где — однородные многочлены второй степени с целыми коэффициентами. Из-за однородности можно рассматривать только параметры, которые являются взаимно простыми целыми числами. Если — уравнение квадрики, решение этого уравнения называется примитивным, если его компоненты являются взаимно простыми целыми числами. Примитивные решения находятся во взаимно однозначном соответствии с рациональными точками квадрики ( с точностью до смены знака всех компонент решения). Непримитивные целочисленные решения получаются путем умножения примитивных решений на произвольные целые числа; поэтому они не заслуживают специального изучения. Однако взаимно простые параметры могут давать непримитивные решения, и, возможно, придется разделить на наибольший общий делитель, чтобы получить соответствующее примитивное решение.
Пифагоровы тройки
[ редактировать ]Это хорошо иллюстрируют пифагоровы тройки . Тройка Пифагора – это тройка. натуральных чисел таких, что Тройка Пифагора примитивна , если взаимно просты или, что то же самое, если какая-либо из трех пар и является взаимно простым.
Выбрав описанный выше метод обеспечивает параметризацию
для квадрики уравнения (Имена переменных и параметров меняются с приведенных выше на те, которые распространены при рассмотрении троек Пифагора).
Если m и n — взаимно простые целые числа такие, что полученная тройка является тройкой Пифагора. Если один из m и n четный, а другой нечетный, полученная тройка является примитивной; в противном случае m и n оба нечетны, и путем деления на 2 получается примитивная тройка.
Таким образом, примитивные пифагорейские тройки с даже получаются как
с m и n взаимно простыми целыми числами, одно из которых четное и (это формула Евклида ). Примитивные пифагорейские тройки с нечетные получаются как
с m и n взаимно простыми нечетными целыми числами такими, что
Поскольку замена a и b превращает одну пифагорову тройку в другую пифагорову тройку, только одного из двух случаев достаточно для создания всех примитивных пифагоровых троек.
Проективные квадрики над полями
[ редактировать ]Определение проективной квадрики в вещественном проективном пространстве (см. выше) можно формально адаптировать, определив проективную квадрику в n -мерном проективном пространстве над полем . Чтобы не иметь дело с координатами, проективная квадрика обычно определяется, начиная с квадратичной формы в векторном пространстве. [4]
Квадратичная форма
[ редактировать ]Позволять быть полем и векторное пространство над . Отображение от к такой, что
- (1 квартал) для любого и .
- (2 квартал) представляет собой билинейную форму .
называется квадратичной формой . Билинейная форма является симметричным .
В случае билинейная форма , то есть и взаимно определяются уникальным образом.
В случае (это означает: ) билинейная форма обладает свойством , то есть является симплектический .
Для и ( является основой ) имеет знакомую форму
- и
- .
Например:
n -мерное проективное пространство над полем
[ редактировать ]Позволять быть полем, ,
- an ( n + 1) — размерное векторное пространство над полем
- одномерное подпространство, порожденное ,
- набор точек ,
- набор линий .
- — n -мерное проективное пространство над .
- Множество точек, содержащихся в -мерное подпространство это -мерное подпространство . Двумерное подпространство — это плоскость .
- В случае а -мерное подпространство называется гиперплоскостью .
Проективная квадрика
[ редактировать ]Квадратичная форма в векторном пространстве определяет квадрику в связанном проективном пространстве как набор точек такой, что . То есть,
Примеры в .:
(E1): Для получается коника .
(E2): Для получается пара линий с уравнениями и , соответственно. Они пересекаются в точке ;
Для дальнейших рассуждений предполагается, что .
Полярное пространство
[ редактировать ]Для точки набор
называется полярным пространством (по отношению к ).
Если для всех , получается .
Если хотя бы для одного , уравнение — нетривиальное линейное уравнение, определяющее гиперплоскость. Следовательно
- является либо гиперплоскостью , либо .
Пересечение с линией
[ редактировать ]Для пересечения произвольной прямой с квадрикой , могут возникнуть следующие случаи:
- а) и называется внешней линией
- б) и называется прямой в квадрике
- в) и называется касательной
- г) и называется секущей линией .
Доказательство: Позволять быть линией, которая пересекает в точку и это второй пункт .От получается
И) В случае уравнение держится и это для любого . Следовательно, либо для любого или для любого , что доказывает б) и б').
II) В случае получается и уравнение имеет ровно одно решение .Следовательно: , что доказывает в).
Кроме того, доказательство показывает:
- линия через точку является касательной тогда и только тогда, когда .
f -радикал, q -радикал
[ редактировать ]В классических случаях или существует только один радикал, поскольку и и тесно связаны. В случае квадрика не определяется (см. выше), поэтому приходится иметь дело с двумя радикалами:
- а) является проективным подпространством. называется f -радикалом квадрики .
- б) называется сингулярным радикалом или -радикал .
- в) В случае у одного есть .
Квадрика называется невырожденной, если .
Примеры в (см. выше):
(E1): Для (коническая) билинейная форма
В случае полярные пространства никогда не бывают . Следовательно .
В случае билинейная форма сводится к и . Следовательно В этом случае f -радикал является общей точкой всех касательных, так называемым узлом .
В обоих случаях и квадрика (коника) невырождена .
(E2): Для (пара линий) билинейная форма и точка пересечения.
В этом примере квадрика вырождена .
Симметрии
[ редактировать ]Квадрика — достаточно однородный объект:
- Для любой точки существует инволюционная центральная коллинеация с центром и .
Доказательство: Из-за полярное пространство является гиперплоскостью.
Линейное отображение
вызывает инволюторную центральную коллинеацию с осью и центр который оставляет инвариант.
В случае , отображение создает знакомую форму с и для любого .
Примечание:
- а) Внешняя линия, касательная или секущая отображается инволюцией по внешней, касательной и секущей линиям соответственно.
- б) точечно фиксируется .
q -подпространства и индекс квадрики
[ редактировать ]Подпространство из называется -подпространство, если
Например: точки на сфере или линии на гиперболоиде (см. ниже).
- Любые два максимальных -подпространства имеют одинаковую размерность . [5]
Пусть будет размерность максимального -подпространства затем
- Целое число называется индексом .
Теорема: (БЮКЕНХАУТ) [6]
- Для индекса невырожденной квадрики в верно следующее:
- .
Пусть будет невырожденная квадрика в , и его индекс.
- В случае квадрика называется сферой (или овалом конической, если ).
- В случае квадрика называется гиперболоидом (однолистным).
Примеры:
- а) Квадрика в с формой невырожден с индексом 1.
- б) Если полиномиальный является неприводимым над квадратичная форма порождает невырожденную квадрику в индекса 1 (сфера). Например: является неприводимым над (но не более !).
- в) В квадратичная форма порождает гиперболоид .
Обобщение квадрик: квадратичные множества
[ редактировать ]Формально определение квадрик распространять на пространства над настоящими телами (теловыми кольцами) неразумно. Потому что можно было бы получить секущие, несущие более двух точек квадрики, которая совершенно отличается от обычных квадрик. [7] [8] [9] Причиной является следующее утверждение.
- Разделительное кольцо коммутативно тогда и только тогда , когда любое уравнение , имеет не более двух решений.
Существуют обобщения квадрик: квадратичные множества . [10] Квадратичное множество — это множество точек проективного пространства с теми же геометрическими свойствами, что и квадрика: каждая прямая пересекает квадратичное множество не более чем в двух точках или содержится в этом множестве.
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Сильвио Леви Квадрики в «Геометрических формулах и фактах», выдержки из 30-го издания стандартных математических таблиц и формул CRC , CRC Press , из Центра геометрии Университета Миннесоты.
- ^ Стюарт Венит и Уэйн Бишоп, Элементарная линейная алгебра (четвертое издание) , International Thompson Publishing, 1996.
- ^ С. Лазебник и Дж. Понсе, «Локальная проективная форма гладких поверхностей и их очертания» (PDF) . , Предложение 1
- ^ Багспехер/Розенбаум стр.158
- ^ Багпачер/Розенбаум, стр.139
- ^ Ф. Букенхаут: Квадратичные множества проективного пространства , Матем. Тейчр. 110 (1969), с. 306-318.
- ^ Р. Арци : Конический в плоскостях Муфанг , Equat.Mathem. 6 (1971), с. 31-35
- ^ Э. Берц: Конические сечения в плоскостях Дезарга , Zeitschr. 78 (1962), с. 55-8
- ^ внешняя ссылка Э. Хартманн: Геометрия плоского круга , с. 123
- ^ Багспехер/Розенбаум: с. 135
Библиография
[ редактировать ]- М. Аден: Геометрия , Springer, Берлин, 2002, ISBN 978-3-540-43498-6 , с. 200.
- М. Бергер: Сборники задач по математике , ISSN 0941-3502, Springer New York, стр. 79–84.
- А. Багспачер, У. Розенбаум: Проективная геометрия , Vieweg + Teubner, Брауншвейг и др., 1992, ISBN 3-528-07241-5 , с. 159.
- П. Дембовский: Конечные геометрии , Springer, 1968, ISBN 978-3-540-61786-0 , с. 43.
- Исковских, В.А. (2001) [1994], «Квадрик» , Энциклопедия Математики , EMS Press
- Вайсштейн, Эрик В. «Квадрик» . Математический мир .

















































































































































































































































