Клин (геометрия)

Клин
Клин
Лица	2 треугольника , ; 3 четырехугольника
Края	9
Вершины	6

В твердотельной геометрии клин — это многогранник, определяемый двумя треугольниками и тремя гранями трапеции . У клина пять граней, девять ребер и шесть вершин.

Характеристики

Клин представляет собой многогранник с прямоугольным основанием, гранями которого являются два равнобедренных треугольника и две трапеции , сходящиеся в вершине ребра. ^{[ 1 ]}. Призматоид , определяется как многогранник, вершины которого лежат в двух параллельных плоскостях, а боковые грани представляют собой треугольники трапеции и параллелограммы ; ^{[ 2 ]} клин является примером призматоида, поскольку его верхний край параллелен прямоугольному основанию. ^{[ 3 ]} Объем клина $V=bh\left({\frac {a}{3}}+{\frac {c}{6}}\right),$ где находится базовый прямоугольник $a$ к $b$ , $c$ параллельна вершины длина ребра $a$ , и $h$ — высота от базового прямоугольника до края вершины. ^{[ 1 ]}

Примеры

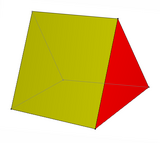
В некоторых частных случаях клин является правильной призмой , если все ребра, соединяющие треугольники, равны по длине, а треугольные грани перпендикулярны прямоугольному основанию. ^{[ 3 ]}

Клинья могут быть созданы из разложения других многогранников. Например, додекаэдр можно разделить на центральный куб с шестью клиньями, закрывающими грани куба. Ориентация клиньев такова, что грани треугольника и трапеции могут соединяться и образовывать правильный пятиугольник .

Два тупых клина можно образовать, разделив правильный тетраэдр пополам на плоскости, параллельной двум противоположным ребрам.

Особые случаи
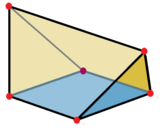Тупой клин как разделенный пополам правильный тетраэдр.	Клин, составленный из 8 треугольных граней и 2 квадратов. Его можно рассматривать как тетраэдр, дополненный двумя квадратными пирамидами .	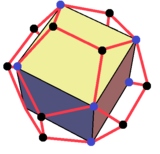Правильный додекаэдр можно разложить на центральный куб и 6 клиньев по 6 квадратным граням.

Ссылки

^ Jump up to: ^а ^б Харрис, JW; Стокер, Х. (1998). " "Клин". §4.5.2" . Справочник по математике и информатике . Нью-Йорк: Спрингер. п. 102. ИСБН 978-0-387-94746-4 .
^ Альсина, Клауди; Нельсен, Роджер Б. (2015), Математическая космическая одиссея: твердотельная геометрия в 21 веке , Математическая ассоциация Америки , стр. 85, ISBN 978-0-88385-358-0 .
^ Jump up to: ^а ^б Хоул, Вм. стр. (1893). Измерение . Джин и Ко. стр. 45.

Внешние ссылки

Вайсштейн, Эрик В. «Клин» . Математический мир .

[harris-stocker-1] Jump up to: ^а ^б Харрис, JW; Стокер, Х. (1998). " "Клин". §4.5.2" . Справочник по математике и информатике . Нью-Йорк: Спрингер. п. 102. ИСБН 978-0-387-94746-4 .

[alsina-nelsen-2] Альсина, Клауди; Нельсен, Роджер Б. (2015), Математическая космическая одиссея: твердотельная геометрия в 21 веке , Математическая ассоциация Америки , стр. 85, ISBN 978-0-88385-358-0 .

[haul-3] Jump up to: ^а ^б Хоул, Вм. стр. (1893). Измерение . Джин и Ко. стр. 45.

[ 1 ]

[ 2 ]

[ 3 ]