Закон косинусов

В тригонометрии закон косинусов (также известный как формула косинусов или правило косинусов ) связывает длины сторон треугольника с косинусом одного из его углов . Для треугольника со сторонами $a,$ $b,$ и $c,$ противоположные соответствующие углы $\alpha ,$ $\beta ,$ и $\gamma$ (см. рис. 1), закон косинусов гласит:

{\begin{aligned}c^{2}&=a^{2}+b^{2}-2ab\cos \gamma ,\\[3mu]a^{2}&=b^{2}+c^{2}-2bc\cos \alpha ,\\[3mu]b^{2}&=a^{2}+c^{2}-2ac\cos \beta .\end{aligned}}

Закон косинусов обобщает теорему Пифагора , справедливую только для прямоугольных треугольников : если $\gamma$ это прямой угол тогда $\cos \gamma =0,$ и закон косинусов сводится к $c^{2}=a^{2}+b^{2}.$

Закон косинусов полезен для решения треугольника , когда заданы все три или две стороны и прилежащий к ним угол.

Использование при решении треугольников.

Рис. 3 – Применение закона косинусов: неизвестная сторона и неизвестный угол.

Теорема используется при решении треугольников , т.е. для нахождения (см. рисунок 3):

третья сторона треугольника, если известны две стороны и угол между ними: $c={\sqrt {a^{2}+b^{2}-2ab\cos \gamma }}\,;$
углы треугольника, если известны три стороны: $\gamma =\arccos \left({\frac {a^{2}+b^{2}-c^{2}}{2ab}}\right)\,;$
третья сторона треугольника, если известны две стороны и угол, противолежащий одной из них (эту сторону можно найти также двумя применениями закона синусов ): ^[а] $a=b\cos \gamma \pm {\sqrt {c^{2}-b^{2}\sin ^{2}\gamma }}\,.$

Эти формулы дают большие ошибки округления при вычислениях с плавающей запятой , если треугольник очень острый, т. е. если $c$ мало по отношению к $a$ , а $b$ или $γ$ мало по сравнению с 1. Можно даже получить результат, немного превышающий единицу. для косинуса угла.

является результатом решения a квадратного уравнения $Третья показанная формула 2 - 2 ab cos γ + b 2 - с 2 = 0$ . Это уравнение может иметь 2, 1 или 0 положительных решений, что соответствует количеству возможных треугольников с учетом данных. Оно будет иметь два положительных решения, если $b sin γ < c < b$ , только одно положительное решение, если $c = b sin γ$ , и не иметь решения, если $c < b sin γ$ . Эти разные случаи также объясняются неоднозначностью сравнения сторон и углов .

История

Евклида Книга II «Начал» , составленная ок. 300 г. до н.э., основанный на материале, написанном на столетие или два старше, содержит геометрическую теорему, соответствующую закону косинусов, но выраженную на современном языке площадей прямоугольников; Эллинистическая тригонометрия возникла позже, а синус и косинус сами по себе впервые появились столетия спустя в Индии.

Случаи тупоугольных и остроугольных треугольников (соответствующие двум случаям отрицательного или положительного косинуса) рассматриваются отдельно в предложениях II.12 и II.13: ^[1]

Предложение 12.
В тупоугольных треугольниках квадрат на стороне, стягивающей тупой угол, больше квадратов на сторонах, содержащих тупой угол, в два раза больше прямоугольника, заключенного в одной из сторон вокруг тупого угла, а именно той, на которую падает перпендикуляр, и прямая линия, отсекаемая снаружи перпендикуляром к тупому углу.
- Евклида Элементы , перевод Томаса Л. Хита . ^[1]

Предложение 13 содержит аналогичное утверждение для остроугольных треугольников. В своем комментарии (ныне утерянном и сохранившемся лишь в виде фрагментарных цитат) Герон Александрийский представил доказательства обратного как в II.12, так и в II.13. ^[2]

Используя обозначения, показанные на рис. 2, формулировку предложения II.12 Евклида можно представить более кратко (хотя и анахронично) формулой

AB^{2}=CA^{2}+CB^{2}+2(CA)(CH).

Чтобы преобразовать это в знакомое выражение закона косинусов, замените $AB=c,$ $CA=b,$ $CB=a,$ и $CH=a\cos(\pi -\gamma )\$ $=-a\cos \gamma .$

Предложение II.13 не использовалось во времена Евклида для решения треугольников, но позже оно использовалось таким образом при решении астрономических задач аль-Бируни (11 век) и Иоганнесом де Мюрисом (14 век). ^[3] Нечто, эквивалентное сферическому закону косинусов, использовалось (но не формулировалось в целом) аль-Хорезми (9 век), аль-Баттани (9 век) и Нилакантой (15 век). ^[4]

Джамшид аль-Каши , персидский математик и астроном XV века, вычисливший самые точные тригонометрические таблицы своей эпохи, писал о решении треугольников в своем «Мифтах аль-Хисаб» ( «Ключ арифметики» , 1427 г.), включая следующий метод нахождения третья сторона с учетом двух сторон и прилежащего к ним угла: ^[5]

Другой случай , когда известны две стороны и угол между ними, а остальные неизвестны. Мы умножаем одну из сторон на синус [известного] угла один раз и на синус его дополнения, другой раз преобразуем, и вычитаем второй результат из другой стороны, если угол острый, и прибавляем его, если угол равен тупой. Затем мы возводим результат в квадрат и добавляем к нему квадрат первого результата. Извлекаем квадратный корень из суммы, чтобы получить оставшуюся часть....
- Мифтах аль- Хисаб Аль- Каши ,
перевод Нуха Айдина, Лахдара Хаммуди и Гады Бакбука ^[6]

Используя современные алгебраические обозначения и соглашения, это можно было бы записать

c={\sqrt {(b-a\cos \gamma )^{2}+(a\sin \gamma )^{2}}}

когда $\gamma$ носит острый или

c={\sqrt {\left(b+a\left|\cos \gamma \right|\right)^{2}+\left(a\sin \gamma \right)^{2}}}

когда $\gamma$ тупо. (Когда $\gamma$ это глупо, современное соглашение таково, что $\cos \gamma$ является отрицательным и $\cos(\pi -\gamma )=-\cos \gamma$ является положительным; исторически синусы и косинусы считались отрезками прямой с неотрицательной длиной.) Путем возведения в квадрат обеих сторон, расширения квадрата бинома, а затем применения тригонометрического тождества Пифагора $\cos ^{2}\gamma +\sin ^{2}\gamma =1,$ получаем знакомый закон косинусов:

{\begin{aligned}c^{2}&=b^{2}-2ba\cos \gamma +a^{2}\cos ^{2}\gamma +a^{2}\sin ^{2}\gamma \\[5mu]&=a^{2}+b^{2}-2ab\cos \gamma .\end{aligned}}

Во Франции закон косинусов иногда называют теоремой д'Аль-Каши . ^[7]^[8]

Метод Аль-Каши по сути такой же, как метод, рекомендованный для решения таких треугольников в «Китаб аль-Шакл аль-катта » Насира ад-Дина ат-Туси ( «Книга о полном четырехугольнике» , ок. 1250 г.), но с описанными шагами. явно, вместо того, чтобы оставлять детали читателю. ^[9]

Теорема была впервые записана с использованием алгебраических обозначений Франсуа Вьета в 16 веке. В начале XIX века современные алгебраические обозначения позволили записать закон косинусов в его нынешней символической форме. ^[10]

Доказательства

Используя теорему Пифагора

Случай тупого угла

Евклид доказал эту теорему, применив теорему Пифагора к каждому из двух прямоугольных треугольников на рис. 2 ( $AHB$ и $CHB$ ). Используя $d$ для обозначения отрезка $CH$ и $h$ для высоты $BH$ , треугольник $AHB$ дает нам

c^{2}=(b+d)^{2}+h^{2},

и треугольник $CHB$ дает

d^{2}+h^{2}=a^{2}.

Разложение первого уравнения дает

c^{2}=b^{2}+2bd+d^{2}+h^{2}.

Подставив в это второе уравнение, можно получить следующее:

c^{2}=a^{2}+b^{2}+2bd.

Это 12-е предложение Евклида из второй книги «Начал » . ^[11] Чтобы преобразовать его в современную форму закона косинусов, заметим, что

d=a\cos(\pi -\gamma )=-a\cos \gamma .

Случай острого угла

Доказательство Евклидом его предложения 13 идет по той же схеме, что и его доказательство предложения 12: он применяет теорему Пифагора к обоим прямоугольным треугольникам, образованным путем опускания перпендикуляра на одну из сторон, охватывающих угол $γ$ , и использует квадрат разности для упрощения .

Еще одно доказательство в остром случае

Используя больше тригонометрии, закон косинусов можно вывести, применив теорему Пифагора только один раз. Фактически, используя прямоугольный треугольник в левой части рисунка 6, можно показать, что:

{\begin{aligned}c^{2}&=(b-a\cos \gamma )^{2}+(a\sin \gamma )^{2}\\&=b^{2}-2ab\cos \gamma +a^{2}\cos ^{2}\gamma +a^{2}\sin ^{2}\gamma \\&=b^{2}+a^{2}-2ab\cos \gamma ,\end{aligned}}

используя тригонометрическое тождество $\cos ^{2}\gamma +\sin ^{2}\gamma =1.$

Это доказательство нуждается в небольшой модификации, если $b < a cos(γ)$ . В этом случае прямоугольный треугольник, к которому применяется теорема Пифагора, выходит за пределы треугольника $ABC$ . Единственное влияние, которое это оказывает на расчет, заключается в том, что величина $b - a cos(γ)$ заменяется на $a cos(γ) - b .$ Поскольку эта величина входит в расчет только через свой квадрат, остальная часть доказательства не затрагивается. Однако эта проблема возникает только тогда, когда $β$ тупой, и ее можно избежать, отразив треугольник вокруг биссектрисы $γ$ .

Ссылаясь на рис. 6, стоит отметить, что если угол, противоположный стороне $a,$ равен $α$ , то:

\tan \alpha ={\frac {a\sin \gamma }{b-a\cos \gamma }}.

Это полезно для прямого расчета второго угла, когда заданы две стороны и прилежащий угол.

С трёх высот

Рис. 5 – Остроугольный треугольник с перпендикуляром

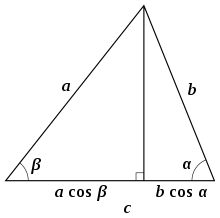
Высота , проходящая через вершину $C,$ представляет собой отрезок, перпендикулярный стороне $c$ . Расстояние от подножия высоты до вершины $А$ плюс расстояние от подножия высоты до вершины $В$ равно длине стороны $с$ (см. рис. 5). Каждое из этих расстояний можно записать как одну из других сторон, умноженную на косинус прилежащего угла: ^[12]

c=a\cos \beta +b\cos \alpha .

(Это по-прежнему верно, если $α$ или $β$ тупые, и в этом случае перпендикуляр выходит за пределы треугольника.) Умножение обеих сторон на $c$ дает

c^{2}=ac\cos \beta +bc\cos \alpha .

Те же самые шаги работают так же хорошо, если рассматривать любую из других сторон как основание треугольника:

{\begin{aligned}a^{2}&=ac\cos \beta +ab\cos \gamma ,\\[3mu]b^{2}&=bc\cos \alpha +ab\cos \gamma .\end{aligned}}

Взяв уравнение для $c^{2}$ и вычитая уравнения для $b^{2}$ и $a^{2},$

{\begin{aligned}c^{2}-a^{2}-b^{2}&={\color {BlueGreen}{\cancel {\color {Black}ac\cos \beta }}}+{\color {Peach}{\cancel {\color {Black}bc\cos \alpha }}}-{\color {BlueGreen}{\cancel {\color {Black}ac\cos \beta }}}-{\color {Peach}{\cancel {\color {Black}bc\cos \alpha }}}-2ab\cos \gamma \\c^{2}&=a^{2}+b^{2}-2ab\cos \gamma .\end{aligned}}

Это доказательство не зависит от теоремы Пифагора , поскольку оно основано только на определении косинуса в прямоугольном треугольнике и алгебраически получает квадраты длин сторон. теорему Пифагора и являются более геометрическими, рассматривая $cos Другие доказательства обычно явно ссылаются на γ$ как метку длины определенного отрезка прямой. ^[12]

рассматриваются случаи тупых и острых углов $γ$ В отличие от многих доказательств, в этом унифицировано .

Декартовы координаты

Рис. 4 – Доказательство координатной геометрии

Рассмотрим треугольник со сторонами длиной $a$ , $b$ , $c$ , где $θ$ — это угол, противоположный стороне длины $c$ . Этот треугольник можно поместить в декартову систему координат со стороной $a,$ выровненной по оси x , и углом $θ,$ расположенным в начале координат, путем нанесения на график компонентов трех точек треугольника, как показано на рис. 4:

A=(b\cos \theta ,b\sin \theta ),B=(a,0),{\text{ and }}C=(0,0).

По формуле расстояния , ^[13]

c={\sqrt {(a-b\cos \theta )^{2}+(0-b\sin \theta )^{2}}}.

Возведение в квадрат обеих сторон и упрощение

{\begin{aligned}c^{2}&=(a-b\cos \theta )^{2}+(-b\sin \theta )^{2}\\&=a^{2}-2ab\cos \theta +b^{2}\cos ^{2}\theta +b^{2}\sin ^{2}\theta \\&=a^{2}+b^{2}(\sin ^{2}\theta +\cos ^{2}\theta )-2ab\cos \theta \\&=a^{2}+b^{2}-2ab\cos \theta .\end{aligned}}

Преимущество этого доказательства в том, что оно не требует рассмотрения отдельных случаев в зависимости от того, является ли угол $γ$ острым, прямым или тупым. Однако случаи, рассмотренные отдельно в Элементах II.12–13 и позже ат-Туси, аль-Каши и другими, сами по себе могут быть объединены с использованием понятий знаковых длин и площадей и понятия знакового косинуса, без необходимости полного декартова система координат.

Используя теорему Птолемея

На схеме треугольник ABC со сторонами $AB$ = $c$ , $BC$ = $a$ и $AC$ = $b$ нарисован внутри описанной окружности, как показано на рисунке. Треугольник $ABD$ построен равным треугольнику $ABC,$ причем $AD$ = $BC$ и $BD$ = $AC$ . Перпендикуляры из $D$ и $C$ пересекают основание $AB$ в точках $E$ и $F$ соответственно. Затем:

{\begin{aligned}&BF=AE=BC\cos {\hat {B}}=a\cos {\hat {B}}\\\Rightarrow \ &DC=EF=AB-2BF=c-2a\cos {\hat {B}}.\end{aligned}}

Теперь закон косинусов выражается прямым применением теоремы Птолемея к вписанному четырехугольнику $ABCD$ :

{\begin{aligned}&AD\times BC+AB\times DC=AC\times BD\\\Rightarrow \ &a^{2}+c(c-2a\cos {\hat {B}})=b^{2}\\\Rightarrow \ &a^{2}+c^{2}-2ac\cos {\hat {B}}=b^{2}.\end{aligned}}

Очевидно, что если угол $B$ прямой , то $ABCD$ — прямоугольник, и применение теоремы Птолемея приводит к теореме Пифагора :

a^{2}+c^{2}=b^{2}.\quad

Сравнивая области

Закон косинусов можно также доказать, вычислив площади . Изменение знака по мере того, как угол $γ$ становится тупым, делает необходимым различие падежей.

Напомним, что

$а 2$ , $б 2$ , и $с 2$ – площади квадратов со сторонами $a$ , $b$ и $c$ соответственно;
если $γ$ острый, то $ab cos γ$ — площадь параллелограмма со сторонами $a$ и $b,$ образующими угол $γ′ = .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}π / 2 ⁠ - γ$ ;
если $γ$ тупой и поэтому $cos γ$ отрицательен, то $- ab cos γ$ — это площадь параллелограмма, стороны a и b которого образуют угол $γ' = γ - ⁠ π / 2 ⁠$ .

Острый случай. На рис. 7а показан семиугольник, разрезанный на более мелкие части (двумя разными способами), что дает доказательство закона косинусов. Различные части

розовым выделены области $a 2$ , $б 2$ слева и области $2 ab cos γ$ и $c 2$ справа;
синим цветом треугольник $ABC$ слева и справа;
серым цветом — вспомогательные треугольники, все конгруэнтные ABC $, одинаковое число (а именно 2) как слева ,$ так и справа.

Равенство площадей слева и справа дает

\,a^{2}+b^{2}=c^{2}+2ab\cos \gamma \,.

Тупой случай. Рисунок 7б разрезает шестиугольник на более мелкие части двумя разными способами, что дает доказательство закона косинусов в случае, когда угол $γ$ тупой. У нас есть

розовым выделены области $a 2$ , $б 2$ , и $-2 ab cos γ$ слева и $c 2$ справа;
синим цветом треугольник $ABC$ дважды, слева и справа.

Равенство площадей слева и справа дает

\,a^{2}+b^{2}-2ab\cos(\gamma )=c^{2}.

Строгое доказательство должно будет включать доказательства того, что различные фигуры конгруэнтны и, следовательно, имеют одинаковую площадь. Для этого воспользуемся теорией равных треугольников .

Использование геометрии круга

Рис. 8а – Треугольник $ABC$ (розовый), вспомогательный круг (голубой) и вспомогательный прямоугольный треугольник (желтый)

Рис. 8б – Треугольник $ABC$ (розовый), вспомогательный круг (голубой) и два вспомогательных прямоугольных треугольника (желтый)

Используя геометрию круга , можно дать более геометрическое доказательство, чем используя одну лишь теорему Пифагора . Алгебраические манипуляции (в частности, биномиальная теорема ) избегаются.

Случай острого угла $γ$ , где $a > 2 b cos γ$ . Опустите перпендикуляр из $A$ на $a$ = $BC$ , создав отрезок длиной $b cos γ$ . Дублируйте прямоугольный треугольник , чтобы сформировать равнобедренный треугольник $ACP$ . Постройте круг с центром $A$ и радиусом $b$ и его касательной $h = BH$ проходящей через $B.$ , Касательная $h$ образует прямой угол с радиусом $b$ Евклида ( Начала : Книга 3, Предложение 18; или см. здесь ), поэтому желтый треугольник на рисунке 8 является прямым. Примените теорему Пифагора, чтобы получить

c^{2}=b^{2}+h^{2}.

Затем используйте теорему о касательном секущем Евклида ( Начала : Книга 3, Предложение 36), которая гласит, что квадрат касательной, проходящей через точку $B$ вне круга, равен произведению двух отрезков прямой (из $B$ ), созданных любым секущим . круга $B.$ через В данном случае: $БХ 2 = BC \cdot BP$ , или

h^{2}=a(a-2b\cos \gamma ).

Подстановка в предыдущее уравнение дает закон косинусов:

c^{2}=b^{2}+a(a-2b\cos \gamma ).

Обратите внимание, что $ч 2$ — степень точки $B$ относительно окружности. Использование теоремы Пифагора и теоремы о касательном секущем можно заменить однократным применением теоремы о мощности точки .

Случай острого угла $γ$ , где $a < 2 b cos γ$ . Опустите перпендикуляр из $A$ на $a$ = $BC$ , создав отрезок длиной $b cos γ$ . Дублируйте прямоугольный треугольник , чтобы сформировать равнобедренный треугольник $ACP$ . Постройте круг с центром $A$ и радиусом $b$ и хордой , проходящей через $B,$ перпендикулярной $c = AB,$ половина которой равна $h = BH .$ Примените теорему Пифагора, чтобы получить

b^{2}=c^{2}+h^{2}.

Теперь используйте теорему о хорде Евклида ( Начала : Книга 3, Предложение 35), которая гласит, что если две хорды пересекаются, произведение двух отрезков, полученных на одной хорде, равно произведению двух отрезков, полученных на другой хорде. . В данном случае: $БХ 2 = BC \cdot BP,$ или

h^{2}=a(2b\cos \gamma -a).

Подстановка в предыдущее уравнение дает закон косинусов:

b^{2}=c^{2}+a(2b\cos \gamma -a)\,.

Обратите внимание, что степень точки $B$ относительно окружности имеет отрицательное значение $— h 2$ .

Случай тупого угла $γ$ . В этом доказательстве напрямую используется сила точечной теоремы, без вспомогательных треугольников, полученных путем построения касательной или хорды. Постройте круг с центром $B$ и радиусом $a$ см. рисунок 9), который пересекает секущие через $A$ и $C$ в $C$ и $K.$ ( Степень точки А $AB$ относительно окружности равна $как 2 - до нашей эры 2$ и $АС \cdot АК$ . Поэтому,

{\begin{aligned}c^{2}-a^{2}&{}=b(b+2a\cos(\pi -\gamma ))\\&{}=b(b-2a\cos \gamma ),\end{aligned}}

что является законом косинусов.

Используя алгебраические меры для отрезков прямых (допуская отрицательные числа в качестве длин отрезков), случай тупого угла ( $CK > 0$ ) и острого угла ( $CK < 0$ ) можно рассматривать одновременно.

Используя закон синусов

Закон косинусов можно доказать алгебраически на основе закона синусов и нескольких стандартных тригонометрических тождеств. ^[14] Для начала сложим три угла треугольника в прямой угол ( $\alpha +\beta +\gamma =\pi$ радианы). Таким образом, согласно тождествам суммы углов для синуса и косинуса,

{\begin{alignedat}{3}\sin \gamma &={\phantom {-}}\sin(\pi -\gamma )&&={\phantom {-}}\sin(\alpha +\beta )&&=\sin \alpha \,\cos \beta +\cos \alpha \,\sin \beta ,\\[5mu]\cos \gamma &=-\cos(\pi -\gamma )&&=-\cos(\alpha +\beta )&&=\sin \alpha \,\sin \beta -\cos \alpha \,\cos \beta .\end{alignedat}}

Возводя в квадрат первое из этих тождеств, затем подставляя $\cos \alpha \,\cos \beta ={}$ $\sin \alpha \,\sin \beta -\cos \gamma$ со второго и, наконец, заменив $\cos ^{2}\alpha +\sin ^{2}\alpha ={}$ $\cos ^{2}\beta +\sin ^{2}\beta =1,$ тригонометрическое тождество Пифагора имеем:

{\begin{aligned}\sin ^{2}\gamma &=(\sin \alpha \,\cos \beta +\cos \alpha \,\sin \beta )^{2}\\[3mu]&=\sin ^{2}\alpha \,\cos ^{2}\beta +2\sin \alpha \,\sin \beta \,\cos \alpha \,\cos \beta +\cos ^{2}\alpha \,\sin ^{2}\beta \\[3mu]&=\sin ^{2}\alpha \,\cos ^{2}\beta +2\sin \alpha \,\sin \beta (\sin \alpha \,\sin \beta -\cos \gamma )+\cos ^{2}\alpha \,\sin ^{2}\beta \\[3mu]&=\sin ^{2}\alpha (\cos ^{2}\beta +\sin ^{2}\beta )+\sin ^{2}\beta (\cos ^{2}\alpha +\sin ^{2}\alpha )-2\sin \alpha \,\sin \beta \,\cos \gamma \\[3mu]&=\sin ^{2}\alpha +\sin ^{2}\beta -2\sin \alpha \,\sin \beta \,\cos \gamma .\end{aligned}}

Закон синусов утверждает, что

{\frac {a}{\sin \alpha {\vphantom {\beta }}}}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma {\vphantom {\beta }}}}=k,

поэтому, чтобы доказать закон косинусов, мы умножаем обе части нашего предыдущего тождества на $k^{2}\colon$

{\begin{aligned}\sin ^{2}\gamma {\frac {c^{2}}{\sin ^{2}\gamma }}&=\sin ^{2}\alpha {\frac {a^{2}}{\sin ^{2}\alpha }}+\sin ^{2}\beta {\frac {b^{2}}{\sin ^{2}\beta }}-2\sin \alpha \,\sin \beta \,\cos \gamma {\frac {ab}{\sin \alpha \,\sin \beta {\vphantom {\sin ^{2}}}}}\\[10mu]c^{2}&=a^{2}+b^{2}-2ab\cos \gamma .\end{aligned}}

На этом доказательство завершается.

Использование векторов

Обозначим

{\overrightarrow {CB}}={\vec {a}},\ {\overrightarrow {CA}}={\vec {b}},\ {\overrightarrow {AB}}={\vec {c}}

Поэтому,

{\vec {c}}={\vec {a}}-{\vec {b}}

Взяв скалярное произведение каждой стороны с собой:

{\vec {c}}\cdot {\vec {c}}=({\vec {a}}-{\vec {b}})\cdot ({\vec {a}}-{\vec {b}})

\Vert {\vec {c}}\Vert ^{2}=\Vert {\vec {a}}\Vert ^{2}+\Vert {\vec {b}}\Vert ^{2}-2\,{\vec {a}}\cdot {\vec {b}}

Использование личности

{\vec {u}}\cdot {\vec {v}}=\Vert {\vec {u}}\Vert \,\Vert {\vec {v}}\Vert \cos \angle ({\vec {u}},\ {\vec {v}})

приводит к

\Vert {\vec {c}}\Vert ^{2}=\Vert {\vec {a}}\Vert ^{2}+{\Vert {\vec {b}}\Vert }^{2}-2\,\Vert {\vec {a}}\Vert \!\;\Vert {\vec {b}}\Vert \cos \angle ({\vec {a}},\ {\vec {b}})

Результат следующий.

Равнобедренный случай

Когда $a = b$ , т. е. когда треугольник равнобедренный, причем две стороны, лежащие на угле $γ,$ равны, закон косинусов существенно упрощается. А именно, потому $что 2 + б 2 = 2 а 2 = 2 ab$ , закон косинусов принимает вид

\cos \gamma =1-{\frac {c^{2}}{2a^{2}}}

или

c^{2}=2a^{2}(1-\cos \gamma ).

Аналог тетраэдров

Дан произвольный тетраэдр , четыре грани которого имеют площади $A$ , $B$ , $C$ и $D$ с двугранным углом . $\varphi _{ab}$ между гранями $A$ и $B$ и т. д. многомерный аналог закона косинусов: ^[15]

A^{2}=B^{2}+C^{2}+D^{2}-2\left(BC\cos \varphi _{bc}+CD\cos \varphi _{cd}+DB\cos \varphi _{db}\right).

Версия подходит для небольших углов

Когда угол $γ$ мал, а смежные стороны $a$ и $b$ имеют одинаковую длину, правая часть стандартной формы закона косинусов подвергается катастрофическому сокращению в числовых приближениях. В ситуациях, когда это важно, может оказаться полезной математически эквивалентная версия закона косинусов, подобная формуле хаверсинуса :

{\begin{aligned}c^{2}&=(a-b)^{2}+4ab\sin ^{2}\left({\frac {\gamma }{2}}\right)\\&=(a-b)^{2}+4ab\operatorname {haversin} (\gamma ).\end{aligned}}

В пределе бесконечно малого угла закон косинусов вырождается в длины дуги окружности формулу $c = a γ$ .

В сферической и гиперболической геометрии

Сферический треугольник решается по закону косинусов.

Версии, аналогичные закону косинусов для евклидовой плоскости, справедливы и на единичной сфере и в гиперболической плоскости. В сферической геометрии треугольник определяется тремя точками $u$ , $v$ и $w$ на единичной сфере и дугами больших кругов, соединяющими эти точки. Если эти большие круги образуют углы $A$ , $B$ и $C$ с противоположными сторонами $a$ , $b$ , $c,$ то сферический закон косинусов утверждает, что выполняются оба следующих соотношения:

{\begin{aligned}\cos a&=\cos b\cos c+\sin b\sin c\cos A\\\cos A&=-\cos B\cos C+\sin B\sin C\cos a.\end{aligned}}

В гиперболической геометрии пара уравнений известна под общим названием гиперболический закон косинусов . Первое - это

\cosh a=\cosh b\cosh c-\sinh b\sinh c\cos A

где $sinh$ и $cosh$ — гиперболические синус и косинус , а второй —

\cos A=-\cos B\cos C+\sin B\sin C\cosh a.

Как и в евклидовой геометрии, можно использовать закон косинусов для определения углов $A$ , $B$ , $C$ по знанию сторон $a$ , $b$ , $c$ . В отличие от евклидовой геометрии, в обеих неевклидовых моделях возможен и обратный процесс: углы $A$ , $B$ , $C$ определяют стороны $a$ , $b$ , $c$ .

Многогранники

Закон косинусов можно обобщить на все многогранники , рассмотрев любой многогранник с векторными сторонами и применив теорему о дивергенции. . ^[16]

См. также

Примечания

^ Указанные стороны $b,c$ и угол $\gamma ,$ $\sin \beta$ можно найти с помощью закона синусов, оставляя до двух вариантов угла $\beta$ . Любой выбор определяет $\alpha$ потому что сумма трех внутренних углов образует прямой угол. Окончательно $a$ можно найти из $c,\gamma ,\alpha$ другим применением закона синусов.

Ссылки

^ Jump up to: ^а ^б Евклид. Томас Л. Хит (ред.). «Элементы» . Перевод Томаса Л. Хита . Проверено 24 января 2023 г.
^ Хит, Томас (1956) [1908]. "Введение" . Тринадцать книг элементов Евклида (2-е изд.).
^ Кеннеди, ES; Мурувва, Ахмад (1958). «Бируни о солнечном уравнении». Журнал ближневосточных исследований . 17 (2): 112–121. JSTOR 542617 .
Йоханнес де Мюрис благодарит анонимного автора за соответствующий раздел своей работы De Arte Mesurandi . Видеть Ван Браммелен, Глен (2009). Математика неба и земли . Издательство Принстонского университета. стр. 240–241.
^ Ван Браммелен, Глен (2012). Небесная математика: Забытое искусство сферической тригонометрии . Издательство Принстонского университета. п. 98.
^ Азарян, Мохаммад К. (2000). «Мефтаб Аль-Хесаб: Краткое содержание» (PDF) . Миссурийский журнал математических наук . 12 (2): 75–95. дои : 10.35834/2000/1202075 .
^ Айдын, Нух; Хаммуди, Лахдар; Бакбук, Гада (2020). «Мифтах аль-Хисаб» Аль-Каши, Том II: Геометрия . Биркхойзер. п. 31. дои : 10.1007/978-3-030-61330-3 .
^ Пиковер, Клиффорд А. (2009). Книга по математике: от Пифагора до 57-го измерения . Стерлинг Паблишинг Компани, Инк. 106. ИСБН 9781402757969 .
^ Первая программа по общей математике (на французском языке). Министерство национального образования и молодежи. 2022.стр. 11, 12.
^ Нашир ад-Дин аль-Туси (1891 г.). «Гл. 3.2: О том, как вычислить стороны и углы треугольника друг относительно друга» . Трактат о четырехугольнике, приписываемый Насируддинелю-Тусси (на французском языке). Перевод Каратеодори, Александр-паша . Типография и литография Османие. п. 69. Даём две стороны и угол. [...] Что, если данный угол заключен между двумя данными сторонами, как угол A заключен между двумя сторонами AB AC, опустите перпендикуляр BE от B до AC. Таким образом, у вас будет прямоугольный треугольник [BEA], у которого мы знаем сторону AB и угол A; мы выведем BE, EA и, таким образом, вернемся к одному из предыдущих случаев; в. имеет. д. в случае, когда известны BE, CE; тогда мы будем знать BC и угол C, как мы объясняли [Учитывая [...], что угол A находится между двумя сторонами AB AC, опустите от B до AC перпендикуляр BE. Таким образом, у вас будет прямоугольный треугольник [BEA], у которого мы знаем сторону AB и угол A; в этом треугольнике вычисляют BE, EA, и задача сводится к одному из предыдущих случаев; то есть к случаю, когда известны BE, CE; таким образом, мы будем знать BC и угол C, как мы объяснили.]
^ Например, в Карно, Лазар (1803). Позиционная геометрия . ЖБМ Дюпра. п. 202.
^ Версия Java-апплета профессора Д. Э. Джойса из Университета Кларка.
^ Jump up to: ^а ^б Александр Богомольный приписывает это доказательство учителю Джону Молокачу (2011), но оно может быть старше. Богомольный, Александр . «Закон косинусов (независимый от теоремы Пифагора)» . Разрежьте узел . Проверено 9 января 2024 г.
^ Уайли, Кларенс Рэймонд (1955). Плоская тригонометрия . МакГроу-Хилл. §9.1 Закон косинусов, стр. 195–198. LCCN 54-11278 .
^ Бертон, LJ (1949). «Законы синусов и косинусов». Американский математический ежемесячник . 56 (8): 550–551. JSTOR 2305533 .
^ Кейси, Джон (1889). Трактат о сферической тригонометрии: и ее применении к геодезии и астрономии с многочисленными примерами . Лондон: Лонгманс, Грин и компания. п. 133.
^ Коллинз, Л; Ослер, Т (2011). «Закон косинусов, обобщенный для любого многоугольника и любого многогранника». Математический вестник . 95 (533): 240–243. JSTOR 23248682 .

Внешние ссылки

[1] Указанные стороны $b,c$ и угол $\gamma ,$ $\sin \beta$ можно найти с помощью закона синусов, оставляя до двух вариантов угла $\beta$ . Любой выбор определяет $\alpha$ потому что сумма трех внутренних углов образует прямой угол. Окончательно $a$ можно найти из $c,\gamma ,\alpha$ другим применением закона синусов.

[Euclid-Heath-Elements_Book_II_Propositions-2] Jump up to: ^а ^б Евклид. Томас Л. Хит (ред.). «Элементы» . Перевод Томаса Л. Хита . Проверено 24 января 2023 г.

[3] Хит, Томас (1956) [1908]. "Введение" . Тринадцать книг элементов Евклида (2-е изд.).

[4] Кеннеди, ES; Мурувва, Ахмад (1958). «Бируни о солнечном уравнении». Журнал ближневосточных исследований . 17 (2): 112–121. JSTOR 542617 .
Йоханнес де Мюрис благодарит анонимного автора за соответствующий раздел своей работы De Arte Mesurandi . Видеть Ван Браммелен, Глен (2009). Математика неба и земли . Издательство Принстонского университета. стр. 240–241.

[5] Ван Браммелен, Глен (2012). Небесная математика: Забытое искусство сферической тригонометрии . Издательство Принстонского университета. п. 98.

[6] Азарян, Мохаммад К. (2000). «Мефтаб Аль-Хесаб: Краткое содержание» (PDF) . Миссурийский журнал математических наук . 12 (2): 75–95. дои : 10.35834/2000/1202075 .

[7] Айдын, Нух; Хаммуди, Лахдар; Бакбук, Гада (2020). «Мифтах аль-Хисаб» Аль-Каши, Том II: Геометрия . Биркхойзер. п. 31. дои : 10.1007/978-3-030-61330-3 .

[Pickover-8] Пиковер, Клиффорд А. (2009). Книга по математике: от Пифагора до 57-го измерения . Стерлинг Паблишинг Компани, Инк. 106. ИСБН 9781402757969 .

[9] Первая программа по общей математике (на французском языке). Министерство национального образования и молодежи. 2022.стр. 11, 12.

[10] Нашир ад-Дин аль-Туси (1891 г.). «Гл. 3.2: О том, как вычислить стороны и углы треугольника друг относительно друга» . Трактат о четырехугольнике, приписываемый Насируддинелю-Тусси (на французском языке). Перевод Каратеодори, Александр-паша . Типография и литография Османие. п. 69. Даём две стороны и угол. [...] Что, если данный угол заключен между двумя данными сторонами, как угол A заключен между двумя сторонами AB AC, опустите перпендикуляр BE от B до AC. Таким образом, у вас будет прямоугольный треугольник [BEA], у которого мы знаем сторону AB и угол A; мы выведем BE, EA и, таким образом, вернемся к одному из предыдущих случаев; в. имеет. д. в случае, когда известны BE, CE; тогда мы будем знать BC и угол C, как мы объясняли [Учитывая [...], что угол A находится между двумя сторонами AB AC, опустите от B до AC перпендикуляр BE. Таким образом, у вас будет прямоугольный треугольник [BEA], у которого мы знаем сторону AB и угол A; в этом треугольнике вычисляют BE, EA, и задача сводится к одному из предыдущих случаев; то есть к случаю, когда известны BE, CE; таким образом, мы будем знать BC и угол C, как мы объяснили.]

[11] Например, в Карно, Лазар (1803). Позиционная геометрия . ЖБМ Дюпра. п. 202.

[Joyce-12] Версия Java-апплета профессора Д. Э. Джойса из Университета Кларка.

[ctk-13] Jump up to: ^а ^б Александр Богомольный приписывает это доказательство учителю Джону Молокачу (2011), но оно может быть старше. Богомольный, Александр . «Закон косинусов (независимый от теоремы Пифагора)» . Разрежьте узел . Проверено 9 января 2024 г.

[14] Уайли, Кларенс Рэймонд (1955). Плоская тригонометрия . МакГроу-Хилл. §9.1 Закон косинусов, стр. 195–198. LCCN 54-11278 .

[15] Бертон, LJ (1949). «Законы синусов и косинусов». Американский математический ежемесячник . 56 (8): 550–551. JSTOR 2305533 .

[16] Кейси, Джон (1889). Трактат о сферической тригонометрии: и ее применении к геодезии и астрономии с многочисленными примерами . Лондон: Лонгманс, Грин и компания. п. 133.

[17] Коллинз, Л; Ослер, Т (2011). «Закон косинусов, обобщенный для любого многоугольника и любого многогранника». Математический вестник . 95 (533): 240–243. JSTOR 23248682 .

[а]

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]