Теория кабеля

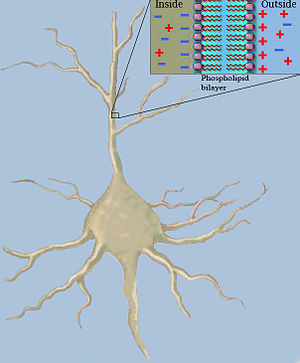
В нейробиологии классическая кабельная теория использует математические модели для расчета электрического тока (и сопутствующего напряжения ) вдоль пассивного кабеля. [а] нейриты , особенно дендриты , которые получают синаптические сигналы в разных местах и в разное время. Оценки сделаны путем моделирования дендритов и аксонов как цилиндров, состоящих из сегментов с емкостями. и сопротивления объединены параллельно (см. рис. 1). Емкость нейронного волокна возникает потому, что электростатические силы действуют через очень тонкий липидный бислой (см. рисунок 2). Сопротивление последовательно вдоль волокна Это связано со значительным сопротивлением аксоплазмы движению электрического заряда .
История
[ редактировать ]Теория кабеля в вычислительной нейробиологии уходит своими корнями в 1850-е годы, когда профессор Уильям Томсон (позже известный как лорд Кельвин) начал разрабатывать математические модели затухания сигнала в подводных (подводных) телеграфных кабелях. Модели напоминали уравнения в частных производных, которые Фурье использовал для описания теплопроводности в проводе.
В 1870-х годах Германн предпринял первые попытки смоделировать нейронов, электротонические потенциалы также сосредоточив внимание на аналогиях с теплопроводностью. Однако именно Хорвег первым обнаружил аналогии с подводными кабелями Кельвина в 1898 году, а затем Герман и Кремер независимо разработали кабельную теорию для нейронных волокон в начале 20 века. Дальнейшие математические теории проводимости нервных волокон, основанные на теории кабеля, были разработаны Коулом и Ходжкиным (1920–1930-е годы), Оффнером и др. (1940) и Раштон (1951).
Экспериментальные доказательства важности кабельной теории в моделировании поведения аксонов начали появляться в 1930-х годах в результате работ Коула, Кертиса, Ходжкина, сэра Бернарда Каца , Раштона, Тасаки и других. Двумя ключевыми статьями этой эпохи являются работы Дэвиса и Лоренте де Но (1947) и Ходжкина и Раштона (1946).
В 1950-е годы были усовершенствованы методы измерения электрической активности отдельных нейронов . Таким образом, теория кабеля стала важной для анализа данных, собранных при внутриклеточных микроэлектродных записях, и для анализа электрических свойств дендритов нейронов . Такие ученые, как Кумбс, Экклс , Фатт, Фрэнк, Фуортес и другие, теперь в значительной степени полагались на теорию кабеля, чтобы получить представление о функциональном состоянии нейронов и помочь им при планировании новых экспериментов.
еще более сложные модели нейронов Позже теория кабеля с ее математическими производными позволила исследовать таким исследователям, как Джек, Ралл , Редман, Ринзель, Идан Сегев, Таквелл, Белл и Ианнелла. Совсем недавно теория кабеля была применена для моделирования электрической активности в связанных нейронах белого вещества мозга. [1]
Вывод уравнения кабеля
[ редактировать ]Обратите внимание, что существуют различные соглашения о r m .Здесь r m и c m , как указано выше, измеряются на единицу длины мембраны (на метр (м)). Таким образом, r m измеряется в ом ·метрах (Ом·м), а см – в фарадах на метр (Ф/м). В отличие от R m (в Ω·m 2 ) и C м (в Ф/м 2 ), которые представляют собой удельное сопротивление и емкость соответственно одной единицы площади мембраны (в м 2 ). Таким образом, если известен радиус a , аксона [б] тогда его окружность равна 2 πa , а r m и cm значения можно рассчитать как:
| ( 1 ) |
| ( 2 ) |
Эти отношения имеют смысл интуитивно, поскольку чем больше окружность аксона, тем больше площадь выхода заряда через его мембрану и, следовательно, тем меньше сопротивление мембраны (деление R m на 2 πa ); и тем больше мембран доступно для хранения заряда (умножая C m на 2 πa ).Удельное электрическое сопротивление l ρ ( в аксоплазмы позволяет рассчитать продольное внутриклеточное сопротивление на единицу длины r l Ом·м −1 ) по уравнению:
| ( 3 ) |
Чем больше площадь поперечного сечения аксона, πa 2 , чем больше путей прохождения заряда через аксоплазму и тем ниже аксоплазматическое сопротивление.
В нескольких важных направлениях расширения классической кабельной теории недавно появилось введение эндогенных структур для анализа эффектов поляризации белков внутри дендритов и различного распределения синаптических входов на дендритной поверхности нейрона.
Чтобы лучше понять, как выводится уравнение кабеля, сначала еще больше упростите теоретический нейрон и представим, что он имеет идеально герметичную мембрану ( r m =∞) без потерь тока наружу и без емкости ( c m = 0). Ток, подаваемый в волокно [с] в положении x = 0 будет двигаться вдоль внутренней части волокна без изменений. Отойдя от точки подачи и используя закон Ома ( V = IR ), мы можем рассчитать изменение напряжения как:
| ( 4 ) |
где отрицательный результат, потому что ток течет вниз по градиенту потенциала.
Позволяя Δx стремиться к нулю и имея бесконечно малые приращения x , можно записать ( 4 ) как:
| ( 5 ) |
или
| ( 6 ) |
Возвращать меня . обратно в картину — все равно, что проделывать дырки в садовом шланге Чем больше отверстий, тем быстрее вода будет выходить из шланга, и тем меньше воды пройдет от начала шланга до конца. Точно так же в аксоне часть тока, проходящего через аксоплазму в продольном направлении, уходит через мембрану.
Если i m — ток, выходящий через мембрану на единицу длины, м, то общий ток, уходящий на y единиц, должен быть y·i m . Таким образом, изменение тока в аксоплазме Δ i l на расстоянии Δ x от положения x =0 можно записать как:
| ( 7 ) |
или, используя непрерывные, бесконечно малые приращения:
| ( 8 ) |
может быть выражено еще одной формулой, включая емкость. Емкость вызовет поток заряда (тока) к мембране со стороны цитоплазмы. Этот ток обычно называют током смещения (здесь он обозначается .) Поток будет иметь место только до тех пор, пока не будет достигнута емкость мембраны. тогда можно выразить как:
| ( 9 ) |
где - емкость мембраны и это изменение напряжения с течением времени. Ток, проходящий через мембрану ( ) можно выразить как:
| ( 10 ) |
и потому что следующее уравнение для можно получить, если не подать дополнительный ток от электрода:
| ( 11 ) |
где представляет собой изменение продольного тока на единицу длины.
Объединение уравнений ( 6 ) и ( 11 ) дает первую версию уравнения кабеля:
| ( 12 ) |
(УЧП) второго порядка которое представляет собой уравнение в частных производных .
Путем простой перестановки уравнения ( 12 ) (см. ниже) можно получить два важных члена, а именно константу длины (иногда называемую пространственной константой), обозначаемую и постоянная времени, обозначаемая . Следующие разделы посвящены этим терминам.
Постоянная длина
[ редактировать ]Константа длины, (лямбда) — параметр, указывающий, насколько сильно стационарный ток будет влиять на напряжение вдоль кабеля. Чем больше значение , тем дальше будет течь заряд. Константу длины можно выразить как:
| ( 13 ) |
Чем больше сопротивление мембраны r m , тем больше значение , и тем больше тока останется внутри аксоплазмы и будет проходить через аксон в продольном направлении. Чем выше аксоплазматическая резистентность, , тем меньше значение , тем труднее будет току проходить через аксоплазму и тем короче ток сможет пройти.Можно решить уравнение ( 12 ) и прийти к следующему уравнению (которое справедливо в установившихся условиях, т.е. когда время приближается к бесконечности):
| ( 14 ) |
Где это деполяризация в (точка подачи тока), e — экспоненциальная константа (приблизительное значение 2,71828) и - напряжение на заданном расстоянии x от x =0. Когда затем
| ( 15 ) |
и
| ( 16 ) |
это означает, что когда мы измеряем на расстоянии от мы получаем
| ( 17 ) |
Таким образом всегда составляет 36,8 процента от .
Постоянная времени
[ редактировать ]Нейробиологам часто интересно узнать, насколько быстро меняется мембранный потенциал. , изменения аксона в ответ на изменения тока, инжектируемого в аксоплазму. Постоянная времени, , — это индекс, предоставляющий информацию об этом значении. можно рассчитать как:
| ( 18 ) |
Чем больше емкость мембраны, , чем больший ток потребуется для зарядки и разрядки участка мембраны и тем дольше будет длиться этот процесс. Чем больше сопротивление мембраны , тем труднее току вызвать изменение мембранного потенциала. Таким образом, чем выше тем медленнее может распространяться нервный импульс. Это означает, что мембранный потенциал (напряжение на мембране) больше отстает от инжекции тока. Время отклика варьируется от 1–2 миллисекунд в нейронах, обрабатывающих информацию, требующую высокой временной точности, до 100 миллисекунд и более. Типичное время ответа составляет около 20 миллисекунд.
Общая форма и математическая структура
[ редактировать ]Если умножить уравнение ( 12 ) на по обе стороны от знака равенства получаем:
| ( 19 ) |
и признать с левой стороны и на правой стороне. Уравнение кабеля теперь можно записать в его, возможно, наиболее известной форме:
| ( 20 ) |
Это одномерное уравнение теплопроводности или уравнение диффузии , для которого было разработано множество методов решения, таких как функции Грина и методы Фурье.
Это также частный вырожденный случай уравнения Телеграфера , где индуктивность исчезает, а скорость распространения сигнала бесконечен.
См. также
[ редактировать ]- Нанофизиология
- Аксон
- Бидоменная модель
- Биоэлектрохимия
- Модель биологического нейрона
- Дендрит
- Модель Ходжкина – Хаксли
- Мембранный потенциал
- Монодоменная модель
- Уравнение Нернста – Планка
- Патч-зажим
- Сальтаторная проводимость
- Солитонная модель в нейробиологии
Ссылки
[ редактировать ]- ^ Дуглас, ПК; Дуглас, Д.Б. (2019). «Пересмотр пространственных приоритетов в оценке источника ЭЭГ: способствует ли белое вещество ритмам ЭЭГ?» . 2019 7-я Международная зимняя конференция по интерфейсу «мозг-компьютер» (BCI) . стр. 1–12. arXiv : 2111.08939 . дои : 10.1109/IWW-BCI.2019.8737307 . ISBN 978-1-5386-8116-9 . S2CID 195064621 .
- Познанский, Роман Р. (2013). Математическая нейронаука . Сан-Диего [Калифорния]: Academic Press.
- Таквелл, Генри К. (1988). Введение в теоретическую нейробиологию . Кембридж [Кембриджшир]: Издательство Кембриджского университета. ISBN 978-0521350969 .
- де Но, Рафаэль Лоренте (1947). Изучение физиологии нервов . Исследования Института медицинских исследований Рокфеллера. Перепечатки. Рокфеллеровский институт медицинских исследований. стр. Часть I, 131:1–496, Часть II, 132:1–548. ISBN 9780598674722 . OCLC 6217290 .
- Лазаревич Иван Александрович; Казанцев, Виктор Б. (2013). «Дендритный переход сигнала, индуцированный внутриклеточным зарядом в неоднородностях». Физ. Преподобный Е. 88 (6): 062718.arXiv : 1308.0821 . Бибкод : 2013PhRvE..88f2718L . дои : 10.1103/PhysRevE.88.062718 . ПМИД 24483497 . S2CID 13353454 .
- Дуглас, ПК; Дуглас, Дэвид Б. (2019). «Пересмотр пространственных приоритетов в оценке источника ЭЭГ: способствует ли белое вещество ритмам ЭЭГ?». 2019 7-я Международная зимняя конференция по интерфейсу «мозг-компьютер» (BCI) . Том. 88. стр. 1–12. arXiv : 2111.08939 . дои : 10.1109/IWW-BCI.2019.8737307 . ISBN 978-1-5386-8116-9 . S2CID 195064621 .
Примечания
[ редактировать ]- ^ Пассивный здесь означает, что сопротивление мембраны не зависит от напряжения. Однако недавние эксперименты (Стюарт и Сакманн, 1994) с дендритными мембранами показали, что многие из них оснащены потенциалзависимыми ионными каналами , что делает сопротивление мембраны зависимым от напряжения. Следовательно, возникла необходимость обновить классическую теорию кабелей, чтобы учесть тот факт, что большинство дендритных мембран не являются пассивными.
- ^ Классическая теория кабеля предполагает, что волокно имеет постоянный радиус на моделируемом расстоянии.
- ^ Классическая теория кабеля предполагает, что входные сигналы (обычно подаваемые с помощью микроустройства) представляют собой токи, которые можно суммировать линейно. Эта линейность не распространяется на изменения проводимости синаптической мембраны.









































