Нелинейная оптика

Структура кристалла KTP , вид по оси b, используемого для генерации второй гармоники.

Нелинейная оптика ( НЛО ) — раздел оптики , описывающий поведение света в нелинейных средах, то есть средах, в которых плотность поляризации P нелинейно реагирует на электрическое поле E света. Нелинейность обычно наблюдается только при очень высоких интенсивностях света (когда электрическое поле света >10 ⁸ В/м и, таким образом, сравнимо с атомным электрическим полем ~10 ¹¹ В/м), например, обеспечиваемые лазерами . Ожидается, что выше предела Швингера сам вакуум станет нелинейным. В нелинейной оптике принцип суперпозиции больше не выполняется.

История

предсказанным в 1931 году, было двухфотонное поглощение Первым нелинейно-оптическим эффектом , Марией Гепперт Майер , но он оставался неисследованной теоретической диковинкой до 1961 года и почти одновременного наблюдения двухфотонного поглощения в Bell Labs. и открытие генерации второй гармоники Питером Франкеном и др. в Мичиганском университете , вскоре после создания Теодором Мейманом первого лазера . Однако некоторые нелинейные эффекты были обнаружены еще до разработки лазера. Теоретические основы многих нелинейных процессов впервые были описаны в . монографии Бломбергена «Нелинейная оптика»

Нелинейные оптические процессы

Нелинейная оптика объясняет нелинейную реакцию таких свойств, как частота , поляризация, фаза или путь падающего света. Эти нелинейные взаимодействия приводят к множеству оптических явлений:

Процессы смешения частот

• Генерация второй гармоники (ГВГ), или удвоение частоты , генерация света с удвоенной частотой (половина длины волны), два фотона разрушаются, создавая один фотон с вдвое большей частотой.
• Генерация третьей гармоники (ГТГ), генерация света с утроенной частотой (одна треть длины волны), три фотона разрушаются, создавая один фотон с втрое большей частотой.
• Генерация высоких гармоник (HHG), генерация света с частотами, намного превышающими исходные (обычно в 100–1000 раз выше).
• Генерация суммарной частоты (SFG), генерация света с частотой, которая является суммой двух других частот (SHG является частным случаем этого).
• Генерация разностной частоты (DFG), генерация света с частотой, которая является разницей между двумя другими частотами.
• Оптическое параметрическое усиление (ОПА), усиление входного сигнала при наличии более высокочастотной волны накачки с одновременной генерацией холостой волны (можно рассматривать как DFG).
• Оптическая параметрическая генерация (ОПО), генерация сигнала и холостой волны с помощью параметрического усилителя в резонаторе (без входного сигнала).
• Оптическая параметрическая генерация (OPG), подобная параметрической генерации, но без резонатора, с использованием вместо этого очень высокого коэффициента усиления.
• Генерация полугармоники , особый случай OPO или OPG, когда сигнал и холостой ход вырождаются на одной частоте,
• Спонтанное параметрическое преобразование с понижением частоты (SPDC), усиление вакуумных колебаний в режиме низкого усиления.
• Оптическое выпрямление (ОР), генерация квазистатических электрических полей.
• Нелинейное взаимодействие света и вещества со свободными электронами и плазмой .

Другие нелинейные процессы

• Оптический эффект Керра , показатель преломления, зависящий от интенсивности (a $\chi ^{(3)}$ эффект).
• Самофокусировка — эффект, обусловленный оптическим эффектом Керра (и, возможно, нелинейностями более высокого порядка), вызванный пространственным изменением интенсивности, создающим пространственное изменение показателя преломления.
• Синхронизация моделей линзы Керра (KLM), использование самофокусировки в качестве механизма синхронизации мод лазера.
• Фазовая автомодуляция (СЗМ), эффект, обусловленный оптическим эффектом Керра (и, возможно, нелинейностями более высокого порядка), вызванный временным изменением интенсивности, создающим временное изменение показателя преломления.
• Оптические солитоны , равновесное решение либо для оптического импульса (временной солитон), либо для пространственной моды (пространственный солитон), которое не меняется во время распространения из-за баланса между дисперсией и эффектом Керра (например, автофазовая модуляция для временной и самофокусирующейся для пространственных солитонов).
• Самодифракция, расщепление лучей в процессе многоволнового смешения с переносом потенциальной энергии.
• Перекрестно-фазовая модуляция (XPM), при которой одна длина волны света может влиять на фазу другой длины волны света посредством оптического эффекта Керра.
• Четырехволновое смешение (ЧВС) может возникнуть и из-за других нелинейностей.
• Генерация кроссполяризованных волн (XPW), а $\chi ^{(3)}$ эффект, при котором генерируется волна с вектором поляризации, перпендикулярным входному.
• Модуляционная нестабильность .
• Рамановское усиление
• Оптическое ОВФ .
• Вынужденное рассеяние Бриллюэна , взаимодействие фотонов с акустическими фононами.
• Многофотонное поглощение — одновременное поглощение двух и более фотонов с передачей энергии одному электрону.
• Множественная фотоионизация — почти одновременное удаление множества связанных электронов одним фотоном.
• Хаос в оптических системах .

Связанные процессы

В этих процессах среда имеет линейную реакцию на свет, но на свойства среды влияют другие причины:

• Эффект Поккельса , на показатель преломления влияет статическое электрическое поле; используется в электрооптических модуляторах .
• Акустооптика , на показатель преломления влияют акустические волны (ультразвук); используется в акустооптических модуляторах .
• Комбинационное рассеяние света , взаимодействие фотонов с оптическими фононами .

Параметрические процессы

Нелинейные эффекты делятся на две качественно разные категории: параметрические и непараметрические эффекты. Параметрическая нелинейность— это взаимодействие, при котором квантовое состояние нелинейного материала не изменяется за счет взаимодействия с оптическим полем. Вследствие этого процесс является «мгновенным». Энергия и импульс сохраняются в оптическом поле, что делает фазовый синхронизм важным и зависящим от поляризации.

Теория

Параметрические и «мгновенные» (т.е. материал должен быть без потерь и без дисперсии в соответствии с соотношениями Крамерса-Кронига ) нелинейные оптические явления, в которых оптические поля не слишком велики , могут быть описаны разложением в ряд Тейлора плотности диэлектрической поляризации ( электрический диполь момент на единицу объема) P ( t ) в момент времени t в терминах электрического поля E ( t ):

$\mathbf {P} (t)=\varepsilon _{0}\left(\chi ^{(1)}\mathbf {E} (t)+\chi ^{(2)}\mathbf {E} ^{2}(t)+\chi ^{(3)}\mathbf {E} ^{3}(t)+\ldots \right),$

где коэффициенты χ ^{( н )} – среды n -го порядка восприимчивости , и наличие такого члена обычно называют нелинейностью n -го порядка. Обратите внимание, что плотность поляризации P ( t ) и электрическое поле E ( t ) для простоты считаются скалярными. В общем, х ^{( н )} ( n + 1)-го ранга, представляет собой тензор представляющий как поляризационно -зависимый характер параметрического взаимодействия, так и симметрию (или отсутствие) нелинейного материала.

Волновое уравнение в нелинейном материале

Центральное место в изучении электромагнитных волн занимает волновое уравнение . Начиная с уравнений Максвелла в изотропном пространстве, не содержащем свободного заряда, можно показать, что

$\nabla \times \nabla \times \mathbf {E} +{\frac {n^{2}}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\mathbf {E} =-{\frac {1}{\varepsilon _{0}c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\mathbf {P} ^{\text{NL}},$

где Р ^{Нидерланды} — нелинейная часть плотности поляризации , а n — показатель преломления , который получается из линейного члена P. в

Обратите внимание, что обычно можно использовать векторное тождество

$\nabla \times \left(\nabla \times \mathbf {V} \right)=\nabla \left(\nabla \cdot \mathbf {V} \right)-\nabla ^{2}\mathbf {V}$

и закон Гаусса (при условии отсутствия свободных зарядов, $\rho _{\text{free}}=0$),

$\nabla \cdot \mathbf {D} =0,$

чтобы получить более знакомое волновое уравнение

$\nabla ^{2}\mathbf {E} -{\frac {n^{2}}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\mathbf {E} =\mathbf {0} .$

Для нелинейной среды закон Гаусса не означает, что тождество

$\nabla \cdot \mathbf {E} =0$

в целом справедливо даже для изотропной среды. Однако даже если этот член не равен 0, он часто пренебрежимо мал и поэтому на практике обычно игнорируется, что дает нам стандартное нелинейное волновое уравнение:

$\nabla ^{2}\mathbf {E} -{\frac {n^{2}}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\mathbf {E} ={\frac {1}{\varepsilon _{0}c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\mathbf {P} ^{\text{NL}}.$

Нелинейности как процесс смешения волн

Нелинейное волновое уравнение представляет собой неоднородное дифференциальное уравнение. Общее решение приходит в результате изучения обыкновенных дифференциальных уравнений и может быть получено с помощью функции Грина . Физически мы получаем нормальные электромагнитные волновые решения однородной части волнового уравнения:

$\nabla ^{2}\mathbf {E} -{\frac {n^{2}}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\mathbf {E} =\mathbf {0} ,$

и неоднородный член

${\frac {1}{\varepsilon _{0}c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\mathbf {P} ^{\text{NL}}$

действует как драйвер/источник электромагнитных волн. Одним из последствий этого является нелинейное взаимодействие, в результате которого энергия смешивается или связывается между разными частотами, что часто называют «волновым смешением».

В общем случае нелинейность n -го порядка приведет к ( n + 1)-волновому смешиванию. Например, если рассматривать только нелинейность второго порядка (трехволновое смешение), то поляризация P принимает вид

$\mathbf {P} ^{\text{NL}}=\varepsilon _{0}\chi ^{(2)}\mathbf {E} ^{2}(t).$

мы предположим, что E ( t ) состоит из двух компонентов на частотах и _ω1 ω2 , _Если мы можем записать E ( t ) как

$\mathbf {E} (t)=E_{1}\cos(\omega _{1}t)+E_{2}\cos(\omega _{2}t),$

и используя формулу Эйлера для преобразования в экспоненту,

$\mathbf {E} (t)={\frac {1}{2}}E_{1}e^{-i\omega _{1}t}+{\frac {1}{2}}E_{2}e^{-i\omega _{2}t}+{\text{c.c.}},$

где «cc» означает комплексно-сопряженный . Подстановка этого в выражение для P дает

${\begin{aligned}\mathbf {P} ^{\text{NL}}&=\varepsilon _{0}\chi ^{(2)}\mathbf {E} ^{2}(t)\\[3pt]&={\frac {\varepsilon _{0}}{4}}\chi ^{(2)}\left[{E_{1}}^{2}e^{-i2\omega _{1}t}+{E_{2}}^{2}e^{-i2\omega _{2}t}+2E_{1}E_{2}e^{-i(\omega _{1}+\omega _{2})t}+2E_{1}{E_{2}}^{*}e^{-i(\omega _{1}-\omega _{2})t}+\left(\left|E_{1}\right|^{2}+\left|E_{2}\right|^{2}\right)e^{0}+{\text{c.c.}}\right],\end{aligned}}$

который имеет частотные компоненты при 2 ω ₁ , 2 ω ₂ , ω ₁ + ω ₂ , ω ₁ − ω ₂ и 0. Эти процессы трехволнового смешивания соответствуют нелинейным эффектам, известным как генерация второй гармоники , генерация суммарной частоты . , генерация разностной частоты и оптическое выпрямление соответственно.

Примечание. Параметрическая генерация и усиление — это разновидность генерации разностной частоты, при которой нижняя частота одного из двух генерирующих полей значительно слабее (параметрическое усиление) или полностью отсутствует (параметрическая генерация). В последнем случае фундаментальная квантовомеханическая инициатором процесса является неопределенность в электрическом поле.

Фазовое согласование

Большинство прозрачных материалов, таких как показанное здесь стекло BK7 , имеют нормальную дисперсию : показатель преломления уменьшается монотонно в зависимости от длины волны (или увеличивается в зависимости от частоты). Это делает невозможным синхронизацию фаз в большинстве процессов смешения частот. Например, в ГСП не существует одновременного решения $\omega '=2\omega$ и $\mathbf {k} '=2\mathbf {k}$ в этих материалах. Двулучепреломляющие материалы позволяют избежать этой проблемы, поскольку имеют сразу два показателя преломления.

Вышеуказанное не учитывает позиционную зависимость электрических полей. В типичной ситуации электрические поля представляют собой бегущие волны, описываемые формулой

$E_{j}(\mathbf {x} ,t)=E_{j,0}e^{i(\mathbf {k} _{j}\cdot \mathbf {x} -\omega _{j}t)}+{\text{c.c.}}$

на позиции $\mathbf {x}$, с волновым вектором $\|\mathbf {k} _{j}\|=\mathbf {n} (\omega _{j})\omega _{j}/c$, где $c$ - скорость света в вакууме, а $\mathbf {n} (\omega _{j})$ - показатель преломления среды на угловой частоте $\omega _{j}$. Таким образом, поляризация второго порядка на угловой частоте $\omega _{3}=\omega _{1}+\omega _{2}$ является

$P^{(2)}(\mathbf {x} ,t)\propto E_{1}^{n_{1}}E_{2}^{n_{2}}e^{i[(\mathbf {k} _{1}+\mathbf {k} _{2})\cdot \mathbf {x} -\omega _{3}t]}+{\text{c.c.}}$

На каждой позиции $\mathbf {x}$ в нелинейной среде колеблющаяся поляризация второго порядка излучается с угловой частотой $\omega _{3}$ и соответствующий волновой вектор $\|\mathbf {k} _{3}\|=\mathbf {n} (\omega _{3})\omega _{3}/c$. Конструктивная интерференция и, следовательно, высокая интенсивность $\omega _{3}$ поле, произойдет только в том случае, если

${\vec {\mathbf {k} }}_{3}={\vec {\mathbf {k} }}_{1}+{\vec {\mathbf {k} }}_{2}.$

Приведенное выше уравнение известно как условие синхронизма . Обычно трехволновое смешение осуществляется в двулучепреломляющем кристаллическом материале, где показатель преломления зависит от поляризации и направления проходящего света. Поляризации полей и ориентация кристалла выбираются такими, чтобы выполнялось условие синхронизма. Этот метод фазового согласования называется настройкой угла. Обычно кристалл имеет три оси, одна или две из которых имеют показатель преломления, отличный от другого. Одноосные кристаллы, например, имеют одну предпочтительную ось, называемую необыкновенной (е) осью, тогда как две другие являются обычными осями (о) (см. Кристаллооптика ). Существует несколько схем выбора поляризаций для этого типа кристаллов. Если сигнал и холостой ход имеют одинаковую поляризацию, это называется «фазовым синхронизмом типа I», а если их поляризации перпендикулярны, это называется «фазовым синхронизмом типа II». Однако существуют и другие соглашения, которые дополнительно определяют, какая частота имеет какую поляризацию относительно оси кристалла. Эти типы перечислены ниже с учетом того, что длина волны сигнала короче длины волны холостого сигнала.

Типы фазового синхронизма

( $\lambda _{p}\leq \lambda _{s}\leq \lambda _{i}$)

Поляризации			Схема
Насос	Сигнал	Ленивец
и	тот	тот	Тип I
и	тот	и	Тип II (или IIA)
и	и	тот	Тип III (или IIB)
и	и	и	Тип IV
тот	тот	тот	Тип V (или тип 0, или «ноль»)
тот	тот	и	Тип VI (или IIB или IIIA)
тот	и	тот	Тип VII (или IIA или IIIB)
тот	и	и	Тип VIII (или I)

Наиболее распространенные нелинейные кристаллы являются отрицательными одноосными, что означает, что ось e имеет меньший показатель преломления, чем оси o . В таких кристаллах наиболее подходящими схемами синхронизма обычно являются типы I и -II. В положительных одноосных кристаллах больше подходят типы VII и VIII. Типы II и III по существу эквивалентны, за исключением того, что имена сигнала и холостого сигнала меняются местами, когда длина волны сигнала больше, чем у холостого. По этой причине их иногда называют IIA и IIB. Номера типов V – VIII встречаются реже, чем I, II и варианты.

Одним из нежелательных последствий настройки угла является то, что задействованные оптические частоты не распространяются коллинеарно друг другу. Это связано с тем, что необыкновенная волна, распространяющаяся через двулучепреломляющий кристалл, имеет вектор Пойнтинга , не параллельный вектору распространения. Это приведет к отклонению луча, что ограничивает эффективность нелинейного оптического преобразования. Два других метода фазового согласования позволяют избежать отклонения луча, заставляя все частоты распространяться под углом 90 ° по отношению к оптической оси кристалла. Эти методы называются температурной настройкой и квазисинхронизмом .

Температурная настройка используется, когда поляризация частоты накачки (лазера) ортогональна поляризации частоты сигнала и холостого сигнала. Двойное лучепреломление в некоторых кристаллах, в частности в ниобате лития, сильно зависит от температуры. Температура кристалла контролируется для достижения условий фазового синхронизма.

Другой метод — квазисинхронизм. В этом методе задействованные частоты не синхронизированы постоянно по фазе друг с другом, вместо этого ось кристалла переворачивается через регулярный интервал Λ, обычно длиной 15 микрометров. Поэтому такие кристаллы называются периодически поляризованными . Это приводит к тому, что поляризационный отклик кристалла смещается обратно по фазе с пучком накачки за счет обращения нелинейной восприимчивости. Это обеспечивает поток чистой положительной энергии от насоса на сигнальные и холостые частоты. В этом случае сам кристалл обеспечивает дополнительный волновой вектор k = 2π/Λ (и, следовательно, импульс) для выполнения условия синхронизма. Квазисинхронизм можно расширить до чирпированных решеток, чтобы получить большую полосу пропускания и сформировать импульс ГВГ, как это делается в ослепителе . ГВГ накачки и автофазовая модуляция (эмулируемая процессами второго порядка) сигнала и оптический параметрический усилитель могут быть интегрированы монолитно.

Смешение частот высшего порядка

Вышесказанное справедливо для $\chi ^{(2)}$ процессы. Его можно расширить для процессов, в которых $\chi ^{(3)}$ не равно нулю, что обычно верно для любой среды без каких-либо ограничений симметрии; в частности, резонансно усиленное смешение суммарных или разностных частот в газах часто используется для генерации экстремального или «вакуумного» ультрафиолетового света . В распространенных сценариях, таких как смешивание разбавленных газов, нелинейность слаба, поэтому световые лучи фокусируются, что, в отличие от приближения плоских волн, использованного выше, вносит пи-сдвиг фазы в каждый световой луч, усложняя требования к фазовому синхронизму. . Удобно, что смешивание разностных частот с $\chi ^{(3)}$ отменяет этот фокусный фазовый сдвиг и часто имеет почти самокомпенсируемое общее условие фазового синхронизма, что относительно упрощает настройку широкой длины волны по сравнению с генерацией суммарной частоты. В $\chi ^{(3)}$ все четыре частоты микшируются одновременно, в отличие от последовательного микширования через две $\chi ^{(2)}$ процессы.

Эффект Керра можно описать как $\chi ^{(3)}$ также. При высоких пиковых мощностях эффект Керра может вызвать филаментацию света в воздухе, при которой свет распространяется без дисперсии или расхождения в самогенерируемом волноводе. Даже при высоких интенсивностях ряд Тейлора , который привел к доминированию низших порядков, больше не сходится, и вместо этого используется модель, основанная на времени. Когда на атом благородного газа воздействует интенсивный лазерный импульс, напряженность электрического поля которого сравнима с кулоновским полем атома, самый внешний электрон может быть ионизирован из атома. После освобождения электрон может быть ускорен электрическим полем света, сначала удаляясь от иона, а затем обратно к нему, когда поле меняет направление. Затем электрон может рекомбинировать с ионом, высвобождая свою энергию в виде фотона. Свет излучается на каждом пике лазерного светового поля, который достаточно интенсивен и производит серию аттосекундных световых вспышек. Энергия фотонов, генерируемых этим процессом, может превышать 800-й порядок гармоники и достигать нескольких килоэВ . Это называется генерацией гармоник высокого порядка . Лазер должен быть линейно поляризованным, чтобы электрон возвращался в окрестности родительского иона. Генерация гармоник высокого порядка наблюдалась в струях благородных газов, ячейках и газонаполненных капиллярных волноводах.

Пример использования

Удвоение частоты

Одним из наиболее часто используемых процессов смешения частот является удвоение частоты или генерация второй гармоники. С помощью этой технологии выходная мощность Nd:YAG-лазеров с длиной волны 1064 нм или выходная мощность Ti:сапфировых лазеров с длиной волны 800 нм может быть преобразована в видимый свет с длинами волн 532 нм (зеленый) или 400 нм (фиолетовый) соответственно.

Практически удвоение частоты осуществляется путем помещения в лазерный луч нелинейной среды. Хотя существует множество типов нелинейных сред, наиболее распространенными средами являются кристаллы. Обычно используемые кристаллы: BBO ( β-борат бария ), KDP ( дигидрофосфат калия ), KTP ( титанилфосфат калия ) и ниобат лития . Эти кристаллы обладают необходимыми свойствами: сильное двойное лучепреломление (необходимое для получения фазового синхронизма, см. ниже), особая кристаллическая симметрия, прозрачность как для падающего лазерного света, так и для длины волны с удвоенной частотой, а также высокие пороги повреждения, что делает они устойчивы к воздействию лазерного света высокой интенсивности.

Оптическое ОВФ

Используя нелинейные оптические процессы, можно точно изменить направление распространения и изменение фазы луча света. Обратный луч называется сопряженным лучом, поэтому этот метод известен как оптическое обращение волнового фронта. (также называется обращением времени , обращением волнового фронта и существенно отличается от световозвращения ).

Устройство, создающее эффект ОВФ, известно как обращающее зеркало (ОВФ).

Принципы

Вихревой фотон (синий) с линейным импульсом $\mathbf {P} =\hbar \mathbf {k}$ и угловой момент $L=\pm \hbar \ell$ отражается от идеального ОВФ зеркала. Нормально для зеркала ${\vec {n}}$ , ось распространения ${\vec {z}}$. Отраженный фотон (пурпурный) имеет противоположный линейный импульс. $\mathbf {P} =-\hbar \mathbf {k}$ и угловой момент $L=\mp \hbar \ell$. Из-за законов сохранения зеркало ПК испытывает отдачу: вихревой фонон (оранжевый) с удвоенным линейным импульсом. $\mathbf {P} =2\hbar \mathbf {k}$ и угловой момент $L=\pm 2\hbar \ell$ возбужден в зеркале.

Можно интерпретировать оптическое ОВФ как аналог голографического процесса в реальном времени . В этом случае взаимодействующие лучи одновременно взаимодействуют в нелинейно-оптическом материале, образуя в материале динамическую голограмму (два из трех входных лучей) или дифракционную картину в реальном времени. Третий падающий луч дифрагирует на этой динамической голограмме и при этом считывает обращенную волну. По сути, все три падающих луча взаимодействуют (по сути) одновременно, образуя несколько голограмм в реальном времени, что приводит к набору дифрагированных выходных волн, которые фазируются как луч, «обращенный во времени». На языке нелинейной оптики взаимодействующие лучи приводят к нелинейной поляризации внутри материала, которая когерентно излучается, образуя обращенную волну.

Изменение волнового фронта означает полное изменение линейного момента и углового момента фотонов. Изменение углового момента означает изменение как состояния поляризации, так и орбитального углового момента. Изменение орбитального углового момента оптического вихря происходит за счет идеального совпадения винтовых фазовых профилей падающего и отраженного пучков. Оптическое ОВФ реализуется посредством вынужденного рассеяния Бриллюэна. четырехволновое смешивание, трехволновое смешивание, статические линейные голограммы и некоторые другие инструменты.

Сравнение обращенного зеркала с обычным зеркалом. При использовании обращенного зеркала изображение не деформируется при двукратном прохождении через аберрирующий элемент.

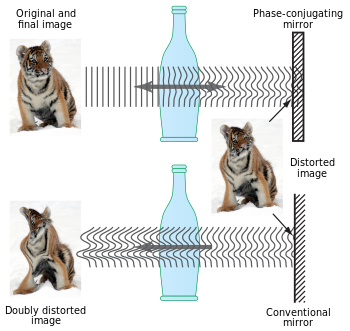
Наиболее распространенным способом создания оптического ОВФ является использование метода четырехволнового смешения, хотя также возможно использовать такие процессы, как вынужденное рассеяние Бриллюэна.

Техника четырехволнового смешивания

Для метода четырехволнового смешения мы можем описать четыре луча ( j = 1, 2, 3, 4) с электрическими полями:

$\Xi _{j}(\mathbf {x} ,t)={\frac {1}{2}}E_{j}(\mathbf {x} )e^{i\left(\omega _{j}t-\mathbf {k} \cdot \mathbf {x} \right)}+{\text{c.c.}},$

где E _j — амплитуды электрического поля. Ξ ₁ и Ξ ₂ известны как две волны накачки, причем Ξ ₃ является сигнальной волной, а Ξ ₄ является генерируемой сопряженной волной.

Если волны накачки и сигнальная волна наложены в среде с ненулевой χ ⁽³⁾ , это создает поле нелинейной поляризации:

$P_{\text{NL}}=\varepsilon _{0}\chi ^{(3)}(\Xi _{1}+\Xi _{2}+\Xi _{3})^{3},$

что приводит к генерации волн с частотами, заданными ω = ±ω ₁ ± ω ₂ ± ω _3, в дополнение к волнам генерации третьей гармоники с ω = 3ω ₁ , 3ω ₂ , 3ω ₃ .

Как и выше, условие синхронизма определяет, какая из этих волн является доминирующей. Выбирая такие условия, что ω = ω ₁ + ω ₂ − ω ₃ и k = k ₁ + k ₂ − k ₃ , это дает поле поляризации:

$P_{\omega }={\frac {1}{2}}\chi ^{(3)}\varepsilon _{0}E_{1}E_{2}E_{3}^{*}e^{i(\omega t-\mathbf {k} \cdot \mathbf {x} )}+{\text{c.c.}}$

Это порождающее поле для обращенного пучка Ξ ₄ . Его направление определяется выражением k ₄ = k ₁ + k ₂ − k ₃ , и поэтому, если два луча накачки распространяются встречно ( k ₁ = − k ₂ ), то сопряженный и сигнальный лучи распространяются в противоположных направлениях ( k ₄ = − к ₃ ). Это приводит к светоотражающему свойству эффекта.

Далее можно показать, что для среды с показателем преломления n и длиной взаимодействия лучей l амплитуда электрического поля сопряженного пучка аппроксимируется выражением

$E_{4}={\frac {i\omega l}{2nc}}\chi ^{(3)}E_{1}E_{2}E_{3}^{*},$

где с — скорость света. Если пучки накачки E ₁ и E ₂ представляют собой плоские (встречные) волны, то

$E_{4}(\mathbf {x} )\propto E_{3}^{*}(\mathbf {x} ),$

то есть амплитуда генерируемого луча является комплексно-сопряженной амплитудой сигнального луча. Поскольку мнимая часть амплитуды содержит фазу луча, это приводит к обращению фазового свойства эффекта.

Обратите внимание, что константа пропорциональности между сигнальным и сопряженным лучами может быть больше 1. Фактически это зеркало с коэффициентом отражения более 100%, создающим усиленное отражение. Энергия для этого поступает от двух лучей накачки, которые истощаются в результате этого процесса.

Частота сопряженной волны может отличаться от частоты сигнальной волны. Если волны накачки имеют частоту ω ₁ = ω ₂ = ω, а сигнальная волна имеет большую частоту, так что ω ₃ = ω + Δω, то сопряженная волна имеет частоту ω ₄ = ω − Δω. Это известно как переключение частоты .

Угловые и линейные моменты при оптическом ОВФ

Классическая картина

В классической электродинамике Максвелла обращающее зеркало выполняет обращение вектора Пойнтинга :

$\mathbf {S} _{\text{out}}(\mathbf {r} ,t)=-\mathbf {S} _{\text{in}}(\mathbf {r} ,t),$

(«in» означает падающее поле, «out» означает отраженное поле), где

$\mathbf {S} (\mathbf {r} ,t)=\epsilon _{0}c^{2}\mathbf {E} (\mathbf {r} ,t)\times \mathbf {B} (\mathbf {r} ,t),$

которая представляет собой линейную плотность импульса электромагнитного поля. Точно так же обращенная волна имеет противоположный вектор плотности углового момента $\mathbf {L} (\mathbf {r} ,t)=\mathbf {r} \times \mathbf {S} (\mathbf {r} ,t)$ относительно поля инцидента:

$\mathbf {L} _{\text{out}}(\mathbf {r} ,t)=-\mathbf {L} _{\text{in}}(\mathbf {r} ,t).$

Приведенные выше тождества действительны локально , т.е. в каждой точке пространства. $\mathbf {r}$ в данный момент $t$ для идеального ОВФ зеркала .

Квантовая картина

В квантовой электродинамике фотон с энергией $\hbar \omega$ также обладает линейным импульсом $\mathbf {P} =\hbar \mathbf {k}$ и угловой момент, проекция которого на ось распространения равна $L_{\mathbf {z} }=\pm \hbar \ell$, где $\ell$ — топологический заряд фотона, или число витков, $\mathbf {z}$ — ось распространения. Проекция углового момента на ось распространения имеет дискретные значения $\pm \hbar \ell$.

В квантовой электродинамике интерпретация ОВФ значительно проще по сравнению с классической электродинамикой . Фотон, отраженный от ОВФ-зеркала (наружу), имеет противоположные направления линейного и углового моментов по отношению к падающему фотону (внутри):

${\begin{aligned}\mathbf {P} _{\text{out}}&=-\hbar \mathbf {k} =-\mathbf {P} _{\text{in}}=\hbar \mathbf {k} ,\\{L_{\mathbf {z} }}_{\text{out}}&=-\hbar \ell =-{L_{\mathbf {z} }}_{\text{in}}=\hbar \ell .\end{aligned}}$

Формирование нелинейного оптического рисунка

Оптические поля, передаваемые через нелинейные среды Керра, также могут отображать формирование структуры из-за того, что нелинейная среда усиливает пространственный и временной шум. Этот эффект называется нестабильностью оптической модуляции . Это наблюдалось как в фоторефракционной, так и в фотонные решетки, а также фотореактивные системы. В последнем случае оптическая нелинейность обеспечивается за счет увеличения показателя преломления, вызванного реакцией. Примерами формирования узоров являются пространственные солитоны и вихревые решетки в рамках нелинейного уравнения Шрёдингера .

Молекулярная нелинейная оптика

Ранние исследования нелинейной оптики и материалов были сосредоточены на неорганических твердых телах. С развитием нелинейной оптики были исследованы молекулярно-оптические свойства, образовавшие молекулярную нелинейную оптику. Традиционные подходы, используемые в прошлом для усиления нелинейностей, включают расширение π-систем хромофора, корректировку изменения длины связей, индуцирование внутримолекулярного переноса заряда, расширение сопряжения в 2D и разработку мультиполярных распределений заряда. В последнее время было предложено множество новых направлений повышения нелинейности и манипулирования светом, в том числе скрученные хромофоры, сочетание богатой плотности состояний с чередованием связей, микроскопическое каскадирование нелинейности второго порядка и т. д. Благодаря выдающимся преимуществам молекулярная нелинейная оптика нашла широкое применение. в области биофотоники, включая биовизуализацию, фототерапия, биосенсорство, и т. д.

Соединение объемных свойств с микроскопическими свойствами

Молекулярная нелинейная оптика связывает оптические свойства объемного вещества с их микроскопическими молекулярными свойствами. Так же, как поляризуемость можно описать как разложение в ряд Тейлора , можно разложить индуцированный дипольный момент по степеням электрического поля: ${\boldsymbol {\mu }}={\boldsymbol {\mu _{0}}}+\alpha \cdot {\boldsymbol {\mathrm {E} }}+{\frac {1}{2}}\beta :{\boldsymbol {\mathrm {E} }}{\boldsymbol {\mathrm {E} }}$, где µ — поляризуемость, α — первая гиперполяризуемость , β — вторая гиперполяризуемость и так далее.

Новые нелинейные медиа

Некоторые молекулярные материалы имеют возможность оптимизировать оптическую нелинейность на микроскопическом и объемном уровнях. Из-за делокализации электронов в π-связях электроны легче реагируют на приложенные оптические поля и имеют тенденцию давать более сильные линейные и нелинейные оптические отклики, чем электроны в одинарных (𝜎) связях. В этих системах линейный отклик масштабируется с длиной сопряженной системы Пи, а нелинейный отклик масштабируется еще быстрее.

Хромофор зеленого флуоресцентного белка (GFP) п-гидроксибензилиденимидазолинон (HBDI), используемый в нелинейной биовизуализации, является примером пи-конъюгированного донорно-акцепторного (D-π-A) хромофора.

Одним из многих применений молекулярной нелинейной оптики является использование в нелинейной биовизуализации. Эти нелинейные материалы, такие как многофотонные хромофоры , используются в качестве биомаркеров в двухфотонной спектроскопии, в которой затухание интенсивности падающего света при его прохождении через образец записывается как ${-dI \over dx}={N\delta I^{2} \over \hbar \omega }$.

где N — количество частиц в единице объема, I — интенсивность света, а δ — сечение двухфотонного поглощения . Результирующий сигнал принимает форму лоренцевой линии с поперечным сечением, пропорциональным разнице дипольных моментов основного и конечного состояний.

Подобные высокосопряженные хромофоры с сильными донорно-акцепторными характеристиками используются из-за их большой разницы в дипольных моментах, и в настоящее время предпринимаются усилия по расширению их пи-сопряженных систем для улучшения их нелинейных оптических свойств.

Распространенные материалы, генерирующие вторую гармонику (ГВГ)

См. Также: Генерация второй гармоники.

Темно-красный селенид галлия в нерасфасованном виде.

В порядке длины волны накачки:

• 800 нм: ББО
• 806 нм: иодат лития (LiIO ₃ ).
• 860 нм: ниобат калия (KNbO ₃ )
• 980 нм: KNbO ₃
• 1064 нм: монофосфат калия (KH ₂ PO ₄ , KDP), триборат лития (LBO) и β-борат бария (BBO)
• 1300 нм: селенид галлия (GaSe)
• 1319 нм: KNbO ₃ , BBO, KDP, титанилфосфат калия (KTP), ниобат лития (LiNbO ₃ ), LiIO ₃ и дигидрофосфат аммония (ADP).
• 1550 нм: титанилфосфат калия (КТП), ниобат лития (LiNbO ₃ )

См. также

• Модель Борна – Инфельда
• Распространение нити
• Категория: Нелинейно-оптические материалы

Дальнейшее чтение

• Энциклопедия лазерной физики и технологий. Архивировано 3 июня 2009 г. в Wayback Machine , с содержанием по нелинейной оптике, автор Рюдигер Пашотта.
• Интуитивное объяснение ОВФ. Архивировано 8 ноября 2007 г. в Wayback Machine.
• SNLO - Программное обеспечение для проектирования нелинейной оптики, заархивировано 7 июля 2011 г. на Wayback Machine.
• Пленарная презентация Роберта Бойда: Квантовая нелинейная оптика: нелинейная оптика встречает квантовый мир. Архивировано 17 марта 2016 г. в отделе новостей Wayback Machine SPIE.
• Бойд, RW (2020). Нелинейная оптика (4-е изд.). Академия. ISBN  978-0-12-811003-4 .