Покрытие пространства

В топологии покрытие локально или покрывающая проекция — это карта между топологическими пространствами , которая интуитивно действует как проекция множества копий пространства на себя. В частности, накрытия представляют собой специальные виды локальных гомеоморфизмов . Если представляет собой покрытие, называется пространством или покрытием покрывающим , и Говорят, что это основа покрытия или просто основа . Злоупотребляя терминологией , и можно назвать покрывающими пространствами иногда также . Поскольку накрытия являются локальными гомеоморфизмами, накрывающее пространство представляет собой особый вид этального пространства .
Накрывающие пространства впервые возникли в контексте комплексного анализа (в частности, техники аналитического продолжения ), где они были введены Риманом как области, на которых естественно многозначные комплексные функции становятся однозначными. Эти пространства теперь называются римановыми поверхностями . [1] : 10
Покрывающие пространства являются важным инструментом в нескольких областях математики. В современной геометрии накрывающие пространства (или разветвленные накрытия , имеющие несколько более слабые условия) используются при построении многообразий , орбифолдов и морфизмов между ними. В алгебраической топологии накрывающие пространства тесно связаны с фундаментальной группой : во-первых, поскольку все покрытия обладают свойством гомотопического подъема , накрывающие пространства являются важным инструментом при вычислении гомотопических групп . Стандартный пример в этом духе — вычисление фундаментальной группы окружности посредством покрытия к (см. ниже ). [2] : 29 При определенных условиях накрывающие пространства также обнаруживают соответствие Галуа с подгруппами фундаментальной группы.
Определение [ править ]
Позволять быть топологическим пространством. Покрытие представляет собой непрерывную карту
такой, что для каждого существует открытое соседство из и дискретное пространство такой, что и является гомеоморфизмом для любого .Открытые наборы называются листами , которые определяются однозначно с точностью до гомеоморфизма, если подключен . [2] : 56 Для каждого дискретный набор называется волокном . Если связно, можно показать, что сюръективен , мощность а одинаково для всех ; эта величина называется степенью покрытия. Если линейно связна , то накрытие называется линейно-связным покрытием . Это определение эквивалентно утверждению, что является локально тривиальным расслоением Fiber .
Некоторые авторы также требуют, чтобы быть сюръективным в том случае, если не подключен. [3]
Примеры [ править ]
- Для любого топологического пространства , карта личности является покрытием. Аналогично для любого дискретного пространства проекция принимая является покрытием. Покрытия этого типа называются тривиальными покрытиями ; если имеет конечное число (скажем ) элементов, покрытие называется тривиальным листовое покрытие - .

- Карта с является покрытием единичной окружности . Основа покрытия и площадь покрытия . Для любой точки такой, что , набор это открытый район . Прообраз под является
- и листы покрытия для Волокно является
- Еще одним покрытием единичного круга является карта с для некоторых Для открытого соседства из , у одного есть:
- .
- Отображение, являющееся локальным гомеоморфизмом , но не покрывающее единичную окружность, называется с . Имеется лист открытой окрестности , который не отображается гомеоморфно на .
Свойства [ править ]
Локальный гомеоморфизм
Поскольку покрытие отображает каждое из непересекающихся открытых множеств гомеоморфно на это локальный гомеоморфизм, т.е. является непрерывным отображением и для каждого существует открытое соседство из , такой, что является гомеоморфизмом.
Отсюда следует, что накрывающее пространство и базовое пространство локально имеют одни и те же свойства.
- Если — связное и неориентируемое многообразие , то существует накрытие степени , в результате чего является связным и ориентируемым многообразием. [2] : 234
- Если — связная группа Ли , то существует накрытие который также является гомоморфизмом группы Ли и является группой Ли. [4] : 174
- Если является графом , то для покрытия следует что это тоже график. [2] : 85
- Если — связное многообразие , то существует накрытие , в результате чего является связным и односвязным многообразием. [5] : 32
- Если — связная риманова поверхность , то существует накрытие которое также является голоморфным отображением [5] : 22 и — связная и односвязная риманова поверхность. [5] : 32
Факторизация [ править ]
Позволять и быть линейно-связными, локально линейно-связными пространствами и и — непрерывные отображения, такие, что диаграмма
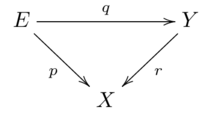
ездит на работу.
- Если и являются покрытиями, так что .
- Если и являются покрытиями, так что . [6] : 485
Продукт покрытий [ править ]
Позволять и быть топологическими пространствами и и быть покрытиями, тогда с является покрытием. [6] : 339 Однако покрытия не все в этой форме вообще.
Эквивалентность покрытий [ править ]
Позволять быть топологическим пространством и и быть покрытиями. Оба накрытия называются эквивалентными , если существует гомеоморфизм , такой, что диаграмма

ездит на работу. Если такой гомеоморфизм существует, то накрывающие пространства называются и изоморфный .
Подъемное имущество [ править ]
Все покрытия обладают подъемным свойством , т.е.:
Позволять быть единичным интервалом и быть покрытием. Позволять быть непрерывным отображением и быть лифтом , т. е. непрерывное отображение такое, что . Тогда существует однозначно определенное непрерывное отображение для чего и что такое лифт , то есть . [2] : 60
Если является линейно-связным пространством, то для следует, что карта это подъем пути в и для это подъем гомотопии путей в .
Как следствие, можно показать, что фундаментальная группа единичной окружности — бесконечная циклическая группа , порожденная гомотопическими классами петли с . [2] : 29
Позволять быть пространством, связанным между собой и быть связным покрытием. Позволять любые две точки, соединенные путем , то есть и . Позволять быть уникальным лифтом , то карта
- с
является биективным . [2] : 69
Если представляет собой пространство, связанное путями, и связное накрытие, то индуцированный групповой гомоморфизм
- с ,
инъективна и подгруппа из состоит из гомотопических классов петель в , лифты которого являются петлями в . [2] : 61
Разветвленное покрытие [ править ]
Определения [ править ]
поверхностей Голоморфные отображения римановых
Позволять и — римановы поверхности , т.е. одномерные комплексные многообразия , и пусть быть непрерывным отображением. голоморфен в точке , если для любых графиков из и из , с , карта является голоморфным .
Если вообще голоморфен , мы говорим голоморфен .
Карта называется локальным выражением в .
Если — непостоянное голоморфное отображение между компактными римановыми поверхностями , то является сюръективной и открытой картой , [5] : 11 т.е. для каждого открытого набора изображение также открыт.
Точка ветвления и точка ветвления [ править ]
Позволять — непостоянное голоморфное отображение компактных римановых поверхностей. Для каждого существуют диаграммы для и и существует однозначно определенное , такой, что локальное выражение из в имеет форму . [5] : 10 Число называется ветвления индексом в и точка называется точкой ветвления, если . Если для , затем является неразветвленным . Точка изображения точки ветвления называется точкой ветвления.
Степень голоморфного отображения [ править ]
Позволять — непостоянное голоморфное отображение компактных римановых поверхностей. Степень из — мощность слоя неразветвленной точки , то есть .
Это число вполне определено, так как для каждого волокно дискретен [5] : 20 и для любых двух неразветвленных точек , это:
Его можно рассчитать по:
- [5] : 29
Разветвленное покрытие [ править ]
Определение [ править ]
Непрерывная карта называется разветвленным покрытием , если существует замкнутое множество с плотным дополнением , такой, что является покрытием.
Примеры [ править ]
- Позволять и , затем с является разветвленным накрытием степени , где по является точкой ветвления.
- Каждое непостоянное голоморфное отображение компактных римановых поверхностей. степени является разветвленным накрытием степени .
Универсальное покрытие [ править ]
Определение [ править ]
Позволять быть односвязным накрытием. Если — другое односвязное накрытие, то существует однозначно определенный гомеоморфизм , такой, что диаграмма

ездит на работу. [6] : 482
Это означает, что с точностью до эквивалентности определена однозначно и в силу этого универсального свойства называется универсальным накрытием пространства .
Существование [ править ]
Универсальное покрытие не всегда существует, но его существование гарантируют следующие свойства:
Позволять быть связным, локально односвязным топологическим пространством; тогда существует универсальное накрытие .
определяется как и к . [2] : 64
Топология на строится следующим образом: Пусть быть путем с . Позволять быть односвязной окрестностью конечной точки , то для каждого пути внутри от к однозначно определены с точностью до гомотопии . Теперь рассмотрим , затем с является биекцией и может быть оснащен окончательной топологией .
Основная группа действует свободно через на и с является гомеоморфизмом, т.е. .
Примеры [ править ]

- с — универсальное покрытие единичной окружности .
- с является универсальным покрытием проективного пространства для .
- с является универсальным накрытием унитарной группы . [7] : 5, Теорема 1
- С , то фактор-отображение является универсальным покрытием .
- Топологическое пространство, не имеющее универсального покрытия, — это гавайская серьга : Можно показать, что никакая окрестность начала координат просто связано. [6] : 487, Пример 1
G-покрытия [ править ]
Пусть G — дискретная группа, в топологическом пространстве X. действующая Это означает, что каждый элемент g группы G связан с гомеоморфизмом H g группы X на самого себя таким образом, что H g h всегда равен H g ∘ H h для любых двух элементов g и h группы G . (Иными словами, групповое действие группы G на пространстве X — это не что иное, как групповой гомоморфизм группы G в группу Homeo( X ) самогомеоморфизмов X ). Естественно задаться вопросом, при каких условиях проекция из X в пространство орбит X / G является накрывающим отображением. Это не всегда так, поскольку действие может иметь фиксированные точки. Примером этого является циклическая группа порядка 2, действующая на произведение X × X действием скручивания, где неединичный элемент действует по принципу ( x , y ) ↦ ( y , x ) . Таким образом, изучение связи между фундаментальными группами X и X / G не так просто.
Однако группа G действительно действует на фундаментальный группоид X орбитальные , и поэтому исследование лучше всего проводить, рассматривая группы, действующие на группоиды, и соответствующие группоиды . Теория этого изложена в главе 11 книги «Топология и группоиды», упомянутой ниже. Основной результат состоит в том, что для разрывных действий группы G на хаусдорфовом пространстве X , допускающем универсальное накрытие, фундаментальный группоид пространства орбит X / G изоморфен орбитальному группоиду фундаментального группоида X , т. е. фактор этого группоида действием группы G . Это приводит к явным вычислениям, например, фундаментальной группы симметрического квадрата пространства.
Трансформация колоды [ править ]
Определение [ править ]
Позволять быть покрытием. — Преобразование колоды это гомеоморфизм. , такой, что диаграмма непрерывных отображений
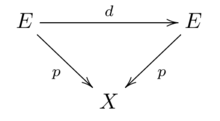
ездит на работу. Вместе с составом карт набор трансформации колоды образует группу , что то же самое, что .
Теперь предположим является покрывающей картой и (и, следовательно, также ) подключен и подключен локально. Действие на каждом слое транзитивно . Если это действие свободно на каком-то слое, то оно свободно на всех слоях, и накрытие мы называем регулярным (или нормальным , или Галуа ). Каждое такое регулярное покрытие является принципалом -расслоение , где рассматривается как дискретная топологическая группа.
Каждый универсальный чехол является регулярным, причем группа преобразований колоды изоморфна фундаментальной группе .
Примеры [ править ]
- Позволять быть прикрытием для некоторых , то карта это трансформация колоды и .
- Позволять быть прикрытием , то карта с это трансформация колоды и .
- В качестве еще одного важного примера рассмотрим сложная плоскость и комплексная плоскость минус начало координат. Тогда карта с это обычный чехол. Преобразования колоды представляют собой умножения с Таким образом, корни -й степени из единицы и группа преобразований колоды изоморфны циклической группе. . Аналогично, карта с это универсальный чехол.
Свойства [ править ]
Позволять быть пространством, связанным между собой и быть связным покрытием. С момента трансформации колоды является биективным , он переставляет элементы слоя с и однозначно определяется тем, куда он отправляет одну точку. В частности, только тождественная карта фиксирует точку в волокне. [2] : 70 Благодаря этому свойству каждое преобразование колоды определяет групповое действие над , то есть пусть быть открытым районом и открытый район , затем это групповое действие .
Обычные покрытия [ править ]
Определение [ править ]
Покрытие называется нормальным, если . Это означает, что для каждого и любые два существует трансформация колоды , такой, что .
Свойства [ править ]
Позволять быть пространством, связанным между собой и быть связным покрытием. Позволять быть подгруппой , затем это нормальное покрытие тогда и только тогда является нормальной подгруппой .
Если является обычным покрытием и , затем .
Если является линейно-связным покрытием и , затем , в результате чего является нормализатором . [2] : 71
Позволять быть топологическим пространством. Группа действует прерывисто на , если каждый имеет открытое окружение с , такой, что для каждого с у одного есть .
Если группа действует разрывно в топологическом пространстве , то фактор-отображение с это обычное покрытие. [2] : 72 Настоящим является факторпространством и — орбита действия группы.
Примеры [ править ]
- Покрытие с это нормальное покрытие для каждого .
- Всякое односвязное накрытие является нормальным накрытием.
Расчет [ править ]
Позволять — группа, действующая разрывно в топологическом пространстве. и пусть быть обычным покрытием.
- Если связен по путям, то . [2] : 72
- Если просто связен, то . [2] : 71
Примеры [ править ]
- Позволять . Антиподальная карта с генерирует вместе с составом карт группу и вызывает групповое действие , который действует разрывно на . Из-за отсюда следует, что факторотображение является нормальным покрытием и для универсальное покрытие, следовательно для .
- Позволять — специальная ортогональная группа , то отображение является нормальным покрытием и из-за , это универсальное накрытие, следовательно .
- С групповым действием из на , в результате чего это полупрямой продукт , получим универсальное накрытие из бутылки Клейна , следовательно .
- Позволять быть тором , вложенным в . Тогда получается гомеоморфизм , что индуцирует разрывное групповое действие , в результате чего . Отсюда следует, что карта является нормальным покрытием бутылки Клейна, следовательно .
- Позволять быть встроен в . Поскольку групповое действие носит прерывистый характер, при этом взаимнопросты карта , — универсальное покрытие хрусталикового пространства , следовательно .
Переписка Галуа [ править ]
Позволять — связное и локально односвязное пространство, то для каждой подгруппы существует линейно-связное накрытие с . [2] : 66
Позволять и — два линейно-связных покрытия, то они эквивалентны тогда и только тогда, когда подгруппы и сопряжены друг с другом. [6] : 482
Позволять — связное и локально односвязное пространство, то с точностью до эквивалентности покрытий существует биекция:
Для последовательности подгрупп получается последовательность накрытий . Для подгруппы с индексом , покрытие имеет степень .
Классификация [ править ]
Определения [ править ]
Категория покрытий [ править ]
Позволять быть топологическим пространством. Объекты категории это покрытия из и морфизмы между двумя накрытиями и представляют собой непрерывные карты , такой, что диаграмма

ездит на работу.
G-Set [ править ]
Позволять быть топологической группой . Категория — категория множеств, являющихся G-множествами . Морфизмы являются G-отображениями. между G-сетами. Они удовлетворяют условию для каждого .
Эквивалентность [ править ]
Позволять быть связным и локально односвязным пространством, и быть основной группой . С определяет, поднимая пути и оценивая в конечной точке подъема групповое действие на слое покрытия, функтор есть эквивалентность категорий . [2] : 68–70
Приложения [ править ]

Важное практическое применение покрывающих пространств происходит в диаграммах на SO(3) , группе вращения . Эта группа широко распространена в технике, поскольку трехмерное вращение широко используется в навигации , морской технике и аэрокосмической технике , а также во многих других областях. Топологически SO(3) — это реальное проективное пространство RP. 3 , с фундаментальной группой Z /2 и единственным (нетривиальным) накрывающим пространством гиперсферы S 3 , которая является группой Spin(3) и представлена единичными кватернионами . Таким образом, кватернионы являются предпочтительным методом представления пространственного вращения – см. кватернионы и пространственное вращение .
Однако часто желательно представлять вращение набором из трех чисел, известных как углы Эйлера (во многих вариантах), как потому, что это концептуально проще для тех, кто знаком с плоским вращением, так и потому, что можно построить комбинацию из трех подвесов для производить вращения в трех измерениях. Топологически это соответствует отображению 3-тора T 3 трех углов к реальному проективному пространству RP 3 вращений, и полученная карта имеет недостатки из-за того, что эта карта не может быть покрывающей картой. В частности, неспособность карты быть локальным гомеоморфизмом в определенных точках называется блокировкой карданного подвеса и демонстрируется в анимации справа — в некоторых точках (когда оси копланарны) ранг карты равен 2, а не 3, что означает, что из этой точки можно реализовать только два измерения вращения путем изменения углов. Это вызывает проблемы в приложениях и формализуется понятием покрывающего пространства.
См. также [ править ]
- Решетка Бете — универсальное покрытие графа Кэли.
- Граф покрытия , пространство покрытия неориентированного графа и его особый случай — двудольное двойное покрытие.
- Группа покрытия
- Связь Галуа
- Факторпространство (топология)
Литература [ править ]
- Хэтчер, Аллен (2002). Алгебраическая топология . Кембридж: Издательство Кембриджского университета. ISBN 0-521-79160-Х . OCLC 45420394 .
- Форстер, Отто (1981). Лекции по римановым поверхностям . Нью-Йорк. ISBN 0-387-90617-7 . OCLC 7596520 .
{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка ) - Манкрес, Джеймс Р. (2018). Топология . Нью-Йорк, штат Нью-Йорк. ISBN 978-0-13-468951-7 . ОСЛК 964502066 .
{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка ) - Кюнель, Вольфганг (2011). Матрицы и группы Ли. Геометрическое введение (на немецком языке). Висбаден: Vieweg+Teubner Verlag. дои : 10.1007/978-3-8348-9905-7 . ISBN 978-3-8348-9905-7 . OCLC 706962685 .
Ссылки [ править ]
- ^ Форстер, Отто (1981). «Глава 1: Покрытие пространств». Лекции по римановым поверхностям . ГТМ. Перевод Брюса Джиллиана. Нью-Йорк: Спрингер. ISBN 9781461259633 .
- ^ Jump up to: Перейти обратно: а б с д и ж г час я дж к л м н тот п Хэтчер, Аллен (2001). Алгебраическая топология . Кембридж: Кембриджский университет. Нажимать. ISBN 0-521-79160-Х .
- ^ Роуленд, Тодд. «Карта покрытия». Из MathWorld — веб-ресурса Wolfram, созданного Эриком В. Вайсштейном. https://mathworld.wolfram.com/CoveringMap.html
- ^ Кюнель, Вольфганг (6 декабря 2010 г.). Матрицы и группы Ли . Штутгарт: Springer Fachmedien Wiesbaden GmbH. ISBN 978-3-8348-9905-7 .
- ^ Jump up to: Перейти обратно: а б с д и ж г Форстер, Отто (1991). Лекции по римановым поверхностям . Мюнхен: Springer Berlin. ISBN 978-3-540-90617-9 .
- ^ Jump up to: Перейти обратно: а б с д и Манкрес, Джеймс (2000). Топология . Река Аппер-Сэддл, Нью-Джерси: ISBN Prentice Hall, Inc. 978-0-13-468951-7 .
- ^ Агилар, Марсело Альберто; Соколовский, Мигель (23 ноября 1999 г.). «Универсальная накрывающая группа U (n) и проективные представления». Международный журнал теоретической физики . 39 (4). Springer US (опубликовано в апреле 2000 г.): 997–1013. arXiv : math-ph/9911028 . Бибкод : 1999math.ph..11028A . дои : 10.1023/А:1003694206391 . S2CID 18686364 .
























![{\displaystyle Y=[0,1]\times \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b566709fb62d0c99d75506726ea4f22fc3f98078)
![{\displaystyle X=[0,1]\times S^{1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ecfebcfe87fcb8d16f87d9f6dfecca71bf16af1)
































































![{\displaystyle p_ {\#}([\gamma])=[p\circ \gamma ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0da1f32b69d662c4ca704e03c7f6665cc4c2bbe)







































![{\displaystyle p([\gamma ]):=\gamma (1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aeee3b9f2b1a930620d001de56151981af9f4210)








![{\displaystyle p([\gamma .\sigma _{y}])=\gamma .\sigma _{y}(1)=y}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6bb60eab8680bfa053e679348dc30132cb28713)



![{\displaystyle ([\gamma ],[{\tilde {x}}])\mapsto [\gamma .{\tilde {x}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0fa9846bd74343d9821f1568af6a33b418496a42)

![{\displaystyle \psi ([\Gamma {\tilde {x}}])={\tilde {x}}(1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa3e15841c84e4fbc78e76e0794e15bf868f1877)


![{\displaystyle p(x)=[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24b8773dff8ad19fc5a8f33134a4da367b04fc0c)















































































![{\displaystyle S^{3}\times \mathbb {Z/pZ} \rightarrow S^{3}:((z_{1},z_{2}),[k])\mapsto (e^{2\ пи ik/p}z_{1},e^{2\pi ikq/p}z_{2})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72ebd3752fc18f7e53cc92a583d04ac1b95a75ac)















![{\displaystyle \displaystyle [\pi _{1}(X):H]=d}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b9159dd8a0e29ba795fe865ddb5140ae95fd675)








