Упражнение (математика)

Математическое упражнение — это обычное применение алгебры или другой математики для решения поставленной задачи. Учителя математики предлагают математические упражнения для развития навыков своих учеников. Первые упражнения касаются сложения , вычитания , умножения и деления целых чисел . Обширные курсы упражнений в школе распространяют такую ​​арифметику на рациональные числа . Различные подходы к геометрии основываются на упражнениях на взаимоотношениях углов , отрезков и треугольников . Тема тригонометрии во многом основана на тригонометрических тождествах . математике часто зависят от функций действительной В колледжах упражнения по переменной или применения теорем . Стандартные упражнения по математическому анализу включают в себя нахождение производных и интегралов заданных функций.

Обычно преподаватели готовят студентов на отработанных примерах : излагается упражнение, затем дается примерный ответ. Часто перед тем, как учащиеся будут готовы выполнить упражнения самостоятельно, демонстрируются несколько проработанных примеров. Некоторые тексты, например, в «Очерках» Шаума , сосредоточены на проработанных примерах, а не на теоретическом рассмотрении математической темы.

Обзор

По мнению Льва Выготского , соответствующие упражнения лежат в зоне, где учащиеся могут выполнить задание под руководством.

В начальной школе учащиеся начинают с однозначными числами арифметических упражнений с . Позже большинство упражнений включают в себя как минимум две цифры. упражнение в элементарной алгебре требует факторизации многочленов . Обычное Еще одно упражнение — завершение квадрата многочленом квадратным . Искусственно созданная словесная задача — это жанр упражнений, призванный поддерживать актуальность математики. Стивен Ликок описал этот тип:

Изучающий арифметику, освоивший первые четыре правила своего искусства и успешно решающий суммы и дроби , сталкивается с непрерывным пространством вопросов, известных как задачи. Это короткие рассказы о приключениях и промышленности с опущенным концом, которые, хотя и обнаруживают сильное семейное сходство, не лишены определенного элемента романтики.

Различие между упражнением и математической задачей было проведено Аланом Х. Шенфельдом :

Студенты должны освоить соответствующий предмет, и для этого подходят упражнения. Но если зубрежка — единственные проблемы, с которыми ученики сталкиваются на уроках, мы оказываем им плохую услугу.

Он выступал за постановку задач:

Под «реальными задачами»… я имею в виду математические задачи, которые бросают честный вызов ученику и над которыми ему необходимо поработать, чтобы получить решение.

Аналогичное мнение выразил Марвин Биттингер, когда готовил второе издание. из его учебника:

В ответ на комментарии пользователей авторы добавили упражнения, которые требуют от ученика чего-то иного, чем понимание непосредственных целей урока, но не обязательно являются очень сложными.

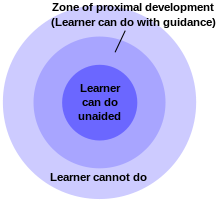
Зона ближайшего развития для каждого учащегося или группы учащихся устанавливает упражнения на уровень сложности, который бросает им вызов, но не расстраивает его.

Некоторые комментарии в предисловии к учебнику по математическому анализу. показать центральное место упражнений в книге:

Упражнения составляют около четверти текста – на наш взгляд, это самая важная часть текста. ... Дополнительные упражнения в конце каждой главы дополняют другие наборы упражнений и содержат совокупные упражнения, требующие навыков из предыдущих глав.

Этот текст включает в себя «Функции и графики в приложениях» (гл. 0.6), представляющие собой четырнадцать страниц подготовки к решению текстовых задач.

Авторы книги о конечных полях свободно выбирали свои упражнения:

Чтобы повысить привлекательность этой книги как учебника , мы включили проработанные примеры в соответствующие места текста и включили списки упражнений для глав 1–9. Эти упражнения варьируются от рутинных задач до альтернативных доказательств ключевых теорем. , но содержащий также материал, выходящий за рамки того, что рассмотрено в тексте.

Дж. К. Максвелл объяснил, как упражнения облегчают доступ к языку математики :

Как математики, мы совершаем определенные мыслительные операции над символами числа или количества и, переходя шаг за шагом от более простых операций к более сложным, мы имеем возможность выражать одно и то же во многих различных формах. Эквивалентность этих различных форм, хотя и является необходимым следствием самоочевидных аксиом, не всегда, по нашему мнению, является самоочевидной; но математик, который в результате долгой практики познакомился со многими из этих форм и стал экспертом в процессах, ведущих от одной к другой, часто может преобразовать одно сбивающее с толку выражение в другое, объясняющее его значение на более понятном языке.

Отдельные преподаватели различных колледжей используют упражнения в рамках своих курсов математики. Исследуя решение проблем в университетах, Шенфельд отметил:

Предложения старших классов по специальностям математики, где по большей части студенты работали над сборниками задач, составленными их отдельными преподавателями. На таких курсах упор делался на обучение на практике, без попыток преподавать конкретную эвристику: студенты решали множество задач, потому что (согласно неявной модели обучения, лежащей в основе таких курсов) именно так можно добиться успехов в математике.

Такие сборники упражнений могут являться собственностью инструктора и его учреждения. В качестве примера ценности комплексов упражнений рассмотрим достижения Тору Кумона и его метода Кумона . В его программе ученик не приступает к освоению каждого уровня упражнений. В Российской математической школе учащиеся начинают решать многоэтапные задачи уже в первом классе, учатся опираться на предыдущие результаты для продвижения к решению.

В 1960-е годы сборники математических упражнений были переведены с русского языка и изданы издательством WH Freeman and Company : The Professor Olympiad Task Book (1962), Проблемы высшей алгебры (1965), и проблемы дифференциальных уравнений (1963).

История

В Китае с древних времен для обозначения чисел использовались счетные палочки , а арифметика выполнялась с помощью палочного исчисления , а затем и суаньпаня . Книга «Числа и вычисления» и «Девять глав математического искусства» включают упражнения, являющиеся образцами линейной алгебры .

Примерно в 980 году Аль-Сиджи написал книгу « Способы облегчения вывода геометрических фигур» , которая была переведена и опубликована Яном Хогендейком в 1996 году.

Сборник упражнений на арабском языке был переведен на испанский язык под названием Compendio de Algebra de Abenbéder и опубликован в журнале Nature .

Роберт Рекорд впервые опубликовал «Землю искусств» в 1543 году.

Во-первых, это была почти вся экспозиция с очень небольшим количеством упражнений. Последние приобрели известность в восемнадцатом и девятнадцатом веках. Для сравнения мы могли бы взглянуть на другой бестселлер, а именно « Помощник наставника» Walkingame , впервые опубликованный в 1751 году, 70 процентов которого было посвящено упражнениям, по сравнению с примерно 1 процентом у Recorde. Включение упражнений было одним из наиболее значительных последующих изменений в учебниках по арифметике и происходило параллельно с развитием образования, поскольку учителя начали использовать учебники в качестве источников упражнений. Рекорд писал в основном для тех, кто учился сам, для ученых, которым некому было проверять ответы на упражнения.

В Европе до 1900 года наука графической перспективы легла в основу геометрических упражнений. Например, в 1719 году Брук Тейлор написал в «Новых принципах линейной перспективы»

[Читатель] получит гораздо больше удовольствия, наблюдая, насколько обширны эти Принципы, применяя их к конкретным случаям, которые он сам придумает, пока упражняется в этом Искусстве...

Тейлор продолжил

...ибо истинный и лучший способ изучить любое Искусство - это не видеть множество примеров, выполненных другим человеком; но сначала необходимо овладеть его Принципами, а затем познакомить их, упражняясь в Практике.

Использование досок для письма в школах стало первым форматом упражнений. Рост программ упражнений последовал за введением письменных экзаменов и обучения с помощью ручки и бумаги.

Феликс Кляйн описал подготовку к вступительным экзаменам в Политехническую школу как

...курс «Специальной математики». Это чрезвычайно сильная концентрация математического образования – до 16 часов в неделю – при которой элементарная аналитическая геометрия и механика, а в последнее время и исчисление бесконечно малых, тщательно изучаются и посредством множества упражнений превращаются в надежно освоенный инструмент.

Сильвестр Лакруа был талантливым учителем и пропагандистом. В его книге по начертательной геометрии используются разделы с надписью «Проблема», чтобы улучшить понимание читателя. В 1816 году он написал «Очерки по преподаванию вообще и по преподаванию математики в частности», в которых подчеркивалась необходимость упражнений и проверок:

Экзаменатор, вынужденный в краткосрочной перспективе умножить свои вопросы настолько, чтобы охватить задаваемые им предметы, к большей части преподаваемого материала, не может быть менее тщательным, поскольку, если, сокращенно, он откладывает приложения в сторону, он Таким образом, факультеты учащихся ничего не получат.

Эндрю Уорвик обратил внимание на исторический вопрос учений:

Включение иллюстративных упражнений и задач в конце глав в учебники математической физики сейчас настолько распространено, что кажется обычным явлением, но важно понимать, что этот педагогический прием возник сравнительно недавно и был введен в конкретном историческом контексте.

В отчете об экзаменах по математике , проводимых в Кембриджском университете , он отмечает:

Такое кумулятивное, конкурентное обучение также было более эффективно достигнуто частными репетиторами, использующими индивидуальное обучение, специально подготовленные рукописи и оцененные примеры и задачи, чем преподаватели колледжей, ведущие большие классы в посредственном темпе.

Объясняя связь осмотра и упражнения, он пишет

... к 1830-м годам именно задачи на экзаменационных работах, а не упражнения в учебниках, определяли стандарт, к которому стремились амбициозные студенты ... [студенты Кембриджа] не только ожидали, что найдут путь через простой набросок примера , но их учили рассматривать такие упражнения как полезную подготовку к решению сложных задач на экзаменах.

Объясняя, как укоренилась реформа, Уорвик писал:

В Кембридже было широко распространено мнение, что лучший способ преподавания математики, включая новые аналитические методы, — это практические примеры и задачи, и к середине 1830-х годов некоторые из первого поколения молодых студентов колледжей обучались высшему анализу. Таким образом, они начали проводить собственные исследования и назначаться экспертами Tripos.

Уорвик сообщает, что в Германии Франц Эрнст Нойман примерно в то же время «разработал общую систему поэтапных упражнений, которая знакомила учащихся с иерархией основных математических навыков и методов, и... начал конструировать свои собственные наборы задач , с помощью которых его ученики могли научитесь своему ремеслу». В России Стефан Тимошенко реформировал обучение упражнениям. В 1913 преподавал сопротивление материалов в Петербургском государственном университете путей сообщения . Как он писал в 1968 году,

[Практических] занятий в институте не проводилось, а на экзаменах студентам задавались только теоретические вопросы из принятого учебника. Мне пришлось как можно скорее положить конец такому обучению. Студенты ясно понимали ситуацию, осознавали необходимость лучшего усвоения предмета и не возражали против резкого увеличения нагрузки. Основная трудность была с преподавателями, точнее, с экзаменаторами, которые привыкли сдавать экзамены по книге. Постановка практических задач на экзаменах усложняла им работу. Это были люди преклонного возраста... единственной надеждой было привлечь к преподаванию более молодых людей.

См. также

• Алгоритм
• Эффект отработанного примера

Внешние ссылки

• Татьяна Афанасьева (1931) Упражнения по экспериментальной геометрии из Тихоокеанского института математических наук .
• Владимир Арнольд (2004) Упражнения для школьников от 5 до 15 лет на платформе IMAGINARY.
• Джеймс Альфред Юинг (1911) Примеры по математике, механике, навигации и морской астрономии, теплу и пару, электричеству, для использования младшими офицерами на плаву из Интернет-архива .
• Джим Хефферон и другие (2004) Линейная алгебра в Wikibooks