Соединение Эресманн

В дифференциальной геометрии связность Эресмана (в честь французского математика Шарля Эресмана , который первым формализовал это понятие) — это версия понятия связности , которая имеет смысл на любом гладком расслоении . В частности, он не опирается на возможную структуру векторного расслоения базового расслоения, но, тем не менее, линейные соединения можно рассматривать как особый случай. Другим важным частным случаем связностей Эресмана являются главные связности на главных расслоениях , которые должны быть эквивариантны в действии главной группы Ли .

Введение

Ковариантная производная в дифференциальной геометрии — это линейный дифференциальный оператор принимает производную по направлению сечения векторного расслоения образом , который ковариантным . Это также позволяет сформулировать понятие о параллельном участке жгута в направлении вектора: участок s параллелен вдоль вектора $X$ если $\nabla _{X}s=0$. Таким образом, ковариантная производная обеспечивает как минимум две вещи: дифференциальный оператор и представление о том, что значит быть параллельным в каждом направлении. Соединение Эресмана полностью исключает дифференциальный оператор и аксиоматически определяет соединение в терминах секций, параллельных в каждом направлении ( Эресманн 1950 ). В частности, связность Эресмана выделяет векторное подпространство каждого касательного пространства к общему пространству расслоения, называемому горизонтальным пространством . Раздел $s$ тогда горизонтально (т. е. параллельно) в направлении $X$ если ${\rm {d}}s(X)$ лежит в горизонтальном пространстве. Здесь мы касаемся $s$ как функция $s\colon M\to E$ с базы $M$ к пучку волокон $E$, так что ${\rm {d}}s\colon TM\to TE$ тогда это движение вперед касательных векторов. Горизонтальные пространства вместе образуют векторное подрасслоение $TE$.

Это имеет то преимущество, что его можно определить для гораздо более широкого класса структур, чем простые векторные расслоения. В частности, оно корректно определено на общем расслоении . Более того, многие особенности ковариантной производной все еще сохраняются: параллельный транспорт, кривизна и голономия .

Недостающим компонентом связи, помимо линейности, является ковариация . В случае классических ковариантных производных ковариация является апостериорным признаком производной. При их построении задается закон преобразования символов Кристоффеля , который не является ковариантным, и общая ковариантность производной в результате этого следует . Для связности Эресмана можно с самого начала наложить обобщенный ковариационный принцип, введя группу Ли, действующую на слоях расслоения. Соответствующим условием является требование, чтобы горизонтальные пространства были в определенном смысле эквивариантны относительно действия группы.

Последним штрихом к связности Эресмана является то, что ее можно представить в виде дифференциальной формы , почти так же, как и в случае связной формы . Если группа действует на слоях и связность эквивариантна, то и форма будет эквивариантной. определить кривизну как форму кривизны Кроме того, форма соединения позволяет также .

Формальное определение

Связность Эресмана — это выбор горизонтального подпространства. $H_{p}\subset T_{p}P$ для каждого $p\in P$, где $P$ — некоторое расслоение, обычно главное расслоение .

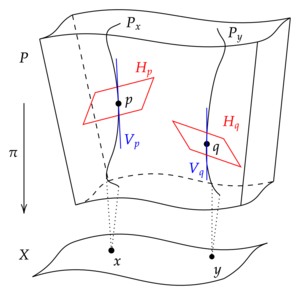
Позволять $\pi \colon E\to M$ быть гладким пучком волокон . Позволять

$V=\ker(\operatorname {d} \pi \colon TE\to TM)$

— вертикальный расслоение , состоящее из векторов, «касательных к слоям» E , т. е. слой V в точке $e\in E$ является $V_{e}=T_{e}(E_{\pi (e)})$. Этот подпакет $TE$ канонически определено, даже если не существует канонического подпространства, касающегося базового пространства M . (Конечно, эта асимметрия исходит из самого определения пучка волокон, который «имеет только одну проекцию». $\pi \colon E\to M$ в то время как продукт $E=M\times F$ было бы два.)

Определение через горизонтальные подпространства

Соединение Эресмана на $E$ представляет собой гладкое подрасслоение $H$ из $TE$, называемый горизонтальным расслоением связности, который дополнителен к V в том смысле, что он определяет в прямую сумму разложение $TE=H\oplus V$. Более подробно, горизонтальный пучок обладает следующими свойствами.

• Для каждой точки $e\in E$, $H_{e}$ является векторным подпространством касательного пространства $T_{e}E$ к $E$ в $e$, называемое горизонтальным подпространством соединения в $e$.
• $H_{e}$ зависит плавно от $e$.
• Для каждого $e\in E$, $H_{e}\cap V_{e}=\{0\}$.
• Любой касательный вектор в $T_{e}E$ (для любого $e\in E$) представляет собой сумму горизонтальной и вертикальной составляющей, так что $T_{e}E=H_{e}+V_{e}$.

Говоря более сложным языком, такое распределение горизонтальных пространств, удовлетворяющих этим свойствам, соответствует в точности гладкому сечению струйного расслоения J ¹ Э → Э.

Определение через форму подключения

Эквивалентно, пусть Φ — проекция на вертикальное расслоение V вдоль H (так что H = ker Φ ). Это определяется указанным выше в прямую сумму разложением ТЕ на горизонтальную и вертикальную части и иногда называется формой связи связи Эресмана. Таким образом, Φ — гомоморфизм векторного расслоения из TE в себя со следующими свойствами (проекций вообще):

• Ф ² = Ф ;
• Φ — тождество на V =Im Φ .

Обратно, если Φ — эндоморфизм векторного расслоения TE , удовлетворяющий этим двум свойствам, то H = ker Φ — горизонтальное подрасслоение связности Эресмана.

Наконец, заметим, что Φ линейным отображением каждого касательного пространства в себя, также можно рассматривать как TE -значную 1-форму на E. , будучи Это будет полезной точкой зрения в следующих разделах.

Параллельная транспортировка с помощью горизонтальных подъемников

Связность Эресмана также предписывает способ подъема кривых из базового многообразия M в полное пространство расслоения E так, чтобы касательные к кривой были горизонтальными. Эти горизонтальные лифты являются прямым аналогом параллельного транспорта для других вариантов формализма связи.

В частности, предположим, что γ ( t ) — гладкая кривая в M, проходящая через точку x = γ (0). Пусть e ∈ Ex _— точка слоя над x . Подъем — γ e через это кривая ${\tilde {\gamma }}(t)$ в полном пространстве E такая, что

${\tilde {\gamma }}(0)=e$, и $\pi ({\tilde {\gamma }}(t))=\gamma (t).$

Лифт является горизонтальным , если, кроме того, каждая касательная кривой лежит в горизонтальном подрасслоении TE :

${\tilde {\gamma }}'(t)\in H_{{\tilde {\gamma }}(t)}.$

можно показать С помощью теоремы о ранге-нулевости, примененной к π и Φ, , что каждый вектор X ∈ T _x M имеет уникальный горизонтальный подъем до вектора ${\tilde {X}}\in T_{e}E$. касательное поле к γ порождает горизонтальное векторное поле в полном пространстве расслоения обратного образа γ * E. В частности , По теореме Пикара–Линделёфа это векторное поле интегрируемо . Таким образом, для любой кривой и точки e над x = γ (0) существует единственный горизонтальный подъем γ γ через e за малое время t .

Обратите внимание, что для общих связей Эресмана горизонтальный подъем зависит от пути. Когда две гладкие кривые в M , совпадающие в точке γ ₁ (0) = γ ₂ (0) = x ₀ и пересекающиеся также в другой точке x ₁ ∈ M , поднимаются горизонтально к E через ту же самую e ∈ π ⁻¹ ( x ₀ ), они обычно проходят через разные точки π ⁻¹ ( х ₁ ). Это имеет важные последствия для дифференциальной геометрии расслоений: пространство сечений H не является подалгеброй Ли пространства векторных полей на E , поскольку оно (вообще) не замкнуто относительно скобки Ли векторных полей . Неспособность закрытия под скобкой Ли измеряется кривизной .

Характеристики

Кривизна

Пусть Φ — связность Эресмана. Тогда кривизна Φ определяется выражением

$R={\tfrac {1}{2}}[\varPhi ,\varPhi ]$

-] обозначает скобку Фрелихера-Ниенхейса Φ где [- , ∈ Ω ¹ ( E , TE ) сам с собой. Таким образом, R ∈ Ω ² ( E , TE ) — это две формы на E со значениями в TE, определяемыми формулой

$R(X,Y)=\varPhi \left([(\mathrm {id} -\varPhi )X,(\mathrm {id} -\varPhi )Y]\right)$,

или, другими словами,

$R\left(X,Y\right)=\left[X_{H},Y_{H}\right]_{V}$,

где X = X _H + X _V обозначает разложение прямой суммы на компоненты H и V соответственно. Из этого последнего выражения для кривизны видно, что она тождественно обращается в нуль тогда и только тогда, когда горизонтальное подрасслоение интегрируемо по Фробениусу . кривизна является условием интегрируемости горизонтального подрасслоения для получения поперечных сечений расслоения E → M. Таким образом ,

Кривизна связи Эресмана также удовлетворяет версии тождества Бьянки :

$\left[\varPhi ,R\right]=0$

где снова [-,-] — скобка Фрелихера-Нийенхейса Φ ∈ Ω ¹ ( E , TE ) и R ∈ Ω ² ( Э , ТЕМ ).

Полнота

иметь уникальные горизонтальные подъемы Связность Эресмана позволяет кривым локально . Для полной связности Эресмана кривую можно поднять горизонтально на всей ее области.

Голономия

Плоскостность связности локально соответствует интегрируемости по Фробениусу горизонтальных пространств. С другой стороны, неисчезающая кривизна предполагает наличие голономности связи.

Особые случаи

Главные расслоения и главные связи

Основная статья: Подключение (основной пакет)

Форма подключения основного пакета $\omega$ можно рассматривать как оператор проектирования на касательном расслоении $TP$ основного пакета $P$. Ядро формы связности задается горизонтальными подпространствами для соответствующей связности Эресмана.

Предположим, что — гладкое главное G -расслоение над M. E Тогда связность Эресмана H на E называется главной (Эресмановой) связностью. если он инвариантен относительно действия G на E в том смысле, что

$H_{eg}=\mathrm {d} (R_{g})_{e}(H_{e})$ для любых e ∈ E и g ∈ G ; здесь $\mathrm {d} (R_{g})_{e}$ обозначает дифференциал правого действия g E на точке в e .

Однопараметрические подгруппы группы G действуют вертикально на E . Дифференциал этого действия позволяет идентифицировать подпространство $V_{e}$ с алгеброй Ли g группы G , скажем, отображением $\iota \colon V_{e}\to {\mathfrak {g}}$. Тогда форму связности Φ связности Эресмана можно рассматривать как 1-форму ω на E со значениями в g , определяемыми формулой ω ( X ) = ι ( Φ ( X )).

Переосмысленная таким образом форма связи ω удовлетворяет следующим двум свойствам:

• Он преобразуется эквивариантно под действием G : $R_{h}^{*}\omega ={\hbox{Ad}}(h^{-1})\omega$ для всех h ∈ G , где R _h ^* — обратный образ при правом действии, а Ad — присоединенное представление группы G на ее алгебре Ли.
• Он отображает вертикальные векторные поля в связанные с ними элементы алгебры Ли: ω ( X ) = ι ( X ) для всех X ∈ V .

И наоборот, можно показать, что такая g -значная 1-форма на главном расслоении порождает горизонтальное распределение, удовлетворяющее вышеупомянутым свойствам.

Учитывая локальную тривиализацию, можно свести ω к горизонтальным векторным полям (в этой тривиализации). Он определяет 1-форму ω' на M посредством обратного образа . Форма со' полностью определяет со , но это зависит от выбора тривиализации. (Эту форму часто еще называют формой связности и обозначают просто ω .)

Векторные расслоения и ковариантные производные

Основная статья: Соединение (векторный пакет)

Предположим, что — гладкое векторное расслоение над M. E Тогда связность Эресмана H на E называется линейной (Эресмановой) связностью, He линейно _если зависит от e ∈ E _x для каждого x ∈ M . Чтобы уточнить это, пусть S _λ обозначает скалярное умножение на λ на E . Тогда H линейна тогда и только тогда, когда $H_{\lambda e}=\mathrm {d} (S_{\lambda })_{e}(H_{e})$для любого e ∈ E и скаляра λ.

Поскольку E — векторное расслоение, его вертикальное V изоморфно π * E. расслоение Следовательно, если s — сечение E , то Φ (d s ): TM → s * V знак равно s * π * E знак равно E . Это морфизм векторного расслоения и, следовательно, задается секцией ∇ s векторного расслоения Hom( TM , E ). Тот факт, что связность Эресмана является линейной, означает, что она, кроме того, проверяется для каждой функции $f$ на $M$ правило Лейбница, т.е. $\nabla (fs)=f\nabla (s)+d(f)\otimes s$ , следовательно, является ковариантной производной s , и .

И наоборот, ковариантная производная ∇ на векторном расслоении определяет линейную связность Эресмана, определяя H _e , для e ∈ E с x = π ( e ), как образ d s _x ( T _x M ), где s — сечение E с s ( x ) = e и ∇ _X s знак равно 0 для всех X ∈ T _x M .

Обратите внимание, что (по историческим причинам) термин «линейный» , когда он применяется к соединениям, иногда используется (например, слово «аффинное» — см. «Аффинное соединение ») для обозначения соединений, определенных на касательном расслоении или связке фреймов .

Связанные пакеты

Связность Эресмана на расслоении (наделенном структурной группой) иногда приводит к связности Эресмана на ассоциированном расслоении . Например, (линейное) соединение в векторном расслоении E как указано выше, обеспечивает параллелизм E , индуцирует соединение в соответствующем пучке кадров PE из E. , которое , И наоборот, связность в PE порождает (линейную) связность в E при условии, что связность в PE эквивариантна относительно действия полной линейной группы на шкалах (и, следовательно, является основной связностью ). Связность Эресмана не всегда может естественным образом индуцировать связность на ассоциированном расслоении. Например, неэквивариантная связность Эресмана на связке шкал векторного расслоения может не индуцировать связность на векторном расслоении.

Предположим, что — ассоциированный расслоение P , так что E = P × _GF E . G → -связность на E это связность Эресмана такая, что параллельное транспортное отображение τ : F _x — F _{x ′} задается G -преобразованием слоев (над достаточно близкими точками x и x ′ в M, соединенными кривой) .

Учитывая главное соединение на P , можно получить G соответствующем расслоении E = P × _GF -связность на посредством обратного образа .

И наоборот, по G -связности на E можно восстановить основную связность на соответствующем главном расслоении P . Чтобы восстановить эту принципиальную связь, вводится понятие фрейма на типичном F. слое Поскольку G — конечномерная Группа Ли, эффективно действующая на F существовать конечная конфигурация точек ( y1 ₁ ,..., ym _{, должна} ) внутри F такая, что G -орбита R = {( gy _, ..., gy _m ) | g ∈ G } — главное однородное пространство G. группы Можно думать, что дает обобщение понятия рамки для G -действия на F. R Обратите внимание, что, поскольку R является главным однородным пространством для G , расслоение E ( R ассоциированное с E с типичным слоем R, является (эквивалентным) главному расслоению, ассоциированному с E. ) , Но оно также является подрасслоением m -кратного произведения E с самим собой. Распределение горизонтальных пространств на E вызывает распределение пространств в этом наборе продуктов. Поскольку параллельные транспортные карты, связанные с соединением, являются G -отображениями, они сохраняют подпространство E ( R ), и поэтому G -соединение спускается к главному G -соединению на E ( R ).

Таким образом, существует взаимно однозначное соответствие (с точностью до эквивалентности) между спусками главных связностей на ассоциированные расслоения и G -связности на ассоциированных расслоениях. По этой причине в категории расслоений со структурной группой G главное соединение содержит всю необходимую информацию для G -связностей на ассоциированных расслоениях. Следовательно, если нет веской причины рассматривать соединения в ассоциированных связках (как, например, в случае соединений Картана ), обычно работают непосредственно с основным соединением.

Ссылки

• Эресманн, Чарльз (1950), Бесконечно малые связи в дифференцируемом расслоенном пространстве (PDF) , Коллоквиум по топологии, Брюссель, Жорж Тон, Льеж; Masson & cie, Париж, стр. 29–55
• Эресманн, Чарльз (1952), Бесконечно малые связи в дифференцируемом расслоенном пространстве (PDF) , Семинар Н. Бурбаки, том. 24, с. 153–168
• Элиасон, Х. (1967), «Геометрия многообразий отображений», Журнал дифференциальной геометрии , 1 : 169–194.
• Кобаяши, Шошичи (1957), «Теория связей» , Анн. Мат. Приложение Пура. , 43 : 119–194, doi : 10.1007/BF02411907 , MR   0096276 , S2CID   120972987
• Кобаяши, Сошичи ; Номидзу, Кацуми (1996a), Основы дифференциальной геометрии , том. 1 (Новое издание), Wiley-Interscience, ISBN  0-471-15733-3
• Кобаяши, Сошичи ; Номидзу, Кацуми (1996b), Основы дифференциальной геометрии , том. 2 (Новое издание), Wiley-Interscience, ISBN  978-0-471-15732-8
• Коларж, Иван; Михор, Питер; Словак, Январь (1993), Естественные операторы в дифференциальной геометрии (PDF) , Springer-Verlag, заархивировано из оригинала (PDF) 30 марта 2017 г. , получено 25 апреля 2007 г.
• Ланг, Серж (1999), Основы дифференциальной геометрии , Springer-Verlag, ISBN  0-387-98593-Х
• Лумисте, Юло (2001a) [1994], «Соединение на пучке волокон» , Энциклопедия математики , EMS Press
• Лумисте, Юло (2001b) [1994], «Соединения на многообразии» , Энциклопедия математики , EMS Press
• Риб, Жорж (1952), О некоторых топологических свойствах слоеных разновидностей , Париж: Герман

Дальнейшее чтение

• Рауль Ботт (1970) «Топологическое препятствие интегрируемости», Proc. Симп. Чистая математика. , 16 амер. Математика. Soc., Провиденс, Род-Айленд.
• Кубарский, Ян; Прадин, Жан; Рыбицкий, Томаш; Волак, Роберт, ред. (2007). Геометрия и топология многообразий: Математическое наследие Чарльза Эресмана к столетнему юбилею со дня его рождения . Публикации Банахового центра. Том. 76. Варшава: Польская академия наук . МР   2284825 .