спираль Эйлера

Двуконечная спираль Эйлера. Кривая продолжает сходиться к отмеченным точкам, поскольку t стремится к положительной или отрицательной бесконечности.

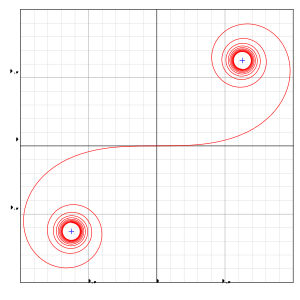
Спираль Эйлера — это кривая, кривизна которой изменяется линейно с длиной кривой (кривизна круговой кривой равна обратной величине радиуса). Эту кривую также называют клотоидой или спиралью Корню . Поведение интегралов Френеля можно проиллюстрировать с помощью спирали Эйлера — связи, впервые установленной Альфредом Мари Корню в 1874 году. Спираль Эйлера — это разновидность суперспирали , обладающая свойством монотонной функции кривизны.

Спираль Эйлера находит применение в расчетах дифракции . Они также широко используются в железнодорожном и автомобильном строительстве для проектирования переходных кривых между прямыми и криволинейными участками железных и автомобильных дорог. Аналогичное применение можно найти и в фотонных интегральных схемах . Принцип линейного изменения кривизны переходной кривой между касательной и круговой кривой определяет геометрию спирали Эйлера:

• Его кривизна начинается с нуля на прямом участке (касательной) и линейно увеличивается с длиной кривой.
• Там, где спираль Эйлера встречается с круговой кривой, ее кривизна становится равной кривизне последней.

История

Спираль имеет несколько названий, отражающих ее открытие и применение в различных областях. Тремя основными областями были упругие пружины («спираль Эйлера», 1744 г.), графические вычисления в дифракции света («спираль Корню», 1874 г.) и железнодорожные переходы («спираль железнодорожного перехода», 1890 г.).

Работа Леонарда Эйлера о спирали появилась после того, как Джеймс Бернулли поставил задачу в теории упругости: какой формы должна быть предварительно изогнутая проволочная пружина, чтобы при сплющивании путем нажатия на свободный конец она становилась прямой линией? Эйлер установил свойства спирали в 1744 году, отметив тогда, что кривая должна иметь два предела, точки, которые кривая огибает и вокруг, но никогда не достигает. Тридцать восемь лет спустя, в 1781 году, он сообщил о своем открытии формулы предела («по счастливой случайности»).

Огюстен Френель , работая в 1818 году над дифракцией света, разработал интеграл Френеля , определяющий ту же спираль. Он не знал ни об интегралах Эйлера, ни о связи их с теорией упругости. В 1874 году Альфред Мари Корню показал, что интенсивность дифракции можно определить по графику спирали, возведя в квадрат расстояние между двумя точками на графике. В своем биографическом очерке Корню Анри Пуанкаре высоко оценил преимущества «спирали Корню» перед «неприятным множеством волосатых интегральных формул». Эрнесто Чезаро решил назвать ту же кривую «клотоидой» в честь Клото , одной из трёх Судьб, прядущих нить жизни в греческой мифологии.

Третье независимое открытие произошло в 1800-х годах, когда различные инженеры железнодорожного транспорта искали формулу постепенного искривления формы пути. К 1880 году Артур Ньюэлл Тэлбот разработал интегральные формулы и их решение, которые он назвал «спиралью железнодорожного перехода». Связь с работой Эйлера не была установлена ​​до 1922 года.

Приложения

Отслеживать кривую перехода

Основная статья: Кривая перехода трека

Анимация, изображающая эволюцию спирали Корню с касательной окружностью с тем же радиусом кривизны, что и на ее кончике, также известной как соприкасающаяся окружность .

Чтобы двигаться по круговой траектории, объект должен подвергаться центростремительному ускорению (например: Луна вращается вокруг Земли под действием силы тяжести; автомобиль поворачивает передние колеса внутрь, чтобы создать центростремительную силу). Если бы транспортное средство, движущееся по прямому пути, внезапно перешло на тангенциальный круговой путь, ему потребовалось бы внезапное переключение центростремительного ускорения в точке касания с нуля на требуемое значение; этого было бы трудно достичь (представьте себе, что водитель мгновенно перемещает рулевое колесо с прямой линии в положение поворота, и автомобиль фактически делает это), оказывая механическое напряжение на части автомобиля и вызывая большой дискомфорт (из-за бокового рывка ).

На первых железных дорогах такое мгновенное приложение боковой силы не было проблемой, поскольку использовались низкие скорости и повороты с широким радиусом (боковые силы, действующие на пассажиров, и боковое раскачивание были небольшими и терпимыми). Поскольку скорости железнодорожного транспорта с годами увеличивались, стало очевидно, что необходим сервитут, чтобы центростремительное ускорение плавно увеличивалось с пройденным расстоянием. Учитывая выражение центростремительного ускорения ⁠ v ² / r ⁠ , очевидным решением является создание кривой сервитута, кривизна которой ⁠ 1 / R ⁠ , увеличивается линейно с увеличением пройденного расстояния. Эта геометрия представляет собой «клотоид», другое название спирали Эйлера.

Не зная о решении Леонарда Эйлера по геометрии , Рэнкин сослался на кубическую кривую (полиномиальную кривую степени 3), которая является приближением спирали Эйлера для малых угловых изменений точно так же, как парабола является приближением круговой кривой. изгиб.

Мари Альфред Корню (а позже и некоторые инженеры-строители) также самостоятельно решили расчет спирали Эйлера. Спирали Эйлера в настоящее время широко используются в железнодорожном и автомобильном строительстве для обеспечения перехода или облегчения между касательной и горизонтальной круговой кривой.

Оптика

В оптике используется термин «спираль Корню». Спираль Корню можно использовать для описания дифракционной картины. Рассмотрим плоскую волну с векторной амплитудой E ₀ e ^{− джкз} который дифрагируется на «ножевом крае» высотой h выше x = 0 на плоскости z = 0 . Тогда поле дифрагированной волны можно выразить как $$\mathbf {E} (x,z)=E_{0}e^{-jkz}{\frac {\mathrm {Fr} (\infty )-\mathrm {Fr} \left({\sqrt {\frac {2}{\lambda z}}}(h-x)\right)}{\mathrm {Fr} (\infty )-\mathrm {Fr} (-\infty )}},$$где Fr( x ) — интегральная функция Френеля, образующая спираль Корню на комплексной плоскости.

Итак, чтобы упростить расчет затухания плоской волны при ее дифракции от острия ножа, можно использовать диаграмму спирали Корню, представляя величины Fr( a ) − Fr( b ) как физические расстояния между представленными точками на Fr( a ) и Fr( b ) для соответствующих a и b . Это облегчает грубый расчет затухания плоской волны ножевой кромкой высоты h в месте ( x , z ) за ножевой кромкой.

Интегрированная оптика

Изгибы с плавно меняющимся радиусом кривизны по спирали Эйлера также используются для уменьшения потерь в фотонных интегральных схемах , либо в одномодовых волноводах, либо в одномодовых волноводах . для сглаживания резкого изменения кривизны и подавления связи с модами излучения или в многомодовых волноводах, для подавления связи с модами более высокого порядка и обеспечения эффективной одномодовой работы.Новаторское и очень элегантное применение спирали Эйлера в волноводах было сделано еще в 1957 году. с полым металлическим волноводом для микроволн. Идея заключалась в том, чтобы использовать тот факт, что прямой металлический волновод можно физически согнуть, чтобы естественным образом принять форму постепенного изгиба, напоминающую спираль Эйлера.

Интеграл по траектории Фейнмана

В формулировке квантовой механики с интегралом по путям амплитуду вероятности распространения между двумя точками можно визуализировать, соединив стрелки фазы действия для каждого временного шага между двумя точками. Стрелки закручиваются вокруг каждой конечной точки, образуя так называемую спираль Корню.

Автогонки

Автор автоспорта Адам Бруйяр продемонстрировал использование спирали Эйлера для оптимизации гоночной траектории во время входа в поворот.

Типография и цифровая векторная графика

Раф Левиен выпустил Spiro как набор инструментов для дизайна кривых, особенно дизайна шрифтов, в 2007 году. по свободной лицензии. Этот набор инструментов был довольно быстро впоследствии реализован в инструменте дизайна шрифтов Fontforge и цифровом векторном рисовании Inkscape .

Картографическая проекция

Разрезание сферы по спирали шириной ⁠ 1 / N ⁠ и сглаживание полученной формы дает спираль Эйлера, когда n стремится к бесконечности. Если сферой является глобус , это создает картографическую проекцию , искажение которой стремится к нулю, поскольку n стремится к бесконечности.

Формы усов

Естественная форма усов крыс хорошо аппроксимируется сегментами спиралей Эйлера; у одной крысы все усы можно аппроксимировать как сегменты одной спирали. Два параметра уравнения Чезаро для сегмента спирали Эйлера могут дать представление о механизме кератинизации роста усов.

Формулировка

Символы

Р	Радиус кривизны
Р с	Радиус круговой кривой на конце спирали
я	Угол кривой от начала спирали (бесконечный R ) до определенной точки спирали. Его также можно измерить как угол между начальной касательной и касательной в рассматриваемой точке.
θ с	Угол полной спиральной кривой
Л , с	Длина измерена вдоль спиральной кривой от ее исходного положения.
Л с , так о	Длина спиральной кривой

showВывод

The graph on the right illustrates an Euler spiral used as an easement (transition) curve between two given curves, in this case a straight line (the negative x axis) and a circle. The spiral starts at the origin in the positive x direction and gradually turns anticlockwise to osculate the circle. The spiral is a small segment of the above double-end Euler spiral in the first quadrant. From the definition of the curvature, $${\frac {1}{R}}={\frac {d\theta }{ds}}\propto s$$ i.e., $${\begin{aligned}Rs={\text{constant}}&=R_{c}s_{o}\\{\frac {d\theta }{ds}}&={\frac {s}{R_{c}s_{o}}}\end{aligned}}$$We write in the format, $${\frac {d\theta }{ds}}=2a^{2}s$$ where $$2a^{2}={\frac {1}{R_{c}s_{o}}}$$ or $$a={\frac {1}{\sqrt {2R_{c}s_{o}}}}$$thus $$\theta =(as)^{2}$$Now $$x=\int _{0}^{L}\cos \theta \,ds=\int _{0}^{L}\cos \left[\left(as\right)^{2}\right]\,ds$$If $$s'=as$$Then $$ds={\frac {ds'}{a}}$$Thus $${\begin{aligned}x&={\frac {1}{a}}\int _{0}^{L'}\cos \left(s^{2}\right)\,ds\\y&=\int _{0}^{L}\sin \theta \,ds\\&=\int _{0}^{L}\sin \left[\left(as\right)^{2}\right]\,ds\\&={\frac {1}{a}}\int _{0}^{L'}\sin \left({s}^{2}\right)\,ds\end{aligned}}$$

Разложение интеграла Френеля

Основная статья: интеграл Френеля

Если a = 1 , что имеет место для нормализованной кривой Эйлера, то декартовы координаты задаются интегралами Френеля (или интегралами Эйлера): $${\begin{aligned}C(L)&=\int _{0}^{L}\cos \left(s^{2}\right)\,ds\\S(L)&=\int _{0}^{L}\sin \left(s^{2}\right)\,ds\end{aligned}}$$

Нормализация

Для данной кривой Эйлера с: $$2RL=2R_{c}L_{s}={\frac {1}{a^{2}}}$$или $${\frac {1}{R}}={\frac {L}{R_{c}L_{s}}}=2a^{2}L$$затем $${\begin{aligned}x&={\frac {1}{a}}\int _{0}^{L'}\cos \left(s^{2}\right)\,ds\\y&={\frac {1}{a}}\int _{0}^{L'}\sin \left(s^{2}\right)\,ds\end{aligned}}$$где $${\begin{aligned}L'&=aL\\a&={\frac {1}{\sqrt {2R_{c}L_{s}}}}.\end{aligned}}$$

Таким образом, процесс получения решения ( x , y ) спирали Эйлера можно описать как:

• Отобразить L исходной спирали Эйлера путем умножения на коэффициент a на L ′ нормализованной спирали Эйлера;
• Найдите ( x ′, y ′) по интегралам Френеля; и
• Отобразите ( x ′, y ′) в ( x , y ) путем масштабирования (денормализации) с коэффициентом ⁠ 1 / а ⁠ . Обратите внимание, что ⁠ 1 / а ⁠ > 1 .

В процессе нормализации $${\begin{aligned}R'_{c}&={\frac {R_{c}}{\sqrt {2R_{c}L_{s}}}}={\sqrt {\frac {R_{c}}{2L_{s}}}}\\L'_{s}&={\frac {L_{s}}{\sqrt {2R_{c}L_{s}}}}={\sqrt {\frac {L_{s}}{2R_{c}}}}\end{aligned}}$$Затем $$2R'_{c}L'_{s}=2{\sqrt {\frac {R_{c}}{2L_{s}}}}{\sqrt {\frac {L_{s}}{2R_{c}}}}={\frac {2}{2}}=1$$

Обычно нормализация уменьшает L ′ до небольшого значения (менее 1) и приводит к хорошим сходящимся характеристикам интеграла Френеля, управляемым всего с несколькими членами (ценой повышенной числовой нестабильности расчета, особенно для больших значений θ ). .

Иллюстрация

Данный: $${\begin{aligned}R_{c}&=300\,\mathrm {m} \\L_{s}&=100\,\mathrm {m} \end{aligned}}$$Затем $$\theta _{s}={\frac {L_{s}}{2R_{c}}}={\frac {100}{2\times 300}}={\frac {1}{6}}\ \mathrm {radian}$$и $$2R_{c}L_{s}=60\,000$$

Мы уменьшаем спираль Эйлера на √ 60 000 , т.е. на 100 √ 6, до нормализованной спирали Эйлера, которая имеет: $${\begin{aligned}R'_{c}&={\tfrac {3}{\sqrt {6}}}\,\mathrm {m} \\L'_{s}&={\tfrac {1}{\sqrt {6}}}\,\mathrm {m} \\2R'_{c}L'_{s}&=2\times {\tfrac {3}{\sqrt {6}}}\times {\tfrac {1}{\sqrt {6}}}\\&=1\end{aligned}}$$и $$\theta _{s}={\frac {L'_{s}}{2R'_{c}}}={\frac {\frac {1}{\sqrt {6}}}{2\times {\frac {3}{\sqrt {6}}}}}={\frac {1}{6}}\ \mathrm {radian}$$

Два угла θs _{одинаковы} . Таким образом, это подтверждает, что исходная и нормированная спирали Эйлера геометрически подобны. Локус нормализованной кривой можно определить из интеграла Френеля, а локус исходной спирали Эйлера можно получить путем увеличения или денормализации.

Другие свойства нормализованных спиралей Эйлера

Нормализованные спирали Эйлера можно выразить как: $${\begin{aligned}x&=\int _{0}^{L}\cos \left(s^{2}\right)\,ds\\y&=\int _{0}^{L}\sin \left(s^{2}\right)\,ds\end{aligned}}$$или выразить в виде степенного ряда : $${\begin{aligned}x&=\left.\sum _{i=0}^{\infty }{\frac {(-1)^{i}}{(2i)!}}{\frac {s^{4i+1}}{4i+1}}\right|_{0}^{L}&&=\sum _{i=0}^{\infty }{\frac {(-1)^{i}}{(2i)!}}{\frac {L^{4i+1}}{4i+1}}\\y&=\left.\sum _{i=0}^{\infty }{\frac {(-1)^{i}}{(2i+1)!}}{\frac {s^{4i+3}}{4i+3}}\right|_{0}^{L}&&=\sum _{i=0}^{\infty }{\frac {(-1)^{i}}{(2i+1)!}}{\frac {L^{4i+3}}{4i+3}}\end{aligned}}$$

Нормализованная спираль Эйлера будет сходиться к одной точке в пределе, когда параметр L приближается к бесконечности, что можно выразить как: $${\begin{aligned}x^{\prime }&=\lim _{L\to \infty }\int _{0}^{L}\cos \left(s^{2}\right)\,ds&&={\frac {1}{2}}{\sqrt {\frac {\pi }{2}}}\approx 0.6267\\y^{\prime }&=\lim _{L\to \infty }\int _{0}^{L}\sin \left(s^{2}\right)\,ds&&={\frac {1}{2}}{\sqrt {\frac {\pi }{2}}}\approx 0.6267\end{aligned}}$$

Нормализованные спирали Эйлера обладают следующими свойствами: $${\begin{aligned}2R_{c}L_{s}&=1\\\theta _{s}&={\frac {L_{s}}{2R_{c}}}=L_{s}^{2}\end{aligned}}$$и $${\begin{aligned}\theta &=\theta _{s}\cdot {\frac {L^{2}}{L_{s}^{2}}}=L^{2}\\{\frac {1}{R}}&={\frac {d\theta }{dL}}=2L\end{aligned}}$$

Обратите внимание, что 2 R _c L _s = 1 также означает ⁠ 1 / R _c ⁠ = 2 L _s , что соответствует последнему математическому утверждению.

См. также

• Список спиралей

Дальнейшее чтение

• Келлог, Норман Бенджамин (1907). Кривая перехода или кривая адаптации (3-е изд.). Нью-Йорк: МакГроу.
• Р. Нейв, Спираль Корню , Гиперфизика (2002) (вместо t² используется πt²/2).
• Милтон Абрамовиц и Ирен А. Стегун, ред. Справочник по математическим функциям с формулами, графиками и математическими таблицами. Нью-Йорк: Дувр, 1972 г. (см. главу 7).
• «Формы петель американских горок» . Проверено 12 ноября 2010 г.

Внешние ссылки

• Вайсштейн, Эрик В. «Спираль Корню» . Математический мир .
• Спираль Эйлера в двумерных математических кривых
• Интерактивный пример с JSXGraph