Парамагнетизм

Парамагнетизм — это форма магнетизма , при которой некоторые материалы слабо притягиваются внешним магнитным полем и образуют внутренние индуцированные магнитные поля в направлении приложенного магнитного поля. В отличие от такого поведения, диамагнитные материалы отталкиваются магнитными полями и образуют индуцированные магнитные поля в направлении, противоположном направлению приложенного магнитного поля. ^{[ 1 ]} Парамагнитные материалы включают большинство химических элементов и некоторые соединения ; ^{[ 2 ]} они имеют относительную магнитную проницаемость немного больше 1 (т. е. небольшую положительную магнитную восприимчивость ) и, следовательно, притягиваются к магнитным полям. Магнитный момент, индуцированный приложенным полем, линеен по напряженности поля и достаточно слаб. Для обнаружения эффекта обычно требуются чувствительные аналитические весы, и современные измерения парамагнитных материалов часто проводятся с помощью СКВИДа магнитометра .

Paramagnetism is due to the presence of unpaired electrons in the material, so most atoms with incompletely filled atomic orbitals are paramagnetic, although exceptions such as copper exist. Due to their spin, unpaired electrons have a magnetic dipole moment and act like tiny magnets. An external magnetic field causes the electrons' spins to align parallel to the field, causing a net attraction. Paramagnetic materials include aluminium, oxygen, titanium, and iron oxide (FeO). Therefore, a simple rule of thumb is used in chemistry to determine whether a particle (atom, ion, or molecule) is paramagnetic or diamagnetic:^[3] если все электроны в частице спарены, то вещество, состоящее из этой частицы, диамагнитно; если у него есть неспаренные электроны, то вещество парамагнитно.

Unlike ferromagnets, paramagnets do not retain any magnetization in the absence of an externally applied magnetic field because thermal motion randomizes the spin orientations. (Some paramagnetic materials retain spin disorder even at absolute zero, meaning they are paramagnetic in the ground state, i.e. in the absence of thermal motion.) Thus the total magnetization drops to zero when the applied field is removed. Even in the presence of the field there is only a small induced magnetization because only a small fraction of the spins will be oriented by the field. This fraction is proportional to the field strength and this explains the linear dependency. The attraction experienced by ferromagnetic materials is non-linear and much stronger, so that it is easily observed, for instance, in the attraction between a refrigerator magnet and the iron of the refrigerator itself.

Relation to electron spins

Paramagnetism, ferromagnetism and spin waves

Constituent atoms or molecules of paramagnetic materials have permanent magnetic moments (dipoles), even in the absence of an applied field. The permanent moment generally is due to the spin of unpaired electrons in atomic or molecular electron orbitals (see Magnetic moment). In pure paramagnetism, the dipoles do not interact with one another and are randomly oriented in the absence of an external field due to thermal agitation, resulting in zero net magnetic moment. When a magnetic field is applied, the dipoles will tend to align with the applied field, resulting in a net magnetic moment in the direction of the applied field. In the classical description, this alignment can be understood to occur due to a torque being provided on the magnetic moments by an applied field, which tries to align the dipoles parallel to the applied field. However, the true origins of the alignment can only be understood via the quantum-mechanical properties of spin and angular momentum.

If there is sufficient energy exchange between neighbouring dipoles, they will interact, and may spontaneously align or anti-align and form magnetic domains, resulting in ferromagnetism (permanent magnets) or antiferromagnetism, respectively. Paramagnetic behavior can also be observed in ferromagnetic materials that are above their Curie temperature, and in antiferromagnets above their Néel temperature. At these temperatures, the available thermal energy simply overcomes the interaction energy between the spins.

In general, paramagnetic effects are quite small: the magnetic susceptibility is of the order of 10⁻³ to 10⁻⁵ for most paramagnets, but may be as high as 10⁻¹ for synthetic paramagnets such as ferrofluids.

Delocalization

Selected Pauli-paramagnetic metals^[4]
Material	Magnetic susceptibility, $\chi _{v}$ [10⁻⁵] (SI units)
Tungsten	6.8
Caesium	5.1
Aluminium	2.2
Lithium	1.4
Magnesium	1.2
Sodium	0.72

In conductive materials, the electrons are delocalized, that is, they travel through the solid more or less as free electrons. Conductivity can be understood in a band structure picture as arising from the incomplete filling of energy bands. In an ordinary nonmagnetic conductor the conduction band is identical for both spin-up and spin-down electrons. When a magnetic field is applied, the conduction band splits apart into a spin-up and a spin-down band due to the difference in magnetic potential energy for spin-up and spin-down electrons. Since the Fermi level must be identical for both bands, this means that there will be a small surplus of the type of spin in the band that moved downwards. This effect is a weak form of paramagnetism known as Pauli paramagnetism.

The effect always competes with a diamagnetic response of opposite sign due to all the core electrons of the atoms. Stronger forms of magnetism usually require localized rather than itinerant electrons. However, in some cases a band structure can result in which there are two delocalized sub-bands with states of opposite spins that have different energies. If one subband is preferentially filled over the other, one can have itinerant ferromagnetic order. This situation usually only occurs in relatively narrow (d-)bands, which are poorly delocalized.

s and p electrons

Generally, strong delocalization in a solid due to large overlap with neighboring wave functions means that there will be a large Fermi velocity; this means that the number of electrons in a band is less sensitive to shifts in that band's energy, implying a weak magnetism. This is why s- and p-type metals are typically either Pauli-paramagnetic or as in the case of gold even diamagnetic. In the latter case the diamagnetic contribution from the closed shell inner electrons simply wins over the weak paramagnetic term of the almost free electrons.

d and f electrons

Stronger magnetic effects are typically only observed when d or f electrons are involved. Particularly the latter are usually strongly localized. Moreover, the size of the magnetic moment on a lanthanide atom can be quite large as it can carry up to 7 unpaired electrons in the case of gadolinium(III) (hence its use in MRI). The high magnetic moments associated with lanthanides is one reason why superstrong magnets are typically based on elements like neodymium or samarium.

Molecular localization

The above picture is a generalization as it pertains to materials with an extended lattice rather than a molecular structure. Molecular structure can also lead to localization of electrons. Although there are usually energetic reasons why a molecular structure results such that it does not exhibit partly filled orbitals (i.e. unpaired spins), some non-closed shell moieties do occur in nature. Molecular oxygen is a good example. Even in the frozen solid it contains di-radical molecules resulting in paramagnetic behavior. The unpaired spins reside in orbitals derived from oxygen p wave functions, but the overlap is limited to the one neighbor in the O₂ molecules. The distances to other oxygen atoms in the lattice remain too large to lead to delocalization and the magnetic moments remain unpaired.

Theory

The Bohr–Van Leeuwen theorem proves that there cannot be any diamagnetism or paramagnetism in a purely classical system. The paramagnetic response has then two possible quantum origins, either coming from permanent magnetic moments of the ions or from the spatial motion of the conduction electrons inside the material. Both descriptions are given below.

Curie's law

For low levels of magnetization, the magnetization of paramagnets follows what is known as Curie's law, at least approximately. This law indicates that the susceptibility, $\chi$ , of paramagnetic materials is inversely proportional to their temperature, i.e. that materials become more magnetic at lower temperatures. The mathematical expression is: $\mathbf {M} =\chi \mathbf {H} ={\frac {C}{T}}\mathbf {H}$ where:

$\mathbf {M}$ is the resulting magnetization, measured in amperes/meter (A/m),
$\chi$ is the volume magnetic susceptibility (dimensionless),
$H$ is the auxiliary magnetic field (A/m),
$T$ is absolute temperature, measured in kelvins (K),
$C$ is a material-specific Curie constant (K).

Curie's law is valid under the commonly encountered conditions of low magnetization (μ_BH ≲ k_BT), but does not apply in the high-field/low-temperature regime where saturation of magnetization occurs (μ_BH ≳ k_BT) and magnetic dipoles are all aligned with the applied field. When the dipoles are aligned, increasing the external field will not increase the total magnetization since there can be no further alignment.

For a paramagnetic ion with noninteracting magnetic moments with angular momentum J, the Curie constant is related to the individual ions' magnetic moments, $C={\frac {n}{3k_{\mathrm {B} }}}\mu _{\mathrm {eff} }^{2}{\text{ where }}\mu _{\mathrm {eff} }=g_{J}\mu _{\mathrm {B} }{\sqrt {J(J+1)}}.$

where n is the number of atoms per unit volume. The parameter μ_eff is interpreted as the effective magnetic moment per paramagnetic ion. If one uses a classical treatment with molecular magnetic moments represented as discrete magnetic dipoles, μ, a Curie Law expression of the same form will emerge with μ appearing in place of μ_eff.

Derivation

Curie's Law can be derived by considering a substance with noninteracting magnetic moments with angular momentum J. If orbital contributions to the magnetic moment are negligible (a common case), then in what follows J = S. If we apply a magnetic field along what we choose to call the z-axis, the energy levels of each paramagnetic center will experience Zeeman splitting of its energy levels, each with a z-component labeled by M_J (or just M_S for the spin-only magnetic case). Applying semiclassical Boltzmann statistics, the magnetization of such a substance is $n{\bar {m}}={\frac {n\sum \limits _{M_{J}=-J}^{J}{\mu _{M_{J}}e^{{-E_{M_{J}}}/{k_{\mathrm {B} }T}\;}}}{\sum \limits _{M_{J}=-J}^{J}{e^{{-E_{M_{J}}}/{k_{\mathrm {B} }T}\;}}}}={\frac {n\sum \limits _{M_{J}=-J}^{J}{M_{J}g_{J}\mu _{\mathrm {B} }e^{{M_{J}g_{J}\mu _{\mathrm {B} }H}/{k_{\mathrm {B} }T}\;}}}{\sum \limits _{M_{J}=-J}^{J}{e^{{M_{J}g_{J}\mu _{\mathrm {B} }H}/{k_{\mathrm {B} }T}\;}}}}.$

Where $\mu _{M_{J}}$ is the z-component of the magnetic moment for each Zeeman level, so $\mu _{M_{J}}=M_{J}g_{J}\mu _{\mathrm {B} }-\mu _{\mathrm {B} }$ is called the Bohr magneton and g_J is the Landé g-factor, which reduces to the free-electron g-factor, g_S when J = S. (in this treatment, we assume that the x- and y-components of the magnetization, averaged over all molecules, cancel out because the field applied along the z-axis leave them randomly oriented.) The energy of each Zeeman level is $E_{M_{J}}=-M_{J}g_{J}\mu _{\mathrm {B} }H$ . For temperatures over a few K, $M_{J}g_{J}\mu _{\mathrm {B} }H/k_{\mathrm {B} }T\ll 1$ , and we can apply the approximation $e^{M_{J}g_{J}\mu _{\mathrm {B} }H/k_{\mathrm {B} }T\;}\simeq 1+M_{J}g_{J}\mu _{\mathrm {B} }H/k_{\mathrm {B} }T\;$ : ${\bar {m}}={\frac {\sum \limits _{M_{J}=-J}^{J}{M_{J}g_{J}\mu _{\mathrm {B} }e^{M_{J}g_{J}\mu _{\mathrm {B} }H/k_{\mathrm {B} }T\;}}}{\sum \limits _{M_{J}=-J}^{J}e^{M_{J}g_{J}\mu _{\mathrm {B} }H/k_{\mathrm {B} }T\;}}}\simeq g_{J}\mu _{\mathrm {B} }{\frac {\sum \limits _{M_{J}=-J}^{J}M_{J}\left(1+M_{J}g_{J}\mu _{\mathrm {B} }H/k_{\mathrm {B} }T\;\right)}{\sum \limits _{M_{J}=-J}^{J}\left(1+M_{J}g_{J}\mu _{\mathrm {B} }H/k_{\mathrm {B} }T\;\right)}}={\frac {g_{J}^{2}\mu _{\mathrm {B} }^{2}H}{k_{\mathrm {B} }T}}{\frac {\sum \limits _{-J}^{J}M_{J}^{2}}{\sum \limits _{M_{J}=-J}^{J}{(1)}}},$ which yields: ${\bar {m}}={\frac {g_{J}^{2}\mu _{\mathrm {B} }^{2}H}{3k_{\mathrm {B} }T}}J(J+1).$ The bulk magnetization is then $M=n{\bar {m}}={\frac {n}{3k_{\mathrm {B} }T}}\left[g_{J}^{2}J(J+1)\mu _{\mathrm {B} }^{2}\right]H,$ and the susceptibility is given by $\chi ={\frac {\partial M_{\rm {m}}}{\partial H}}={\frac {n}{3k_{\rm {B}}T}}\mu _{\mathrm {eff} }^{2}{\text{ ; and }}\mu _{\mathrm {eff} }=g_{J}{\sqrt {J(J+1)}}\mu _{\mathrm {B} }.$

When orbital angular momentum contributions to the magnetic moment are small, as occurs for most organic radicals or for octahedral transition metal complexes with d³ or high-spin d⁵ configurations, the effective magnetic moment takes the form ( with g-factor g_e = 2.0023... ≈ 2), $\mu _{\mathrm {eff} }\simeq 2{\sqrt {S(S+1)}}\mu _{\mathrm {B} }={\sqrt {N_{\rm {u}}(N_{\rm {u}}+2)}}\mu _{\mathrm {B} },$ where N_u is the number of unpaired electrons. In other transition metal complexes this yields a useful, if somewhat cruder, estimate.

When Curie constant is null, second order effects that couple the ground state with the excited states can also lead to a paramagnetic susceptibility independent of the temperature, known as Van Vleck susceptibility.

Pauli paramagnetism

For some alkali metals and noble metals, conduction electrons are weakly interacting and delocalized in space forming a Fermi gas. For these materials one contribution to the magnetic response comes from the interaction between the electron spins and the magnetic field known as Pauli paramagnetism. For a small magnetic field $\mathbf {H}$ , the additional energy per electron from the interaction between an electron spin and the magnetic field is given by:

\Delta E=-\mu _{0}\mathbf {H} \cdot {\boldsymbol {\mu }}_{e}=-\mu _{0}\mathbf {H} \cdot \left(-g_{e}{\frac {\mu _{\mathrm {B} }}{\hbar }}\mathbf {S} \right)=\pm \mu _{0}\mu _{\mathrm {B} }H,

where $\mu _{0}$ is the vacuum permeability, ${\boldsymbol {\mu }}_{e}$ is the electron magnetic moment, $\mu _{\rm {B}}$ is the Bohr magneton, $\hbar$ is the reduced Planck constant, and the g-factor cancels with the spin $\mathbf {S} =\pm \hbar /2$ . The $\pm$ indicates that the sign is positive (negative) when the electron spin component in the direction of $\mathbf {H}$ is parallel (antiparallel) to the magnetic field.

For low temperatures with respect to the Fermi temperature $T_{\rm {F}}$ (around 10⁴ kelvins for metals), the number density of electrons $n_{\uparrow }$ ( $n_{\downarrow }$ ) pointing parallel (antiparallel) to the magnetic field can be written as:

n_{\uparrow }\approx {\frac {n_{e}}{2}}-{\frac {\mu _{0}\mu _{\mathrm {B} }}{2}}g(E_{\mathrm {F} })H\quad ;\quad \left(n_{\downarrow }\approx {\frac {n_{e}}{2}}+{\frac {\mu _{0}\mu _{\mathrm {B} }}{2}}g(E_{\mathrm {F} })H\right),

with $n_{e}$ the total free-electrons density and $g(E_{\mathrm {F} })$ the electronic density of states (number of states per energy per volume) at the Fermi energy $E_{\mathrm {F} }$ .

In this approximation the magnetization is given as the magnetic moment of one electron times the difference in densities:

M=\mu _{\mathrm {B} }(n_{\downarrow }-n_{\uparrow })=\mu _{0}\mu _{\mathrm {B} }^{2}g(E_{\mathrm {F} })H,

which yields a positive paramagnetic susceptibility independent of temperature:

\chi _{\mathrm {P} }=\mu _{0}\mu _{\mathrm {B} }^{2}g(E_{\mathrm {F} }).

The Pauli paramagnetic susceptibility is a macroscopic effect and has to be contrasted with Landau diamagnetic susceptibility which is equal to minus one third of Pauli's and also comes from delocalized electrons. The Pauli susceptibility comes from the spin interaction with the magnetic field while the Landau susceptibility comes from the spatial motion of the electrons and it is independent of the spin. In doped semiconductors the ratio between Landau's and Pauli's susceptibilities changes as the effective mass of the charge carriers $m^{*}$ can differ from the electron mass $m_{e}$ .

The magnetic response calculated for a gas of electrons is not the full picture as the magnetic susceptibility coming from the ions has to be included. Additionally, these formulas may break down for confined systems that differ from the bulk, like quantum dots, or for high fields, as demonstrated in the De Haas-Van Alphen effect.

Pauli paramagnetism is named after the physicist Wolfgang Pauli. Before Pauli's theory, the lack of a strong Curie paramagnetism in metals was an open problem as the leading Drude model could not account for this contribution without the use of quantum statistics. Pauli paramagnetism and Landau diamagnetism are essentially applications of the spin and the free electron model, the first is due to intrinsic spin of electrons; the second is due to their orbital motion.^[5]^[6]

Examples of paramagnets

Materials that are called "paramagnets" are most often those that exhibit, at least over an appreciable temperature range, magnetic susceptibilities that adhere to the Curie or Curie–Weiss laws. In principle any system that contains atoms, ions, or molecules with unpaired spins can be called a paramagnet, but the interactions between them need to be carefully considered.

Systems with minimal interactions

Самым узким определением было бы следующее: система с непарными спинами, не взаимодействующими друг с другом. В этом самом узком смысле единственный чистый парамагнетик представляет собой разбавленный газ из одноатомных атомов водорода . Каждый атом имеет один невзаимодействующий неспаренный электрон.

Газ атомов лития уже имеет два спаренных остовных электрона, которые вызывают диамагнитный отклик противоположного знака. Строго говоря, Li представляет собой смешанную систему, хотя, по общему признанию, диамагнитная составляющая слаба и ею часто пренебрегают. В случае более тяжелых элементов диамагнитный вклад становится более важным, а в случае металлического золота он доминирует в свойствах. Элемент водород практически никогда не называют «парамагнитным», поскольку одноатомный газ стабилен только при чрезвычайно высокой температуре; Атомы H объединяются, образуя молекулярный H2 _, и при этом магнитные моменты теряются ( гасятся ) из-за пары спинов. Следовательно, водород диамагнитен , и то же самое справедливо и для многих других элементов. Хотя электронная конфигурация отдельных атомов (и ионов) большинства элементов содержит неспаренные спины, они не обязательно являются парамагнитными, поскольку при температуре окружающей среды тушение является скорее правилом, чем исключением. Тенденция к тушению наиболее слаба для f-электронов, поскольку f (особенно 4 f ) орбитали радиально сужены и лишь слабо перекрываются с орбиталями соседних атомов. Следовательно, элементы лантаноидов с неполностью заполненными 4f-орбиталями являются парамагнитными или магнитоупорядоченными. ^{[ 7 ]}

Значения μ _eff для типичных d ³ и д ⁵ комплексы переходных металлов. ^{[ 8 ]}
Материал	μ _эфф /μ _B
[Cr(NH ₃ ) ₆ ]Br ₃	3.77
К ₃ [Cr(CN) ₆ ]	3.87
К ₃ [МоСl ₆ ]	3.79
К ₄ [В(CN) ₆ ]	3.78
[Mn(NH ₃ ) ₆ ]Cl ₂	5.92
(NH ₄ ) ₂ [Mn(SO ₄ ) ₂ ]·6H ₂ O	5.92
NH ₄ [Fe(SO ₄ ) ₂ ]·12H ₂ O	5.89

Таким образом, парамагнетики с конденсированной фазой возможны только в том случае, если взаимодействия спинов, приводящие либо к тушению, либо к упорядочению, сдерживаются структурной изоляцией магнитных центров. Это справедливо для двух классов материалов:

Молекулярные материалы с (изолированным) парамагнитным центром.
- Хорошими примерами являются координационные комплексы d- или f-металлов или белков с такими центрами, например миоглобин . В таких материалах органическая часть молекулы действует как оболочка, защищающая спины от соседей.
- Маленькие молекулы могут быть стабильными в радикальной форме, кислород O ₂ хорошим примером является . Такие системы довольно редки, поскольку они имеют тенденцию быть довольно реактивными.
Разбавленные системы.
- Растворение парамагнитных частиц в диамагнитной решетке при малых концентрациях, например Nd. ³⁺ в CaCl ₂ будет разделять ионы неодима на достаточно большие расстояния, чтобы они не взаимодействовали. Такие системы имеют первостепенное значение для того, что можно считать наиболее чувствительным методом изучения парамагнитных систем: ЭПР .

Системы с взаимодействиями

Идеализированное поведение Кюри – Вейсса; NB T _C =θ, но T _N не является θ. Парамагнитные режимы обозначены сплошными линиями. Вблизи T _N или T _C поведение обычно отклоняется от идеального.

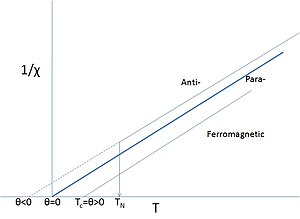
Как говорилось выше, многие материалы, содержащие d- или f-элементы, сохраняют негашеные спины. Соли таких элементов часто проявляют парамагнитное поведение, но при достаточно низких температурах магнитные моменты могут упорядочиваться. Такие материалы нередко называют «парамагнетиками», имея в виду их парамагнитное поведение выше точек Кюри или Нееля, особенно если такие температуры очень низкие или никогда не измерялись должным образом. Даже в отношении железа нередко можно сказать, что железо становится парамагнетиком выше своей относительно высокой точки Кюри. В этом случае точка Кюри рассматривается как фазовый переход между ферромагнетиком и «парамагнетиком». Слово «парамагнетик» теперь просто относится к линейному отклику системы на приложенное поле, температурная зависимость которого требует исправленной версии закона Кюри, известного как закон Кюри-Вейсса :

\mathbf {M} ={\frac {C}{T-\theta }}\mathbf {H}

Этот измененный закон включает член θ, который описывает обменное взаимодействие, которое присутствует, хотя и преодолевается тепловым движением. Знак θ зависит от того, преобладают ли ферро- или антиферромагнитные взаимодействия, и он редко бывает точно нулевым, за исключением упомянутых выше разбавленных изолированных случаев.

Очевидно, что парамагнитное описание Кюри–Вейсса выше T _N или T _C представляет собой несколько иную интерпретацию слова «парамагнетик», поскольку оно не подразумевает отсутствие взаимодействий, а, скорее, то, что магнитная структура является случайной в отсутствие внешнего поля. при этих достаточно высоких температурах. Даже если θ близко к нулю, это не означает отсутствия взаимодействий, а лишь то, что ориентирующие ферро- и антиориентирующие антиферромагнитные взаимодействия компенсируются. Дополнительная сложность заключается в том, что взаимодействия часто различны в разных направлениях кристаллической решетки ( анизотропия ), что приводит к сложным магнитным структурам , когда-то упорядоченным.

Случайность структуры также применима ко многим металлам, которые демонстрируют чистый парамагнитный отклик в широком диапазоне температур. Однако они не подчиняются закону типа Кюри в зависимости от температуры; часто они более или менее независимы от температуры. Этот тип поведения носит странствующий характер и лучше называется парамагнетизмом Паули, но нередко можно увидеть, например, металлический алюминий, называемый «парамагнетиком», даже несмотря на то, что взаимодействия достаточно сильны, чтобы придать этому элементу очень хорошую электропроводность. .

Суперпарамагнетики

Некоторые материалы демонстрируют индуцированное магнитное поведение, которое соответствует закону типа Кюри, но с исключительно большими значениями констант Кюри. Эти материалы известны как суперпарамагнетики . Для них характерен сильный ферромагнитный или ферримагнитный тип связи с доменами ограниченного размера, ведущими себя независимо друг от друга. По объемным свойствам такая система напоминает парамагнетик, но на микроскопическом уровне они упорядочены. Материалы действительно демонстрируют температуру упорядочения, выше которой поведение возвращается к обычному парамагнетизму (с взаимодействием). Хорошим примером являются феррожидкости , но это явление может происходить и внутри твердых тел, например, когда разбавленные парамагнитные центры вводятся в сильную коллективизированную среду ферромагнитной связи, например, когда Fe заменяется на TlCu ₂ Se ₂ или сплав AuFe. Такие системы содержат ферромагнитно связанные кластеры, которые вымерзают при более низких температурах. Их еще называют миктомагнетиками .

См. также

Магнитохимия

Ссылки

^ Мисслер, Г.Л. и Тарр, Д.А. (2010) Неорганическая химия , 3-е изд., Издательство Pearson/Prentice Hall, ISBN 0-13-035471-6 .
^ парамагнетизм . Британская энциклопедия
^ «Магнитные свойства» . Химия LibreTexts . 02.10.2013 . Проверено 21 января 2020 г.
^ Нейв, Карл Л. «Магнитные свойства твердых тел» . Гиперфизика . Проверено 9 ноября 2008 г.
^ Паули, Z.Phys. 41, 81, 1927 г.
^ Ландау, Z.Phys. 64, 629, 1930 г.
^ Дженсен, Дж. и Маккинтош, Арканзас (1991). Редкоземельный магнетизм . Оксфорд: Кларендон Пресс. Архивировано из оригинала 12 декабря 2010 г. Проверено 12 июля 2009 г.
^ Орчард, AF (2003) Магнитохимия . Издательство Оксфордского университета.

Дальнейшее чтение

Фейнмановские лекции по физике Vol. II, гл. 35: «Парамагнетизм и магнитный резонанс».
Чарльз Киттель, Введение в физику твердого тела (Wiley: Нью-Йорк, 1996).
Джон Дэвид Джексон, Классическая электродинамика (Wiley: Нью-Йорк, 1999).

Внешние ссылки

«Магнетизм: модели и механизмы» в книге Э. Паварини, Э. Коха и У. Шольвека: Эмерджентные явления в коррелированной материи , Юлих, 2013, ISBN 978-3-89336-884-6

[1] Мисслер, Г.Л. и Тарр, Д.А. (2010) Неорганическая химия , 3-е изд., Издательство Pearson/Prentice Hall, ISBN 0-13-035471-6 .

[brit-2] парамагнетизм . Британская энциклопедия

[3] «Магнитные свойства» . Химия LibreTexts . 02.10.2013 . Проверено 21 января 2020 г.

[magneticValues-4] Нейв, Карл Л. «Магнитные свойства твердых тел» . Гиперфизика . Проверено 9 ноября 2008 г.

[5] Паули, Z.Phys. 41, 81, 1927 г.

[6] Ландау, Z.Phys. 64, 629, 1930 г.

[7] Дженсен, Дж. и Маккинтош, Арканзас (1991). Редкоземельный магнетизм . Оксфорд: Кларендон Пресс. Архивировано из оригинала 12 декабря 2010 г. Проверено 12 июля 2009 г.

[8] Орчард, AF (2003) Магнитохимия . Издательство Оксфордского университета.

[ 1 ]

[ 2 ]

[3]

[4]

[5]

[6]

[ 7 ]

[ 8 ]

v т и Магнетизм
Magnetic response	diamagnetism superdiamagnetism paramagnetism superparamagnetism Van Vleck paramagnetism
Magnetic states	altermagnetism antiferromagnetism ferrimagnetism ferromagnetism superferromagnetism ferromagnetic superconductor helimagnetism metamagnetism mictomagnetism spin glass amorphous magnetism spin ice