Теория кристаллического поля
В молекулярной физике теория кристаллического поля ( CFT ) описывает разрыв выродий электронных орбитальных состояний, обычно D или F -орбиталей, из -за статического электрического поля, создаваемого окружающим распределением заряда (соседей по анион). Эта теория была использована для описания различных спектроскопий переходных металлов координационных комплексов , в частности, оптических спектра (цвета). CFT успешно учитывает некоторые магнитные свойства, цвета , гидратации энтальпии и шпинельные структуры комплексов переходных металлов, но не пытается описать связь. CFT был разработан физиком Гансом Бет [ 1 ] и Джон Хасбрук Ван Влек [ 2 ] в 1930 -х годах. Впоследствии CFT был в сочетании с молекулярной орбитальной теорией, чтобы сформировать более реалистичную и сложную теорию лиганда (LFT), которая дает представление о процессе химической связи в комплексах переходных металлов. CFT может быть осложнен в дальнейшем путем нарушения предположений, сделанных из относительных энергий орбитальных металлов и лиганда, требующих использования инвертированного лигандского поля (ILFT), чтобы лучше описать связь.
Обзор
[ редактировать ]Согласно теории кристаллического поля, взаимодействие между переходным металлом и лигандами вытекает из притяжения между положительно заряженным металлическим катионом и отрицательным зарядом на не связанных электронах лиганда. Теория разрабатывается путем рассмотрения энергетических изменений пяти вырожденных d -орбиталей после того, как они окружены множеством точечных зарядов, состоящих из лигандов. По мере приближения лиганда иона металла, электроны из лиганда будут ближе к некоторым из D -орбиталей и дальше от других, что вызывает потерю дегенерации. Электроны в D -орбиталях и в лиганде отталкивают друг друга из -за отталкивания между такими же зарядами. Таким образом, D -электроны ближе к лигандам будут иметь более высокую энергию, чем те, которые далее, что приводит к расщеплению D -орбиталей энергии. На это расщепление влияет следующие факторы:
- природа металлического иона.
- Металл по сравнению с окислением. Более высокое состояние окисления приводит к большему расщеплению по сравнению с сферическим полем.
- Расположение лигандов вокруг металлического иона.
- Координационный номер металла (то есть тетраэдрический, октаэдльный ...)
- Природа лигандов, окружающих металлический ион. Чем сильнее эффект лигандов, тем больше разница между группами с высокой и низкой энергией .
Наиболее распространенным типом комплекса является октаэдрический , в котором шесть лигандов образуют вершины октаэдра вокруг иона металла. В октаэдрической симметрии D -орбитали разделяются на два набора с разницей в энергии, Δ OCT ( параметр расщепления кристаллического поля , также обычно обозначаемый 10 DQ в течение десяти раз превышает «дифференциал кванта» [ 3 ] [ 4 ] ) там, где d xy , d xz и d -yz орбитали будут ниже по энергии, чем d z 2 и д х 2 - и 2 , который будет иметь более высокую энергию, потому что первая группа находится дальше от лигандов, чем последняя, и поэтому испытывает меньшее отталкивание. нижней энергией в совокупности называются T 2G , а две более энергичные орбитали как e G. Три орбитали с этикетки основаны на теории симметрии : они являются названиями неприводимых представлений октаэдрической точечной группе , х . о Эти молекулярной о -вращаться.
Тетраэдрические комплексы являются вторым наиболее распространенным типом; Здесь четыре лиганда образуют тетраэдр вокруг иона металла. В расщеплении тетраэдрического кристаллического поля D -орбитали снова разделяются на две группы, с разницей в энергии Δ Tet . Нижние энергетические орбитали будут D z 2 и д х 2 - и 2 и более высокие энергетические орбитали будут D XY , D XZ и D YZ - напротив октаэдрического случая. Кроме того, поскольку лигандные электроны в тетраэдрической симметрии не ориентированы непосредственно на D -орбитали, расщепление энергии будет ниже, чем в октаэдрическом случае. Квадратная плоская и другие сложные геометрии также могут быть описаны CFT.
Размер зазора δ между двумя или более наборами орбиталей зависит от нескольких факторов, включая лиганды и геометрию комплекса. Некоторые лиганды всегда дают небольшое значение δ, в то время как другие всегда дают большое расщепление. Причины этого могут быть объяснены теорией поля лиганда . Спектрохимический сериал представляет собой эмпирически из списка лигандов, упорядоченных размером расщепления, который они производят (малый δ до больших Δ; см. Также эту таблицу ):
я − < Br − < С 2− < Scn − (S -Bonded) < cl − < № 3 − < N 3 − < F − < О − < C 2 O 4 2− < H 2 o < ncs − (N-bonded) < 3 cn < ch phen < nh 3 < en < 2,2'-бипиридин < py < no 2 − < PPH 3 < CN − < Что .
Полезно отметить, что лиганды, производящие наиболее расщепление,-это те, которые могут вовлечь металл для лиганда .
Состояние окисления металла также способствует размеру Δ между высокими и низкими уровнями энергии. По мере увеличения уровня окисления для данного металла величина Δ увеличивается. средний 3+ Комплекс будет иметь больше Δ, чем v 2+ комплекс для данного набора лигандов, так как разница в плотности заряда позволяет лигандам быть ближе к V 3+ ион, чем на V 2+ ион Меньшее расстояние между лигандом и ионом металла приводит к большему Δ, потому что лиганд и металлические электроны ближе друг к другу и, следовательно, отталкивают больше.
Высокий и низкий спин
[ редактировать ]
Лиганды, которые вызывают большое расщепление δ D -орбиталей, называются лигандами сильного поля, такими как CN − и co из спектрохимической серии . В комплексах с этими лигандами неблагоприятно помещать электроны на орбитали с высокой энергией. Следовательно, нижние энергетические орбитали полностью заполнены до того, как популяция верхних наборов начинается в соответствии с принципом Aufbau . Такие комплексы называются «низким спином». Например, № 2 − является сильным лигандом и производит большой Δ. Октаэдрический ион [Fe (№ 2 ) 6 ] 3− , который имеет 5 D -электронов, будет иметь октаэдрическую диаграмму расщепления, показанную справа со всеми пятью электронами на T 2 G. уровне Таким образом, это состояние спина не следует правилу Хунда .

И наоборот, лиганды (как я − и бр − ), которые вызывают небольшое расщепление Δ d -орбиталей , называются лигандами слабых полетов. В этом случае легче положить электроны в более высокий набор энергии орбиталей, чем положить два в одну и ту же орбиталь с низким энергопотреблением, потому что два электрона в одной и той же орбитальной отталкивают друг друга. Таким образом, один электрон помещается в каждый из пяти D -орбиталей в соответствии с правилом Hund, и комплексы «высокого спина» образуются до того, как произойдет любое спаривание. Например, Br − является слабым полевым лигандом и производит небольшой Δ OCT . Итак, ион [ 6 февраля ] 3− , опять же с пятью D -электронами, будет иметь октаэдрическую диаграмму расщепления, где все пять орбиталей по одному.
Для того чтобы с низким расщеплением вращения произошло, стоимость энергии размещения электрона в и без того пожилой орбитал должна быть меньше, чем стоимость размещения дополнительного электрона в E -g Orbital по энергетической стоимости Δ. Как отмечалось выше, E G относится к D Z. 2 и д х 2 - и 2 которые выше по энергии выше, чем T 2G в октаэдрических комплексах. Если энергия, необходимая для соединения двух электронов, превышает Δ, то затраты энергии размещения электрона в E G , происходит высокое расщепление вращения.
Энергия расщепления кристаллического поля для комплексов тетраэдрических металлов (четыре лиганда) называется Δ TET и примерно равна 4/9Δ OCT (для того же металла и того же лигандов). Следовательно, энергия, необходимая для соединения двух электронов, обычно выше, чем энергия, необходимая для размещения электронов на орбиталях с более высокой энергией. Таким образом, тетраэдрические комплексы обычно высокие.
Использование этих диаграмм расщепления может помочь в прогнозировании магнитных свойств координационных соединений. Соединение, которое имеет непарные электроны в его диаграмме расщепления, будет парамагнитным и будет привлекать магнитными полями, в то время как соединение, в котором отсутствуют непарные электроны на его диаграмме расщепления, будет диамагнитным и будет слабо отталкиваться магнитным полем.
Энергия стабилизации
[ редактировать ]Энергия стабилизации кристаллического поля (CFSE) - это стабильность, возникающая в результате размещения иона переходного металла в кристаллическом поле, генерируемом набором лигандов. Это возникает из -за того, что, когда D -орбитали разделяются на поле лиганда (как описано выше), некоторые из них становятся ниже по энергии, чем раньше, в отношении сферического поля, известного как барицентр, в котором все пять d -орбиталей вырождены. Например, в октаэдрическом случае набор T 2G становится ниже по энергии, чем орбитали в барицентре. В результате этого, если есть какие -либо электроны, занимающие эти орбитали, ион металла более стабилен в поле лиганда относительно барицентра по количеству, известному как CFSE. И наоборот, e g -орбитали (в октаэдрическом случае) выше по энергии, чем в барицентре, поэтому размещение электронов в них уменьшает количество CFSE.

Если расщепление D -орбиталей в октаэдрическом поле составляет Δ OCT , три орбитали T 2G стабилизируются относительно барицентра 2 / 5 Δ oct , а e g орбитали дестабилизируются 3 / 5 Δ Oct. Как примеры, рассмотрим два D 5 Конфигурации показаны дальше вверх по странице. Пример с низким путем (вверху) имеет пять электронов на орбиталях T 2G , поэтому общий CFSE составляет 5 x 2 / 5 Δ oct = 2Δ oct . В примере с высокой (нижней), CFSE равен (3 x 2 / 5 Δ oct ) - (2 x 3 / 5 Δ oct ) = 0 - В этом случае стабилизация, генерируемая электронами в нижних орбиталях, отменяется путем дестабилизирующего эффекта электронов на верхних орбиталях.
Оптические свойства
[ редактировать ]Оптические свойства (детали спектров поглощения и излучения) многих координационных комплексов могут быть объяснены теорией кристаллического поля. Часто, однако, более глубокие цвета металлических комплексов возникают из-за более интенсивных возбуждений переноса заряда . [ 5 ]
Геометрия и диаграммы расщепления
[ редактировать ]| Имя | Форма | Энергетическая диаграмма |
|---|---|---|
| Октаэдральный |  |
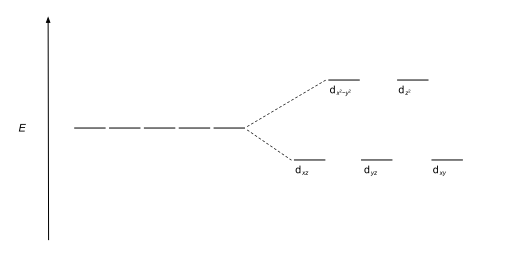 |
| Пентагональный бипирамидальный | 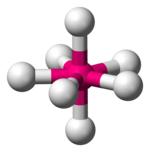 |
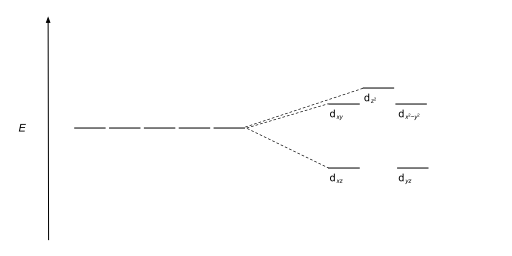 |
| Квадратный антипризматический | 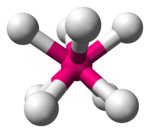 |
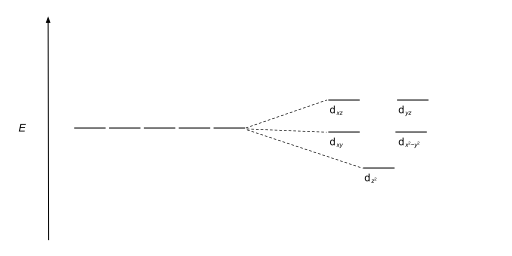 |
| Квадратный плоский |  |
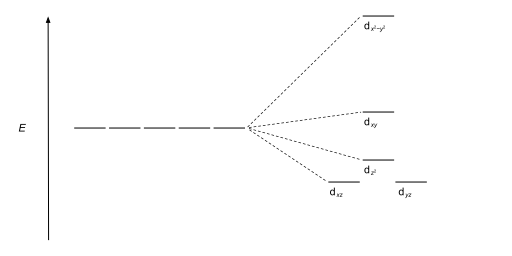 |
| Квадратный пирамидал | 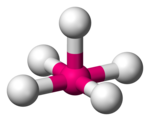 |
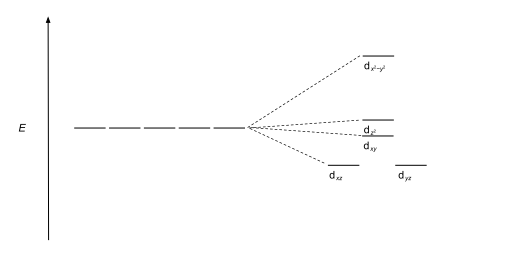 |
| Тетраэдрический |  |
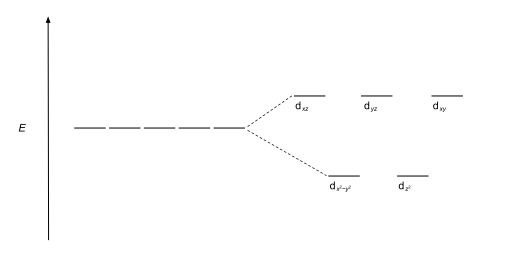 |
| Тригональный бипирамидальный |  |
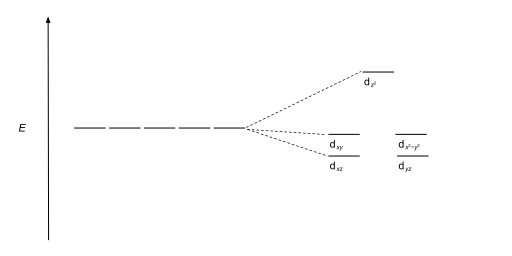 |
Смотрите также
[ редактировать ]- Аномалия Шоттки -низкотемпературная всплеск тепла, наблюдаемая в материалах, содержащих высокие спинные магнитные примеси, часто из-за расщепления кристаллического поля
- Теория поля лиганда
- Теория молекулярной орбитальной
Ссылки
[ редактировать ]- ^ Бет, Х. (1929). «Раздел разделен в кристаллах». Анналы физики (на немецком языке). 395 (2): 133–208. Bibcode : 1929anp ... 395..133b . Doi : 10.1002/andp.19293950202 . ISSN 1521-3889 .
- ^ Ван Влек, Дж. (1932). «Теория изменений в парамагнитной анизотропии среди различных солей железной группы». Физический обзор . 41 (2): 208–215. Bibcode : 1932phrv ... 41..208V . doi : 10.1103/physrev.41.208 .
- ^ Пенни, Уильям Дж.; Шлапп, Роберт (1932). «Влияние кристаллических полей на восприимчивости солей парамагнитных ионов. I. редкоземельные земли, особенно PR и ND». Физический обзор . 41 (2): 194–207. Bibcode : 1932phrv ... 41..194p . doi : 10.1103/physrev.41.194 . ISSN 0031-899X .
- ^ Шлапп, Роберт; Пенни, Уильям Г. (1932). «Влияние кристаллических полей на восприимчивость солей парамагнитных ионов. II. Железная группа, особенно Ni, Cr и Co». Физический обзор . 42 (5): 666–686. Bibcode : 1932phrv ... 42..666s . doi : 10.1103/physrev.42.666 . ISSN 0031-899X . \
- ^ Gl miessler и da tarr «неорганическая химия» 2 -е изд. (Prentice Hall 1999), с.379 ISBN 0-13-841891-8 .
Дальнейшее чтение
[ редактировать ]- Housecroft, CE; Sharpe, AG (2004). Неорганическая химия (2 -е изд.). Прентис Холл. ISBN 978-0-13-039913-7 .
- Мисслер, Гл; Tarr, DA (2003). Неорганическая химия (3 -е изд.). Пирсон Прентис Холл. ISBN 978-0-13-035471-6 .
- Оргель, Лесли Э. (1960). Введение в химию переходного металла: теория лиганда . Метуэн. ISBN 978-0416634402 .
- Шрайвер, DF; Аткинс, PW (2001). Неорганическая химия (4 -е изд.). Издательство Оксфордского университета. С. 227–236. ISBN 978-0-8412-3849-7 .
- Сильберберг, Мартин С. (2006). Химия: молекулярный характер материи и изменений (4 -е изд.). Нью -Йорк: McGraw Hill Company. С. 1028–1034 . ISBN 978-0-8151-8505-5 .
- Зумдаль, Стивен С. (2005). Химические принципы (5 -е изд.). Houghton Mifflin Company. С. 550–551, 957–964 . ISBN 978-0-669-39321-7 .
Внешние ссылки
[ редактировать ]- Теория кристаллического поля, метод жесткого связывания и эффект Jahn-Teller у E. Pavarini, E. Koch, F. Anders и M. Jarrell (Eds.): Коррелированные электроны: от моделей к материалам, Jülich 2012, ISBN 978-3-89336-796-2