Группа точек

Цветок Bauhinia blakeana на флаге региона Гонконг имеет симметрию C ₅ ; звезда на каждом лепестке имеет симметрию D ₅ .	Символ Инь и Ян имеет _{C 2} геометрию симметрии с инвертированными цветами.

В геометрии группа точек — это математическая группа операций симметрии ( изометрий в евклидовом пространстве ), которые имеют фиксированную точку общую евклидова . Началом координат пространства обычно считается фиксированная точка, и каждая точечная группа в размерности d является тогда подгруппой ортогональной группы O( d ). Группы точек используются для описания симметрии геометрических фигур и физических объектов, таких как молекулы .

Каждую группу точек можно представить как наборы ортогональных матриц M , которые преобразуют точку x в точку y согласно у = Mx . Каждый элемент точечной группы является либо = 1 ) , вращением (определитель M либо отражением или неправильным вращением (определитель M = −1 ).

Геометрические симметрии кристаллов описываются пространственными группами , которые допускают переводы и содержат точечные группы в качестве подгрупп. Дискретные точечные группы в более чем одном измерении входят в бесконечные семейства, но из кристаллографической теоремы ограничения и одной из теорем Бибербаха каждое число измерений имеет только конечное число точечных групп, которые симметричны над некоторой решеткой или сеткой с этим количеством измерений. . Это кристаллографические точечные группы .

Киральные и ахиральные точечные группы, группы отражений

Точечные группы можно разделить на киральные (или чисто вращательные) группы и ахиральные группы. ^[1]Киральные группы являются подгруппами специальной ортогональной группы SO( d ): они содержат только ортогональные преобразования, сохраняющие ориентацию, т. е. преобразования определителя +1. Ахиральные группы содержат также преобразования определителя −1. В ахиральной группе преобразования, сохраняющие ориентацию, образуют (киральную) подгруппу индекса 2.

Конечные группы Кокстера или группы отражений — это точечные группы, которые создаются исключительно набором отражающих зеркал, проходящих через одну и ту же точку. Группа Кокстера ранга n имеет n зеркал и представлена диаграммой Кокстера – Дынкина . Обозначение Коксетера предлагает обозначения в квадратных скобках, эквивалентные диаграмме Кокстера, с символами разметки для групп точек вращения и других субсимметрий. Группы отражения обязательно ахиральны (за исключением тривиальной группы, содержащей только единичный элемент).

Список групп точек

Одно измерение

Есть только две одномерные точечные группы: группа единиц и группа отражения.

Группа	Коксетер	Диаграмма Кокстера	Заказ	Описание
C_С1	[ ] ⁺		1	личность
Д ₁	[ ]		2	группа отражения

Два измерения

Группы точек в двух измерениях , иногда называемые группами розеток .

Они делятся на два бесконечных семейства:

Циклические группы C _n групп n -кратного вращения
Группы диэдра D _{n n} -кратных групп вращения и отражения

Применение кристаллографической ограничительной теоремы ограничивает n значениями 1, 2, 3, 4 и 6 для обоих семейств, что дает 10 групп.

Группа	Международный	Орбифолд	Коксетер	Заказ	Описание
С _н	н	n •	[ н ] ⁺	н	циклические: n -кратные вращения; абстрактная группа Z _n , группа целых чисел при сложении по модулю n
Д _н	нм	* n •	[ н ]	22н	двугранный: циклический с отражениями; абстрактная группа Dih _n , группа диэдра

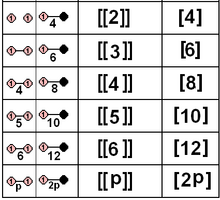
Подмножество чисто отражающих точечных групп, определяемое 1 или 2 зеркалами, также может быть задано их группой Кокстера и связанными с ней многоугольниками. К ним относятся 5 кристаллографических групп. Симметрию отражающих групп можно удвоить с помощью изоморфизма , отображая оба зеркала друг на друга с помощью биссектрисы, удваивая порядок симметрии.

Светоотражающий						Вращательный			Связанный многоугольники
Группа	Группа Коксетера		Диаграмма Кокстера		Заказ	Подгруппа	Коксетер	Заказ	Связанный многоугольники
Д ₁	А ₁	[ ]			2	C_С1	[] ⁺	1	достаточно
D_Д2	А ₁²	[2]			4	С ₂	[2] ⁺	2	прямоугольник
Д ₃	A_А2	[3]			6	С ₃	[3] ⁺	3	равносторонний треугольник
Д ₄	БК ₂	[4]			8	С ₄	[4] ⁺	4	квадрат
Д ₅	Ч ₂	[5]			10	C_С5	[5] ⁺	5	правильный пятиугольник
Д ₆	Г ₂	[6]			12	C_С6	[6] ⁺	6	правильный шестиугольник
Д _н	я ₂ ( н )	[ н ]			22н	С _н	[ н ] ⁺	н	правильный многоугольник
D ₂×2	А ₁²×2	[[2]] = [4]		=	8
D ₃×2	A ₂×2	[[3]] = [6]		=	12
D ₄×2	BC ₂×2	[[4]] = [8]		=	16
D ₅×2	H ₂×2	[[5]] = [10]		=	20
D ₆×2	G ₂×2	[[6]] = [12]		=	24
D _n×2	Я ₂ ( п )×2	[[ п ]] = [ 2n ]		=	4 н

Три измерения

Точечные группы в трех измерениях , иногда называемые молекулярными точечными группами из-за их широкого использования при изучении симметрии молекул .

Они входят в 7 бесконечных семейств осевых групп (также называемых призматическими) и 7 дополнительных многогранных групп (также называемых Платоновыми). В Шёнфлиса обозначениях

Осевые группы: C _n , S _{2 n} , C _{n h} , C _{n v} , D _n , D _{n d} , D _{n h}
Полиэдральные группы : Т, Т _д , Т _ч , О, О _ч , I, I _ч

Применение кристаллографической теоремы ограничения к этим группам дает 32 кристаллографические точечные группы .

Фундаментальные области четных/нечетных цветов отражающих групп
С _{1 в} Заказ 2	С _2В Заказ 4	С _3В Заказ 6	С _4В Заказать 8	С _5В Заказать 10	С _6в Заказ 12	...

Д _{1 час} Заказ 4	Д _{2 часа} Заказать 8	Д _{3 часа} Заказ 12	Д _{4 часа} Заказ 16	Д _5ч Заказать 20	Д _6ч Заказ 24	...

Т _д Заказ 24	Ой Заказ 48	I _h Заказать 120

Международный ^*	Гео ^[2]	Орбифолд	Шенфлис	Коксетер	Заказ
1	1	1	C_С1	[ ] ⁺	1
1	22	×1	С _я = S ₂	[2 ⁺,2 ⁺]	2
2 = м	1	*1	С _с = С _1v = С _1h	[ ]	2
2 3 4 5 6 н	2 3 4 5 6 н	22 33 44 55 66 пп	С ₂ С ₃ С ₄ C_С5 C_С6 С _н	[2] ⁺ [3] ⁺ [4] ⁺ [5] ⁺ [6] ⁺ [н] ⁺	2 3 4 5 6 н
мм2 3m 4 мм 5 м 6 мм н мм нм	2 3 4 5 6 н	22 33 44 55 66 нн	С _2В С _3В С _4В С _5В С _6в С _{н в}	[2] [3] [4] [5] [6] [ н ]	4 6 8 10 12 22н
2/м 6 4/м 10 6/м н /м 22н	2 2 3 2 4 2 5 2 6 2 № 2	2* 3* 4* 5* 6* н *	С _{2 часа} С _{3 часа} С _{4 часа} С _5ч С _{6 часов} С _{н ч}	[2,2 ⁺] [2,3 ⁺] [2,4 ⁺] [2,5 ⁺] [2,6 ⁺] [2,н ⁺]	4 6 8 10 12 22н
4 3 8 5 12 22н н	4 2 6 2 8 2 10 2 12 2 2n2n2	2× 3× 4× 5× 6× n ×	С ₄ S_S6 С ₈ С ₁₀ С ₁₂ С _{2 н}	[2 ⁺,4 ⁺] [2 ⁺,6 ⁺] [2 ⁺,8 ⁺] [2 ⁺,10 ⁺] [2 ⁺,12 ⁺] [2 ⁺,2 н ⁺]	4 6 8 10 12 22н

Международный	Гео	Орбифолд	Шенфлис	Коксетер	Заказ
222 32 422 52 622 № 22 нет 2	2 2 3 2 4 2 5 2 6 2 нет 2	222 223 224 225 226 22 н.	D_Д2 Д ₃ Д ₄ Д ₅ Д ₆ Д _н	[2,2] ⁺ [2,3] ⁺ [2,4] ⁺ [2,5] ⁺ [2,6] ⁺ [2, н ] ⁺	4 6 8 10 12 22н
М-м-м 6 м2 4/ммм 10 м2 6/ммм н /ммм 2 нм2	2 2 3 2 4 2 5 2 6 2 № 2	222 223 224 225 226 22 н.	Д _{2 часа} Д _{3 часа} Д _{4 часа} Д _5ч Д _6ч Д _{н ч}	[2,2] [2,3] [2,4] [2,5] [2,6] [2, н ]	8 12 16 20 24 4 н
4 2м 3 m 8 2м 55м 12 2м 2 н 2 м нм	4 2 6 2 8 2 10 2 12 2 № 2	22 23 24 25 26 2 н	Д _2д Д _3д Д _4д Д _5д Д _6д Д _{н д}	[2 ⁺,4] [2 ⁺,6] [2 ⁺,8] [2 ⁺,10] [2 ⁺,12] [2 ⁺, 2н ]	8 12 16 20 24 4 н
23	3 3	332	Т	[3,3] ⁺	12
m 3	4 3	3*2	Т _ч	[3 ⁺,4]	24
4 3м	3 3	*332	Т _д	[3,3]	24
432	4 3	432	ТО	[3,4] ⁺	24
м 3 м	4 3	*432	Ой	[3,4]	48
532	5 3	532	я	[3,5] ⁺	60
5 3 м	5 3	*532	I _h	[3,5]	120

(*) Когда записи Intl дублируются, первая предназначена для четного n , вторая — для нечетного n .

Группы отражения

Группы точек отражения, определяемые от 1 до 3 зеркальных плоскостей, также могут быть заданы их группой Кокстера и соответствующими многогранниками. Группу [3,3] можно удвоить, записать как [[3,3]], отображая первое и последнее зеркала друг на друга, удваивая симметрию до 48 и изоморфную группе [4,3].

Шенфлис	Группа Коксетера			Заказ	Связанные регулярные и призматические многогранники
Т _д	A_А3	[3,3]		24	тетраэдр
Т _d ×Dih ₁ = О _час	А ₃ ×2 = ВС ₃	[[3,3]] = [4,3]	=	48	звездчатый октаэдр
Ой	БК ₃	[4,3]		48	куб , октаэдр
I _h	H_H3	[5,3]		120	икосаэдр , додекаэдр
Д _{3 часа}	A ₂×A ₁	[3,2]		12	треугольная призма
Д _3ч ×Дих ₁ = Д _6ч	A ₂×A ₁×2	[[3],2]	=	24	шестиугольная призма
Д _{4 часа}	BC ₂×A ₁	[4,2]		16	квадратная призма
Д _4ч ×Дих ₁ = Д _8ч	BC ₂×A ₁×2	[[4],2] = [8,2]	=	32	восьмиугольная призма
Д _5ч	H ₂×A ₁	[5,2]		20	пятиугольная призма
Д _6ч	G ₂×A ₁	[6,2]		24	шестиугольная призма
Д _{н ч}	Я ₂ ( н )×А ₁	[ н ,2]		4 н	n- угольная призма
Д _{н час} ×Dih ₁ = Д _{2 н час}	я ₂ ( п )×А ₁ ×2	[[ п ],2]	=	8 год нашей эры
Д _{2 часа}	А ₁³	[2,2]		8	кубовидный
D _2h×Dih ₁	А ₁³×2	[[2],2] = [4,2]	=	16
D _2h ×Dih ₃ = О _час	А ₁³×6	[3[2,2]] = [4,3]	=	48
С _3В	A_А2	[1,3]		6	осоэдр
С _4В	БК ₂	[1,4]		8
С _5В	Ч ₂	[1,5]		10
С _6в	Г ₂	[1,6]		12
С _нв	я ₂ ( н )	[1, н ]		22н
C _{n v} ×Dih ₁ = C _{2 n v}	Я ₂ ( п )×2	[1,[ п ]] = [1,2 п ]	=	4 н
С _{2 в}	А ₁²	[1,2]		4
C _2v×Dih ₁	А ₁²×2	[1,[2]]	=	8
С _с	А ₁	[1,1]		2

Четыре измерения

Четырехмерные точечные группы (хиральные и ахиральные) перечислены у Конвея и Смита. ^[1] Раздел 4, Таблицы 4.1–4.3.

В следующем списке приведены четырехмерные группы отражений (за исключением тех, которые оставляют фиксированным подпространство и, следовательно, являются группами отражений меньшей размерности). Каждая группа определяется как группа Коксетера , и, как и многогранные группы 3D, ее можно назвать по связанному с ней выпуклому правильному 4-многограннику . Связанные чисто вращательные группы существуют для каждой с половиной порядка и могут быть представлены скобочной нотацией Кокстера с показателем «+», например [3,3,3] ⁺ имеет три точки трехкратного вращения и порядок симметрии 60. Симметричные группы спереди назад, такие как [3,3,3] и [3,4,3], могут быть удвоены, что показано в виде двойных скобок в обозначениях Коксетера, например [[3 ,3,3]] с его порядком, увеличенным вдвое до 240.

Группа Кокстера / обозначения			Заказ	Связанные многогранники
A ₄	[3,3,3]		120	5-клеточный
A ₄×2	[[3,3,3]]		240	5-клеточное двойное соединение
БК ₄	[4,3,3]		384	16 ячеек / тессеракт
Д ₄	[3 ^1,1,1]		192	демитэссерактический
Д ₄ ×2 = БК ₄	<[3,3 ^1,1]> = [4,3,3]	=	384
Д ₄ × 6 = Ф ₄	[3[3 ^1,1,1]] = [3,4,3]	=	1152
F_F4	[3,4,3]		1152	24-ячеечный
F ₄×2	[[3,4,3]]		2304	24-элементное двойное соединение
Ч ₄	[5,3,3]		14400	120 ячеек / 600 ячеек
A ₃×A ₁	[3,3,2]		48	тетраэдрическая призма
A ₃×A ₁×2	[[3,3],2] = [4,3,2]	=	96	октаэдрическая призма
BC ₃×A ₁	[4,3,2]		96	октаэдрическая призма
H ₃×A ₁	[5,3,2]		240	икосаэдральная призма
A ₂×A ₂	[3,2,3]		36	дуопризма
A ₂×BC ₂	[3,2,4]		48
A ₂×H ₂	[3,2,5]		60
A ₂×G ₂	[3,2,6]		72
BC ₂×BC ₂	[4,2,4]		64
БК ₂²×2	[[4,2,4]]		128
BC ₂×H ₂	[4,2,5]		80
BC ₂×G ₂	[4,2,6]		96
H ₂×H ₂	[5,2,5]		100
H ₂×G ₂	[5,2,6]		120
G ₂×G ₂	[6,2,6]		144
Я ₂ ( п ) × Я ₂ ( q )	[ п ,2, q ]		4 шт.
Я ₂ (2 п )×I ₂ ( q )	[[ п ],2, q ] = [2 п ,2, q ]	=	8 кв.м.
I ₂ (2 п )×I ₂ (2 q )	[[ п ]],2,[[ q ]] = [2 п ,2,2 q ]	=	16 кв.м.
я ₂ ( п ) ²×2	[[ п ,2, п ]]		8 р. ²
Я ₂ ( 2п ) ²×2	[[[ p ]],2,[ p ]]] = [[2 p ,2,2 p ]]	=	32 р. ²
A ₂×A ₁×A ₁	[3,2,2]		24
BC ₂×A ₁×A ₁	[4,2,2]		32
H ₂×A ₁×A ₁	[5,2,2]		40
G ₂×A ₁×A ₁	[6,2,2]		48
Я ₂ ( п )×А ₁ ×А ₁	[ п ,2,2]		8 р.
Я ₂ (2 п )×А ₁ ×А ₁ ×2	[[ п ],2,2] = [2 п ,2,2]	=	16 р.
Я ₂ ( п )×А ₁²×2	[ п ,2,[2]] = [ п ,2,4]	=	16 р.
Я ₂ (2 п )×А ₁²×4	[[ п ]],2,[[2]] = [2 п ,2,4]	=	32 р.
A ₁×A ₁×A ₁×A ₁	[2,2,2]		16	4- ортотоп
А ₁²×A ₁×A ₁×2	[[2],2,2] = [4,2,2]	=	32
А ₁²×A ₁²×4	[[2]],2,[[2]] = [4,2,4]	=	64
А ₁³×A ₁×6	[3[2,2],2] = [4,3,2]	=	96
А ₁⁴×24	[3,3[2,2,2]] = [4,3,3]	=	384

Пять измерений

Конечный изоморфизм и соответствия

В следующей таблице представлены пятимерные группы отражений (за исключением групп отражений более низкой размерности), перечисленные как группы Кокстера . Связанные киральные группы существуют для каждой с половиной порядка и могут быть представлены скобочной записью Кокстера с показателем «+», например [3,3,3,3] ⁺ имеет четыре точки тройного вращения и порядок симметрии 360.

Группа Кокстера / обозначения			Заказ	Связанные регулярные и призматические многогранники
A_А5	[3,3,3,3]		720	5-симплекс
A ₅×2	[[3,3,3,3]]		1440	5-симплексное двойное соединение
БК ₅	[4,3,3,3]		3840	5-куб , 5-ортоплекс
Д ₅	[3 ^2,1,1]		1920	5-демикуб
D ₅×2	<[3,3,3 ^1,1]>	=	3840
A ₄×A ₁	[3,3,3,2]		240	5-ячеечная призма
A ₄×A ₁×2	[[3,3,3],2]		480
BC ₄×A ₁	[4,3,3,2]		768	тессерактовая призма
F ₄×A ₁	[3,4,3,2]		2304	24-ячеечная призма
F ₄×A ₁×2	[[3,4,3],2]		4608	24-ячеечная призма
H ₄×A ₁	[5,3,3,2]		28800	с 600 или 120 ячейками Призма
D ₄×A ₁	[3 ^1,1,1,2]		384	полудессерактная призма
A ₃×A ₂	[3,3,2,3]		144	дуопризма
A ₃×A ₂×2	[[3,3],2,3]		288
A ₃×BC ₂	[3,3,2,4]		192
A ₃×H ₂	[3,3,2,5]		240
A ₃×G ₂	[3,3,2,6]		288
А ₃ ×I ₂ ( п )	[3,3,2,п]		48 р
BC ₃×A ₂	[4,3,2,3]		288
BC ₃×BC ₂	[4,3,2,4]		384
BC ₃×H ₂	[4,3,2,5]		480
BC ₃×G ₂	[4,3,2,6]		576
до н.э. ₃ ×I ₂ ( п )	[4,3,2,п]		96 р
H ₃×A ₂	[5,3,2,3]		720
H ₃×BC ₂	[5,3,2,4]		960
H ₃×H ₂	[5,3,2,5]		1200
H ₃×G ₂	[5,3,2,6]		1440
Ч ₃ ×I ₂ ( п )	[5,3,2, п ]		240 р.
A ₃×A ₁²	[3,3,2,2]		96
BC ₃×A ₁²	[4,3,2,2]		192
H ₃×A ₁²	[5,3,2,2]		480
A_А2²×A ₁	[3,2,3,2]		72	дуопризма призма
A ₂×BC ₂×A ₁	[3,2,4,2]		96
A ₂×H ₂×A ₁	[3,2,5,2]		120
A ₂×G ₂×A ₁	[3,2,6,2]		144
БК ₂²×A ₁	[4,2,4,2]		128
BC ₂×H ₂×A ₁	[4,2,5,2]		160
BC ₂×G ₂×A ₁	[4,2,6,2]		192
Ч ₂²×A ₁	[5,2,5,2]		200
H ₂×G ₂×A ₁	[5,2,6,2]		240
Г ₂²×A ₁	[6,2,6,2]		288
Я ₂ ( п )×Я ₂ ( q )×А ₁	[ п ,2, д ,2]		8 кв.м.
A ₂×A ₁³	[3,2,2,2]		48
BC ₂×A ₁³	[4,2,2,2]		64
H ₂×A ₁³	[5,2,2,2]		80
G ₂×A ₁³	[6,2,2,2]		96
Я ₂ ( п )×А ₁³	[ п ,2,2,2]		16 р.
А ₁⁵	[2,2,2,2]		32	5- ортотоп
А ₁⁵×(2 ! )	[[2],2,2,2]	=	64
А ₁⁵×(2!×2 ! )	[[2]],2,[2],2]	=	128
А ₁⁵×(3 ! )	[3[2,2],2,2]	=	192
А ₁⁵×(3!×2 ! )	[3[2,2],2,[[2]]	=	384
А ₁⁵×(4 ! )	[3,3[2,2,2],2]]	=	768
А ₁⁵×(5 ! )	[3,3,3[2,2,2,2]]	=	3840

Шесть измерений

Конечный изоморфизм и соответствия

В следующей таблице представлены шестимерные группы отражений (за исключением групп отражений меньшей размерности), перечисленные как группы Кокстера . Связанные чисто вращательные группы существуют для каждой с половиной порядка и могут быть представлены скобочной нотацией Кокстера с показателем «+», например [3,3,3,3,3] ⁺ имеет пять точек тройного вращения и порядок симметрии 2520.

Группа Коксетера		Заказ	Связанные регулярные и призматические многогранники
А ₆	[3,3,3,3,3]	5040 (7!)	6-симплекс
A ₆×2	[[3,3,3,3,3]]	10080 (2×7!)	6-симплексное двойное соединение
до н.э. ₆	[4,3,3,3,3]	46080 (2 ⁶×6!)	6-куб , 6-ортоплекс
Д ₆	[3,3,3,3 ^1,1]	23040 (2 ⁵×6!)	6-демикуб
E_Е6	[3,3 ^2,2]	51840 (72×6!)	1 ₂₂, 2 ₂₁
A ₅×A ₁	[3,3,3,3,2]	1440 (2×6!)	5-симплексная призма
BC ₅×A ₁	[4,3,3,3,2]	7680 (2 ⁶×5!)	5-кубовая призма
D ₅×A ₁	[3,3,3 ^1,1,2]	3840 (2 ⁵×5!)	5-кубическая призма
А ₄ ×I ₂ ( п )	[3,3,3,2, п ]	240 р.	дуопризма
до н.э. ₄ ×I ₂ ( п )	[4,3,3,2, п ]	768 р.
Ф ₄ ×I ₂ ( п )	[3,4,3,2, п ]	2304 р
Ч ₄ ×I ₂ ( п )	[5,3,3,2, п ]	28800 р
Д ₄ ×I ₂ ( п )	[3,3 ^1,1,2, п ]	384 р.
A ₄×A ₁²	[3,3,3,2,2]	480
BC ₄×A ₁²	[4,3,3,2,2]	1536
F ₄×A ₁²	[3,4,3,2,2]	4608
H ₄×A ₁²	[5,3,3,2,2]	57600
D ₄×A ₁²	[3,3 ^1,1,2,2]	768
A_А3²	[3,3,2,3,3]	576
A ₃×BC ₃	[3,3,2,4,3]	1152
A ₃×H ₃	[3,3,2,5,3]	2880
БК ₃²	[4,3,2,4,3]	2304
BC ₃×H ₃	[4,3,2,5,3]	5760
H_H3²	[5,3,2,5,3]	14400
А ₃ ×I ₂ ( п )×А ₁	[3,3,2, п ,2]	96 р	дуопризма призма
БК ₃ ×I ₂ ( п )×А ₁	[4,3,2, п ,2]	192 стр.
Ч ₃ ×I ₂ ( п )×А ₁	[5,3,2, п ,2]	480 р.
A ₃×A ₁³	[3,3,2,2,2]	192
BC ₃×A ₁³	[4,3,2,2,2]	384
H ₃×A ₁³	[5,3,2,2,2]	960
Я ₂ ( п)×I ₂ ( q )×I ₂ (r)	[ п ,2, д ,2, р ]	8 рупий	триапризма
Я ₂ ( п )×Я ₂ ( q )×А ₁²	[ п ,2, д ,2,2]	16 кв.м.
Я ₂ ( п )×А ₁⁴	[ п ,2,2,2,2]	32 р.
А ₁⁶	[2,2,2,2,2]	64	6- ортотоп

Семь измерений

В следующей таблице приведены семимерные группы отражений (за исключением групп отражений более низкой размерности), перечисленные как группы Кокстера . Связанные киральные группы существуют для каждой с половиной порядка, определяемого четным числом отражений, и могут быть представлены скобочной записью Кокстера с показателем «+», например [3,3,3,3,3,3] ⁺ имеет шесть точек тройного вращения и порядок симметрии 20160.

Группа Коксетера		Заказ	Связанные многогранники
A ₇	[3,3,3,3,3,3]	40320 (8!)	7-симплекс
A ₇×2	[[3,3,3,3,3,3]]	80640 (2×8!)	7-симплексное двойное соединение
г. до н.э. ₇	[4,3,3,3,3,3]	645120 (2 ⁷×7!)	7-куб , 7-ортоплекс
D ₇	[3,3,3,3,3 ^1,1]	322560 (2 ⁶×7!)	7-демикуб
E ₇	[3,3,3,3 ^2,1]	2903040 (8×9!)	3 ₂₁, 2 ₃₁, 1 ₃₂
A ₆×A ₁	[3,3,3,3,3,2]	10080 (2×7!)
BC ₆×A ₁	[4,3,3,3,3,2]	92160 (2 ⁷×6!)
D ₆×A ₁	[3,3,3,3 ^1,1,2]	46080 (2 ⁶×6!)
E ₆×A ₁	[3,3,3 ^2,1,2]	103680 (144×6!)
А ₅ ×I ₂ ( п )	[3,3,3,3,2, п ]	1440 р
до н.э. ₅ ×I ₂ ( п )	[4,3,3,3,2, п ]	7680 р
Д ₅ ×I ₂ ( п )	[3,3,3 ^1,1,2, п ]	3840 р
A ₅×A ₁²	[3,3,3,3,2,2]	2880
BC ₅×A ₁²	[4,3,3,3,2,2]	15360
D ₅×A ₁²	[3,3,3 ^1,1,2,2]	7680
A ₄×A ₃	[3,3,3,2,3,3]	2880
A ₄×BC ₃	[3,3,3,2,4,3]	5760
A ₄×H ₃	[3,3,3,2,5,3]	14400
BC ₄×A ₃	[4,3,3,2,3,3]	9216
BC ₄×BC ₃	[4,3,3,2,4,3]	18432
BC ₄×H ₃	[4,3,3,2,5,3]	46080
H ₄×A ₃	[5,3,3,2,3,3]	345600
H ₄×BC ₃	[5,3,3,2,4,3]	691200
H ₄×H ₃	[5,3,3,2,5,3]	1728000
F ₄×A ₃	[3,4,3,2,3,3]	27648
F ₄×BC ₃	[3,4,3,2,4,3]	55296
F ₄×H ₃	[3,4,3,2,5,3]	138240
D ₄×A ₃	[3 ^1,1,1,2,3,3]	4608
D ₄×BC ₃	[3,3 ^1,1,2,4,3]	9216
D ₄×H ₃	[3,3 ^1,1,2,5,3]	23040
А ₄ ×И ₂ ( п )×А ₁	[3,3,3,2, п ,2]	480 р.
до н.э. ₄ ×I ₂ ( п ) × А ₁	[4,3,3,2, п ,2]	1536 р.
Д ₄ ×И ₂ ( п )×А ₁	[3,3 ^1,1,2, п ,2]	768 р.
Ф ₄ ×И ₂ ( п )×А ₁	[3,4,3,2, п ,2]	4608 р
Ч ₄ ×I ₂ ( п )×А ₁	[5,3,3,2, п ,2]	57600 р
A ₄×A ₁³	[3,3,3,2,2,2]	960
BC ₄×A ₁³	[4,3,3,2,2,2]	3072
F ₄×A ₁³	[3,4,3,2,2,2]	9216
H ₄×A ₁³	[5,3,3,2,2,2]	115200
D ₄×A ₁³	[3,3 ^1,1,2,2,2]	1536
A_А3²×A ₁	[3,3,2,3,3,2]	1152
A ₃×BC ₃×A ₁	[3,3,2,4,3,2]	2304
A ₃×H ₃×A ₁	[3,3,2,5,3,2]	5760
БК ₃²×A ₁	[4,3,2,4,3,2]	4608
BC ₃×H ₃×A ₁	[4,3,2,5,3,2]	11520
H_H3²×A ₁	[5,3,2,5,3,2]	28800
А ₃ ×I ₂ ( п )×I ₂ ( q )	[3,3,2, п , 2, q ]	96 кв.м.
до н.э. ₃ ×I ₂ ( п ) × I ₂ ( q )	[4,3,2, п , 2, q ]	192 кв.м.
ЧАС ₃ ×I ₂ ( п )×I ₂ ( q )	[5,3,2, п , 2, q ]	480 кв.м.
А ₃ ×I ₂ ( п )×А ₁²	[3,3,2, п ,2,2]	192 стр.
БК ₃ ×I ₂ ( п )×А ₁²	[4,3,2, п ,2,2]	384 р.
Ч ₃ ×I ₂ ( п )×А ₁²	[5,3,2, п ,2,2]	960 р.
A ₃×A ₁⁴	[3,3,2,2,2,2]	384
BC ₃×A ₁⁴	[4,3,2,2,2,2]	768
H ₃×A ₁⁴	[5,3,2,2,2,2]	1920
Я ₂ ( п )×I ₂ ( q )×I ₂ ( р )×A ₁	[ п ,2, д ,2, р ,2]	16 рупий
Я ₂ ( п )×Я ₂ ( q )×А ₁³	[ п ,2, д ,2,2,2]	32 кв.м.
Я ₂ ( п )×А ₁⁵	[ п ,2,2,2,2,2]	64 р
А ₁⁷	[2,2,2,2,2,2]	128

Восемь измерений

В следующей таблице приведены восьмимерные группы отражений (за исключением групп отражений более низкой размерности), перечисленные как группы Кокстера . Родственные киральные группы существуют для каждой с половиной порядка, определяемого четным числом отражений, и могут быть представлены скобочной записью Кокстера с показателем «+», например [3,3,3,3,3,3, 3] ⁺ имеет семь точек тройного вращения и порядок симметрии 181440.

Группа Коксетера		Заказ	Связанные многогранники
А ₈	[3,3,3,3,3,3,3]	362880 (9!)	8-симплекс
A ₈×2	[[3,3,3,3,3,3,3]]	725760 (2×9!)	8-симплексное двойное соединение
г. до н.э. ₈	[4,3,3,3,3,3,3]	10321920 (2 ⁸8!)	8-куб , 8-ортоплекс
Д ₈	[3,3,3,3,3,3 ^1,1]	5160960 (2 ⁷8!)	8-демикуб
E_Е8	[3,3,3,3,3 ^2,1]	696729600 (192×10!)	4 ₂₁, 2 ₄₁, 1 ₄₂
A ₇×A ₁	[3,3,3,3,3,3,2]	80640	7-симплексная призма
BC ₇×A ₁	[4,3,3,3,3,3,2]	645120	7-кубовая призма
D ₇×A ₁	[3,3,3,3,3 ^1,1,2]	322560	7-кубическая призма
E ₇×A ₁	[3,3,3,3 ^2,1,2]	5806080	3 ₂₁ призма, 2 ₃₁ призма, 1 ₄₂ призма
А ₆ ×I ₂ ( п )	[3,3,3,3,3,2, п ]	10080 р	дуопризма
до н.э. ₆ ×I ₂ ( п )	[4,3,3,3,3,2, п ]	92160 р
Д ₆ ×I ₂ ( п )	[3,3,3,3 ^1,1,2, п ]	46080 р
Е ₆ ×I ₂ ( п )	[3,3,3 ^2,1,2, п ]	103680 р
A ₆×A ₁²	[3,3,3,3,3,2,2]	20160
BC ₆×A ₁²	[4,3,3,3,3,2,2]	184320
D ₆×A ₁²	[3 ^3,1,1,2,2]	92160
E ₆×A ₁²	[3,3,3 ^2,1,2,2]	207360
A ₅×A ₃	[3,3,3,3,2,3,3]	17280
BC ₅×A ₃	[4,3,3,3,2,3,3]	92160
D ₅×A ₃	[3 ^2,1,1,2,3,3]	46080
A ₅×BC ₃	[3,3,3,3,2,4,3]	34560
BC ₅×BC ₃	[4,3,3,3,2,4,3]	184320
D ₅×BC ₃	[3 ^2,1,1,2,4,3]	92160
A ₅×H ₃	[3,3,3,3,2,5,3]
BC ₅×H ₃	[4,3,3,3,2,5,3]
D ₅×H ₃	[3 ^2,1,1,2,5,3]
А ₅ ×И ₂ ( п )×А ₁	[3,3,3,3,2, п ,2]
до н.э. ₅ ×I ₂ ( п ) × А ₁	[4,3,3,3,2, п ,2]
Д ₅ ×И ₂ ( п )×А ₁	[3 ^2,1,1,2, п ,2]
A ₅×A ₁³	[3,3,3,3,2,2,2]
BC ₅×A ₁³	[4,3,3,3,2,2,2]
D ₅×A ₁³	[3 ^2,1,1,2,2,2]
A ₄×A ₄	[3,3,3,2,3,3,3]
BC ₄×A ₄	[4,3,3,2,3,3,3]
D ₄×A ₄	[3 ^1,1,1,2,3,3,3]
F ₄×A ₄	[3,4,3,2,3,3,3]
H ₄×A ₄	[5,3,3,2,3,3,3]
BC ₄×BC ₄	[4,3,3,2,4,3,3]
D ₄×BC ₄	[3 ^1,1,1,2,4,3,3]
F ₄×BC ₄	[3,4,3,2,4,3,3]
H ₄×BC ₄	[5,3,3,2,4,3,3]
D ₄×D ₄	[3 ^1,1,1,2,3 ^1,1,1]
F ₄×D ₄	[3,4,3,2,3 ^1,1,1]
H ₄×D ₄	[5,3,3,2,3 ^1,1,1]
F ₄×F ₄	[3,4,3,2,3,4,3]
H ₄×F ₄	[5,3,3,2,3,4,3]
H ₄×H ₄	[5,3,3,2,5,3,3]
A ₄×A ₃×A ₁	[3,3,3,2,3,3,2]		дуопризма призмы
A ₄×BC ₃×A ₁	[3,3,3,2,4,3,2]
A ₄×H ₃×A ₁	[3,3,3,2,5,3,2]
BC ₄×A ₃×A ₁	[4,3,3,2,3,3,2]
BC ₄×BC ₃×A ₁	[4,3,3,2,4,3,2]
BC ₄×H ₃×A ₁	[4,3,3,2,5,3,2]
H ₄×A ₃×A ₁	[5,3,3,2,3,3,2]
H ₄×BC ₃×A ₁	[5,3,3,2,4,3,2]
H ₄×H ₃×A ₁	[5,3,3,2,5,3,2]
F ₄×A ₃×A ₁	[3,4,3,2,3,3,2]
F ₄×BC ₃×A ₁	[3,4,3,2,4,3,2]
F ₄×H ₃×A ₁	[3,4,2,3,5,3,2]
D ₄×A ₃×A ₁	[3 ^1,1,1,2,3,3,2]
D ₄×BC ₃×A ₁	[3 ^1,1,1,2,4,3,2]
D ₄×H ₃×A ₁	[3 ^1,1,1,2,5,3,2]
А ₄ ×I ₂ ( п ) × I ₂ ( q )	[3,3,3,2, п ,2, q ]		триапризма
BC ₄ ×I ₂ ( п ) × I ₂ ( q )	[4,3,3,2, п , 2, д]
F ₄ ×I ₂ ( п )×I ₂ ( q )	[3,4,3,2, п , 2, д]
ЧАС ₄ ×I ₂ ( п )×I ₂ ( q )	[5,3,3,2, п ,2,д]
Д ₄ ×I ₂ ( п )×I ₂ ( q )	[3 ^1,1,1,2, п ,2, q ]
А ₄ ×И ₂ ( п )×А ₁²	[3,3,3,2, п ,2,2]
до н.э. ₄ ×I ₂ ( п ) × А ₁²	[4,3,3,2, п ,2,2]
Ф ₄ ×И ₂ ( п )×А ₁²	[3,4,3,2, п ,2,2]
Ч ₄ ×I ₂ ( п )×А ₁²	[5,3,3,2, п ,2,2]
Д ₄ ×И ₂ ( п )×А ₁²	[3 ^1,1,1,2, п ,2,2]
A ₄×A ₁⁴	[3,3,3,2,2,2,2]
BC ₄×A ₁⁴	[4,3,3,2,2,2,2]
F ₄×A ₁⁴	[3,4,3,2,2,2,2]
H ₄×A ₁⁴	[5,3,3,2,2,2,2]
D ₄×A ₁⁴	[3 ^1,1,1,2,2,2,2]
А ₃ ×А ₃ ×I ₂ ( п )	[3,3,2,3,3,2, п ]
до н.э. ₃ ×А ₃ ×I ₂ ( п )	[4,3,2,3,3,2, п ]
ЧАС ₃ ×А ₃ ×I ₂ ( п )	[5,3,2,3,3,2, п ]
БК ₃ ×БК ₃ ×I ₂ ( п )	[4,3,2,4,3,2, п ]
ЧАС ₃ ×BC ₃ ×I ₂ ( п )	[5,3,2,4,3,2, п ]
ЧАС ₃ ×Ч ₃ ×I ₂ ( п )	[5,3,2,5,3,2, п ]
A ₃×A ₃×A ₁²	[3,3,2,3,3,2,2]
BC ₃×A ₃×A ₁²	[4,3,2,3,3,2,2]
H ₃×A ₃×A ₁²	[5,3,2,3,3,2,2]
BC ₃×BC ₃×A ₁²	[4,3,2,4,3,2,2]
H ₃×BC ₃×A ₁²	[5,3,2,4,3,2,2]
H ₃×H ₃×A ₁²	[5,3,2,5,3,2,2]
А ₃ ×I ₂ ( п ) × I ₂ ( q )× А ₁	[3,3,2, п ,2, д ,2]
БК ₃ ×I ₂ ( п )×I ₂ ( q )×А ₁	[4,3,2, п ,2, д ,2]
ЧАС ₃ ×I ₂ ( п )×I ₂ ( q )×А ₁	[5,3,2, п , 2, д , 2]
А ₃ ×I ₂ ( п )×А ₁³	[3,3,2, п ,2,2,2]
БК ₃ ×I ₂ ( п )×А ₁³	[4,3,2, п ,2,2,2]
Ч ₃ ×I ₂ ( п )×А ₁³	[5,3,2, п ,2,2,2]
A ₃×A ₁⁵	[3,3,2,2,2,2,2]
BC ₃×A ₁⁵	[4,3,2,2,2,2,2]
H ₃×A ₁⁵	[5,3,2,2,2,2,2]
Я ₂ ( п )×I ₂ ( q )×I ₂ ( р )×I ₂ ( s )	[ п ,2, д ,2, р ,2, с ]	16 мест
Я ₂ ( п )×I ₂ ( q )×I ₂ ( р )×A ₁²	[ п ,2, д ,2, р ,2,2]	32 рупии
Я ₂ ( п )×Я ₂ ( q )×А ₁⁴	[ п ,2, д ,2,2,2,2]	64 кв.м.
Я ₂ ( п )×А ₁⁶	[ п ,2,2,2,2,2,2]	128 стр.
А ₁⁸	[2,2,2,2,2,2,2]	256

См. также

Ссылки

^ Jump up to: ^а ^б Конвей, Джон Х .; Смит, Дерек А. (2003). О кватернионах и октонионах: их геометрия, арифметика и симметрия . АК Петерс. ISBN 978-1-56881-134-5 .
^ Кристаллографические пространственные группы в геометрической алгебре , Д. Хестенес и Дж. Холт, Журнал математической физики. 48, 023514 (2007) (22 страницы)

Дальнейшее чтение

HSM Coxeter (1995), Ф. Артур Шерк; Питер МакМаллен; Энтони К. Томпсон; Азия Ивик Вайс (ред.), Калейдоскопы: избранные сочинения HSM Коксетера , Wiley-Interscience Publication, ISBN 978-0-471-01003-6
- (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559–591]
HSM Коксетер ; WOJ Moser (1980), Генераторы и отношения для дискретных групп (4-е изд.), Нью-Йорк: Springer-Verlag
Н. В. Джонсон (2018), «Глава 11: Конечные группы симметрии», Геометрия и преобразования

Внешние ссылки

[Conway-Smith-1] Jump up to: ^а ^б Конвей, Джон Х .; Смит, Дерек А. (2003). О кватернионах и октонионах: их геометрия, арифметика и симметрия . АК Петерс. ISBN 978-1-56881-134-5 .

[2] Кристаллографические пространственные группы в геометрической алгебре , Д. Хестенес и Дж. Холт, Журнал математической физики. 48, 023514 (2007) (22 страницы)

[1]

[2]