Слышать форму барабана

Услышать форму барабана — значит вывести информацию о форме пластика из звука, который он издает, то есть из списка обертонов , с помощью математической теории.

«Можно ли услышать форму барабана?» — это название статьи Марка Каца в American Mathematical Monthly, опубликованной в 1966 году , которая сделала этот вопрос знаменитым, хотя эта конкретная формулировка принадлежит Липману Берсу . Подобные вопросы можно проследить вплоть до физика Артура Шустера в 1882 году. ^[1] За свою статью Кац был удостоен премии Лестера Р. Форда в 1967 году и премии Шовене в 1968 году. ^[2]

Частоты, на которых может вибрировать пластик, зависят от его формы. Уравнение Гельмгольца вычисляет частоты, если известна форма. Эти частоты являются в пространстве собственными значениями лапласиана . Главный вопрос заключается в том, можно ли предсказать форму, если известны частоты; например, треугольник Рело . можно ли таким образом распознать ^[3]Кац признал, что он не знает, могут ли две разные формы давать одинаковый набор частот. На вопрос о том, определяют ли частоты форму, в начале 1990-х годов Гордон, Уэбб и Вулперт наконец ответили отрицательно.

Официальное заявление [ править ]

Более формально барабан рассматривается как эластичная мембрана, граница которой зажата. Он представлен в виде области D на плоскости . Обозначим через λ _n собственные значения Дирихле для D : то есть собственные значения задачи Дирихле для лапласиана :

{\begin{cases}\Delta u+\lambda u=0\\u|_{\partial D}=0\end{cases}}

Две области называются изоспектральными (или гомофонными), если они имеют одинаковые собственные значения. Термин «гомофонический» оправдан, поскольку собственные значения Дирихле являются именно теми фундаментальными тонами, которые способен воспроизводить барабан: они естественным образом появляются как коэффициенты Фурье в решении волнового уравнения с зажатой границей.

Поэтому вопрос можно переформулировать так: что можно сделать вывод о D , если известны только значения λ _n ? Или, более конкретно: существуют ли две отдельные изоспектральные области?

Связанные проблемы могут быть сформулированы для задачи Дирихле для лапласиана в областях более высоких размерностей или на римановых многообразиях , а также для других эллиптических дифференциальных операторов , таких как оператор Коши-Римана или оператор Дирака . Помимо условия Дирихле, другие граничные условия, такие как граничное условие Неймана могут быть наложены и . См. Спектральную геометрию и изоспектральную информацию в соответствующих статьях.

Ответ [ править ]

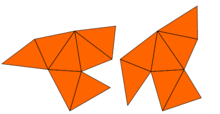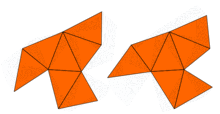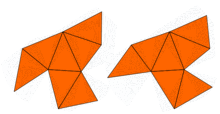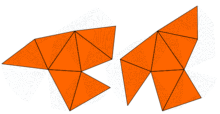
Однопараметрическое семейство изоспектральных барабанов

В 1964 году Джон Милнор заметил, что теорема Эрнста Витта о решетках предполагает существование пары 16-мерных плоских торов, имеющих одинаковые собственные значения, но разную форму. Однако проблема в двух измерениях оставалась открытой до 1992 года, когда Кэролин Гордон , Дэвид Уэбб и Скотт Вулперт построили на основе метода Сунады пару областей на плоскости, имеющих разную форму, но одинаковые собственные значения. Регионы представляют собой вогнутые многоугольники . Доказательство того, что обе области имеют одинаковые собственные значения, использует симметрии лапласиана. Эту идею обобщили Бузер, Конвей, Дойл и Земмлер. ^[4]который построил множество подобных примеров. услышать форму барабана Итак, ответ на вопрос Каца таков: для многих форм нельзя полностью . Однако некоторую информацию можно получить.

С другой стороны, Стив Зельдич доказал, что ответ на вопрос Каца будет положительным, если наложить ограничения на определенные выпуклые плоские области с аналитической границей. Неизвестно, могут ли две невыпуклые аналитические области иметь одинаковые собственные значения. Известно, что множество областей, изоспектральных данной, компактно в C ^∞топология. Более того, сфера (например) является спектрально жесткой по теореме Ченга о сравнении собственных значений . Благодаря результатам Осгуда, Филлипса и Сарнака известно также, что пространство модулей римановых поверхностей данного рода не допускает непрерывного изоспектрального потока через любую точку и компактно в топологии Фреше – Шварца.

Формула Вейля [ править ]

Формула Вейля гласит, что можно определить площадь A барабана, посчитав, насколько быстро растет λ _n . Мы определяем N ( R ) как количество собственных значений, меньших, чем R , и получаем

A=\omega _{d}^{-1}(2\pi )^{d}\lim _{R\to \infty }{\frac {N(R)}{R^{d/2}}},

где d - размерность, а $\omega _{d}$ — объем d -мерного единичного шара. Вейль также предположил, что следующий член в приведенном ниже приближении даст периметр D . Другими словами, если L обозначает длину периметра (или площадь поверхности в более высоком измерении), то следует иметь

N(R)=(2\pi )^{-d}\omega _{d}AR^{d/2}\mp {\frac {1}{4}}(2\pi )^{-d+1}\omega _{d-1}LR^{(d-1)/2}+o(R^{(d-1)/2}).

Для гладкой границы это было доказано Виктором Иврием в 1980 году. В многообразии также не допускается наличие двухпараметрического семейства периодических геодезических, как у сферы.

Вейля Гипотеза Берри -

предположил , что для негладких границ В 1979 году Майкл Берри поправка должна быть порядка

R^{D/2},

где D — хаусдорфова размерность границы. Это было опровергнуто Ж. Броссаром и Р. А. Кармоной, которые затем предложили заменить размерность Хаусдорфа на размерность верхнего ящика . На плоскости это было доказано, если граница имеет размерность 1 (1993 г.), но в основном опровергнуто для более высоких измерений (1996 г.); оба результата принадлежат Лапидусу и Померансу .

См. также [ править ]

Примечания [ править ]

^ Кроуэлл, Рэйчел (28 июня 2022 г.), «Математики пытаются «услышать» формы — и достичь более высоких измерений» , Scientific American , получено 15 ноября 2022 г.
^ «Можно ли услышать форму барабана? | Математическая ассоциация Америки»
^ Кац, Марк (апрель 1966 г.), «Можно ли услышать форму барабана?» (PDF) , American Mathematical Monthly , 73 (4, часть 2): 16, doi : 10.2307/2313748 , JSTOR 2313748
^ Бузер и др. 1994 .

Ссылки [ править ]

Абикофф, Уильям (январь 1995 г.), «Вспоминая Липмана Берса» (PDF) , Уведомления AMS , 42 (1): 8–18.
Броссар, Жан; Кармона, Рене (1986), «Можно ли услышать размерность фрактала?» , Комм. Математика. Физ. , 104 (1): 103–122, Bibcode : 1986CMaPh.104..103B , doi : 10.1007/BF01210795 , S2CID 121173871
Бузер, Питер ; Конвей, Джон ; Дойл, Питер; Земмлер, Клаус-Дитер (1994), «Некоторые плоские изоспектральные области», International Mathematics Research Sciences , 1994 (9): 391–400, doi : 10.1155/S1073792894000437
Чепмен, С.Дж. (1995), «Барабаны, которые звучат одинаково», American Mathematical Monthly , 102 (февраль): 124–138, doi : 10.2307/2975346 , JSTOR 2975346
Жиро, Оливье; Тас, Коэн (2010), «Слуховые формы барабанов – математические и физические аспекты изоспектральности», Reviews of Modern Physics , 82 (3): 2213–2255, arXiv : 1101.1239 , Bibcode : 2010RvMP...82.2213G , doi : 10.1103/RevModPhys.82.2213 , S2CID 119289493
Гордон, Кэролайн ; Уэбб, Дэвид (1996), «Вы не можете услышать форму барабана», American Scientist , 84 (январь – февраль): 46–55, Бибкод : 1996AmSci..84...46G
Гордон, К .; Уэбб, Д .; Вулперт, С. (1992), «Изоспектральные плоские области и поверхности через римановы орбифолды», Inventiones Mathematicae , 110 (1): 1–22, Bibcode : 1992InMat.110....1G , doi : 10.1007/BF01231320 , S2CID 122258115
Иврий, В.Я. (1980), "Второй член спектральной асимптотики оператора Лапласа–Бельтрами на многообразиях с краем", Функц. Анальный. И Приложен , 14 (2): 25–34, doi : 10.1007/BF01086550 , S2CID 123935462 (на русском языке ).
Кац, Марк (апрель 1966 г.), «Можно ли услышать форму барабана?» (PDF) , American Mathematical Monthly , 73 (4, часть 2): 1–23, doi : 10.2307/2313748 , JSTOR 2313748
Лапидус, Мишель Л. (1991), «Можно ли услышать форму фрактального барабана? Частичное разрешение гипотезы Вейля-Берри», Геометрический анализ и компьютерная графика , Математика. наук. Рез. Инст. Опубл., т. 1, с. 17, Нью-Йорк: Springer, стр. 119–126, номер документа : 10.1007/978-1-4613-9711-3_13 , ISBN. 978-1-4613-9713-7
Лапидус, Мишель Л. (1993), «Вибрации фрактальных барабанов, гипотеза Римана , волны во фрактальных средах и гипотеза Вейля-Берри», в Б. Д. Слимане; Р. Дж. Джарвис (ред.), Обыкновенные дифференциальные уравнения и уравнения в частных производных, Том IV, Proc. Двенадцатый Интернат. Конф. (Данди, Шотландия, Великобритания, июнь 1992 г.) , Исследовательские заметки Питмана по математике. Серия, том. 289, Лондон: Longman and Технический, стр. 126–209.
Лапидус, МЛ; ван Франкенхейсен, М. (2000), Фрактальная геометрия и теория чисел: комплексные размерности фрактальных струн и нулей дзета-функций , Бостон: Биркхаузер . (Пересмотренное и дополненное второе издание выйдет в свет в 2005 г.)
Лапидус, Мишель Л.; Померанс, Карл (1993), «Дзета-функция Римана и одномерная гипотеза Вейля-Берри для фрактальных барабанов» , Proc. Лондонская математика. Соц. , Серия 3, 66 (1): 41–69, CiteSeerX 10.1.1.526.854 , doi : 10.1112/plms/s3-66.1.41
Лапидус, Мишель Л.; Померанс, Карл (1996), «Контрпримеры модифицированной гипотезе Вейля-Берри о фрактальных барабанах», Math. Учеб. Кембриджская философия. Соц. , 119 (1): 167–178, Bibcode : 1996MPCPS.119..167L , doi : 10.1017/S0305004100074053 , S2CID 33567484
Милнор, Джон (1964), «Собственные значения оператора Лапласа на некоторых многообразиях», Proceedings of the National Academy of Sciences of the United States of America , 51 (4): 542ff, Bibcode : 1964PNAS...51..542M , doi : 10.1073/pnas.51.4.542 , PMC 300113 , PMID 16591156
Сунада, Т. (1985), "Римановы накрытия и изоспектральные многообразия", Ann. математики. , 2, 121 (1): 169–186, номер документа : 10.2307/1971195 , JSTOR 1971195.
Зельдич, С. (2000), «Спектральное определение аналитических двуосесимметричных плоских областей», Геометрический и функциональный анализ , 10 (3): 628–677, arXiv : math/9901005 , doi : 10.1007/PL00001633 , S2CID 16324240

Внешние ссылки [ править ]

Моделирование , показывающее решения волнового уравнения в двух изоспектральных барабанах
Изоспектральные барабаны Тоби Дрисколла из Университета Делавэра
Некоторые плоские изоспектральные области Питера Бузера, Джона Хортона Конвея , Питера Дойла и Клауса-Дитера Земмлера
- 3D-рендеринг гомофонных барабанов Бузера-Конвея-Дойла-Семмлера
Барабаны, которые звучат одинаково, Иварс Петерсон на веб-сайте Математической ассоциации Америки
Вайсштейн, Эрик В. , «Изоспектральные многообразия» , MathWorld
Бенгурия, Рафаэль Д. (2001) [1994], «Собственное значение Дирихле» , Энциклопедия математики , EMS Press

[Crowell_SciAm_2022-1] Кроуэлл, Рэйчел (28 июня 2022 г.), «Математики пытаются «услышать» формы — и достичь более высоких измерений» , Scientific American , получено 15 ноября 2022 г.

[2] «Можно ли услышать форму барабана? | Математическая ассоциация Америки»

[3] Кац, Марк (апрель 1966 г.), «Можно ли услышать форму барабана?» (PDF) , American Mathematical Monthly , 73 (4, часть 2): 16, doi : 10.2307/2313748 , JSTOR 2313748

[FOOTNOTEBuserConwayDoyleSemmler1994-4] Бузер и др. 1994 .

[1]

[2]

[3]

[4]