Заказ-5 куб.сот

Заказ-5 куб.сот
Модели дисков Пуанкаре
Тип	Гиперболические обычные соты Равномерные гиперболические соты
Символ Шлефли	${4,3,5}$
Диаграмма Кокстера
Клетки	${4,3}$ ( куб )
Лица	${4}$ ( квадрат )
Краевая фигура	${5}$ ( пятиугольник )
Вершинная фигура	икосаэдр
Группа Коксетера	$ЧД 3, [4,3,5]$
Двойной	Додекаэдрические соты порядка 4
Характеристики	Обычный

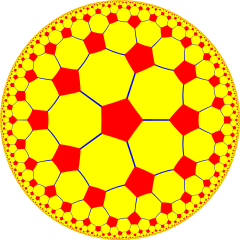
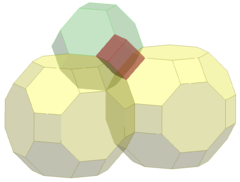
В гиперболической геометрии кубические соты пятого порядка — это одна из четырёх компактных регулярных , заполняющих пространство мозаик (или сот ) в гиперболическом трёхмерном пространстве . Символ Шлефли ${4,3,5}$ имеет пять кубов ${4,3}$ вокруг каждого ребра и 20 кубов вокруг каждой вершины . Он двойственен порядка додекаэдрическим сотам четвертого .

Геометрические соты — это заполнение пространства многогранными ячейками более высокой размерности или ячейками , чтобы не было пробелов. Это пример более общего математического разбиения или мозаики в любом количестве измерений.

Соты обычно строятся в обычном евклидовом («плоском») пространстве, как и выпуклые однородные соты . Они также могут быть построены в неевклидовых пространствах , таких как гиперболические однородные соты . Любой конечный однородный многогранник можно спроецировать на его описанную сферу, чтобы сформировать однородную соту в сферическом пространстве.

Описание

Это аналогично двумерной гиперболической квадратной мозаике пятого порядка , {4,5}

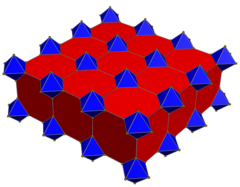
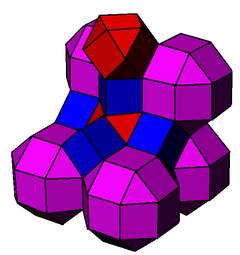
Одна ячейка с центром в модели шара Пуанкаре.	Основные ячейки	Ячейки с расширенными краями до идеальной границы

Симметрия

Он имеет конструкцию симметрии радикальной подгруппы с додекаэдрическими фундаментальными областями: обозначение Кокстера : [4,(3,5) ^*], индекс 120.

Связанные многогранники и соты

Кубические соты пятого порядка имеют родственные чередующиеся соты: ↔ , с икосаэдра и тетраэдра ячейками .

Соты также являются одной из четырех обычных компактных сот в трехмерном гиперболическом пространстве:

Четыре регулярных компактных сот в формате H ³
{5,3,4}	{4,3,5}	{3,5,3}	{5,3,5}

имеется пятнадцать однородных сот [5,3,4] В семействе групп Кокстера , включая кубические соты 5-го порядка как правильную форму:

[5,3,4] семейные соты
{5,3,4}	г {5,3,4}	т{5,3,4}	рр{5,3,4}	т _0,3 {5,3,4}	тр{5,3,4}	т _0,1,3 {5,3,4}	т _0,1,2,3 {5,3,4}


{4,3,5}	г {4,3,5}	т{4,3,5}	рр{4,3,5}	2т{4,3,5}	тр{4,3,5}	т _0,1,3 {4,3,5}	т _0,1,2,3 {4,3,5}

Кубические соты пятого порядка представляют собой последовательность правильных полихор и сот с икосаэдрическими вершинными фигурами .

{p,3,5} многогранники
Space	S³	H³
Form	Finite	Compact		Paracompact	Noncompact
Name	{3,3,5}	{4,3,5}	{5,3,5}	{6,3,5}	{7,3,5}	{8,3,5}	... {∞,3,5}
Image
Cells	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

Он также находится в последовательности правильных полихор и сот с кубическими ячейками . Первый многогранник в последовательности — это тессеракт , а второй — евклидовы кубические соты .

{4,3,p} обычные соты
Space	S³	E³	H³
Form	Finite	Affine	Compact	Paracompact	Noncompact
Name	{4,3,3}	{4,3,4}	{4,3,5}	{4,3,6}	{4,3,7}	{4,3,8}	... {4,3,∞}
Image
Vertex figure	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

Сот ректифицированный порядка 5 куб.

Сот ректифицированный порядка 5 куб.
Тип	Однородные соты в гиперболическом пространстве
Символ Шлефли	г{4,3,5} или 2р{5,3,4} 2р{5,3 ^1,1}
Диаграмма Кокстера	↔
Клетки	г{4,3} {3,5}
Лица	треугольник {3} квадрат {4}
Вершинная фигура	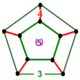пятиугольная призма
Группа Коксетера	${\overline {BH}}_{3}$ , [4,3,5] ${\overline {DH}}_{3}$ , [5,3 ^1,1]
Характеристики	Вершинно-транзитивный, реберно-транзитивный

Сот ректифицированный порядка 5 кубов , , имеет чередующиеся ячейки икосаэдра и кубооктаэдра , с пятиугольной призмы фигурой вершины .

Связанные соты

Его можно рассматривать как аналог двумерной гиперболической тетрапентагональной мозаики r{4,5} с квадратными и пятиугольными гранями.

Существует четыре выпрямленных компактных правильных сот:

Четыре выпрямленные регулярные компактные соты в H ³
Изображение
Символы	г {5,3,4}	г {4,3,5}	г {3,5,3}	г {5,3,5}
Вертекс фигура

г{р,3,5}
Космос	С ³	ЧАС ³
Форма	Конечный	Компактный		Паракомпакт	Некомпактный
Имя	г {3,3,5}	г {4,3,5}	г {5,3,5}	г {6,3,5}	г {7,3,5}	... г{∞,3,5}
Изображение
Клетки {3,5}	г{3,3}	г{4,3}	г{5,3}	г{6,3}	г{7,3}	г{∞,3}

Усеченные соты порядка 5 куб.

Усеченные соты порядка 5 куб.
Тип	Однородные соты в гиперболическом пространстве
Символ Шлефли	т{4,3,5}
Диаграмма Кокстера
Клетки	т{4,3} {3,5}
Лица	треугольник {3} восьмиугольник {8}
Вершинная фигура	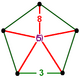пятиугольная пирамида
Группа Коксетера	${\overline {BH}}_{3}$ , [4,3,5]
Характеристики	Вершинно-транзитивный

Усеченные соты порядка 5 кубов , , имеет усеченные ячейки куба и икосаэдра , с пятиугольной пирамиды фигурой вершины .

Его можно рассматривать как аналог двумерной гиперболической усеченной квадратной мозаики пятого порядка , t{4,5}, с усеченным квадратом и пятиугольными гранями:

Он похож на евклидову усеченную кубическую соту (порядка 4) , t{4,3,4}, которая имеет октаэдрические ячейки в усеченных вершинах.

Связанные соты

Четыре усеченных правильных компактных сот в форме H. ³
Изображение
Символы	т{5,3,4}	т{4,3,5}	т{3,5,3}	т{5,3,5}
Вертекс фигура

Усеченные соты порядка 5 куб.

Кубические соты 5-го порядка с усеченными битами аналогичны додекаэдральным сотам 4-го порядка с битовыми усечками .

Смещенные соты порядка 5 куб.

Смещенные соты порядка 5 куб.
Тип	Однородные соты в гиперболическом пространстве
Символ Шлефли	рр{4,3,5}
Диаграмма Кокстера
Клетки	рр{4,3} г{3,5} {}х{5}
Лица	треугольник {3} квадрат {4} пятиугольник {5}
Вершинная фигура	клин
Группа Коксетера	${\overline {BH}}_{3}$ , [4,3,5]
Характеристики	Вершинно-транзитивный

Зубчатые соты порядка 5 куб ., , имеет ромбокубооктаэдр , икосододекаэдр и ячейки пятиугольной призмы с клиновидной вершиной .

Связанные соты

Он похож на евклидовы (четвертого порядка) зубчатые кубические соты , rr{4,3,4}:

Четыре зубчатых регулярных компактных сот в форме H. ³

Изображение
Символы	рр{5,3,4}	рр{4,3,5}	рр{3,5,3}	рр{5,3,5}
Вертекс фигура

Спиралевидные соты порядка 5 куб.

Спиралевидные соты порядка 5 куб.
Тип	Однородные соты в гиперболическом пространстве
Символ Шлефли	тр{4,3,5}
Диаграмма Кокстера
Клетки	тр{4,3} т{3,5} {}х{5}
Лица	квадрат {4} пятиугольник {5} шестигранник {6} восьмиугольник {8}
Вершинная фигура	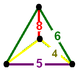зеркальная клиновидная кость
Группа Коксетера	${\overline {BH}}_{3}$ , [4,3,5]
Характеристики	Вершинно-транзитивный

Конусные соты порядка 5 кубических , , имеет усеченный кубооктаэдр , усеченный икосаэдр и ячейки пятиугольной призмы с зеркальной фигурой клиновидной вершины .

Связанные соты

Он похож на евклидову (порядка 4) изогнутую кубическую соту tr{4,3,4}:

Четыре скошенных регулярных компактных сот в форме H. ³
Изображение
Символы	тр{5,3,4}	тр{4,3,5}	тр{3,5,3}	тр{5,3,5}
Вертекс фигура

Соты проточенные порядка 5 куб.

Соты проточенные порядка 5 куб.
Тип	Однородные соты в гиперболическом пространстве Полурегулярные соты
Символ Шлефли	т _0,3 {4.3.5}
Диаграмма Кокстера
Клетки	{4,3} {5,3} {}х{5}
Лица	квадрат {4} пятиугольник {5}
Вершинная фигура	неправильная треугольная антипризма
Группа Коксетера	${\overline {BH}}_{3}$ , [4,3,5]
Характеристики	Вершинно-транзитивный

Сморщенные кубические соты 5-го порядка или сморщенные додекаэдрические соты 4-го порядка. , имеет куб , додекаэдр и пятиугольные призменные ячейки с неправильной треугольной вершиной антипризмы .

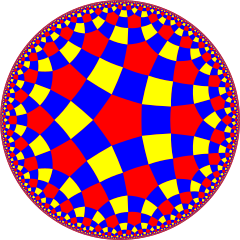
Это аналогично двумерной гиперболической ромбитетрапентагональной мозаике , rr{4,5}, с квадратными и пятиугольными гранями:

Связанные соты

Он аналогичен евклидовым (порядка 4) сморщенным кубическим сотам , t _0,3 {4,3,4}:

Три сучковатых правильных компактных сот в форме H. ³
Изображение
Символы	т _0,3 {4.3.5}	т _0,3 {3,5,3}	т _0,3 {5,3,5}
Вертекс фигура

Сотовый кубический усеченный порядка 5 куб.

Усеченные соты порядка 5 куб. Додекаэдрические соты Runcicantellated порядка 4
Тип	Однородные соты в гиперболическом пространстве
Символ Шлефли	т _0,1,3 {4,3,5}
Диаграмма Кокстера
Клетки	т{4,3} рр{5,3} {}х{5} {}x{8}
Лица	треугольник {3} квадрат {4} пятиугольник {5} восьмиугольник {8}
Вершинная фигура	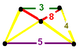равнобедренно-трапециевидная пирамида
Группа Коксетера	${\overline {BH}}_{3}$ , [4,3,5]
Характеристики	Вершинно-транзитивный

или Кубические соты 5-го порядка додекаэдрические соты 4-го порядка , , имеет усеченный куб , ромбокосододекаэдр , пятиугольную призму и ячейки восьмиугольной призмы , с равнобедренно-трапециевидной пирамиды фигурой вершины .

Связанные соты

Он похож на евклидовы (порядка 4) усеченные кубические соты , t _0,1,3 {4,3,4}:

Четыре правильных компактных сот с усеченными краями в форме H. ³

Ранциконтеллярные соты кубического порядка 5

Кубические соты 5-го порядка с продолговатыми усеченными элементами аналогичны додекаэдральным сотам 4-го порядка со скругленными усеченными элементами .

Всеусеченные соты порядка 5 куб.

Всеусеченные соты порядка 5 куб.
Тип	Однородные соты в гиперболическом пространстве Полурегулярные соты
Символ Шлефли	т _0,1,2,3 {4,3,5}
Диаграмма Кокстера
Клетки	тр{5,3} тр{4,3} {10}х{} {8}х{}
Лица	квадрат {4} шестигранник {6} восьмиугольник {8} десятиугольник {10}
Вершинная фигура	неправильный тетраэдр
Группа Коксетера	${\overline {BH}}_{3}$ , [4,3,5]
Характеристики	Вершинно-транзитивный

Всеусеченные кубические соты 5-го порядка или всеусеченные додекаэдрические соты 4-го порядка , , имеет усеченный икосододекаэдр , усеченный кубооктаэдр , десятиугольную призму и ячейки восьмиугольной призмы с неправильной тетраэдрической вершинной фигурой.

Связанные соты

Он похож на евклидову (порядка 4) всеусеченные кубические соты , t _0,1,2,3 {4,3,4}:

Три всеусеченных правильных компактных сот в форме H. ³

Попеременный порядок - 5-кубовые соты

Попеременный порядок - 5-кубовые соты
Тип	Однородные соты в гиперболическом пространстве
Символ Шлефли	ч{4,3,5}
Диаграмма Кокстера	↔
Клетки	{3,3} {3,5}
Лица	треугольник {3}
Вершинная фигура	икосододекаэдр
Группа Коксетера	${\overline {DH}}_{3}$ , [5,3 ^1,1]
Характеристики	Вершинно-транзитивный, реберно-транзитивный, квазирегулярный

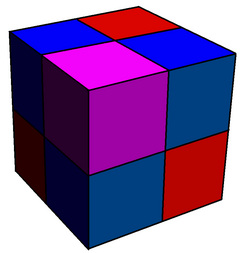
В трехмерной гиперболической геометрии чередующиеся кубические соты пятого порядка представляют собой однородную компактную мозаику , заполняющую пространство (или соты ). С символом Шлефли h{4,3,5} его можно рассматривать как квазиправильные соты , в которых чередуются икосаэдры и тетраэдры вокруг каждой вершины в вершинной фигуре икосододекаэдра .

Связанные соты

Имеет 3 родственные формы: кантический порядок — 5 кубических сот , , рунический порядок - 5-кубовые соты , , и рунические соты порядка 5 кубических , .

Кантический порядок-5 куб.сот

Кантический порядок-5 куб.сот
Тип	Однородные соты в гиперболическом пространстве
Символ Шлефли	ч ₂ {4,3,5}
Диаграмма Кокстера	↔
Клетки	г{5,3} т{3,5} т{3,3}
Лица	треугольник {3} пятиугольник {5} шестигранник {6}
Вершинная фигура	прямоугольная пирамида
Группа Коксетера	${\overline {DH}}_{3}$ , [5,3 ^1,1]
Характеристики	Вершинно-транзитивный

Кубические соты кантического порядка 5 представляют собой однородную компактную мозаику , заполняющую пространство (или соты ), с символом Шлефли h ₂ {4,3,5}. Он имеет икосододекаэдр , усеченный икосаэдр и усеченные ячейки тетраэдра с прямоугольной пирамиды вершиной .

Руничник порядка 5 куб.сот

Руничник порядка 5 куб.сот
Тип	Однородные соты в гиперболическом пространстве
Символ Шлефли	ч ₃ {4,3,5}
Диаграмма Кокстера	↔
Клетки	{5,3} рр{5,3} {3,3}
Лица	треугольник {3} квадрат {4} пятиугольник {5}
Вершинная фигура	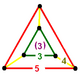треугольная деталь
Группа Коксетера	${\overline {DH}}_{3}$ , [5,3 ^1,1]
Характеристики	Вершинно-транзитивный

Кубические соты рунического порядка 5 представляют собой однородную компактную мозаику , заполняющую пространство (или соты ), с символом Шлефли h ₃ {4,3,5}. Он состоит из додекаэдра , ромбикосидодекаэдра и тетраэдра с усеченной треугольной вершиной .

Рансикантический порядок-5 кубических сот

Рансикантический порядок-5 кубических сот
Тип	Однородные соты в гиперболическом пространстве
Символ Шлефли	ч _2,3 {4,3,5}
Диаграмма Кокстера	↔
Клетки	т{5,3} тр{5,3} т{3,3}
Лица	треугольник {3} квадрат {4} шестигранник {6} десятиугольник {10}
Вершинная фигура	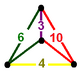неправильный тетраэдр
Группа Коксетера	${\overline {DH}}_{3}$ , [5,3 ^1,1]
Характеристики	Вершинно-транзитивный

Кубические соты рунцикантического порядка 5 представляют собой однородную компактную мозаику , заполняющую пространство (или соты ), с символом Шлефли h _2,3 {4,3,5}. Он имеет усеченный додекаэдр , усеченный икосододекаэдр и усеченные ячейки тетраэдра с неправильной тетраэдра фигурой вершины .

См. также

Ссылки

Коксетер , Правильные многогранники , 3-е. изд., Dover Publications, 1973. ISBN 0-486-61480-8 . (Таблицы I и II: Правильные многогранники и соты, стр. 294–296)
Коксетер , Красота геометрии: двенадцать эссе , Dover Publications, 1999 г. ISBN 0-486-40919-8 (Глава 10: Правильные соты в гиперболическом пространстве, Сводные таблицы II, III, IV, V, стр. 212-213)
Нормана Джонсона Равномерные многогранники , рукопись
- Н. В. Джонсон : Теория однородных многогранников и сот , доктор философии. Диссертация, Университет Торонто, 1966 г.
- Н. В. Джонсон: Геометрии и преобразования , (2015) Глава 13: Гиперболические группы Кокстера