Функция Эйлера

В чисел теории функция тотента Эйлера подсчитывает положительные целые числа до заданного целого числа n, которые являются относительно простыми с n . Оно пишется греческой буквой фи как или , а также может быть названа фи-функцией Эйлера . Другими словами, это количество целых чисел k в диапазоне 1 ≤ k ≤ n , для которых наибольший общий делитель НОД( n , k ) равен 1. [2] [3] Целые числа k этой формы иногда называют совокупными n числами .
Например, совокупные числа n = 9 — это шесть чисел 1, 2, 4, 5, 7 и 8. Все они взаимно просты с 9, но остальные три числа в этом диапазоне — 3, 6 и 9 — нет. , поскольку gcd(9, 3) = gcd(9, 6) = 3 и gcd(9, 9) = 9 . Следовательно, φ (9) = 6 . Другой пример: φ (1) = 1 , поскольку при n = 1 единственное целое число в диапазоне от 1 до n равно 1, а gcd(1, 1) = 1 .
Функция тотента Эйлера является мультипликативной функцией , что означает, что если два числа m и n взаимно простые, то φ ( mn ) = φ ( m ) φ ( n ) . [4] [5] Эта функция задаёт мультипликативной группы целых чисел по n ( группы единиц модулю кольца порядок ). [6] Он также используется для определения системы шифрования RSA .
История, терминология и обозначения
[ редактировать ]Леонард Эйлер ввел эту функцию в 1763 году. [7] [8] [9] Однако в то время он не выбрал для его обозначения какого-либо конкретного символа. В публикации 1784 года Эйлер изучил функцию дальше, выбрав для ее обозначения греческую букву π : он написал πD для «множества чисел, меньших D и не имеющих с ним общего делителя». [10] Это определение отличается от текущего определения функции тотента при D = 1, но в остальном остается тем же. Теперь стандартные обозначения [8] [11] φ ( A ) взято из трактата Гаусса 1801 года «Арифметические исследования» : [12] [13] хотя Гаусс не стал заключать аргумент в круглые скобки и написал φA . Поэтому ее часто называют фи-функцией Эйлера или просто фи-функцией .
В 1879 году Дж. Дж. Сильвестр термин totient : ввел для этой функции [14] [15] поэтому ее также называют функцией Эйлера , функцией Эйлера или функцией Эйлера . Тотент Джордана является обобщением Эйлера.
Кофактор n n определяется ( - φ ) n . как Он подсчитывает количество натуральных чисел, меньших или равных n , которые имеют хотя бы один простой делитель общий с n .
Вычисление функции Эйлера
[ редактировать ]Существует несколько формул для вычисления φ ( n ) .
Формула произведения Эйлера
[ редактировать ]В нем говорится
где произведение находится на различных простых числах, делящих n . (Обозначения см. в разделе «Арифметическая функция ».)
Эквивалентная формулировка где является основной факторизацией (то есть, являются различными простыми числами).
Доказательство этих формул зависит от двух важных фактов.
Фи — мультипликативная функция
[ редактировать ]Это означает, что если НОД( m , n ) = 1 , то φ ( m ) φ ( n ) = φ ( mn ) . Схема доказательства: Пусть A , B , C — множества натуральных чисел, которые взаимно просты и меньше m , n , mn соответственно, так что | А | = φ ( m ) и т. д. Тогда существует взаимно однозначное соответствие между A × B и C согласно китайской теореме об остатках .
Значение фи для аргумента простой степени
[ редактировать ]Если p простое число и k ≥ 1 , то
Доказательство . Поскольку p — простое число, единственные возможные значения gcd( p к , m ) равны 1, p , p 2 , ..., п к и единственный способ получить gcd( p к , m ) > 1 , если m кратно p , то есть m ∈ { p , 2 p , 3 p , ..., p к - 1 р = р к } , и есть p к - 1 такие кратные не превосходят p к . Следовательно, другой п к − п к - 1 все числа относительно просты с p к .
Доказательство формулы произведения Эйлера
[ редактировать ]Основная теорема арифметики гласит, что если n > 1, существует единственное выражение где p 1 < p 2 < ... < p r — простые числа и каждое k i ≥ 1 . (Случай n = 1 соответствует пустому произведению.) Многократно используя мультипликативное свойство φ и формулу для φ ( p к ) дает
Это дает обе версии формулы произведения Эйлера.
Альтернативное доказательство, которое не требует мультипликативного свойства, вместо этого использует принцип включения-исключения, применяемый к множеству. , исключая наборы целых чисел, делящихся на простые делители.
Пример
[ редактировать ]Другими словами: отдельные простые делители числа 20 — это 2 и 5; половина из двадцати целых чисел от 1 до 20 делится на 2, остается десять; пятая часть из них делится на 5, в результате чего восемь чисел взаимно просты с 20; это: 1, 3, 7, 9, 11, 13, 17, 19.
Альтернативная формула использует только целые числа:
Преобразование Фурье
[ редактировать ]Тотент — это преобразование Фурье НОД дискретное , оцененное как 1. [16] Позволять
где x k = НОД( k , n ) для k ∈ {1, ..., n } . Затем
Действительная часть этой формулы
Например, используя и : В отличие от произведения Эйлера и формулы суммы делителей, здесь не требуется знать множители n . Однако он включает в себя вычисление наибольшего общего делителя n и каждого положительного целого числа меньше n , чего в любом случае достаточно для факторизации.
Делитель суммы
[ редактировать ]Свойство, установленное Гауссом, [17] что
где сумма вычисляется по всем положительным делителям d числа n , можно доказать несколькими способами. (Условия обозначений см . в разделе «Арифметическая функция» .)
Одним из доказательств является то, что ( d ) также равно числу возможных образующих циклической группы Cd φ ; в частности, если C d = ⟨ g ⟩ с g д = 1 , то г к является генератором для каждого k, взаимно простого с d . Поскольку каждый элемент Cn Cn порождает циклическую подгруппу , а каждая подгруппа порождается . ровно φ ⊆ ( d ) элементами Cd , формула Cn следующая [18] Эквивалентно, формула может быть получена с помощью того же аргумента, который применяется к мультипликативной группе корней n- й степени из единицы и примитивных корней d -й степени из единицы .
Формулу также можно вывести из элементарной арифметики. [19] Например, пусть n = 20 и рассмотрим положительные дроби до 1 со знаменателем 20:
Изложите их в самых низких терминах:
Все эти двадцать дробей положительные. k / d ≤ 1, знаменателями которого являются делители d = 1, 2, 4, 5, 10, 20 . Дроби со знаменателем 20 – это дроби, числители которых относительно просты с 20, а именно: 1 / 20 , 3 / 20 , 7 / 20 , 9 / 20 , 11 / 20 , 13 / 20 , 17 / 20 , 19/20 ; по определению это φ (20) дроби. Точно так же существуют дроби φ (10) со знаменателем 10, дроби φ (5) со знаменателем 5 и т. д. Таким образом, набор из двадцати дробей разбивается на подмножества размера φ ( d ) для каждого d, делящего 20. Аналогичный аргумент применяется для любого n.
Обращение Мёбиуса, примененное к формуле суммы делителей, дает
где µ — функция Мёбиуса , мультипликативная функция , определяемая формулой и для каждого простого числа p и k ≥ 2 . Эту формулу также можно получить из формулы произведения путем умножения получить
Пример:
Некоторые значения
[ редактировать ]Первые 100 значений (последовательность A000010 в OEIS ) показаны в таблице и на графике ниже:
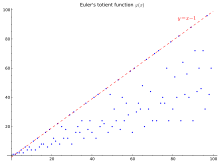
φ ( n ) для 1 ≤ n ≤ 100 + 1 2 3 4 5 6 7 8 9 10 0 1 1 2 2 4 2 6 4 6 4 10 10 4 12 6 8 8 16 6 18 8 20 12 10 22 8 20 12 18 12 28 8 30 30 16 20 16 24 12 36 18 24 16 40 40 12 42 20 24 22 46 16 42 20 50 32 24 52 18 40 24 36 28 58 16 60 60 30 36 32 48 20 66 32 44 24 70 70 24 72 36 40 36 60 24 78 32 80 54 40 82 24 64 42 56 40 88 24 90 72 44 60 46 72 32 96 42 60 40
На графике справа верхняя линия y = n − 1 представляет собой верхнюю границу , действительную для всех n, кроме единицы, и достигается тогда и только тогда, когда n — простое число. Простая нижняя граница , что довольно расплывчато: фактически нижняя граница графика пропорциональна п / журнал журнал п . [20]
Теорема Эйлера
[ редактировать ]Это означает, что если a и n , взаимно простые то
Особый случай, когда n — простое число, известен как малая теорема Ферма .
Это следует из теоремы Лагранжа и того факта, что φ ( n ) — это порядок мультипликативной группы целых чисел по модулю n .
Криптосистема RSA основана на этой теореме: из нее следует, что обратная функция a ↦ a и mod n , где e — (публичный) показатель шифрования, — это функция b ↦ b д mod n , где d , (частный) показатель дешифрования, является мультипликативным обратным по e модулю φ ( n ) . Таким образом, сложность вычисления φ ( n ) без знания факторизации n является трудностью вычисления d : это известно как проблема RSA , которую можно решить путем факторизации n . Владелец закрытого ключа знает факторизацию, поскольку закрытый ключ RSA создается путем выбора n как произведения двух (случайно выбранных) больших простых чисел p и q . только n Публично раскрыто , и, учитывая сложность факторизации больших чисел, у нас есть гарантия, что никто больше не знает факторизации.
Другие формулы
[ редактировать ]В частности:
Сравните это с формулой (см. наименьшее общее кратное ).
- φ ( n ) четно для n ≥ 3 .
Более того, если n имеет r различных нечетных простых делителей, 2 р | φ ( п )
- Для любых a > 1 и n > 6 таких, что 4 ∤ n, существует l ≥ 2 n такое, что l | φ ( а н − 1) .
где rad( n ) — радикал числа n (произведение всех различных простых чисел, делящих n ).
- [21]
- ( [22] цитируется в [23] )
- [Лю (2016)]
- [22]
- [24]
- [24]
(где γ — постоянная Эйлера–Машерони ).
Личность Менона
[ редактировать ]В 1965 году П. Кесава Менон доказал
где d ( n ) знак равно σ 0 ( n ) количество делителей n .
Делимость на любое фиксированное положительное целое число
[ редактировать ]Следующее свойство, являющееся частью «фольклора» (т.е., видимо, неопубликованное как конкретный результат: [25] см. введение к этой статье, в котором говорится, что оно «давно известно»), имеет важные последствия. Например, это исключает равномерное распределение значений в арифметических прогрессиях по модулю для любого целого числа .
- Для каждого фиксированного положительного целого числа , отношение подходит почти для всех , то есть для всех, кроме значения как .
Это элементарное следствие того факта, что сумма обратных простых чисел, совпадающих с 1 по модулю расходится, что само по себе является следствием доказательства теоремы Дирихле об арифметических прогрессиях .
Генерирующие функции
[ редактировать ]Ряд Дирихле для φ ( n ) можно записать через дзета-функцию Римана как: [26]
где левая часть сходится для .
ряда Ламберта : Производящая функция [27]
который сходится для | д | < 1 .
Оба они доказываются манипуляциями с элементарными рядами и формулами для φ ( n ) .
Темпы роста
[ редактировать ]По словам Харди и Райта, порядок φ ( n ) «всегда «почти n ». [28]
Первый [29]
но когда n стремится к бесконечности, [30] для всех δ > 0
Эти две формулы можно доказать, используя немного больше, чем формулы для φ ( n ) и функции суммы делителей σ ( n ) .
Действительно, при доказательстве второй формулы выполнено неравенство
верно для n > 1 , доказано.
У нас также есть [20]
Здесь γ — постоянная Эйлера , γ = 0,577215665... , поэтому e с = 1,7810724... и е − с = 0.56145948... .
Для доказательства этого не требуется теорема о простых числах . [31] [32] Поскольку log log n стремится к бесконечности, эта формула показывает, что
На самом деле, правда больше. [33] [34] [35]
и
Второе неравенство было показано Жаном-Луи Николя . Рибенбойм говорит: «Метод доказательства интересен тем, что неравенство сначала показывается в предположении, что гипотеза Римана верна, а во-вторых, в противоположном предположении». [35] : 173
Для среднего заказа у нас есть [22] [36]
принадлежит Арнольду Вальфису , доказательство с использованием оценок экспоненциальных сумм принадлежит И. М. Виноградову и Н. М. Коробову . Комбинируя методы Ван дер Корпута и Виноградова, Х.-К. Лю (О функции Эйлера. Proc. Roy. Soc. Edinburgh Sect. A 146 (2016), № 4, 769–775) улучшил термин ошибки до
(на данный момент это самая известная оценка такого типа). О «Большой » обозначает величину, которая ограничена константой, умноженной на функцию n внутри круглых скобок (которая мала по сравнению с n 2 ).
Этот результат можно использовать для доказательства [37] что вероятность того, что два случайно выбранных числа окажутся относительно простыми, равна 6 / п 2 .
Соотношение последовательных значений
[ редактировать ]В 1950 году Сомаяджулу доказал [38] [39]
В 1954 году Шинцель и Серпинский усилили это, доказав [38] [39] что набор
плотно . в положительных действительных числах Они также доказали [38] что набор
плотно в интервале (0,1).
Так много цифр
[ редактировать ]Тотентное число — это значение тотент-функции Эйлера: то есть m , для которого существует хотя бы одно n, для которого φ ( n ) = m . Валентность кратность или . общего числа m — это количество решений этого уравнения [40] число Нетоентное — натуральное число, не являющееся тотентным. Каждое нечетное целое число, превышающее 1, тривиально является нетотиентом. Есть также бесконечно много даже не-тотиентов, [41] и действительно, каждое положительное целое число имеет кратное число, которое является четным. [42]
Число тотентных чисел до заданного предела x равно
для константы C = 0,8178146... . [43]
Если считать в соответствии с кратностью, количество общих чисел до заданного предела x равно
где член ошибки R имеет порядок не более х / (логарифм х ) к для любого положительного k . [44]
Известно, что кратность m превышает m д бесконечно часто для любого δ < 0,55655 . [45] [46]
Теорема Форда
[ редактировать ]Форд (1999) доказал, что для каждого целого числа k ≥ 2 существует общее число m кратности k : то есть, для которого уравнение φ ( n ) = m имеет ровно k решений; этот результат ранее был предположен Вацлавом Серпинским , [47] и оно было получено как следствие гипотезы Шинцеля H . [43] Действительно, каждая возникающая множественность происходит бесконечно часто. [43] [46]
Однако число m с кратностью k = 1 неизвестно . Гипотеза Кармайкла о полной функции не существует — это утверждение, что такого m . [48]
Идеальные социальные числа
[ редактировать ]Совершенное числовое число — это целое число, равное сумме его повторяющихся частей. То есть мы применяем функцию totient к числу n , применяем ее снова к полученному totient и так далее, пока не будет достигнуто число 1, и складываем полученную последовательность чисел; если сумма равна n , то n — совершенное число.
Приложения
[ редактировать ]Циклопомия
[ редактировать ]В последнем разделе Disquisitiones [49] [50] Гаусс доказывает [51] что правильный n -угольник можно построить с помощью линейки и циркуля, если φ ( n ) является степенью 2. Если n является степенью нечетного простого числа, формула для тотента говорит, что его тотент может быть степенью двойки, только если n — первая степень, а n — 1 — степень 2. Простые числа, которые на единицу больше степени 2, называются простыми числами Ферма , и известны только пять: 3, 5, 17, 257 и 65537. Ферма и Гаусс знал об этом. Никто не смог доказать, есть ли еще.
Таким образом, правильный n -угольник имеет конструкцию «линейка и циркуль», если n является произведением различных простых чисел Ферма и любой степени двойки. Первые несколько таких n равны [52]
- 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40,... (последовательность A003401 в OEIS ).
Теорема о простых числах для арифметических прогрессий
[ редактировать ]Криптосистема RSA
[ редактировать ]Настройка системы RSA включает выбор больших простых чисел p и q , вычисление n = pq и k = φ ( n ) и поиск двух чисел e и d таких, что ed ≡ 1 (mod k ) . Числа n и e («ключ шифрования») публикуются, а d («ключ дешифрования») остается конфиденциальным.
Сообщение, представленное целым числом m , где 0 < m < n , шифруется путем вычисления S = m. и (против н ) .
Он расшифровывается путем вычисления t = S д (мод. н ) . Теорему Эйлера можно использовать, чтобы показать, что если 0 < t < n , то t = m .
Безопасность системы RSA была бы поставлена под угрозу, если бы число n можно было эффективно разложить на множители или если φ ( n ) можно было бы эффективно вычислить без факторизации n .
Нерешенные проблемы
[ редактировать ]Гипотеза Лемера
[ редактировать ]Если p простое число, то φ ( p ) = p − 1 . В 1932 году Д. Х. Лемер спросил, существуют ли составные числа n такие, что φ ( n ) делит n −1 . Ни один из них не известен. [53]
В 1933 году он доказал, что если такое n существует, то оно должно быть нечетным, свободным от квадратов и делиться как минимум на семь простых чисел (т.е. ω ( n ) ≥ 7 ). В 1980 году Коэн и Хагис доказали, что n > 10. 20 и что ω ( n ) ≥ 14 . [54] Далее Хагис показал, что если 3 делит n , то n > 10. 1937042 и ω ( n ) ≥ 298848 . [55] [56]
Гипотеза Кармайкла
[ редактировать ]Это означает, что не существует числа n, обладающего свойством, которое для всех остальных чисел m , m ≠ n , φ ( m ) ≠ φ ( n ) . См . теорему Форда выше.
Как сказано в основной статье, если существует единственный контрпример к этой гипотезе, то контрпримеров должно быть бесконечно много, и самый маленький из них имеет не менее десяти миллиардов цифр по основанию 10. [40]
Гипотеза Римана
[ редактировать ]Гипотеза Римана верна тогда и только тогда, когда выполнено неравенство
верно для всех n ≥ p 120569 # , где γ — константа Эйлера , а p 120569 # — произведение первых 120569 простых чисел. [57]
См. также
[ редактировать ]Примечания
[ редактировать ]- ^ «Тотентная функция Эйлера» . Ханская академия . Проверено 26 февраля 2016 г.
- ^ Лонг (1972 , стр. 85)
- ^ Петтофреззо и Биркит (1970 , стр. 72)
- ^ Лонг (1972 , стр. 162)
- ^ Петтофреззо и Биркит (1970 , стр. 80)
- ^ См . теорему Эйлера .
- ^ Л. Эйлер « Теоремата арифметика нова методо демонстрата » (Арифметическая теорема, доказанная новым методом), Novi commentarii academiae scientiarum Imperialis Petropolitanae (Новые мемуары Санкт-Петербургской Императорской Академии наук), 8 (1763), 74–104 . (Работа была представлена в Петербургской Академии 15 октября 1759 года. Одноименная работа была представлена в Берлинской Академии 8 июня 1758 года). Доступно в Интернете: Фердинанд Рудио , изд. , Leonhardi Euleri Commentationes Arithmeticae , том 1, в: Leonhardi Euleri Opera Omnia , серия 1, том 2 (Лейпциг, Германия, Б. Г. Тойбнер, 1915), страницы 531–555 . На странице 531 Эйлер определяет n как количество целых чисел, меньших N и взаимно простых с N (... aequalis sit multitudini numerorum ipso N minorum, qui simul ad eum sint primi, ...), что является фи функция φ(N).
- ↑ Перейти обратно: Перейти обратно: а б Сандифер, с. 203
- ^ Грэм и др. п. 133 примечание 111
- ^ Л. Эйлер, Рассуждения о некоторых примечательных свойствах чисел , Труды Императорской Академии наук Петрополитины, том. 4, (1784), с. 18–30, или Opera Omnia, серия 1, том 4, с. 105–115. (Работа была представлена в Петербургской Академии 9 октября 1775 г.).
- ^ И φ ( n ) , и φ ( n ) встречаются в литературе. Это две формы строчной греческой буквы фи .
- ^ Гаусс, Disquisitiones Arithmeticae, статья 38
- ^ Каджори, Флориан (1929). История математических обозначений, том II . Издательство «Открытый суд». §409.
- ^ Дж. Дж. Сильвестр (1879) «О некоторых троичных уравнениях кубической формы», Американский журнал математики , 2 : 357-393; Сильвестр вводит термин «тотиент» на странице 361 .
- ^ «тотиент». Оксфордский словарь английского языка (2-е изд.). Издательство Оксфордского университета . 1989.
- ^ Шрамм (2008)
- ^ Гаусс, Д.А., арт 39.
- ^ Гаусс, Д.А. ст. 39, ст. 52-54
- ^ Грэм и др. стр. 134-135
- ↑ Перейти обратно: Перейти обратно: а б Харди и Райт, 1979 , thm. 328
- ^ Динева (во внешних ссылках), подп. 1
- ↑ Перейти обратно: Перейти обратно: а б с Вальфиш, Арнольд (1963). Экспоненциальные суммы Вейля в современной теории чисел . Отчеты о математических исследованиях (на немецком языке). Том 16. Берлин: Немецкое научное издательство VEB . Збл 0146.06003 .
- ^ Г. (1964) Ломадсе , , , Acta Arithmetica 10 ( 3): 227–237, doi : 10.4064/aa-10-3-227-237
- ↑ Перейти обратно: Перейти обратно: а б Ситарамачандрарао, Р. (1985). «Об ошибочном термине Ландау II» . Роки Маунтин Дж. Математика . 15 (2): 579–588. дои : 10.1216/RMJ-1985-15-2-579 .
- ^ Поллак, П. (2023), «Две задачи о распределении лямбда-функции Кармайкла», Mathematika , 69 : 1195–1220, arXiv : 2303.14043 , doi : 10.1112/mtk.12222
- ^ Харди и Райт 1979 , thm. 288
- ^ Харди и Райт 1979 , thm. 309
- ^ Харди и Райт 1979 , введение к § 18.4.
- ^ Харди и Райт 1979 , thm. 326
- ^ Харди и Райт 1979 , thm. 327
- ^ Фактически теорема Чебышева ( Hardy & Wright 1979 , thm.7) иТретья теорема Мертенса — это все, что нужно.
- ^ Харди и Райт 1979 , thm. 436
- ^ Теорема 15 из Россер, Дж. Баркли; Шенфельд, Лоуэлл (1962). «Приближенные формулы для некоторых функций простых чисел» . Иллинойс Дж. Математика . 6 (1): 64–94. дои : 10.1215/ijm/1255631807 .
- ^ Бах и Шалит, thm. 8.8.7
- ↑ Перейти обратно: Перейти обратно: а б Рибенбойм (1989). «Как распределяются простые числа? §IC Распределение значений функции Эйлера». Книга рекордов простых чисел (2-е изд.). Нью-Йорк: Springer-Verlag. стр. 172–175. дои : 10.1007/978-1-4684-0507-1_5 . ISBN 978-1-4684-0509-5 .
- ^ Шандор, Митринович и Крстичи (2006), стр. 24–25.
- ^ Харди и Райт 1979 , thm. 332
- ↑ Перейти обратно: Перейти обратно: а б с Рибенбойм, стр.38
- ↑ Перейти обратно: Перейти обратно: а б Шандор, Митринович и Крстичи (2006), стр.16
- ↑ Перейти обратно: Перейти обратно: а б Гай (2004) стр.144
- ^ Шандор и Крстичи (2004) стр.230
- ^ Чжан, Минчжи (1993). «О нетентах» . Журнал теории чисел . 43 (2): 168–172. дои : 10.1006/jnth.1993.1014 . ISSN 0022-314X . Збл 0772.11001 .
- ↑ Перейти обратно: Перейти обратно: а б с Форд, Кевин (1998). «Распределение вещей». Рамануджан Дж . Развитие математики. 2 (1–2): 67–151. arXiv : 1104.3264 . дои : 10.1007/978-1-4757-4507-8_8 . ISBN 978-1-4419-5058-1 . ISSN 1382-4090 . Збл 0914.11053 .
- ^ Шандор и др. (2006) стр.22
- ^ Шандор и др. (2006) стр.21
- ↑ Перейти обратно: Перейти обратно: а б Гай (2004) стр.145
- ^ Шандор и Крстичи (2004) стр.229
- ^ Шандор и Крстичи (2004) стр.228
- ^ Гаусс, Д.А. 7-й § – искусство. 336–366
- ^ Гаусс доказал, что если n удовлетворяет определенным условиям, то n -угольник можно построить. В 1837 году Пьер Ванцель доказал обратное: если n -угольник конструктивен, то n должно удовлетворять условиям Гаусса.
- ^ Гаусс, Д.А., арт 366.
- ^ Гаусс Д.А., ст. 366. Этот список является последним предложением в « Рассуждениях».
- ^ Рибенбойм, стр. 36–37.
- ^ Коэн, Грэм Л.; Хагис, Питер младший (1980). «О количестве простых делителей числа n , если φ ( n ) делит n − 1 ». Нью-Арк. Вискд . III серия. 28 : 177–185. ISSN 0028-9825 . Збл 0436.10002 .
- ^ Хагис, Питер младший (1988). «Об уравнении M ·φ( n ) = n − 1 ». Нью-Арк. Вискд . IV серия. 6 (3): 255–261. ISSN 0028-9825 . Збл 0668.10006 .
- ^ Гай (2004) стр.142
- ^ Броган, Кевин (2017). Эквиваленты гипотезы Римана, Том первый: Арифметические эквиваленты (Первое изд.). Издательство Кембриджского университета. ISBN 978-1-107-19704-6 . Следствие 5.35.
Ссылки
[ редактировать ]Disquisitiones Arithmeticae переведена с латыни на английский и немецкий языки. Немецкое издание включает все статьи Гаусса по теории чисел: все доказательства квадратичной взаимности, определение знака суммы Гаусса, исследования биквадратной взаимности и неопубликованные заметки.
Ссылки на Disquisitiones имеют форму Gauss, DA, art. ннн .
- Абрамовиц, М .; Стегун, И.А. (1964), Справочник по математическим функциям , Нью-Йорк: Dover Publications , ISBN 0-486-61272-4 . См. параграф 24.3.2.
- Бах, Эрик ; Шалит, Джеффри (1996), Алгоритмическая теория чисел (Том I: Эффективные алгоритмы) , Серия MIT Press по основам вычислений, Кембридж, Массачусетс: MIT Press , ISBN 0-262-02405-5 , Збл 0873.11070
- Диксон, Леонард Юджин, «История теории чисел», том 1, глава 5 «Функция Эйлера, обобщения; ряд Фарея», Chelsea Publishing, 1952 г.
- Форд, Кевин (1999), «Число решений φ( x ) = m », Annals of Mathematics , 150 (1): 283–311, doi : 10.2307/121103 , ISSN 0003-486X , JSTOR 121103 , MR 1715326 , Збл 0978.11053 .
- Гаусс, Карл Фридрих (1986), Disquisitiones Arithmeticae (второе, исправленное издание) , перевод Кларка, Артура А., Нью-Йорк: Springer , ISBN 0-387-96254-9
- Гаусс, Карл Фридрих (1965), Исследования по высшей арифметике (второе издание) , перевод Мазера Х., Нью-Йорк: Челси, ISBN 0-8284-0191-8
- Грэм, Рональд ; Кнут, Дональд ; Паташник, Орен (1994), Конкретная математика : основа информатики (2-е изд.), Ридинг, Массачусетс: Аддисон-Уэсли, ISBN 0-201-55802-5 , Збл 0836.00001
- Гай, Ричард К. (2004), Нерешенные проблемы теории чисел , Сборники задач по математике (3-е изд.), Нью-Йорк, Нью-Йорк: Springer-Verlag , ISBN 0-387-20860-7 , Збл 1058.11001
- Харди, штат Джорджия ; Райт, Э.М. (1979), Введение в теорию чисел (пятое изд.), Оксфорд: Oxford University Press , ISBN 978-0-19-853171-5
- Лю, H.-Q. (2016), «О функции Эйлера», Тр. Рой. Соц. Эдинбургская секта. А , 146 (4) .
- Лонг, Кэлвин Т. (1972), Элементарное введение в теорию чисел (2-е изд.), Лексингтон: DC Heath and Company , LCCN 77-171950
- Петтофреззо, Энтони Дж.; Биркит, Дональд Р. (1970), Элементы теории чисел , Энглвуд Клиффс: Прентис Холл , LCCN 77-81766
- Рибенбойм, Пауло (1996), Новая книга рекордов простых чисел (3-е изд.), Нью-Йорк: Springer , ISBN 0-387-94457-5 , Збл 0856.11001
- Сандифер, Чарльз (2007), Ранняя математика Леонарда Эйлера , MAA, ISBN 978-0-88385-559-1
- Шандор, Джозеф; Митринович, Драгослав С.; Крстичи, Борислав, ред. (2006), Справочник по теории чисел I , Дордрехт: Springer-Verlag , стр. 9–36, ISBN 1-4020-4215-9 , Збл 1151.11300
- Шандор, Джозеф; Крстичи, Борислав (2004). Справочник по теории чисел II . Дордрехт: Клювер Академик. стр. 179 –327. ISBN 1-4020-2546-7 . Збл 1079.11001 .
- Шрамм, Вольфганг (2008), «Преобразование Фурье функций наибольшего общего делителя» , Электронный журнал комбинаторной теории чисел , A50 (8 (1)) .
Внешние ссылки
[ редактировать ]- «Тотиент-функция» , Математическая энциклопедия , EMS Press , 2001 [1994]
- Фи-функция Эйлера и китайская теорема об остатках - доказательство того, что φ ( n ) мультипликативна. Архивировано 28 февраля 2021 г. на Wayback Machine.
- Калькулятор функции Эйлера на JavaScript — до 20 цифр
- Динева, Розика, Тотент Эйлера, Мёбиуса и функции делителя. Архивировано 16 января 2021 г. в Wayback Machine.
- Плитейдж, Лумис, Полхилл суммируют фи-функцию Эйлера










![{\displaystyle {\begin{array}{rcl}\varphi (n)&=&\varphi (p_{1}^{k_{1}})\,\varphi (p_{2}^{k_{2} })\cdots \varphi (p_{r}^{k_{r}})\\[.1em]&=&p_{1}^{k_{1}}\left(1-{\frac {1}{ p_{1}}}\right)p_{2}^{k_{2}}\left(1- {\frac {1}{p_{2}}}\right)\cdots p_{r}^{k_ {r}}\left(1-{\frac {1}{p_{r}}}\right)\\[.1em]&=&p_{1}^{k_{1}}p_{2}^{ k_{2}}\cdots p_{r}^{k_{r}}\left(1-{\frac {1}{p_{1}}}\right)\left(1-{\frac {1} {p_{2}}}\right)\cdots \left(1-{\frac {1}{p_{r}}}\right)\\[.1em]&=&n\left(1-{\frac {1}{p_{1}}}\right)\left(1-{\frac {1}{p_{2}}}\right)\cdots \left(1-{\frac {1}{p_{ r}}}\right).\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7447918f84f4509322dda0b4aa4384ab8072a93)



![{\displaystyle {\mathcal {F}}\{\mathbf {x} \}[m]=\sum \limits _{k=1}^{n}x_{k}\cdot e^{{-2\ пи i}{\frac {mk}{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44406da8bf27ff396599d35e91d4328c3f961a81)
![{\displaystyle \varphi (n)={\mathcal {F}}\{\mathbf {x} \}[1]=\sum \limits _{k=1}^{n}\gcd(k,n) e^{-2\pi i{\frac {k}{n}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a88a09856ce4f73559b80fb01e44bdd70af8309)












![{\displaystyle {\begin{aligned}\varphi (20)&=\mu (1)\cdot 20+\mu (2)\cdot 10+\mu (4)\cdot 5+\mu (5)\cdot 4+\mu (10)\cdot 2+\mu (20)\cdot 1\\[.5em]&=1\cdot 20-1\cdot 10+0\cdot 5-1\cdot 4+1\cdot 2+0\cdot 1=8.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a4ce2d54734e410d4eea1d1a6b0d62ad7fbfed9)




































![{\displaystyle {\begin{aligned}\lim \inf {\frac {\varphi (n+1)}{\varphi (n)}}&=0\quad {\text{and}}\\[5px] \lim \sup {\frac {\varphi (n+1)}{\varphi (n)}}&=\infty .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc005e44784aa197220263d20f9a495ee655b528)




