Радиус Земли
| Радиус Земли | |
|---|---|
 Экваториальный ( а ), полярный ( б ) и средний арифметический радиусы Земли, определенные в редакции Всемирной геодезической системы 1984 года (не в масштабе) | |
Другие имена | земной радиус |
Общие символы | Р 🜨 , Р Е , а , б , а Е , б Е , Р е Е , Р п Е |
| единица СИ | метры |
| В базовых единицах СИ | м |
Поведение под преобразование координат | скаляр |
| Измерение | |
| Ценить | Экваториальный радиус : a = ( 6 378 , 1370 км ) Полярный радиус : b = ( 6 356,7523 км ) |
| Номинальный радиус Земли | |
|---|---|
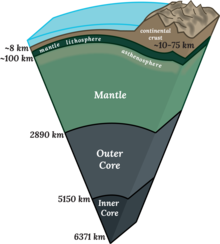 Разрез недр Земли | |
| Общая информация | |
| Система единиц | астрономия , геофизика |
| Единица | расстояние |
| Символ | , , |
| Конверсии | |
| 1 в ... | ... равно... |
| Базы СИ объединены | 6.3781 × 10 6 м [ 1 ] |
| Метрическая система | От 6357 до 6378 км |
| Английские единицы | От 3950 до 3963 миль |
| Геодезия |
|---|
 |
Радиус Земли (обозначается как R 🜨 или R E ) — это расстояние от центра Земли до точки на ее поверхности или вблизи нее. При аппроксимации фигуры Земли ( земным сфероидом сплюснутым эллипсоидом ) радиус варьируется от максимума ( экваториальный радиус , обозначенный a ) почти 6378 км (3963 мили) до минимума ( полярный радиус , обозначенный b ) почти 6357 км. (3950 миль).
Среднее глобальное значение обычно считается равным 6371 километру (3959 миль) с изменчивостью 0,3% (± 10 км) по следующим причинам. Международный союз геодезии и геофизики (IUGG) предоставляет три эталонных значения: средний радиус ( R 1 ) трех радиусов, измеренных в двух точках экватора и на полюсе; аутальный радиус , который представляет собой радиус сферы с той же площадью поверхности ( R 2 ); и объемный радиус , который представляет собой радиус сферы, имеющей тот же объем, что и эллипсоид ( R 3 ). [ 2 ] Все три значения составляют около 6371 километра (3959 миль).
сфероида Другие способы определения и измерения радиуса Земли включают либо радиус кривизны , либо фактическую топографию . Некоторые определения дают значения, выходящие за пределы диапазона между полярным радиусом и экваториальным радиусом, поскольку они учитывают локализованные эффекты.
Номинальный радиус Земли (обозначается ) иногда используется как единица измерения в астрономии и геофизике , коэффициент преобразования , используемый при выражении свойств планет как кратных или долей постоянного земного радиуса; если выбор между экваториальным или полярным радиусом не очевиден, следует принять экваториальный радиус, как рекомендовано Международным астрономическим союзом (МАС). [ 1 ]
Введение
[ редактировать ]
Вращение Земли , изменения внутренней плотности и внешние приливные силы заставляют ее форму систематически отклоняться от идеальной сферы. [ а ] Локальная топография увеличивает дисперсию, в результате чего поверхность становится очень сложной. Чтобы быть понятными, наши описания поверхности Земли должны быть проще реальности. Следовательно, мы создаем модели, аппроксимирующие характеристики поверхности Земли, обычно полагаясь на самую простую модель, соответствующую потребностям.
Каждая из широко используемых моделей включает в себя некоторое понятие геометрического радиуса . Строго говоря, сферы — единственные твердые тела, имеющие радиусы, но более широкое использование термина «радиус» распространено во многих областях, в том числе в тех, которые имеют дело с моделями Земли. Ниже приводится неполный список моделей поверхности Земли, упорядоченный от точных к более приблизительным:
- Реальная поверхность Земли
- Геоид . , определяемый средним уровнем моря в каждой точке реальной поверхности [ б ]
- Сфероид для моделирования всей , также называемый эллипсоидом вращения, геоцентрический Земли или геодезический для региональных работ. [ с ]
- Сфера
В случае геоида и эллипсоидов фиксированное расстояние от любой точки модели до указанного центра называется «радиусом Земли» или «радиусом Земли в этой точке» . [ д ] также принято называть Любой средний радиус сферической модели «радиусом Земли» . С другой стороны, при рассмотрении реальной поверхности Земли редко упоминается «радиус», поскольку в этом обычно нет практической необходимости. Скорее, полезно возвышение над или ниже уровня моря.
Независимо от модели, любой из этих геоцентрических радиусов находится между полярным минимумом около 6357 км и экваториальным максимумом около 6378 км (от 3950 до 3963 миль). Следовательно, Земля отклоняется от идеальной сферы всего на треть процента, что подтверждает сферическую модель в большинстве контекстов и оправдывает термин «радиус Земли». Хотя конкретные значения различаются, концепции в этой статье распространяются на любую крупную планету .
Физика деформации Земли
[ редактировать ]Вращение планеты заставляет ее приближаться к сплюснутому эллипсоиду /сфероиду с выпуклостью на экваторе и уплощением на северном и южном полюсах , так что экваториальный радиус a больше полярного радиуса b примерно на aq . Константа сжатия q определяется выражением
где ω — угловая частота , G — гравитационная постоянная , а M — масса планеты. [ и ] Для Земли 1 / q ≈ 289 , что близко к измеренному обратному уплощению 1 / ж ≈ 298,257 . Кроме того, выпуклость на экваторе медленно меняется. Выпуклость уменьшалась, но с 1998 года выпуклость увеличилась, возможно, из-за перераспределения океанской массы посредством течений. [ 4 ]

Изменение плотности и толщины земной коры приводит к изменению силы тяжести по поверхности и во времени, так что средний уровень моря отличается от эллипсоида. Эта разница и есть геоида высота : положительная сверху или снаружи эллипсоида, отрицательная снизу или внутри. Изменение высоты геоида на Земле составляет менее 110 м (360 футов). Высота геоида может резко измениться из-за землетрясений (например, Суматра-Андаманское землетрясение ) или сокращения ледяных масс (например, в Гренландии ). [ 5 ]
Не все деформации возникают внутри Земли. Гравитационное притяжение Луны или Солнца может привести к изменению поверхности Земли в данной точке на десятые доли метра в течение почти 12-часового периода (см. Земной прилив ).
Радиус и местные условия
[ редактировать ]
Учитывая локальные и переходные воздействия на высоту поверхности, значения, определенные ниже, основаны на модели «общего назначения», уточненной настолько глобально, насколько это возможно, в пределах 5 м (16 футов) от высоты опорного эллипсоида и с точностью до 100 м (330 футов). среднего уровня моря (без учета высоты геоида).
Кроме того, радиус можно оценить по кривизне Земли в определенной точке. Как и у тора , кривизна в точке будет наибольшей (наибольшей) в одном направлении (север-юг на Земле) и наименьшей (самой плоской) перпендикулярно (восток-запад). Соответствующий радиус кривизны зависит от местоположения и направления измерения от этой точки. Следствием этого является то, что расстояние до истинного горизонта на экваторе немного короче в направлении север-юг, чем в направлении восток-запад.
Таким образом, местные различия в рельефе не позволяют определить единый «точный» радиус. Можно принять только идеализированную модель. Со времени оценки Эратосфена было создано множество моделей. Исторически эти модели основывались на региональной топографии, что давало наилучший опорный эллипсоид. [ сломанный якорь ] для обследуемой территории. По мере того, как спутниковое дистанционное зондирование и особенно система глобального позиционирования приобретали все большее значение, были разработаны настоящие глобальные модели, которые, хотя и не столь точны для региональных работ, но лучше всего приближают Землю в целом.
Экстремумы: экваториальный и полярный радиусы.
[ редактировать ]Следующие радиусы получены из Всемирной геодезической системы 1984 года ( WGS-84 ) опорного эллипсоида . [ 6 ] Это идеализированная поверхность, и земные измерения, используемые для ее расчета, имеют погрешность ± 2 м как в экваториальном, так и в полярном измерениях. [ 7 ] Дополнительные расхождения, вызванные топографическими различиями в конкретных местах, могут быть значительными. При определении положения наблюдаемого места использование более точных значений радиусов WGS-84 может не привести к соответствующему повышению точности . [ нужны разъяснения ]
Значение экваториального радиуса определяется с точностью до 0,1 м в WGS-84. Значение полярного радиуса в этом разделе округлено до ближайших 0,1 м, что, как ожидается, будет достаточным для большинства применений. Если требуется более точное значение его полярного радиуса, обратитесь к эллипсоиду WGS-84.
- Земли Экваториальный радиус а , или большая полуось , [ 8 ] : 11 — расстояние от его центра до экватора , равное 6378,1370 км (3963,1906 миль). [ 9 ] Экваториальный радиус часто используется для сравнения Земли с другими планетами .
- Земли Полярный радиус b или малая полуось [ 8 ] : 11 — расстояние от его центра до Северного и Южного полюсов, равное 6356,7523 км (3949,9028 миль).
Зависящие от местоположения радиусы
[ редактировать ]
Геоцентрический радиус
[ редактировать ]Геоцентрический радиус — это расстояние от центра Земли до точки на поверхности сфероида на геодезической широте φ , определяемое формулой: [ 10 ]
где a и b — соответственно экваториальный и полярный радиусы.
Экстремальные геоцентрические радиусы на эллипсоиде совпадают с экваториальным и полярным радиусами. Они являются вершинами эллипса и также совпадают с минимальным и максимальным радиусом кривизны.
Радиусы кривизны
[ редактировать ]Главные радиусы кривизны
[ редактировать ]Различают два основных радиуса кривизны : по меридиональному и нормальному вертикальным сечениям .
Меридиональный
[ редактировать ]В частности, Земли меридиональный радиус кривизны (в направлении север-юг) в точке φ составляет: [ 11 ]
где это эксцентриситет Земли. Это радиус, который Эратосфен измерил при измерении дуги .
Прайм вертикальный
[ редактировать ]
Если одна точка появилась восточнее другой, можно найти приблизительную кривизну в направлении восток-запад. [ ж ]
Первичный Земли вертикальный радиус кривизны , также называемый поперечным радиусом кривизны Земли , определяется перпендикулярно ( ортогонально ) к M на геодезической широте φ. [ г ] и это: [ 11 ]
N также можно интерпретировать геометрически как нормальное расстояние от поверхности эллипсоида до полярной оси. [ 12 ] Радиус параллели широты определяется выражением . [ 13 ] [ 14 ]
Полярный и экваториальный радиус кривизны
[ редактировать ]равен Меридиональный радиус кривизны Земли на экваторе меридиана полурасширенной прямой кишке :
- М е = b 2 / а = 6335,439 км
равен Первичный вертикальный радиус кривизны Земли на экваторе экваториальному радиусу N e = a .
( Полярный радиус кривизны Земли меридиональный или вертикальный) равен:
- М п = Н п = a 2 / б = 6399,594 км
Вывод
[ редактировать ]Расширенный контент
|
|---|
Комбинированные радиусы кривизны
[ редактировать ]Азимутальный
[ редактировать ]Земли Азимутальный радиус кривизны вдоль нормального сечения Земли по азимуту (измеренному по часовой стрелке от севера) α и на широте φ выводится из формулы кривизны Эйлера следующим образом: [ 16 ] : 97
Ненаправленный
[ редактировать ]Можно объединить указанные выше главные радиусы кривизны ненаправленным образом.
Земли Гауссов радиус кривизны на широте φ равен: [ 16 ]
Где K — гауссова кривизна , .
Средний Земли радиус кривизны на широте φ равен: [ 16 ] : 97
Глобальное радио
[ редактировать ]Землю можно смоделировать как сферу разными способами. В этом разделе описаны распространенные способы. Для различных радиусов, полученных здесь, используются обозначения и размеры, отмеченные выше для Земли, полученные на основе эллипсоида WGS-84 ; [ 6 ] а именно,
- Экваториальный радиус : a = ( 6 378 , 1370 км )
- Полярный радиус : b = ( 6 356,7523 км )
Поскольку сфера является грубой аппроксимацией сфероида, который сам по себе является аппроксимацией геоида, единицы измерения здесь даны в километрах, а не в миллиметрах, подходящих для геодезии.
Среднеарифметический радиус
[ редактировать ]
В геофизике Международный союз геодезии и геофизики (IUGG) определяет Земли средний арифметический радиус (обозначается R 1 ) как [ 2 ]
Коэффициент два объясняет двухосную симметрию земного сфероида, разновидности трехосного эллипсоида. Для Земли средний арифметический радиус составляет 6371,0088 км (3958,7613 миль). [ 17 ]
Аутентичный радиус
[ редактировать ]Аутентичный радиус Земли (что означает «равная площадь» ) — это радиус гипотетической идеальной сферы, имеющей ту же площадь поверхности, что и опорный эллипсоид . IUGG обозначает аутентичный радиус как R 2 . [ 2 ] Для сфероида существует решение в замкнутой форме: [ 8 ]
где е 2 = a 2 − б 2 / а 2 и A — площадь поверхности сфероида.
Для Земли аутентичный радиус составляет 6371,0072 км (3958,7603 мили). [ 17 ]
Аутентичный радиус также соответствует радиусу (глобальной) средней кривизны , полученному усреднением гауссовой кривизны, , над поверхностью эллипсоида. Используя теорему Гаусса – Бонне , это дает
Объемный радиус
[ редактировать ]Другая сферическая модель определяется объёмным радиусом Земли , который представляет собой радиус сферы объёма, равного эллипсоиду. IUGG R обозначает объемный радиус 3 как . [ 2 ]
Для Земли объемный радиус равен 6371,0008 км (3958,7564 мили). [ 17 ]
Выпрямляющий радиус
[ редактировать ]Другой глобальный радиус — это выпрямляющий радиус Земли , дающий сферу с окружностью, равной периметру эллипса , описываемого любым полярным поперечным сечением эллипсоида. Для этого необходимо эллиптический интеграл найти , учитывая полярный и экваториальный радиусы:
Радиус выпрямления эквивалентен среднему меридиональному значению, которое определяется как среднее значение M : [ 8 ]
Для пределов интегрирования [0, π / 2 ], интегралы для выпрямления радиуса и среднего радиуса дают один и тот же результат, который для Земли составляет 6 367,4491 км (3 956,5494 миль).
Среднее меридиональное значение хорошо аппроксимируется полукубическим средним значением двух осей: [ нужна ссылка ]
что отличается от точного результата менее чем на 1 мкм (4 × 10 −5 в); среднее значение двух осей,
Также можно использовать около 6 367,445 км (3 956,547 миль).
Топографические радиусы
[ редактировать ]Приведенные выше математические выражения применимы к поверхности эллипсоида. Земли В приведенных ниже случаях рассматривается топография выше или ниже эталонного эллипсоида . По сути, это топографические геоцентрические расстояния R t , которые зависят не только от широты.
Топографические крайности
[ редактировать ]- Максимальный R t : вершина Чимборасо находится на расстоянии 6384,4 км (3967,1 миль) от центра Земли.
- Минимальный R t : дно Северного Ледовитого океана находится на расстоянии 6352,8 км (3947,4 миль) от центра Земли. [ 18 ]
Топографическое глобальное среднее значение
[ редактировать ]Топографическое среднее геоцентрическое расстояние усредняет высоту повсюду, в результате чего значение на 230 м превышает средний радиус IUGG , аутентичный радиус или объемный радиус . Это топографическое среднее значение составляет 6 371,230 км (3 958,899 миль) с погрешностью 10 м (33 фута). [ 19 ]
Производные величины: диаметр, окружность, длина дуги, площадь, объем.
[ редактировать ]Земли Диаметр просто в два раза больше радиуса Земли; например, экваториальный диаметр (2a ) и полярный диаметр (2b ) . Для эллипсоида WGS84 это соответственно:
- 2 а = 12 756,2740 км (7 926,3812 миль) ,
- 2b = 12 713,5046 км (7,899,8055 миль) .
Окружность Земли равна длине периметра . Экваториальная окружность — это просто периметр круга : C e =2 πa , выраженный в экваториальном радиусе a . Полярная окружность равна C p =4 m p , что в четыре раза больше четверти меридиана m p = aE ( e ), куда полярный радиус b входит через эксцентриситет, e = (1− b 2 / а 2 ) 0.5 ; см . в разделе «Эллипс#Окружность» подробности .
Длина дуги более общих кривых поверхности , таких как дуги меридианов и геодезические , также может быть получена из экваториальных и полярных радиусов Земли.
Аналогично и для площади поверхности , либо на основе картографической проекции , либо на основе геодезического многоугольника .
Объем Земли или объем опорного эллипсоида равен V = 4 / 3 π a 2 б . Используя параметры WGS84 эллипсоида вращения , a = 6378,137 км b = км . × V , и = 1,08321 6356,7523142 10 12 км 3 (2.5988 × 10 11 с ми) . [ 20 ]
Номинальные радиусы
[ редактировать ]В астрономии Международный астрономический союз обозначает номинальный экваториальный радиус Земли как , что составляет ровно 6378,1 км (3963,2 мили). [ 1 ] : 3 Номинальный полярный радиус Земли определяется точно как = 6356,8 км (3949,9 миль). Эти значения соответствуют конвенции нулевого прилива Земли . Экваториальный радиус обычно используется в качестве номинального значения, если явно не требуется полярный радиус. [ 1 ] : 4 Номинальный радиус служит единицей длины в астрономии . (Обозначения определены так, что их можно легко обобщить для других планет ; например, для номинального радиуса полярного Юпитера .)
Опубликованные значения
[ редактировать ]В этой таблице суммированы принятые значения радиуса Земли.
| Агентство | Описание | Стоимость (в метрах) | Ссылка |
|---|---|---|---|
| НУ ДАВАЙ ЖЕ | номинальный экваториальный «нулевой прилив» | 6 378 100 | [ 1 ] |
| НУ ДАВАЙ ЖЕ | номинальный полярный «нулевой прилив» | 6 356 800 | [ 1 ] |
| IUGG | экваториальный радиус | 6 378 137 | [ 2 ] |
| IUGG | малая полуось ( б ) | 6 356 752 .3141 | [ 2 ] |
| IUGG | полярный радиус кривизны ( c ) | 6 399 593 .6259 | [ 2 ] |
| IUGG | средний радиус ( R 1 ) | 6 371 008 .7714 | [ 2 ] |
| IUGG | радиус сферы той же поверхности ( R 2 ) | 6 371 007 .1810 | [ 2 ] |
| IUGG | радиус сферы того же объема ( R 3 ) | 6 371 000 .7900 | [ 2 ] |
| что | Эллипсоид WGS-84 , большая полуось ( а ) | 6 378 137 .0 | [ 6 ] |
| что | Эллипсоид WGS-84, малая полуось ( б ) | 6 356 752 .3142 | [ 6 ] |
| что | Эллипсоид WGS-84, полярный радиус кривизны ( в ) | 6 399 593 .6258 | [ 6 ] |
| что | Эллипсоид WGS-84, Средний радиус полуосей ( R 1 ) | 6 371 008 .7714 | [ 6 ] |
| что | Эллипсоид WGS-84, радиус равновеликой сферы ( R 2 ) | 6 371 007 .1809 | [ 6 ] |
| что | Эллипсоид WGS-84, радиус сферы равного объема ( R 3 ) | 6 371 000 .7900 | [ 6 ] |
| GRS 80 Большая полуось ( а ) | 6 378 137 .0 | ||
| GRS 80 Малая полуось ( б ) | ≈6 356 752 .314 140 | ||
| Сферическая Земля радиуса ( R E ) | 6 366 707 .0195 | [ 21 ] | |
| меридиональный радиус кривизны на экваторе | 6 335 439 | ||
| Максимум (вершина Чимборасо) | 6 384 400 | [ 18 ] | |
| Минимум (дно Северного Ледовитого океана) | 6 352 800 | [ 18 ] | |
| Среднее расстояние от центра до поверхности | 6 371 230 ± 10 | [ 19 ] |
История
[ редактировать ]Первое опубликованное упоминание о размерах Земли появилось около 350 г. до н.э. , когда Аристотель сообщил в своей книге «О небесах». [ 22 ] что математики предположили, что окружность Земли равна 400 000 стадий . Ученые интерпретировали фигуру Аристотеля как весьма точную. [ 23 ] почти вдвое превышает истинную стоимость. [ 24 ] Первое известное научное измерение и вычисление окружности Земли было выполнено Эратосфеном примерно в 240 г. до н. э. Оценки погрешности измерений Эратосфена колеблются от 0,5% до 17%. [ 25 ] И для Аристотеля, и для Эратосфена неуверенность в точности их оценок связана с современной неопределенностью, какую длину стадиона они имели в виду.
Около 100 г. до н.э. Посидоний Апамейский пересчитал радиус Земли и обнаружил, что он близок к радиусу Эратосфена. [ 26 ] но позже Страбон ошибочно приписал ему величину примерно в 3/4 от действительного размера. [ 27 ] Клавдий Птолемей около 150 г. н. э. предоставил эмпирические доказательства, подтверждающие сферическую форму Земли . [ 28 ] но он принял меньшую ценность, приписываемую Посидонию. Его весьма влиятельный труд « Альмагест » [ 29 ] не оставило у средневековых ученых сомнений в том, что Земля имеет сферическую форму, но они ошибались относительно ее размеров.
К 1490 году Христофор Колумб считал, что путешествие на 3000 миль на запад от западного побережья Пиренейского полуострова позволит ему достичь восточных побережий Азии . [ 30 ] Однако в 1492 году это путешествие привело его флот в Америку . Экспедиция Магеллана (1519–1522), ставшая первым кругосветным плаванием , убедительно продемонстрировала шарообразность Земли. [ 31 ] и подтвердил первоначальные измерения Эратосфена в 40 000 км (25 000 миль).
Около 1690 года Исаак Ньютон и Христиан Гюйгенс утверждали, что Земля ближе к сплюснутому сфероиду, чем к сфере. Однако около 1730 года Жак Кассини выступил за вытянутый сфероид вместо этого из-за различных интерпретаций ньютоновской механики . [ 32 ] Чтобы решить этот вопрос, Французская геодезическая миссия (1735–1739) измерила один градус широты в двух местах: одном возле Полярного круга , а другом около экватора . Экспедиция обнаружила, что гипотеза Ньютона верна: [ 33 ] Земля сплющена на полюсах вращения из-за центробежной силы .
См. также
[ редактировать ]Примечания
[ редактировать ]- ^ Подробности см. на рисунке Земли , геоида и земного прилива .
- ^ У геоида нет единого центра; оно варьируется в зависимости от местных геодезических условий.
- ^ В геоцентрическом эллипсоиде центр эллипсоида совпадает с некоторым вычисленным центром Земли и лучше всего моделирует Землю в целом. Геодезические эллипсоиды лучше соответствуют региональным особенностям геоида. Частичная поверхность эллипсоида подгоняется к области, и в этом случае центр и ориентация эллипсоида обычно не совпадают с центром масс или осью вращения Земли.
- ^ Значение радиуса полностью зависит от широты в случае модели эллипсоида и почти так же от геоида.
- ^ Это следует из Международного астрономического союза правила определения (2): планета принимает форму благодаря гидростатическому равновесию , когда гравитация и центробежные силы почти уравновешены. [ 3 ]
- ^ Направления восток-запад могут вводить в заблуждение. Точка B, которая кажется восточнее точки A, будет ближе к экватору, чем точка A. Таким образом, найденная таким образом кривизна меньше кривизны круга постоянной широты, за исключением экватора. В этой дискуссии Запад можно заменить на Восток.
- ^ N определяется как радиус кривизны в плоскости, которая нормальна как к поверхности эллипсоида, так и к меридиану, проходящему через конкретную интересующую точку.
Ссылки
[ редактировать ]- ^ Перейти обратно: а б с д и ж Мамаек, Э. Э; Прса, А; Торрес, Дж; и др. (2015). «Резолюция B3 МАС 2015 г. о рекомендуемых номинальных константах преобразования для выбранных солнечных и планетарных свойств». arXiv : 1510.07674 [ астро-ф.SR ].
- ^ Перейти обратно: а б с д и ж г час я дж Мориц, Х. (1980). Геодезическая справочная система, 1980 г. Архивировано 20 февраля 2016 г. в Wayback Machine по решению XVII Генеральной ассамблеи IUGG в Канберре.
- ^ Генеральная ассамблея IAU 2006: Результат голосования по резолюции IAU. Архивировано 7 ноября 2006 г. в Wayback Machine.
- ^ Спутники раскрывают тайну больших изменений в гравитационном поле Земли , 1 августа 2002 г., Центр космических полетов Годдарда .
- ^ Благодать НАСА обнаружила, что Гренландия тает быстрее, и «видит» землетрясение на Суматре [ постоянная мертвая ссылка ] , 20 декабря 2005 г., Центр космических полетов Годдарда .
- ^ Перейти обратно: а б с д и ж г час «Мировая геодезическая система Министерства обороны 1984 года: ее определение и взаимосвязь с местными геодезическими системами» . Проверено 17 октября 2018 г.
- ^ «Информация» (PDF) . земля-info.nga.mil . Архивировано из оригинала (PDF) 4 августа 2020 г. Проверено 31 декабря 2008 г.
- ^ Перейти обратно: а б с д Снайдер, JP (1987). Картографические проекции – Рабочее руководство (Профессиональный документ Геологической службы США 1395), стр. 16–17. Вашингтон, округ Колумбия: Типография правительства США.
- ^ «Экваториальный радиус Земли» . Численные стандарты фундаментальной астрономии: астрономические константы: текущие лучшие оценки (CBE) . Рабочая группа Отдела I IAU. 2012. Архивировано из оригинала 26 августа 2016 г. Проверено 10 августа 2016 г.
- ^ Мохиндер С. Гревал; Ангус П. Эндрюс; Крис Дж. Бартоне (2020). Глобальные навигационные спутниковые системы, инерциальная навигация и интеграция (4-е изд.). Джон Уайли и сыновья. п. 512. ИСБН 978-1-119-54783-9 .
- ^ Перейти обратно: а б Кристофер Джекели (2016). Геометрические системы отсчета в геодезии (PDF) . Университет штата Огайо, Колумбус, Огайо . Проверено 13 мая 2023 г.
- ^ Боуринг, Британская Колумбия (октябрь 1987 г.). «Заметки о кривизне в главном вертикальном сечении». Обзор опроса . 29 (226): 195–196. дои : 10.1179/sre.1987.29.226.195 .
- ^ Бомфорд, Г. (1952). Геодезия . Издательство Оксфордского университета.
- ^ Кристофер Джекели (2016). Геометрические системы отсчета в геодезии (PDF) . Университет штата Огайо, Колумбус, Огайо . Проверено 13 мая 2023 г.
- ^ Перейти обратно: а б с Девушка, Гарри (1950). Векторный и тензорный анализ . McGraw Hill Book Company, Inc., стр. 71–77 . ISBN 9780070365209 .
- ^ Перейти обратно: а б с Торге, Вольфганг (2001). Геодезия . ISBN 9783110170726 .
- ^ Перейти обратно: а б с Мориц, Х. (март 2000 г.). «Геодезическая справочная система 1980». Журнал геодезии . 74 (1): 128–133. Бибкод : 2000JGeod..74..128. . дои : 10.1007/s001900050278 . S2CID 195290884 .
- ^ Перейти обратно: а б с «Discover-TheWorld.com – Гуам – ДОСТОПРИМЕЧАТЕЛЬНОСТИ – Не пропустите – Марианская впадина» . Гуам.discover-theworld.com. 23 января 1960 г. Архивировано из оригинала 10 сентября 2012 г. Проверено 16 сентября 2013 г.
- ^ Перейти обратно: а б Фредерик Шамба; Бернар Валетт (2001). «Средний радиус, масса и инерция для эталонных моделей Земли» (PDF) . Физика Земли и недр планет . 124 (3–4): 234–253. Бибкод : 2001PEPI..124..237C . дои : 10.1016/S0031-9201(01)00200-X . Архивировано из оригинала (PDF) 30 июля 2020 года . Проверено 18 ноября 2017 г.
- ^ Уильямс, Дэвид Р. (1 сентября 2004 г.), Информационный бюллетень о Земле , НАСА , получено 17 марта 2007 г.
- ^ Филлипс, Уоррен (2004). Механика полета . John Wiley & Sons, Inc. с. 923. ИСБН 0471334588 .
- ^ Аристотель . На Небесах . Том. Книга II 298 Б. Проверено 5 ноября 2017 г.
- ^ Драммонд, Уильям (1817). «О науке египтян и халдеев, часть I». Классический журнал . 16 : 159.
- ^ Кларк, Александр Росс ; Гельмерт, Фридрих Роберт (1911). . В Чисхолме, Хью (ред.). Британская энциклопедия . Том. 8 (11-е изд.). Издательство Кембриджского университета. стр. 801–813.
- ^ «Эратосфен, греческий учёный» . Britannica.com . 2016.
- ↑ Посидоний, фрагмент 202.
- ^ Клеомед ( во фрагменте 202 ) заявил, что если расстояние измеряется каким-то другим числом, результат будет другим, и использование 3750 вместо 5000 дает следующую оценку: 3750 x 48 = 180 000; см. Фишер И., (1975), Другой взгляд на определения Эратосфеном и Посидонием окружности Земли , Ql. Дж. из Королевского Астрона. Соц., Том. 16, с. 152.
- ^ Терстон, Хью (1994). Ранняя астрономия . Нью-Йорк: Springer-Verlag Нью-Йорк. п. 138. ИСБН 0-387-94107-Х .
- ^ «Альмагест – Птолемей (Елизавета)» . project.iq.harvard.edu . Проверено 5 ноября 2022 г.
- ^ Джон Фрили , До Галилея: рождение современной науки в средневековой Европе (2013), ISBN 978-1468308501
- ^ Нэнси Смайлер Левинсон (2001). Магеллан и первое кругосветное путешествие . Хоутон Миффлин Харкорт. ISBN 978-0-395-98773-5 . Проверено 31 июля 2010 г.
- ^ Кассини, Жак (1738). Метод определения шарообразности Земли или нет (на французском языке). Архивировано из оригинала 27 января 2018 г. Проверено 9 февраля 2023 г.
- ^ Леваллуа, Жан-Жак (1986). «Жизнь наук» . Галлика . стр. 277–284, 288 . Проверено 22 мая 2019 г.
Внешние ссылки
[ редактировать ]- Меррифилд, Майкл Р. (2010). " Радиус Земли (и экзопланеты)» . Шестьдесят символов . Брэйди Харан для Ноттингемского университета .















![{\displaystyle A=a_{ij}=\sum _{\nu }{\frac {\partial r^{\nu }}{\partial w^{i}}}{\frac {\partial r^{\nu }}{\partial w^{j}}}=\left[{\begin{array}{ll}E&F\\F&G\end{array}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/610ddc59d9c8fd1c855d652056554a52ba34f54c)
![{\displaystyle r=[r^{1},r^{2},r^{3}]^{T}=[x,y,z]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7bbe1c37804b95a79f311e99dcbe998b2d2e9a08)



![{\displaystyle B=b_{ij}=\sum _{\nu }n^{\nu }{\frac {\partial ^{2}r^{\nu }}{\partial w^{i}\partial w^{j}}}=\left[{\begin{array}{ll}e&f\\f&g\end{array}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbf2608ffb7c50849beb59f181bd23f5710fd8c8)




















![{\displaystyle R_{3}={\sqrt[{3}]{a^{2}b}}\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef606031ae7a1ba9f55d4d71b5926c79968a0aac)





